Similar presentations:
Решение простейших тригонометрических уравнений
1. Решение простейших тригонометрических уравнений
2.
Цели урока :Повторить формулы для решения
простейших тригонометрических
уравнений.
Закрепить навык решения
тригонометрических уравнений.
Развитие умения анализировать,
обобщать, работать в группах.
3. ТРИГОНОМЕТРИЯ
4.
Тригономе́трия (от др.-греч. измерение треугольников) —раздел математики, в котором изучаются тригонометрические
функции и их использование в геометрии.
Данный термин впервые
появился в 1595 г. как
название книги немецкого
математика
Б.Питискуса (1561—1613), а
сама наука ещё в глубокой
древности использовалась
для расчётов в астрономии,
архитектуре
и геодезии (науке,
исследующей размеры и
форму Земли).
5.
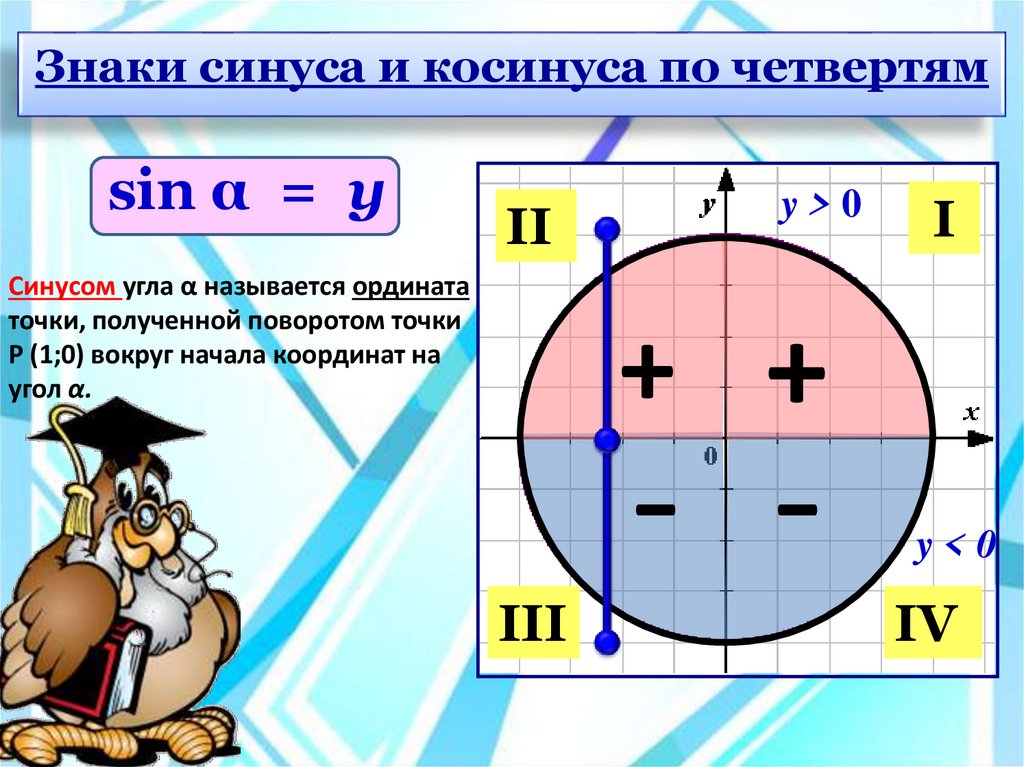
Знаки синуса и косинуса по четвертямsin α = у
II
Синусом угла α называется ордината
точки, полученной поворотом точки
Р (1;0) вокруг начала координат на
угол α.
y>0
I
+ +
- -
III
y<0
IV
6.
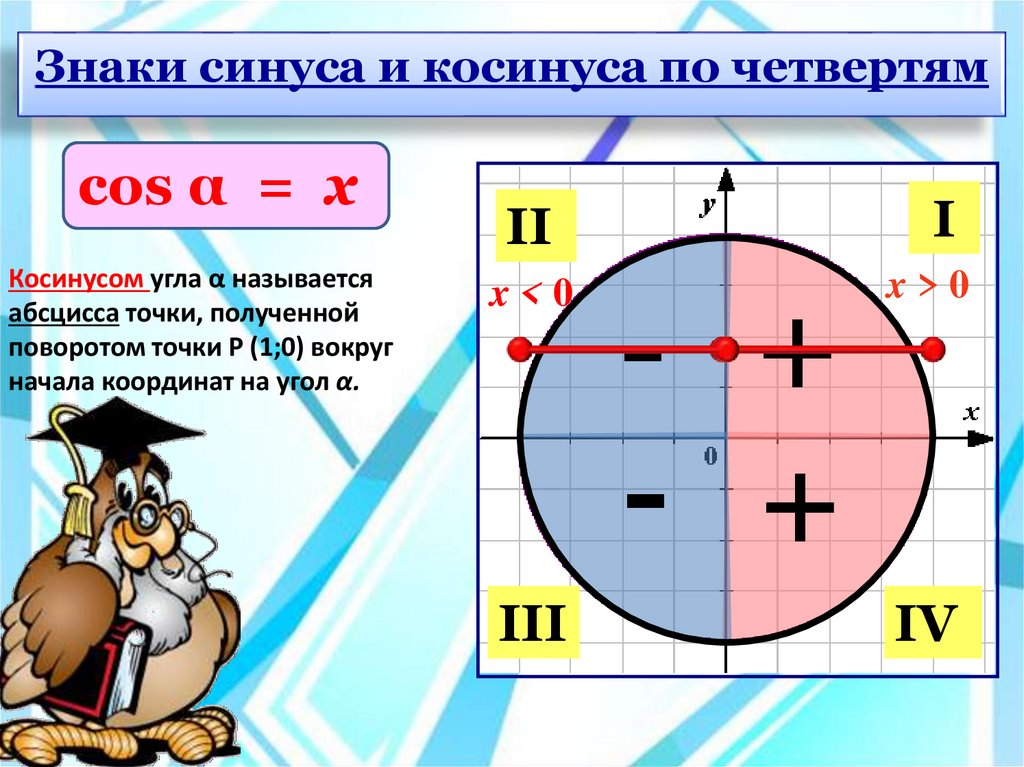
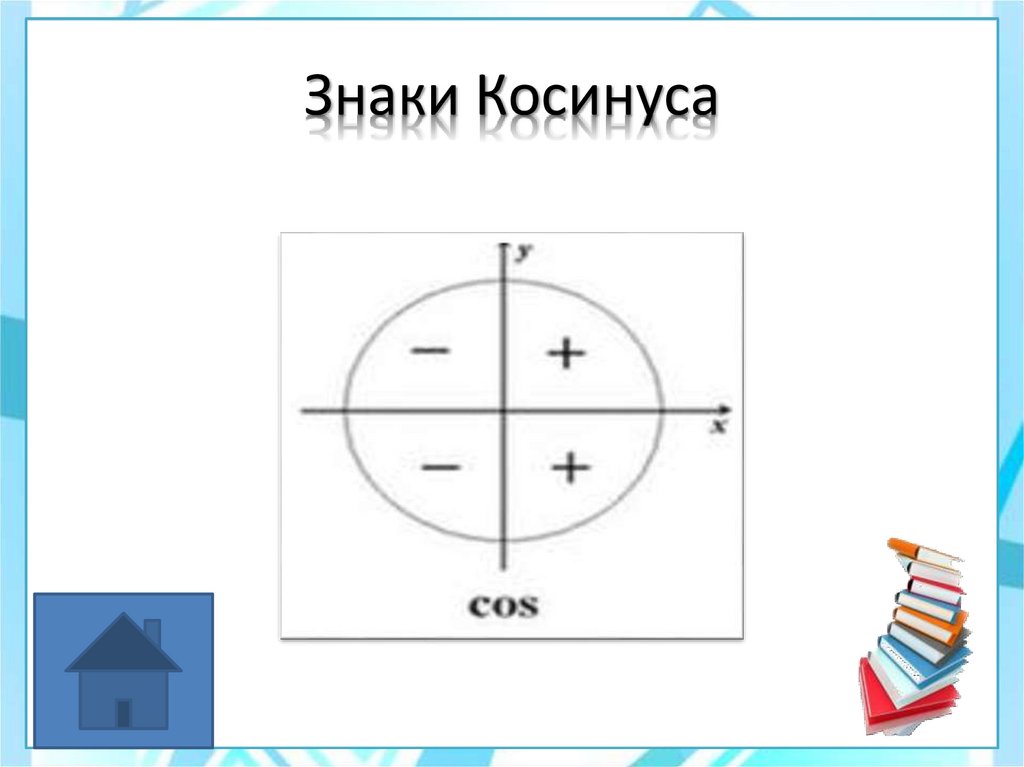
Знаки синуса и косинуса по четвертямcos α = x
Косинусом угла α называется
абсцисса точки, полученной
поворотом точки Р (1;0) вокруг
начала координат на угол α.
I
II
x<0
III
- +
- +
x>0
IV
7.
Тангенсом угла α называется отношение синуса угла α к егокосинусу.
tg
sin
cos
Котангенс угла α – это отношение косинуса угла α к его
синусу.
cos
ctg
sin
8.
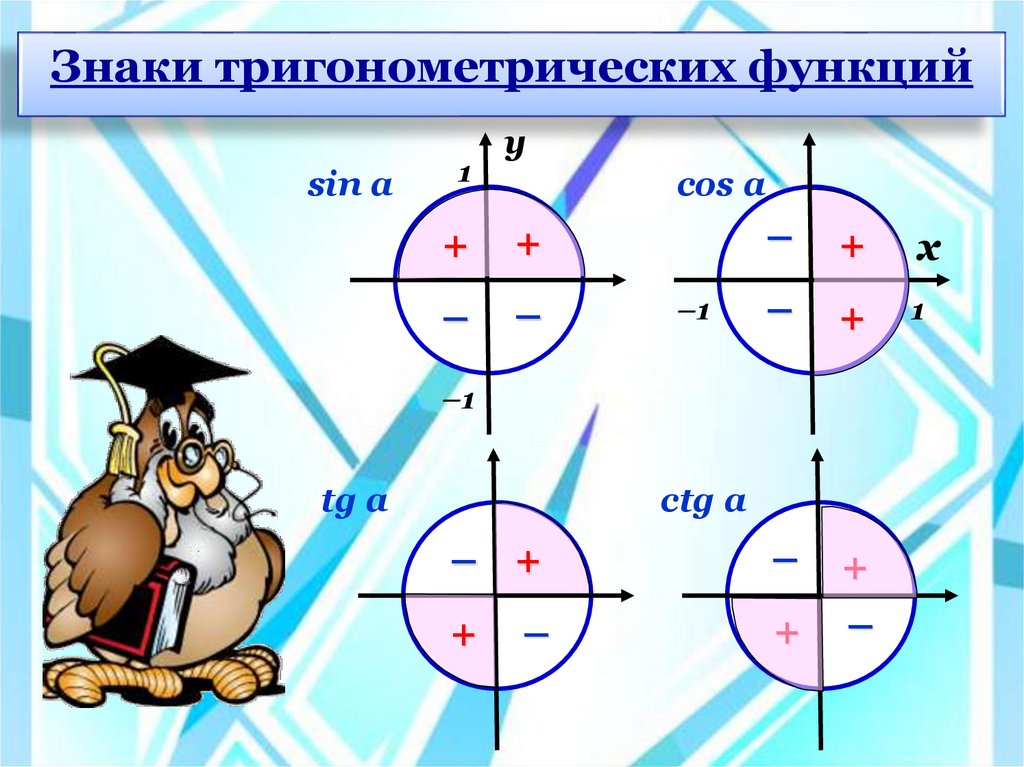
Знаки тригонометрических функцийsin a
1
y
cos a
+
+
–
–
–1
–
+
x
–
+
1
–1
tg a
ctg a
– +
+
–
–
+
+ –
9.
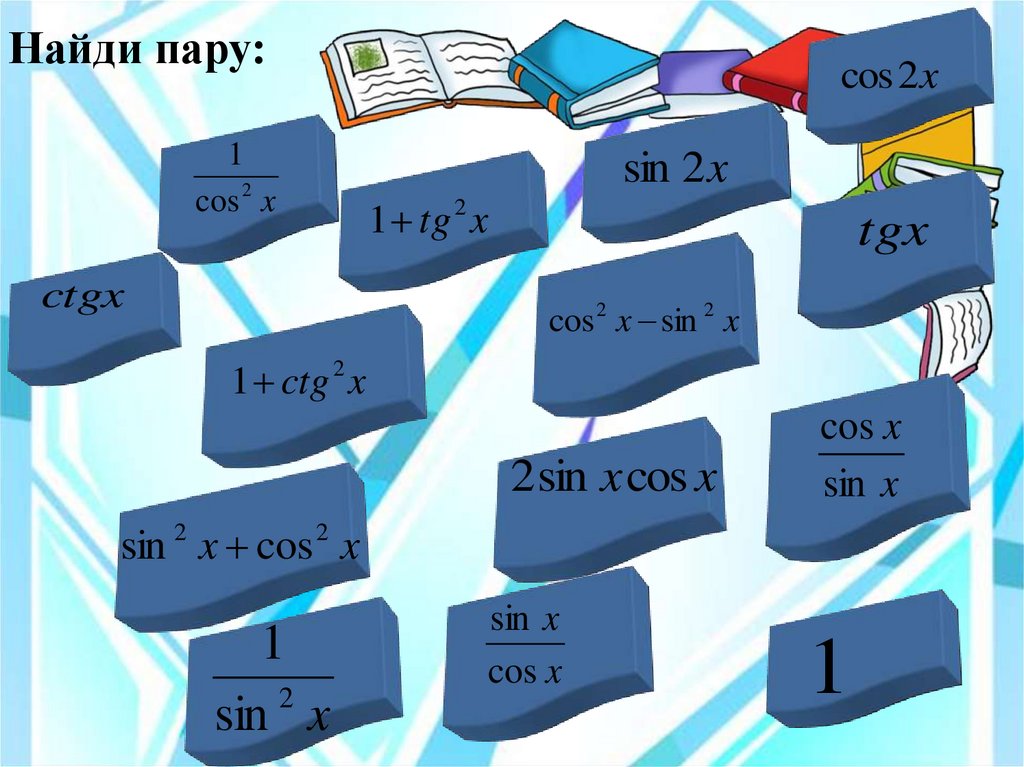
Найди пару:cos 2x
1
cos 2 x
sin 2 x
2
1 tg x
ctgx
tgx
cos 2 x sin 2 x
1 ctg 2 x
2 sin xcos x
cos x
sin x
sin x cos x
2
2
1
2
sin x
sin x
cos x
1
10. Решение простейших тригонометрических уравнений
ЕслиЕсли
Если
Если
уравнение не имеет решения.
уравнение не имеет решения.
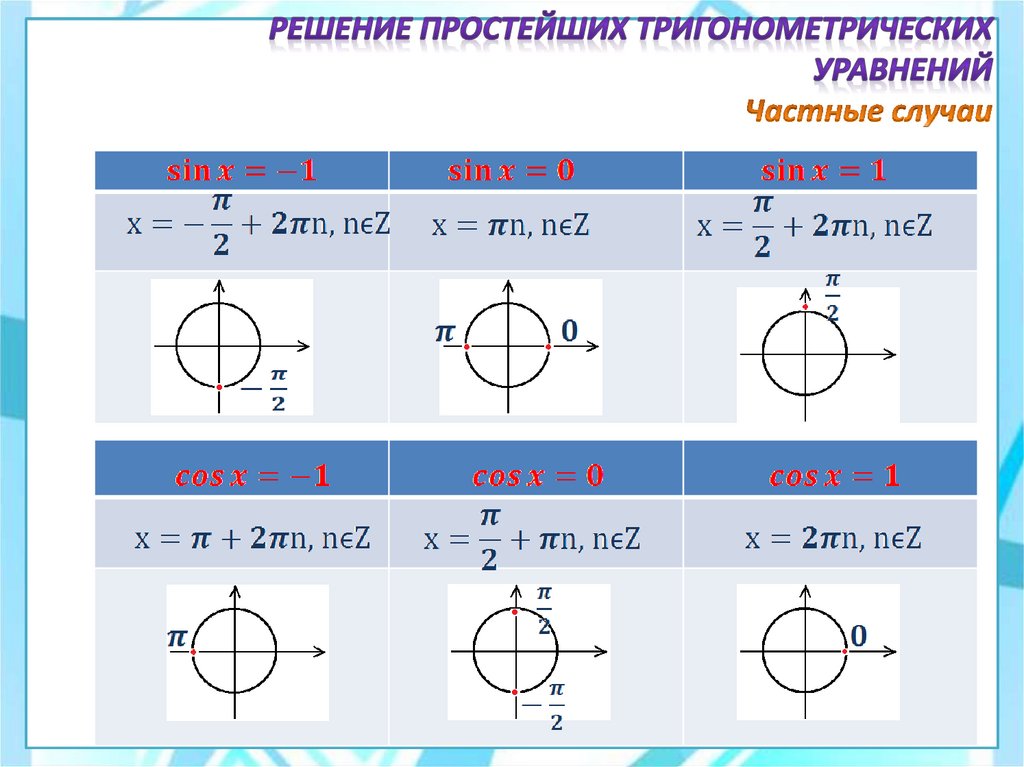
11. Решение простейших тригонометрических уравнений Частные случаи
12.
arcsin (-a) = - arcsin aarccos (-a) = П - arcsin a
arctg (-a) = - arctg a
13.
Какие из данных уравнений не имеют корней?а)sinx = -0,44
а)cosx = -0,33
б)cosx = 55
б)sinx = 4
в)ctgx = -8
в)tgx = -10
г)ctgx = 00
г)tgx = 0
14. Работа в группах
«С тригонометриейна ты…»
15.
«Примерыучат больше,
чем теория»
М .В. Ломоносов
16. МАТЕМАТИЧЕСКАЯ ИГРА
Правила:• Каждый играет за себя и за команду
• За правильно решенное задание
команда получает баллы
• Задания выбирают по очереди
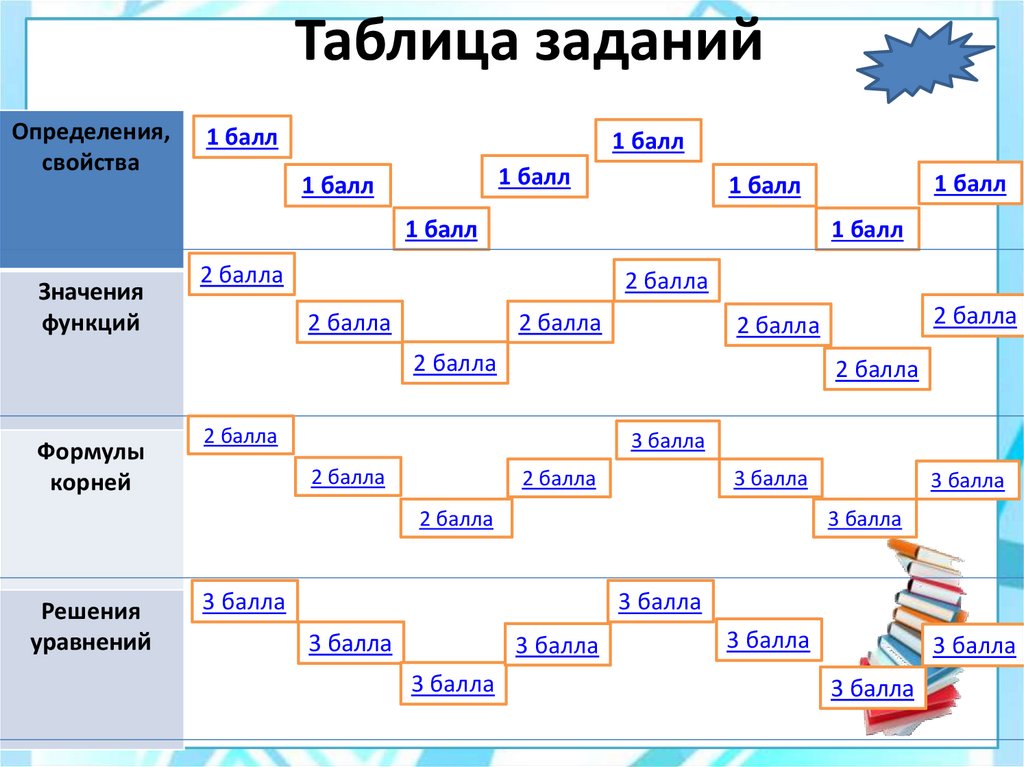
17. Таблица заданий
Определения,свойства
1 балл
1 балл
1 балл
1 балл
1 балл
Значения
функций
1 балл
2 балла
2 балла
2 балла
2 балла
2 балла
2 балла
3 балла
2 балла
2 балла
3 балла
2 балла
Решения
уравнений
2 балла
2 балла
2 балла
Формулы
корней
1 балл
1 балл
3 балла
3 балла
3 балла
3 балла
3 балла
3 балла
3 балла
3 балла
3 балла
3 балла
18. Ордината точки единичной окружности
–Синуса (sin)Ордината точки
единичной окружности
19. абсцисса точки единичной окружности
Косинуса (cos)абсцисса точки единичной
окружности
20. Это отношение синуса к косинусу
Тангенса (tg)Это отношение синуса
к косинусу
21. Это отношение косинуса к синусу
Котангенса (ctg)Это
отношение
косинуса к
синусу
22.
• Основноетригонометрическое
тождество
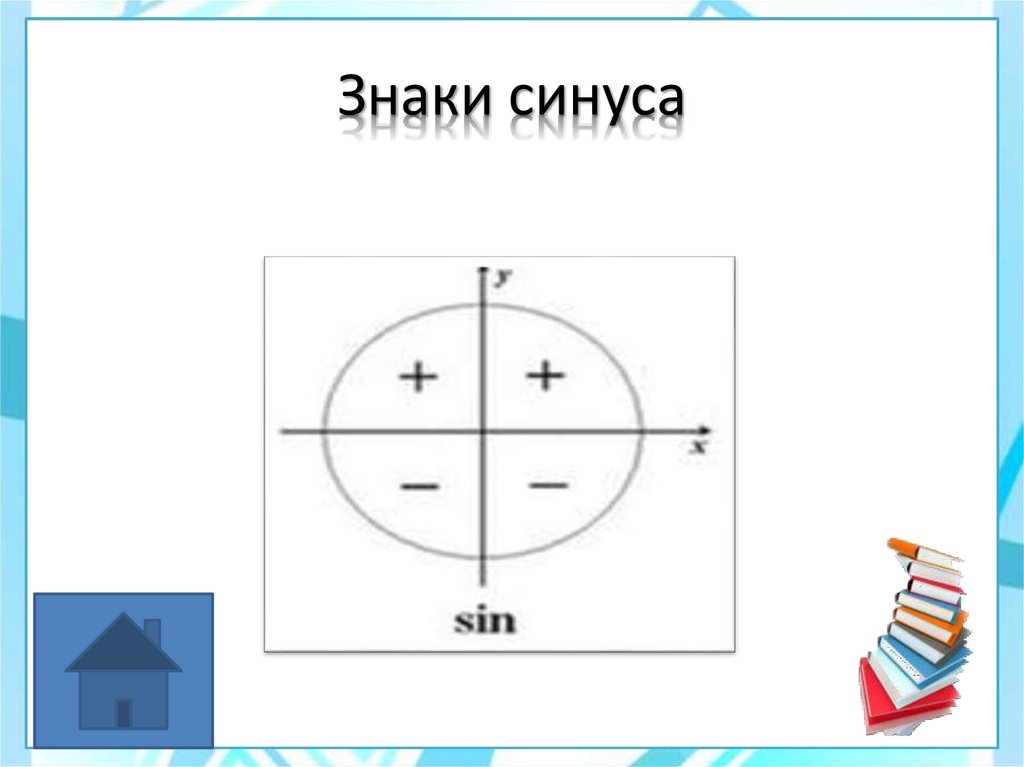
23. Знаки синуса
24. Знаки Косинуса
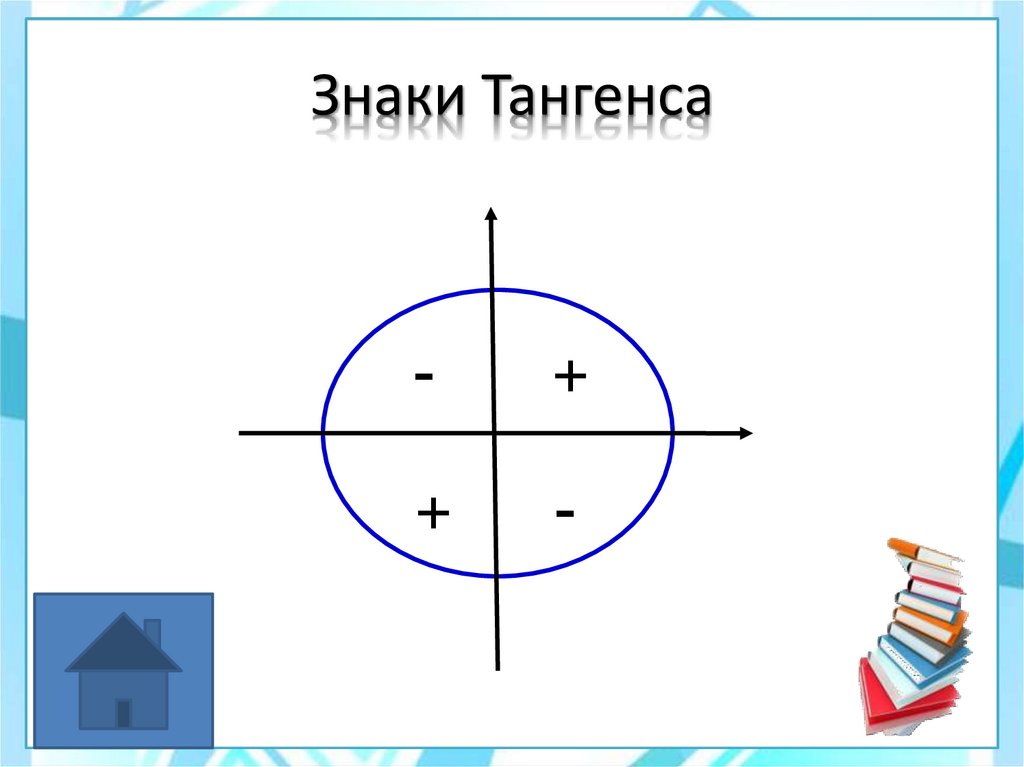
25. Знаки Тангенса
-+
+
-
26.
sin4
27.
sin6
28.
sin3
29.
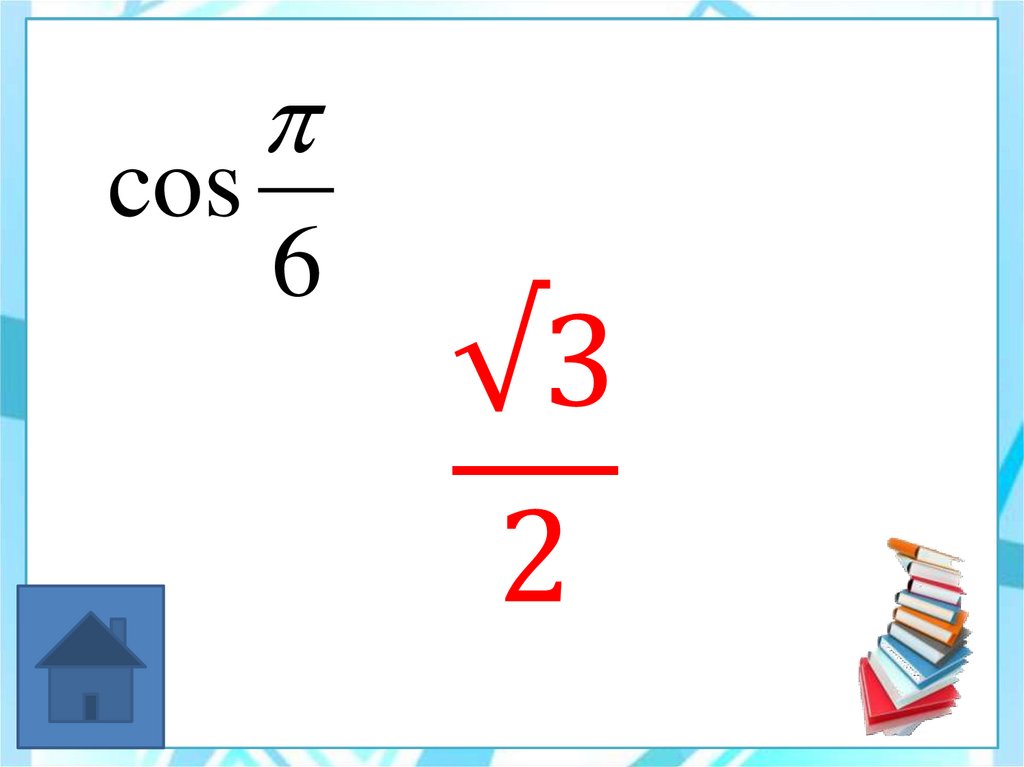
cos6
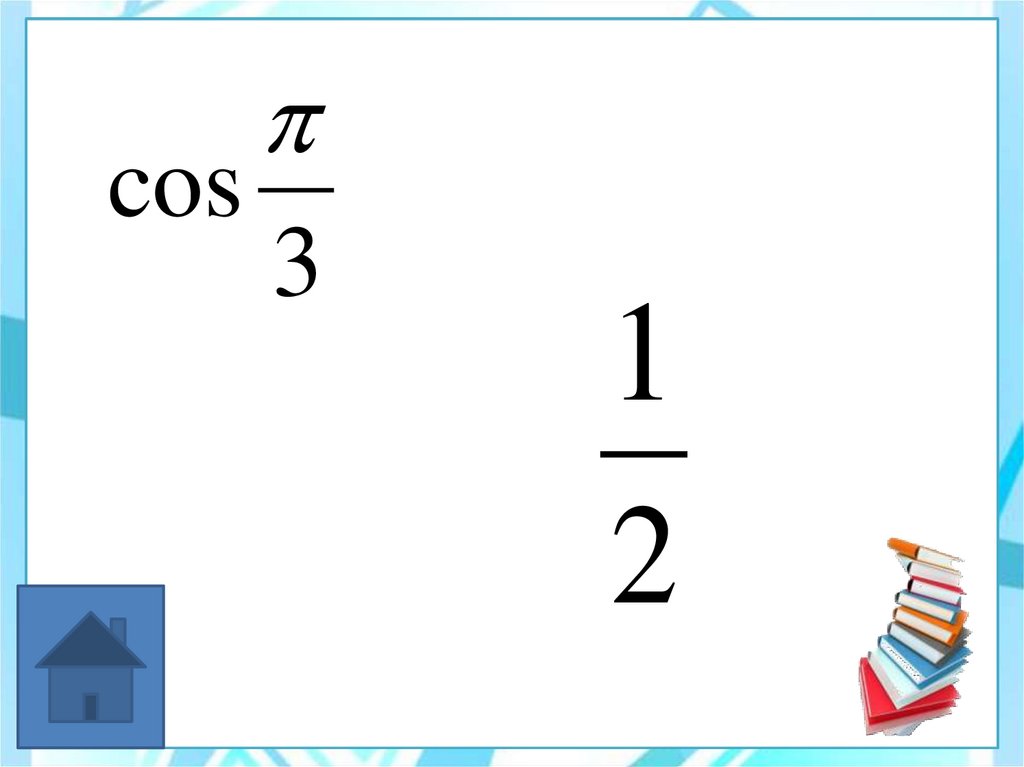
30.
cos3
1
2
31.
tg6
32.
tg3
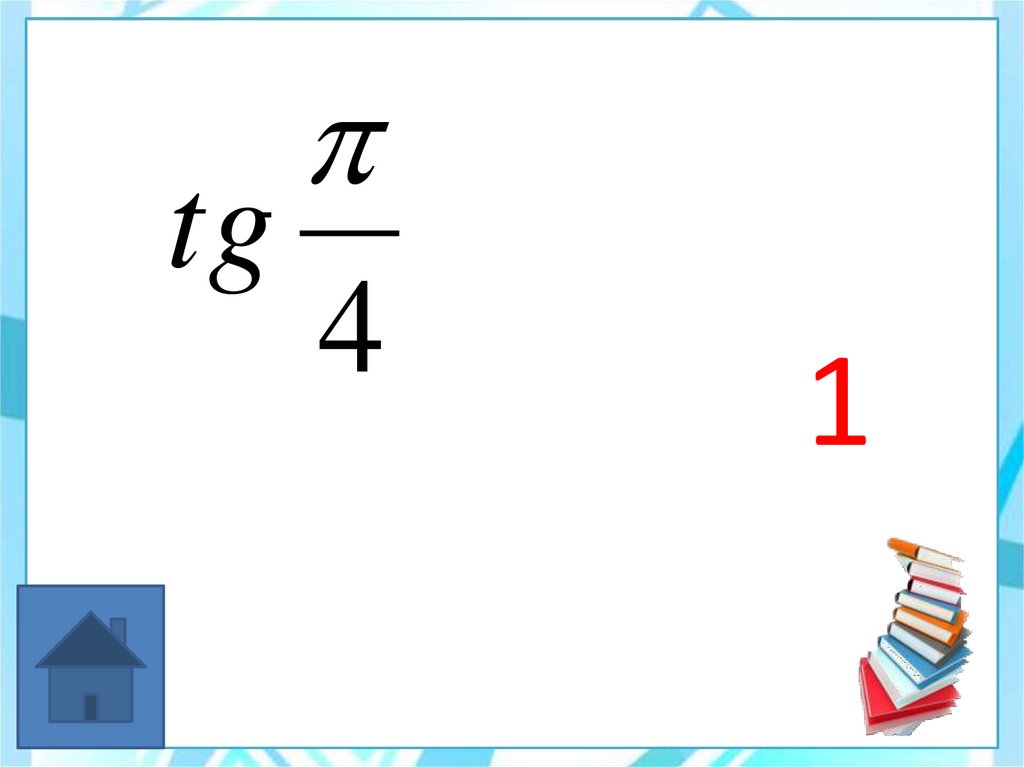
33. 1
tg4
1
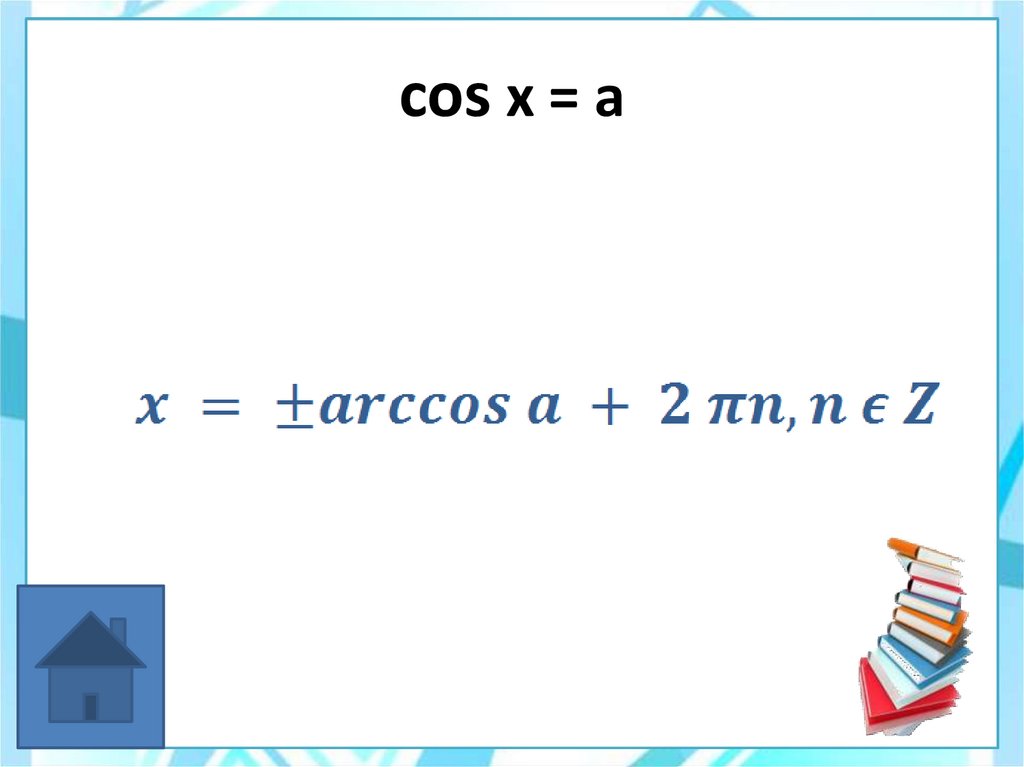
34. cos x = a
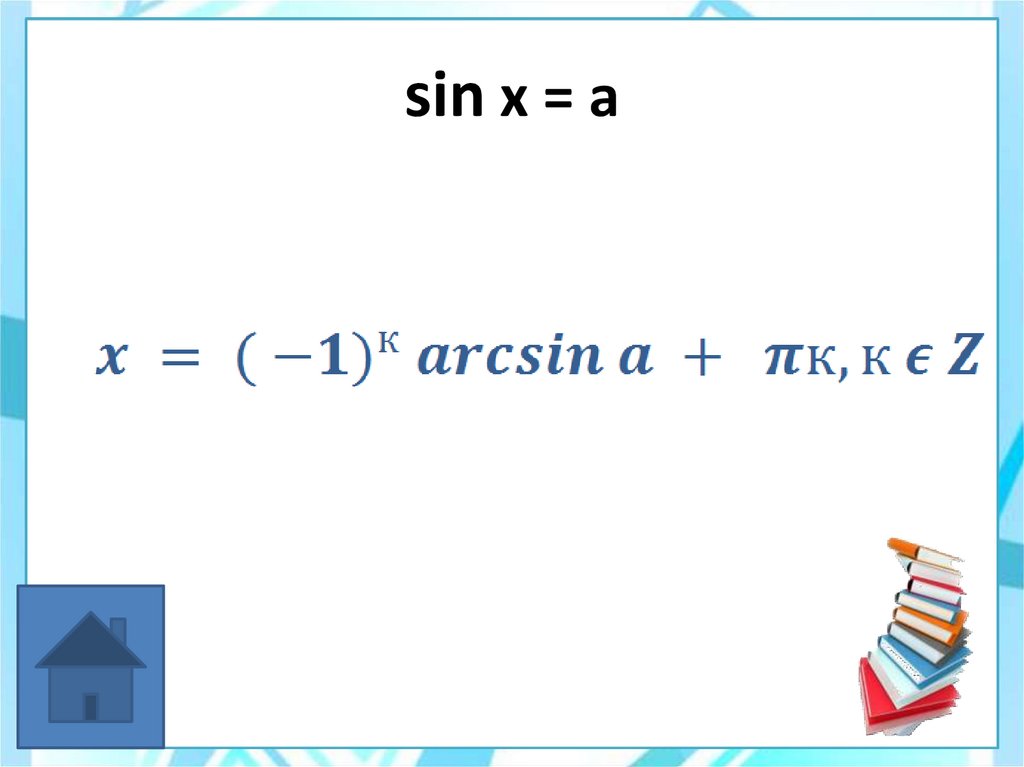
35. sin x = a
36. tg x = a
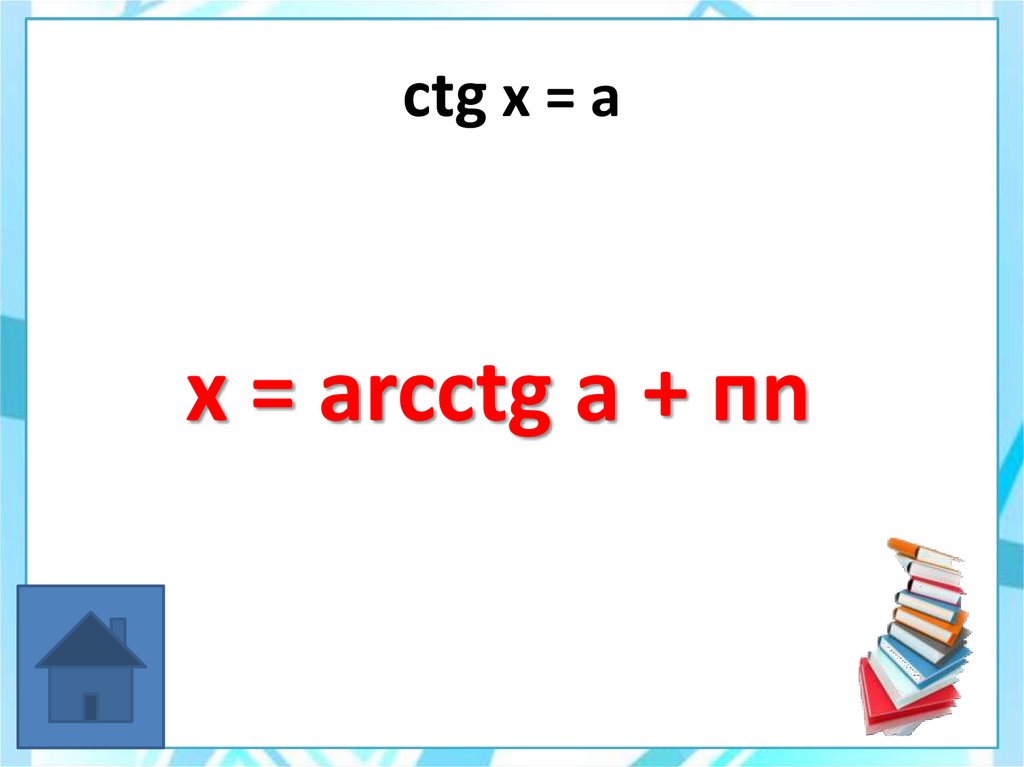
37. ctg x = a
x = arcctg a + пn38.
sin x = - ax=
n+1
(-1) arcsin
a + Пn
39. cos x = - a
x = ±(п-arccos a) +2 пn40. tg x = - a
x = - arctg a + пn41.
аrccos (-a) == П – arccos a
42. sin x= 0
x = пn, n принадлежит Z43. sin x = 1
x2
2 Пn, n z
44. sin x = -1
x2
2 Пn, n z
45. cos x = 0
x2
Пn, n z
46. cos x = 1
x 2 Пn, n z47. cos x = - 1
x 2 Пn, n z48. cos x = 1/2
x3
2 Пn, n z
49. sin x = 1/2
x 1n
6
Пn, n z























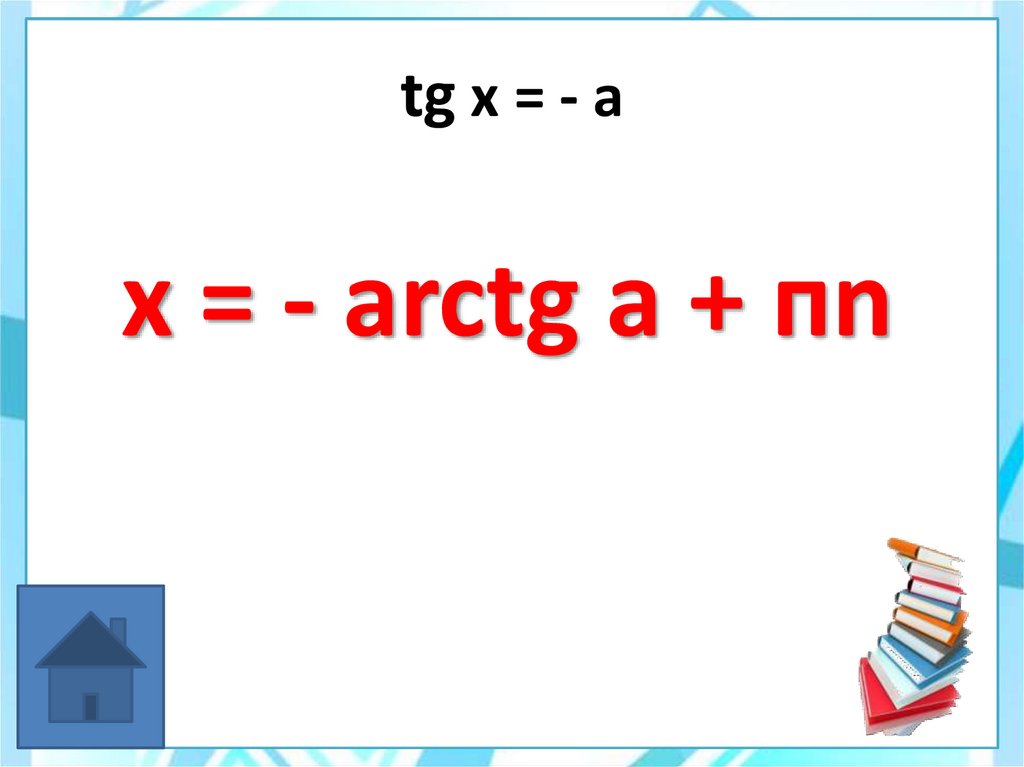


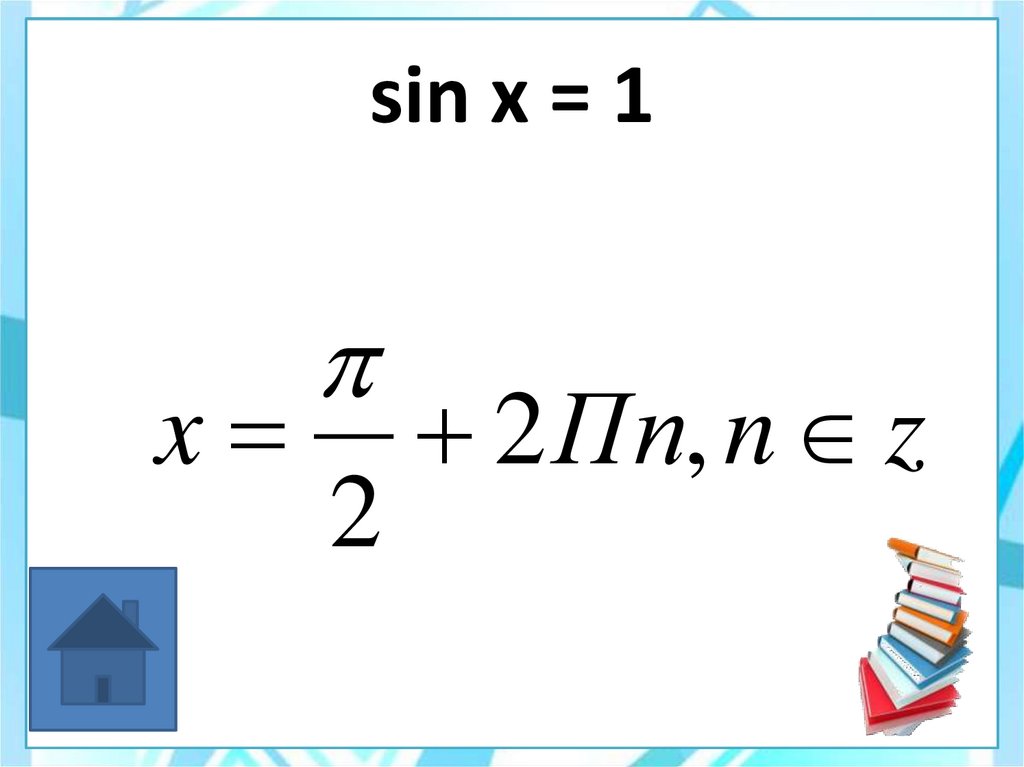
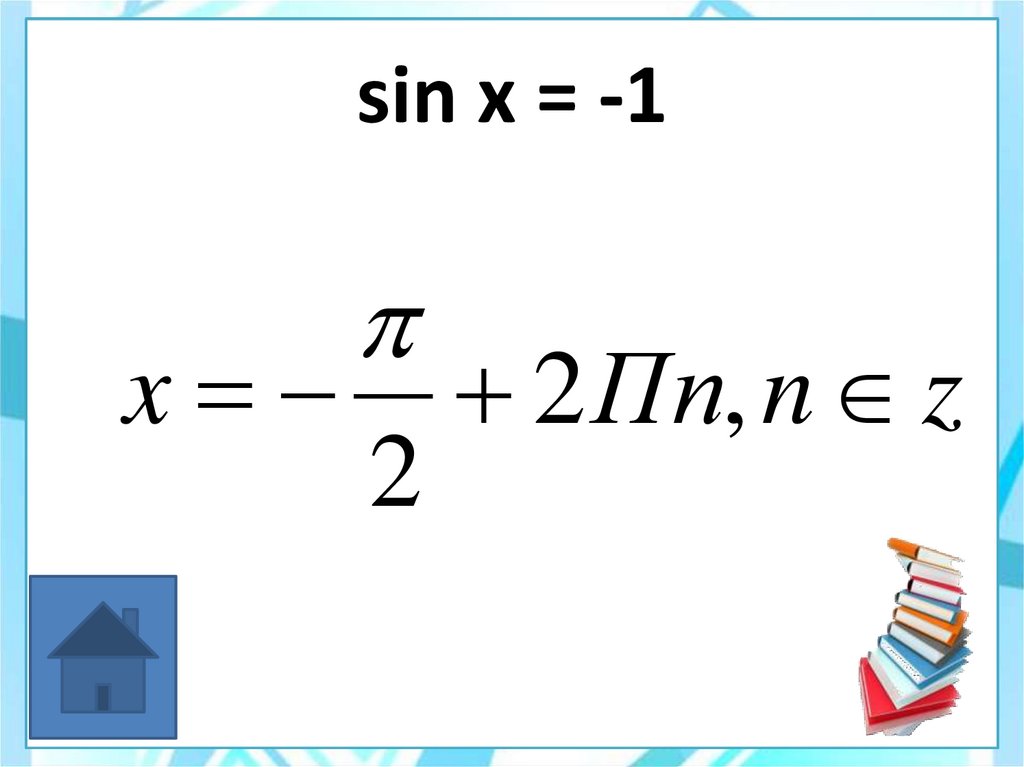



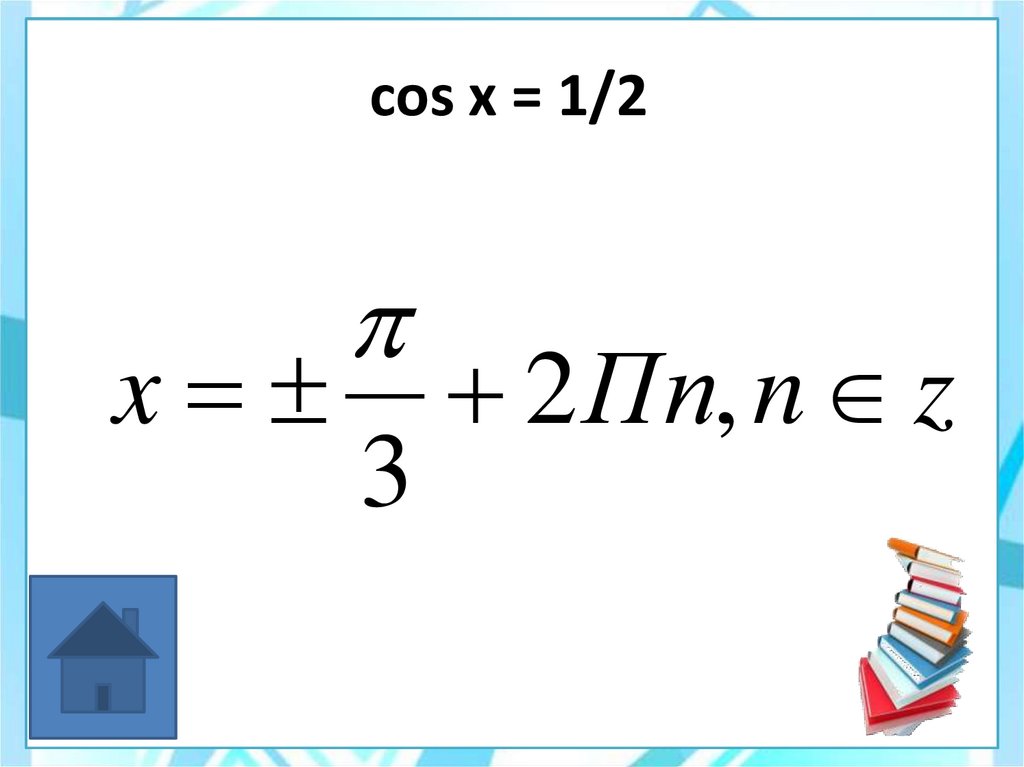
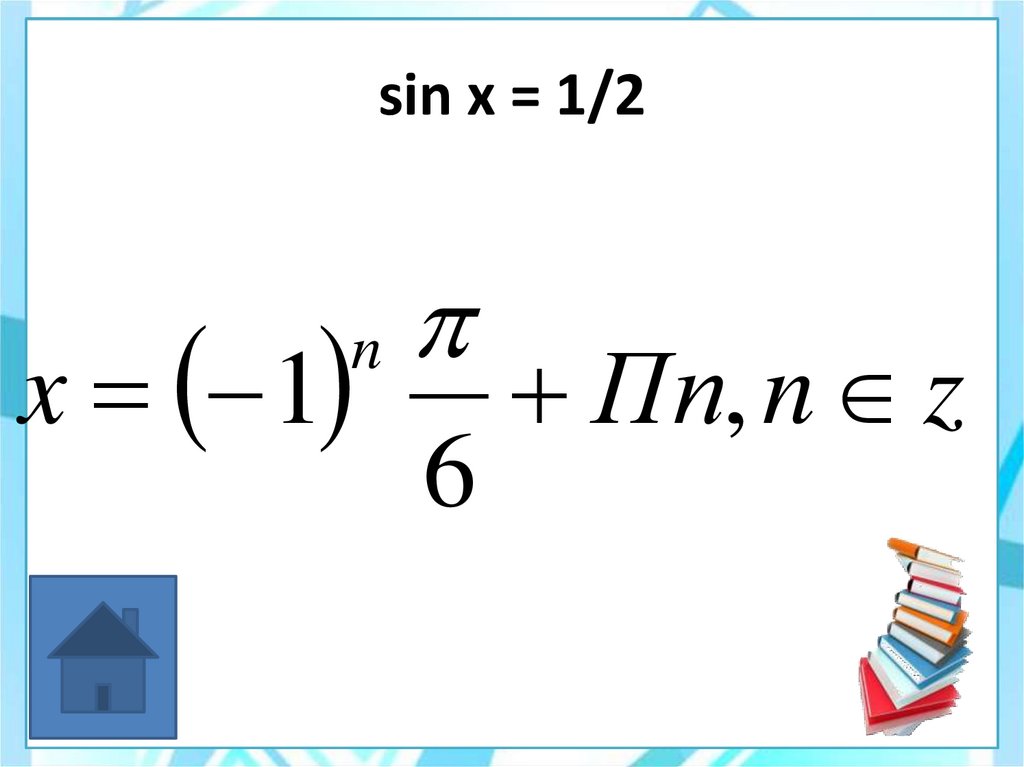

 mathematics
mathematics








