Similar presentations:
Решение простейших тригонометрических уравнений
1. Решение простейших тригонометрических уравнений
2.
1) уметь отмечать точки на числовойокружности;
2) уметь определять значения синуса, косинуса,
тангенса и котангенса для точек числовой
окружности;
3) знать свойства основных
тригонометрических функций;
4) знать понятие арксинуса, арккосинуса,
арктангенса, арккотангенса и уметь отмечать их
на числовой окружности.
3.
Простейшие тригонометрическиеуравнения – это уравнения вида
Cos t = a, Sin t = a, tg t = a, ctg t = a.
4.
yРешим при помощи
числовой окружности
уравнение cos t=a.
1) |а|>1
1
1
1
x
Нет точек пересечения с
окружностью.
Уравнение не имеет
решений.
1
5.
yРешим при помощи
числовой окружности
уравнение cos t=a.
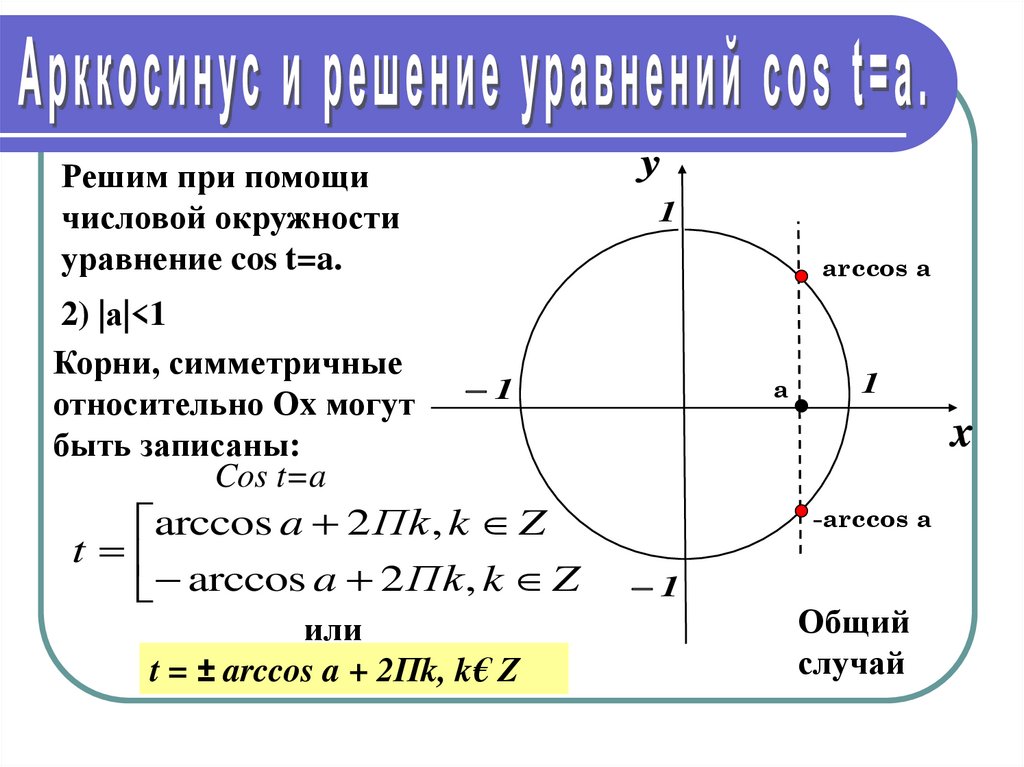
2) |а|<1
Корни, симметричные
относительно Оx могут
быть записаны:
Cos t=a
1
arccos а
1
arccos a 2 Пk , k Z
t
arccos a 2 Пk , k Z
или
t = ± arccos a + 2Пk, k€ Z
а
1
x
-arccos а
1
Общий
случай
6.
yРешим при помощи
числовой окружности
уравнение cos t=a.
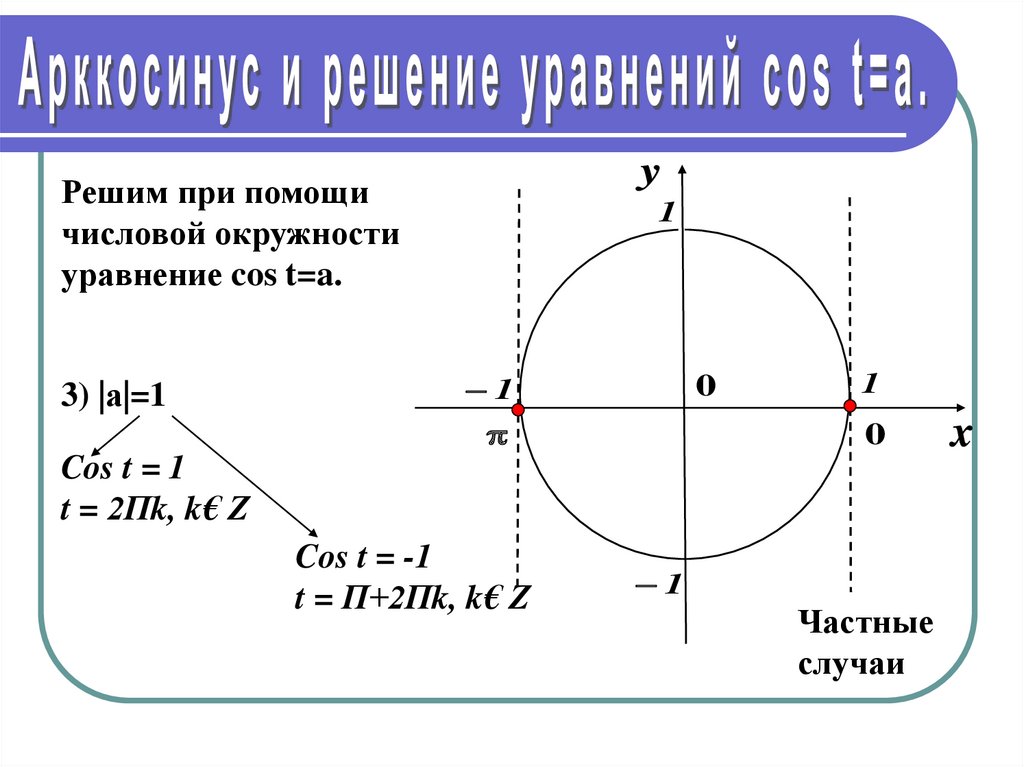
3) |а|=1
1
1
0
1
0
Cos t = 1
t = 2Пk, k€ Z
Cos t = -1
t = П+2Пk, k€ Z
1
Частные
случаи
x
7.
y1 2
Решим при помощи
числовой окружности
уравнение cos t=a.
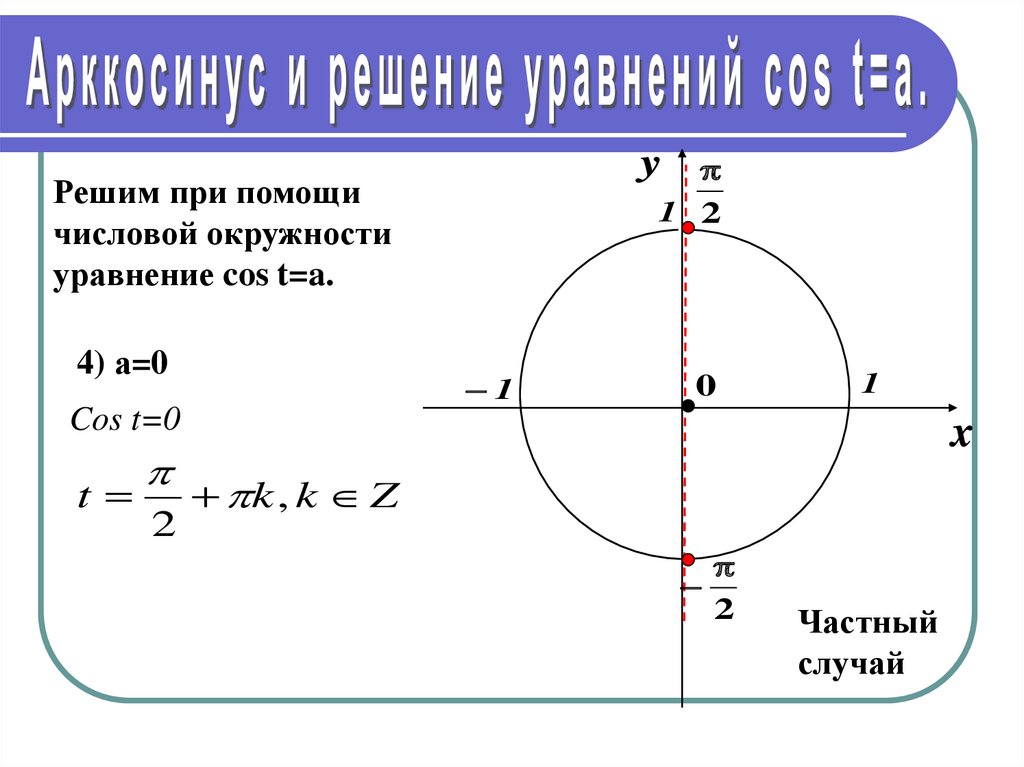
4) а=0
1
0
1
Cos t=0
t
2
x
k , k Z
2
Частный
случай
8.
2 cos 4x 1 0t
1
cos 4 x
,
2
Уравнение переносом
слагаемого и делением обеих
частей легко сводится к
простейшему.
1
4 x arccos
2 k , k
2
4 x 2 k , k
4
Разделим обе части на 4.
x
16
k
2
,k
Ответ:
16
k
2
,k
9.
yРешим при помощи
числовой окружности
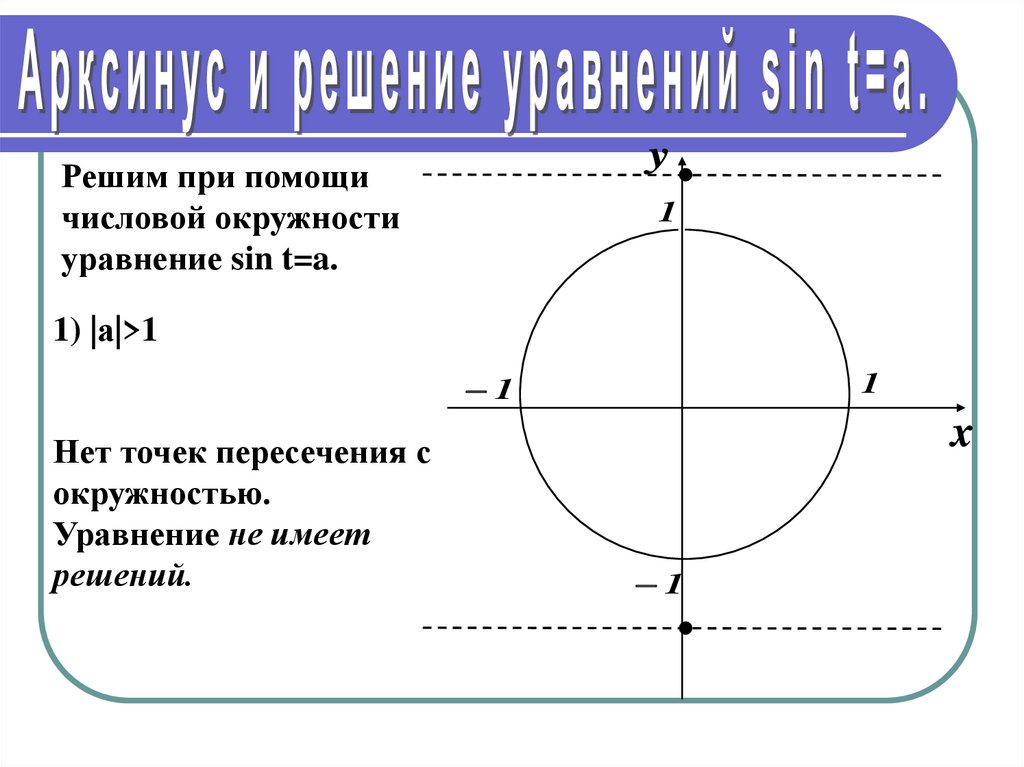
уравнение sin t=a.
1
1) |а|>1
1
Нет точек пересечения с
окружностью.
Уравнение не имеет
решений.
1
x
1
10.
Решим при помощичисловой окружности
уравнение sin t=a.
y
1
П-arcsin а
2) |а|<1
Корни, симметричные
относительно Оу могут
быть записаны: Sin t=a
а
1
arcsin a 2 Пk , k Z
t
П arcsin a 2 Пk , k Z
или
t=(-1)karcsin a+Пk, k€ Z
arcsin а
1
x
1
Общий
случай
11.
yРешим при помощи
числовой окружности
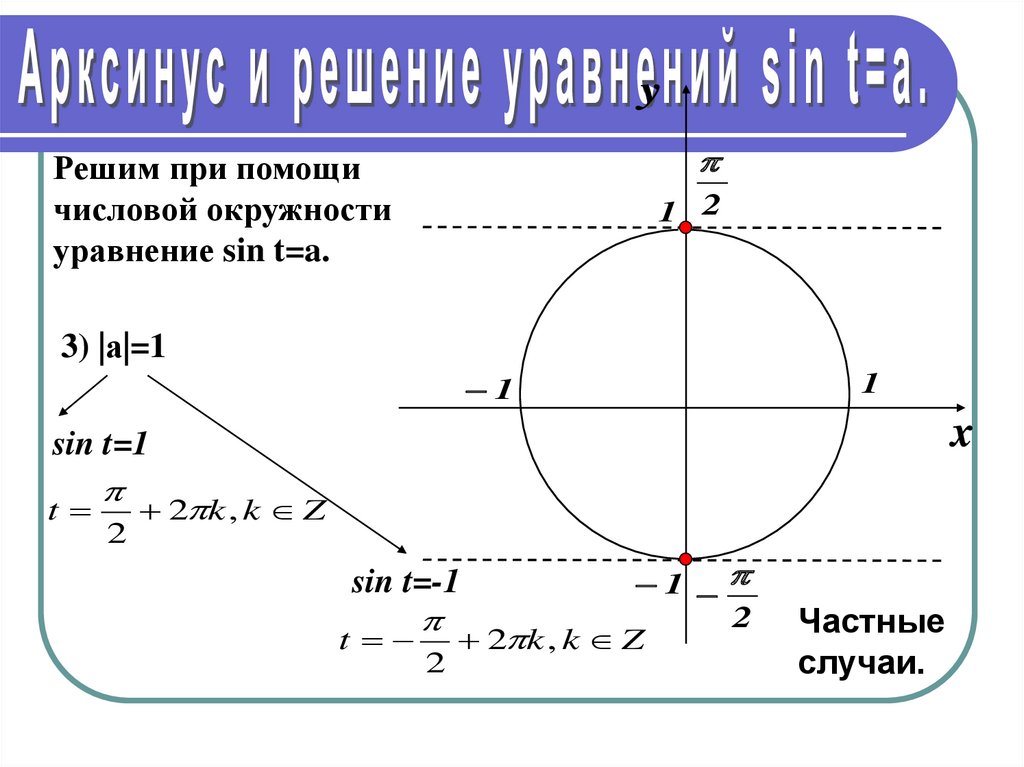
уравнение sin t=a.
1 2
3) |а|=1
1
1
x
sin t=1
t
2
2 k , k Z
1
2
2 k , k Z
sin t=-1
t
2
Частные
случаи.
12.
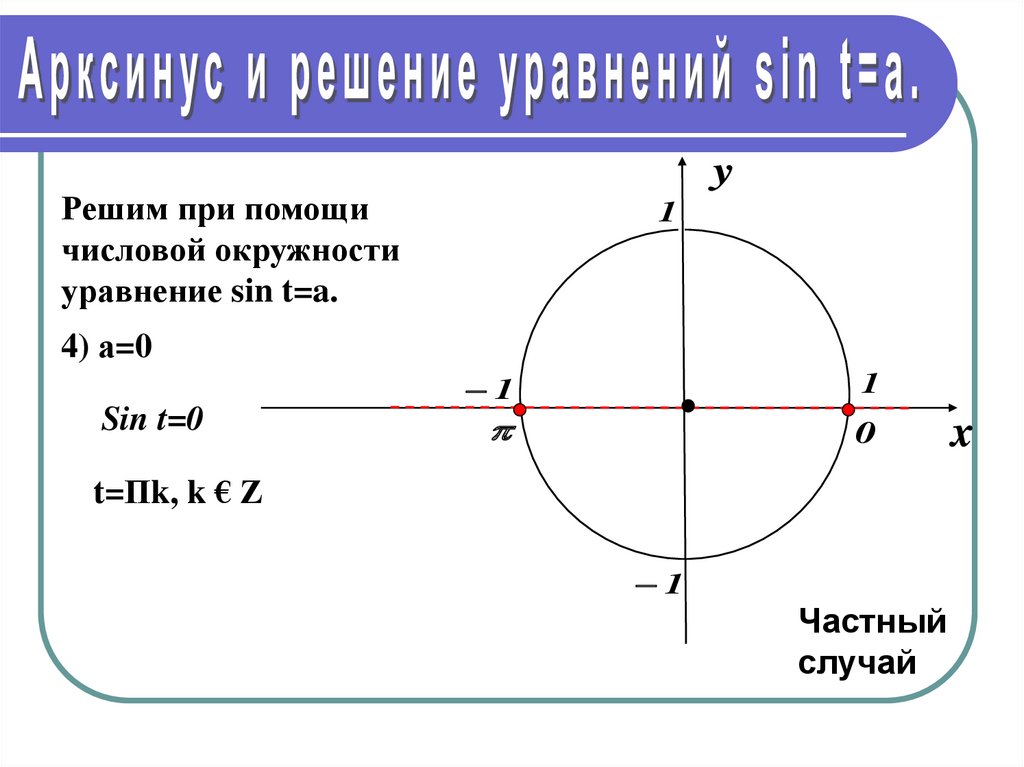
yРешим при помощи
числовой окружности
уравнение sin t=a.
1
4) а=0
Sin t=0
1
1
0
t=Пk, k € Z
1
Частный
случай
x
13.
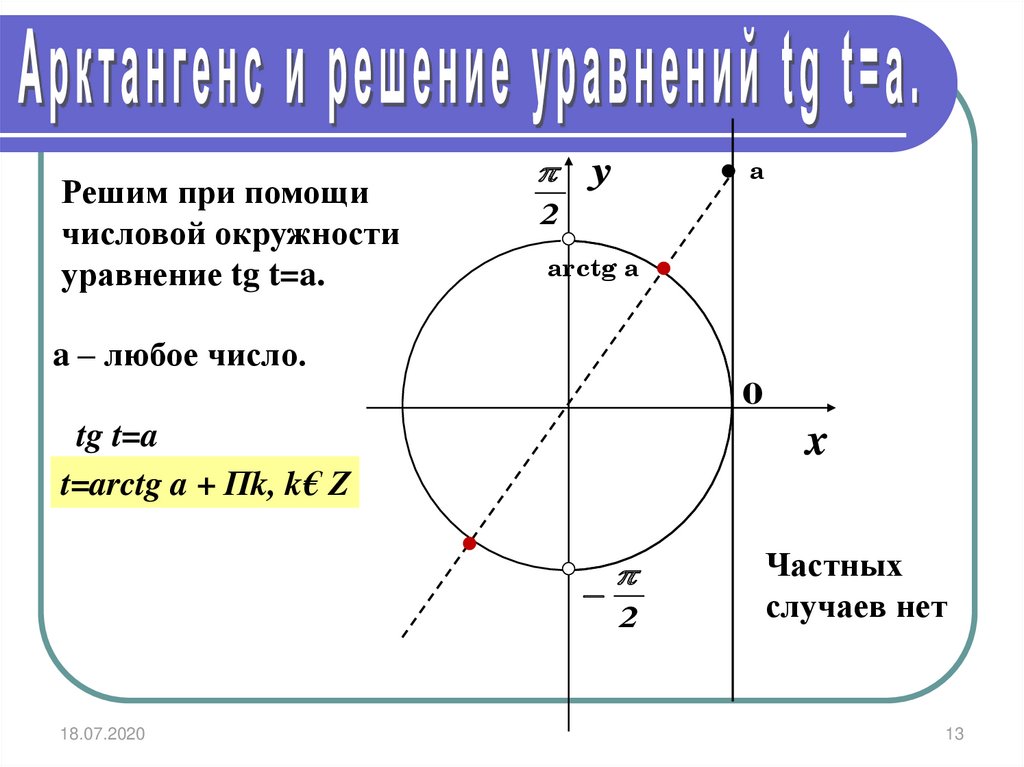
Решим при помощичисловой окружности
уравнение tg t=a.
а
y
2
arctg a
a – любое число.
0
tg t=a
t=arctg a + Пk, k€ Z
x
18.07.2020
2
Частных
случаев нет
13
14.
Решим при помощичисловой окружности
уравнение сtg t=a.
t=arcctg a + Пk, k€ Z
а
arcctg a
a – любое число.
ctg t=a
y
0
x
Частных
случаев нет
18.07.2020
14
15. Простейшие тригонометрические уравнения
Ограничение
Общий вид
|a|> 1,
|a| 1:
корней нет
cos t = a,
t = arccos a+2πk,
kєZ
|a|> 1,
|a| 1:
Частные случаи
a = 1,
cos t = 1,
t = 2πk,
kєZ
корней нет
a = 1,
sin t = a, 0<a< 1,
sin t = 1,
t =(-1)ⁿarcsin a+πn,n є Z t =
+2πk,
2
-1<a< 0
kєZ
t 1 arcsin a k ,
k 1
a = 0,
cos t = 0,
t = + πk,
2 kєZ
a = - 1,
cos t = - 1,
t = π +2πk,
kєZ
a = 0,
sin t = 0,
t = πk,
kєZ
a = - 1,
sin t = -1,
t = - +2πk,
2
kєZ
kєZ
нет
tg t =a,
t = arctg a +πk, k є Z
----
----
----
нет
ctg t = a,
t = arcctg a +πk, k є Z
----
----
----








 mathematics
mathematics








