Similar presentations:
Простейшие тригонометрические уравнения
1.
Простейшиетригонометрические
уравнения
2.
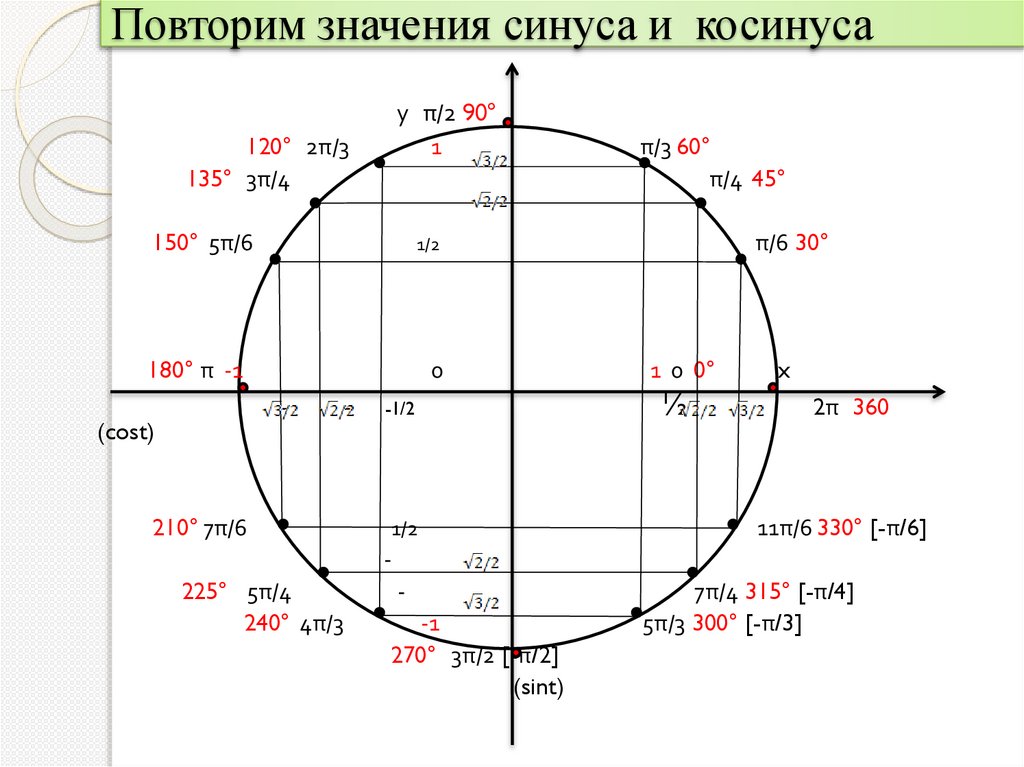
Повторим значения синуса и косинусау π/2 90°
1
120° 2π/3
135° 3π/4
150° 5π/6
1/2
180° π -1
0
-
(cost)
-
210° 7π/6
-1/2
1/2
π/3 60°
π/4 45°
π/6 30°
1 0 0°
½
x
2π 360
11π/6 330° [-π/6]
225° 5π/4
240° 4π/3
-1
270° 3π/2 [-π/2]
(sint)
7π/4 315° [-π/4]
5π/3 300° [-π/3]
3.
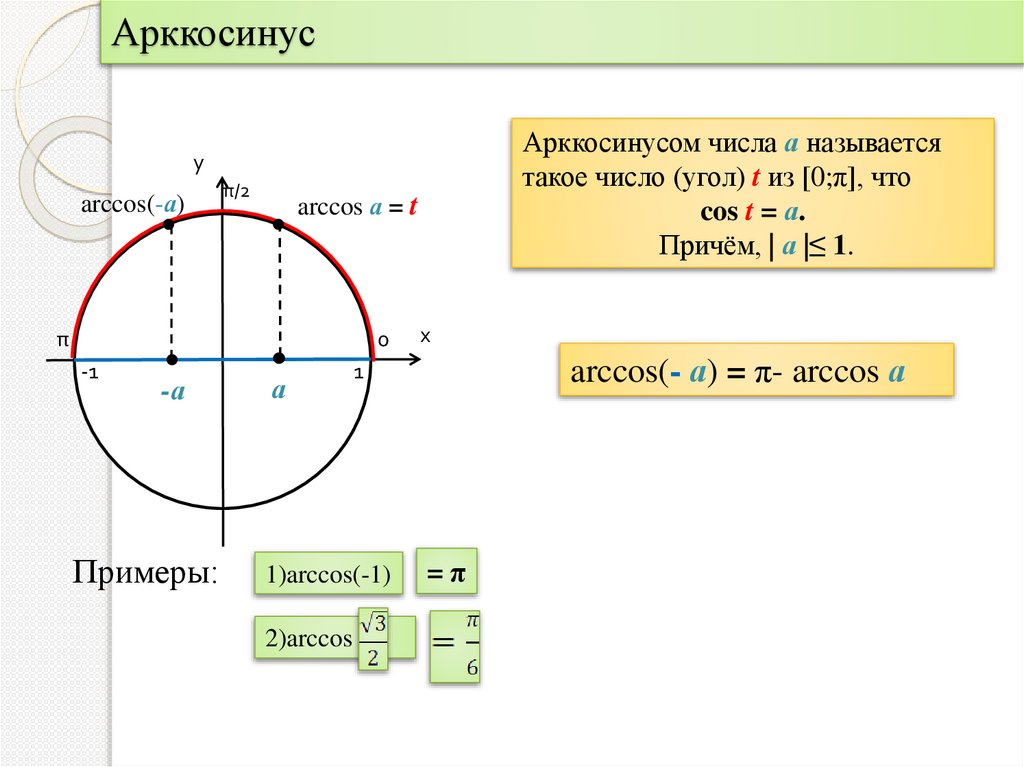
АрккосинусАрккосинусом числа а называется
такое число (угол) t из [0;π], что
cos t = а.
Причём, | а |≤ 1.
у
arccos(-а)
π/2
arccos а = t
π
0
-1
-а
Примеры:
а
arccos(- а) = π- arccos а
1
1)arccos(-1)
2)arccos
х
=π
4.
Уравнение cost = at1
-1
a
1. Проверить условие | a | ≤ 1
y
0
1
x
2. Отметить точку а на оси
абсцисс.
3. Построить перпендикуляр в
этой точке.
4. Отметить точки пересечения
перпендикуляра с окружностью.
5. Полученные точки – решение
уравнения cost = a.
6. Записать общее решение
уравнения.
-t1
t t1 2 n,
n Z
5.
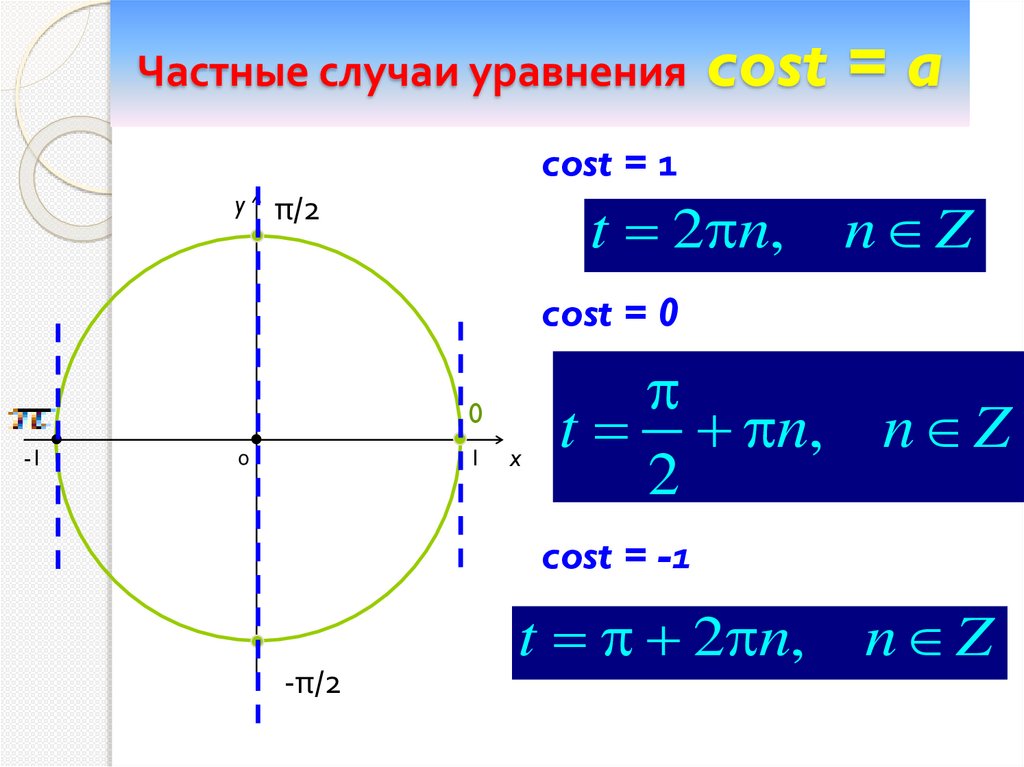
Частные случаи уравнения cost = acost = 1
y
t 2 n,
π/2
n Z
cost = 0
0
-1
1
0
t n, n Z
x
2
cost = -1
t 2 n,
-π/2
n Z
6.
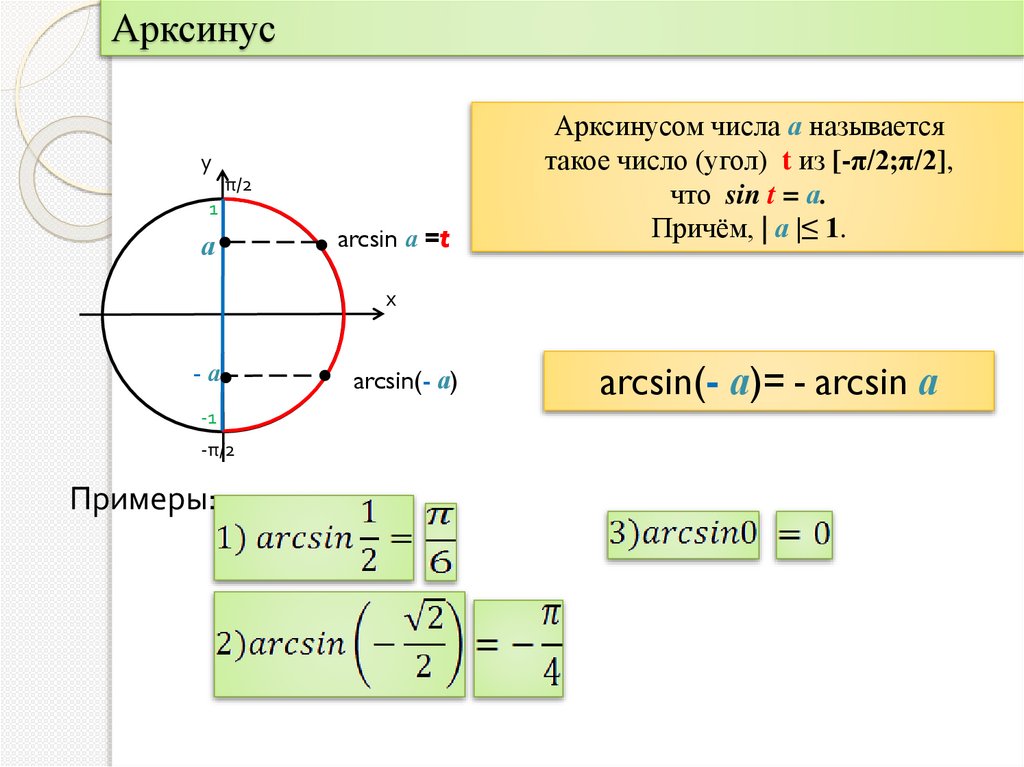
Арксинусу
π/2
1
а
arcsin а =t
Арксинусом числа а называется
такое число (угол) t из [-π/2;π/2],
что sin t = а.
Причём, | а |≤ 1.
х
-а
-1
-π/2
Примеры:
arcsin(- а)
arcsin(- а)= - arcsin а
7.
Уравнение sint = a1. Проверить условие | a | ≤ 1
y
π-t1
2. Отметить точку а на оси
ординат.
1
3. Построить перпендикуляр в
этой точке.
4. Отметить точки пересечения
перпендикуляра с окружностью.
t1
a
0
x
5. Полученные точки – решение
уравнения sint = a.
6. Записать общее решение
уравнения.
-1
t1 2 n, n Z
t
t1 2 n, n Z
8.
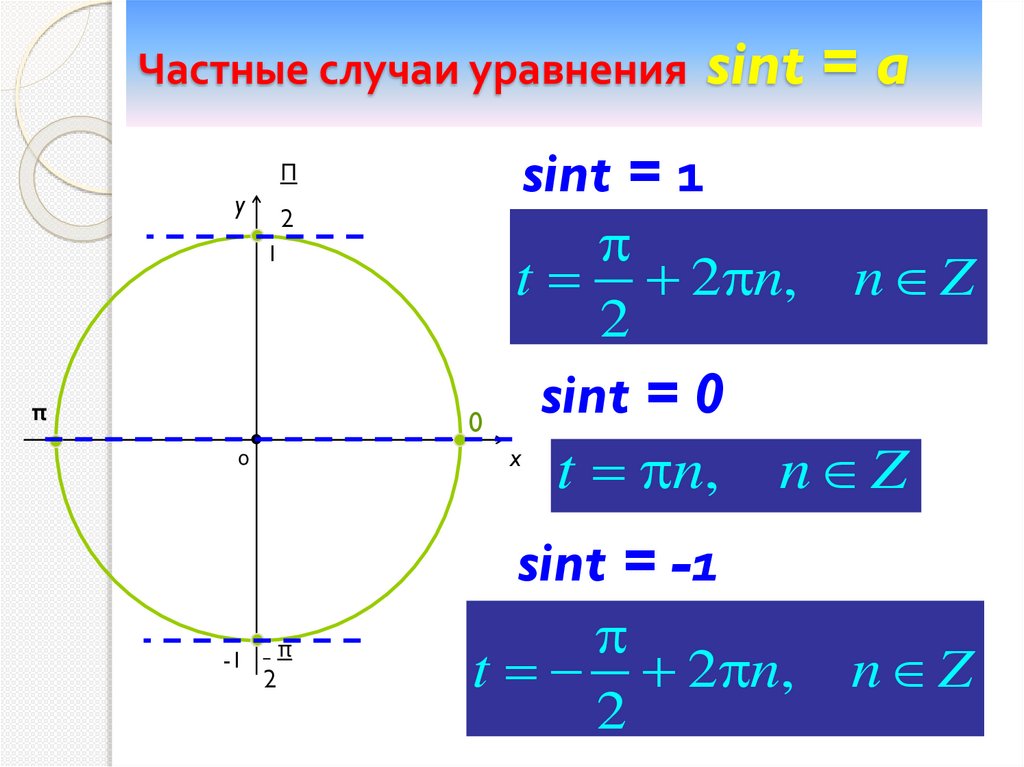
Частные случаи уравнения sint = aΠ
y
2
1
π
0
-1
π
2
sint = 1
t 2 n, n Z
2
sint = 0
0
x
t n, n Z
sint = -1
t 2 n, n Z
2
9.
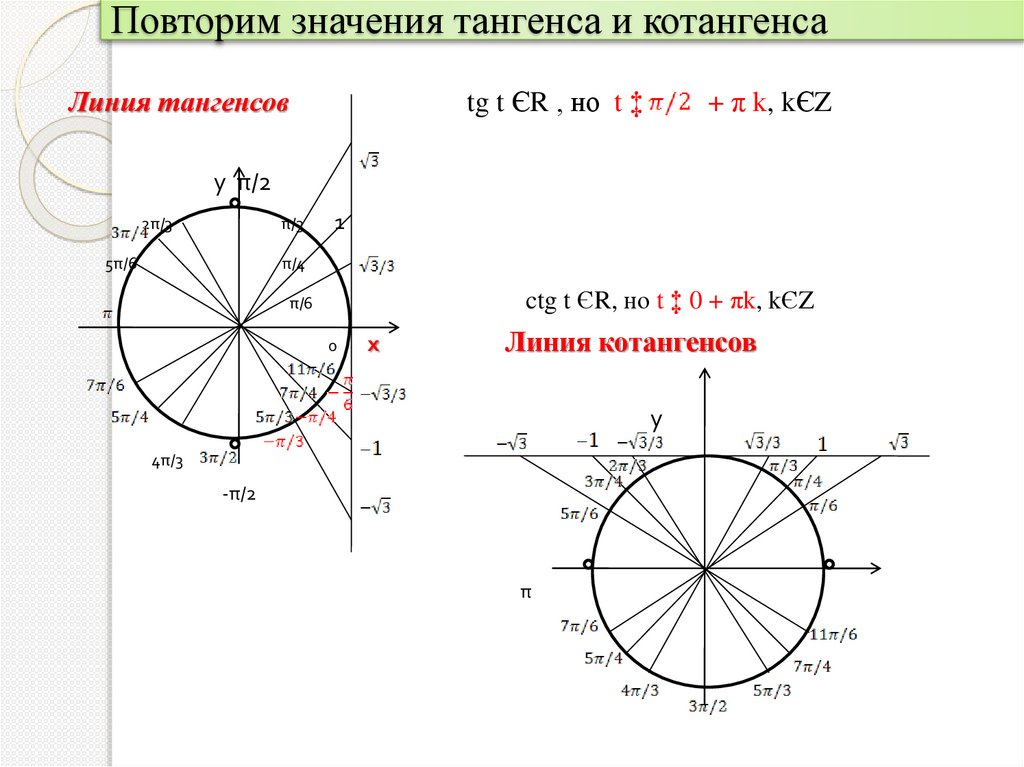
Повторим значения тангенса и котангенсаЛиния тангенсов
tg t ЄR , но t ‡
+ π k, kЄZ
у π/2
2π/3
π/3
5π/6
1
π/4
ctg t ЄR, но t ‡ 0 + πk, kЄZ
π/6
0
х
Линия котангенсов
у
4π/3
-π/2
π
0
х
10.
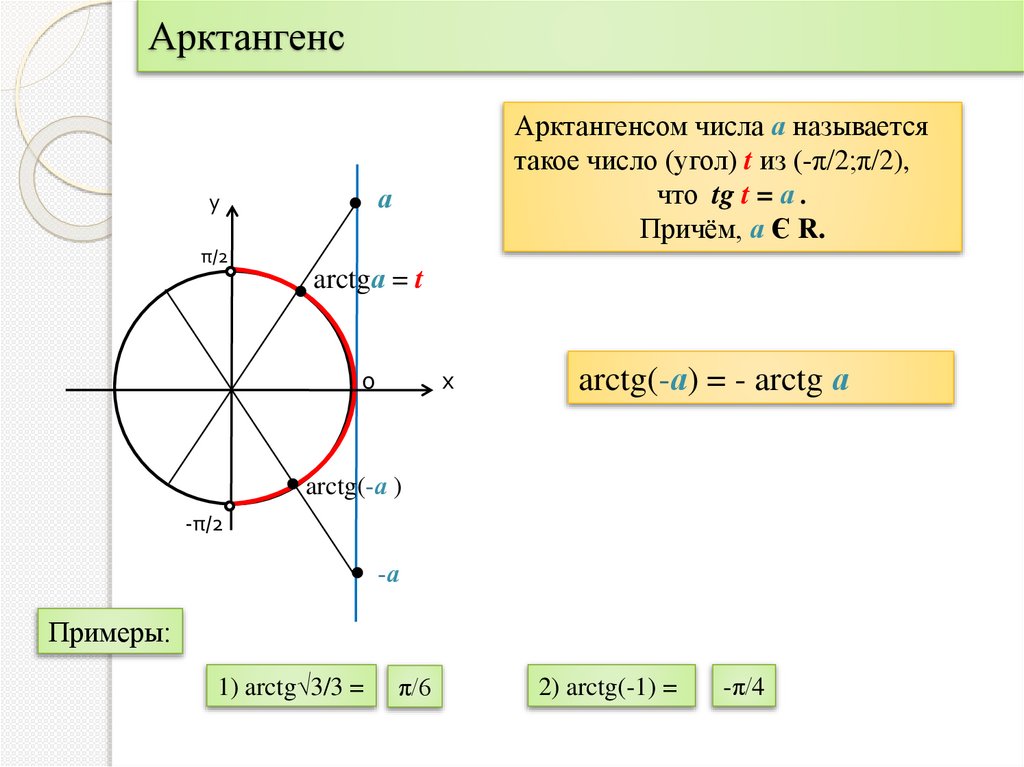
АрктангенсАрктангенсом числа а называется
такое число (угол) t из (-π/2;π/2),
что tg t = а .
Причём, а Є R.
а
у
π/2
arctgа = t
0
х
arctg(-а) = - arctg а
arctg(-а )
-π/2
-а
Примеры:
1) arctg√3/3 =
π/6
2) arctg(-1) =
-π/4
11.
Арккотангенсу
-а
а
arcctg(- а)
arcctg а = t
π
0 х
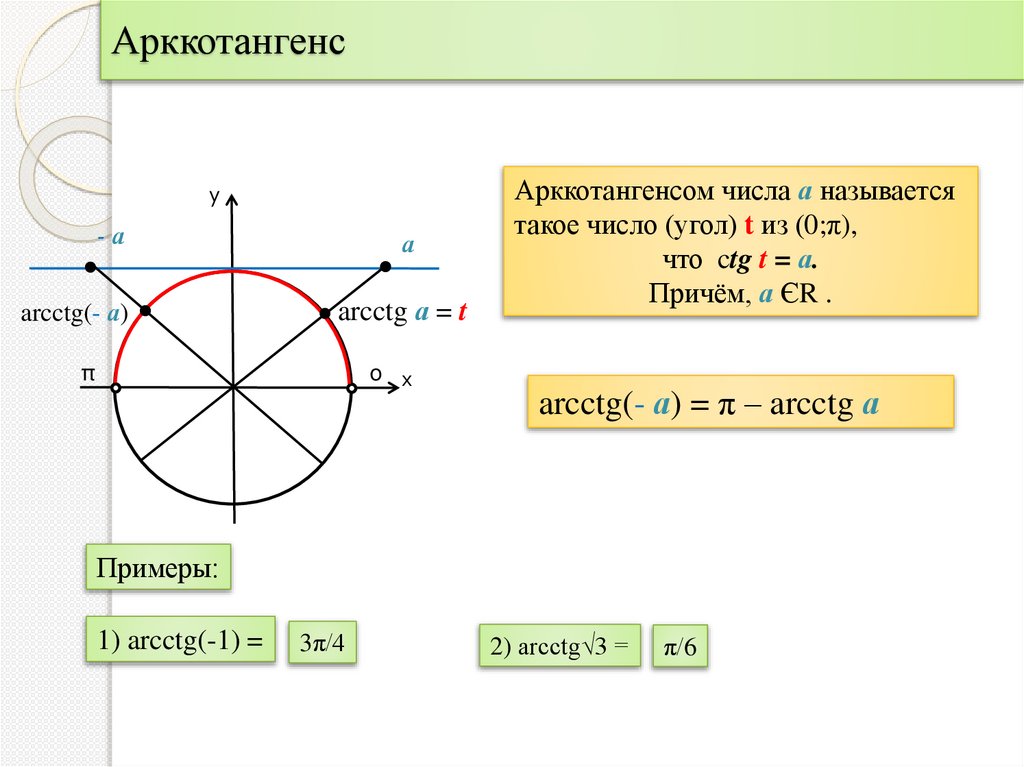
Арккотангенсом числа а называется
такое число (угол) t из (0;π),
что ctg t = а.
Причём, а ЄR .
arcctg(- а) = π – arcctg а
Примеры:
1) arcctg(-1) =
3π/4
2) arcctg√3 =
π/6
12.
Формулы корней простых тригонометрических уравнений1.cost = а , где |а| ≤ 1
или
2.sint = а, где | а |≤ 1
или
Частные случаи
Частные случаи
1)cost=0
t = π/2+πk‚ kЄZ
1)sint=0
t = 0+πk‚ kЄZ
2)cost=1
t = 0+2πk‚ kЄZ
2)sint=1
t = π/2+2πk‚ kЄZ
3)cost = -1
t = π+2πk‚ kЄZ
3)sint = - 1
t = - π/2+2πk‚ kЄZ
3. tgt = а, аЄR
t = arctg а + πk‚ kЄZ
4. ctgt = а, аЄR
t = arcctg а + πk‚ kЄZ
13.
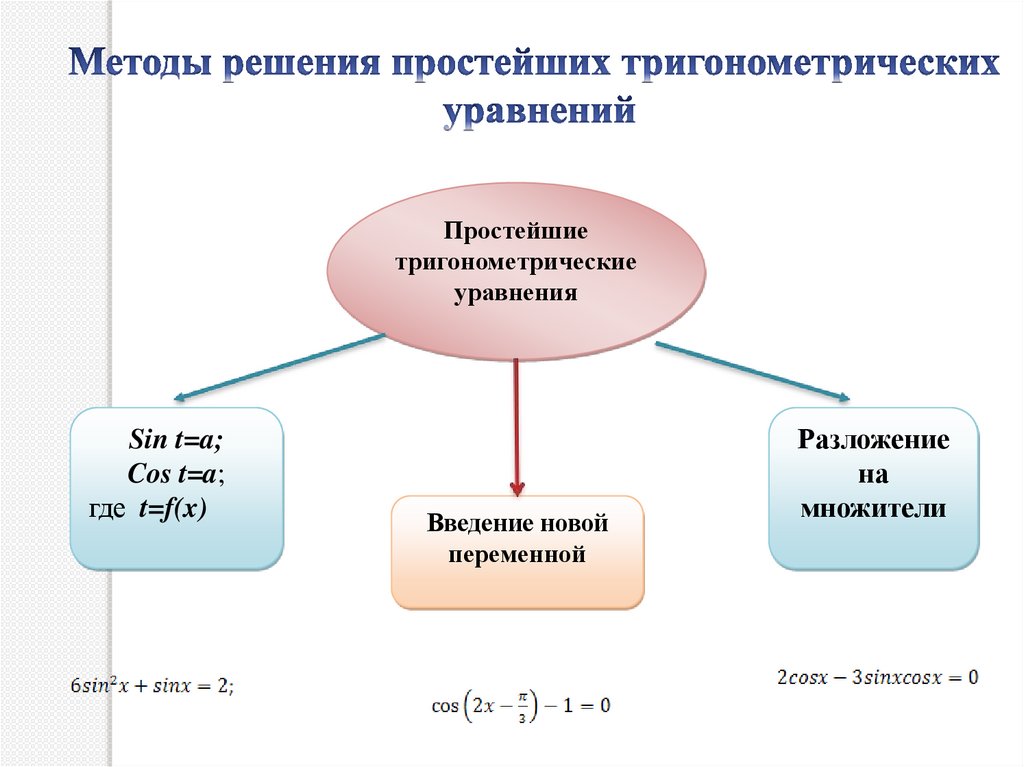
Простейшиетригонометрические
уравнения
Sin t=a;
Cos t=a;
где t=f(x)
Введение новой
переменной
Разложение
на
множители
14.
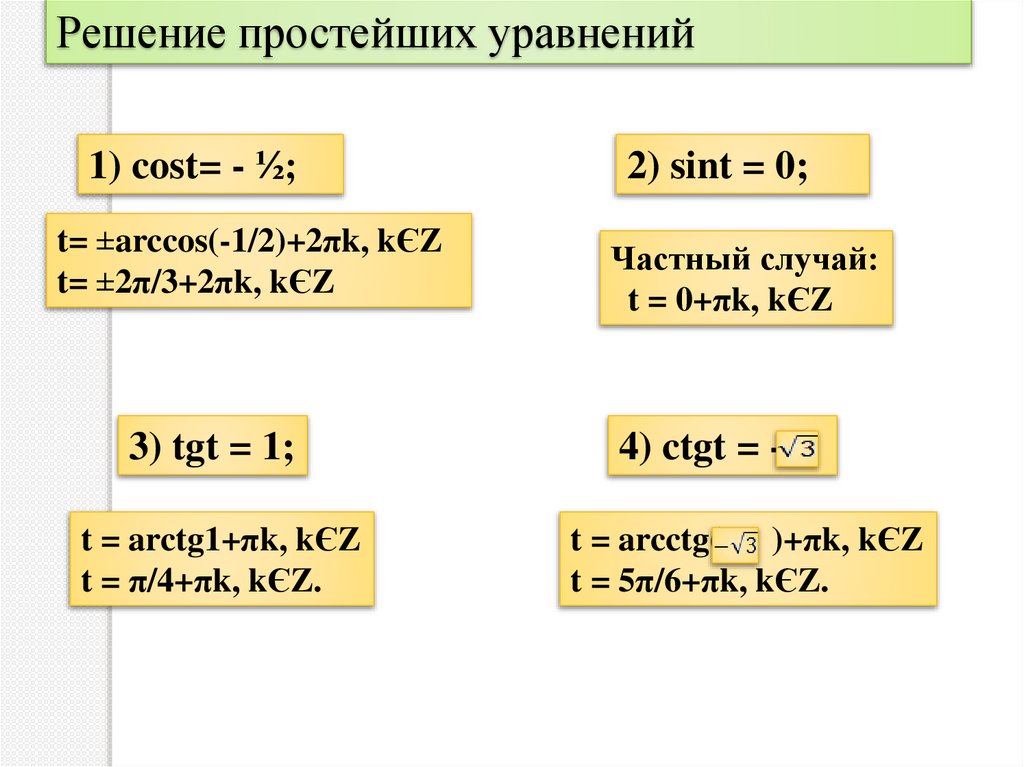
Решение простейших уравнений1) cost= - ½;
t= ±arccos(-1/2)+2πk, kЄZ
t= ±2π/3+2πk, kЄZ
3) tgt = 1;
t = arctg1+πk, kЄZ
t = π/4+πk, kЄZ.
2) sint = 0;
Частный случай:
t = 0+πk, kЄZ
4) ctgt = t = arcctg( )+πk, kЄZ
t = 5π/6+πk, kЄZ.
15.
Решение простейших уравнений1) tg2x = -1
2) cos(x+π/3) = ½
2x = arctg (-1) + πk, kЄZ
2x = -π/4 + πk, kЄZ
x = -π/8 + πk/2, kЄZ
x+π/3 = ±arccos1/2 + 2πk, kЄZ
x+π/3 = ±π/3 + 2πk, kЄZ
x = -π/3 ± π/3 + 2πk, kЄZ
Ответ: -π/8 + πk/2, kЄZ.
Ответ: -π/3 ± π/3 + 2πk, kЄZ
3) sin(π – x/3) = 0
упростим по формулам
приведения
sin(x/3) = 0
частный случай
x/3 = πk, kЄZ
x = 3πk, kЄZ.
Ответ: 3πk, kЄZ.
16.
Домашнее заданиеВыучить формулы корней простых
тригонометрических уравнений и записать конспект






 mathematics
mathematics








