Similar presentations:
Поверхности. Способ задания поверхности
1. Поверхности
Московский государственныйтехнический университет
им. Н.Э. Баумана
Кафедра
«Инженерная графика»
Горячкина А.Ю.
Корягина О.М.
2.
Поверхность – непрерывная совокупность последовательных положений некоторойдвижущейся в пространстве линии.
Все поверхности можно изобразить на плоскости, задавая проекции линий и точек,
принадлежащих поверхности.
Поверхность считается заданной на чертеже, если можно построить проекцию
любой точки, ей принадлежащей.
Задание поверхности на чертеже
1. Каркасом – семейством линий или точек
2. Определителем – совокупностью геометрических элементов, позволяющих
реализовать закон образования поверхности
3. Очерком – проекцией контурной линии поверхности
Московский государственный
технический университет
им. Н.Э. Баумана
3.
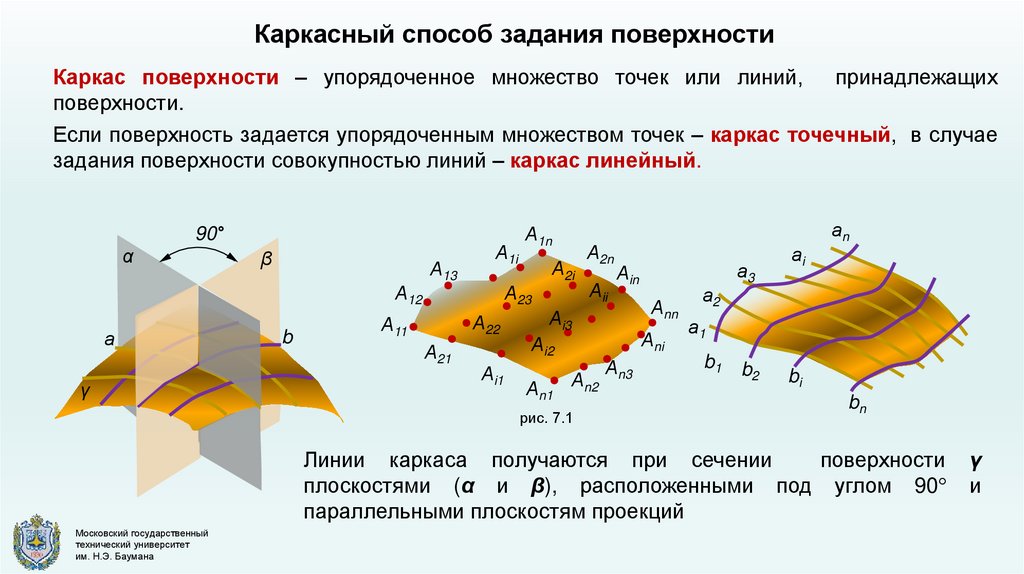
Каркасный способ задания поверхностиКаркас поверхности – упорядоченное множество точек или линий, принадлежащих
поверхности.
Если поверхность задается упорядоченным множеством точек – каркас точечный, в случае
задания поверхности совокупностью линий – каркас линейный.
90°
α
β
А12
а
γ
b
А13
А1i
А23
А22
А11
А21
А1n
Аi1
А2i
А2n
Аii
Аin
Аi3
Аi2
Аn1
Аn2
рис. 7.1
Аnn
Аni
Аn3
а2
а3
аi
аn
а1
b1
b2
bi
bn
Линии каркаса получаются при сечении
поверхности
плоскостями (α и β), расположенными под углом 90°
параллельными плоскостям проекций
Московский государственный
технический университет
им. Н.Э. Баумана
γ
и
4.
Кинематический способ образования поверхностейПоверхность – непрерывная совокупность последовательных положений линии gj ,
перемещающейся в пространстве по определенному закону.
Образующая ( g ) – линия (прямая или кривая), которая при своем движении образует
поверхность.
Направляющие (d ) – линии (прямые или кривые), задающие направление (закон)
движения образующей.
g
d1
d2
d3
Рис. 7.2
Признак принадлежности точки поверхности
Если точка принадлежит поверхности, то проекции точки принадлежат одноименным
проекциям линии, лежащей на поверхности
Московский государственный
технический университет
им. Н.Э. Баумана
5.
Определитель поверхностиОпределитель поверхности – необходимая и достаточная совокупность независимых
условий, однозначно задающих поверхность.
Ф (Г); [A]
(Г) – геометрическая часть ( содержит перечень геометрических фигур, участвующих в
задании поверхности, и отношений между ними);
[A] – алгоритмическая часть ( описывает закон движения и изменения образующей).
На чертеже поверхность задают проекциями геометрических фигур, входящих в состав
геометрической части определителя.
Ф (g, d1 , d2 , d3); [gi ∩ {d1 , d2 , d3} ≠ Ø] (рис. 7.2)
Московский государственный
технический университет
им. Н.Э. Баумана
6.
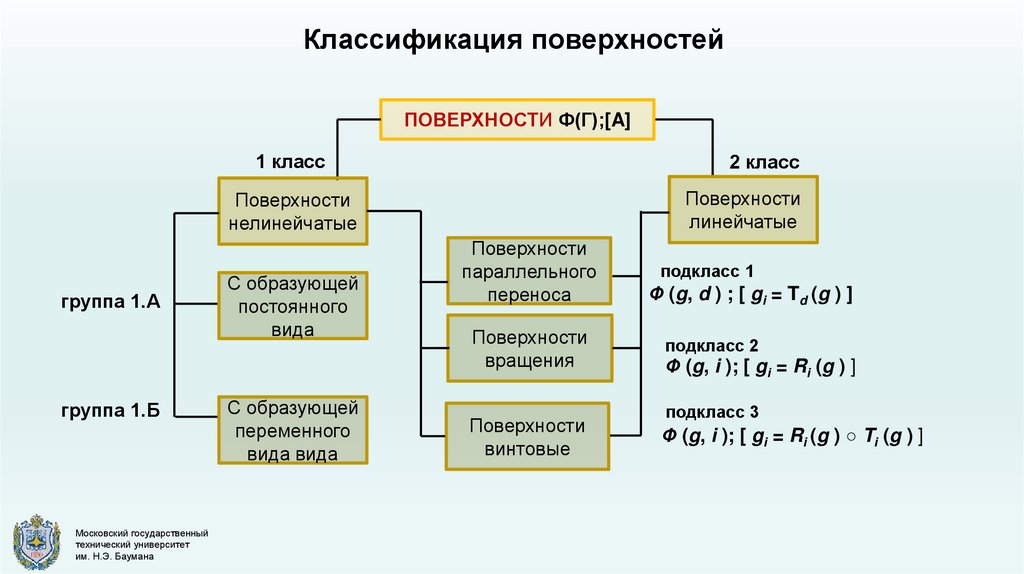
Классификация поверхностейПОВЕРХНОСТИ Ф(Г);[A]
1 класс
2 класс
Поверхности
линейчатые
Поверхности
нелинейчатые
группа 1.А
группа 1.Б
Московский государственный
технический университет
им. Н.Э. Баумана
С образующей
постоянного
вида
С образующей
переменного
вида вида
Поверхности
параллельного
переноса
Поверхности
вращения
Поверхности
винтовые
подкласс 1
Ф (g, d ) ; [ gi = Td (g ) ]
подкласс 2
Ф (g, i ); [ gi = Ri (g ) ]
подкласс 3
Ф (g, i ); [ gi = Ri (g ) ○ Ti (g ) ]
7.
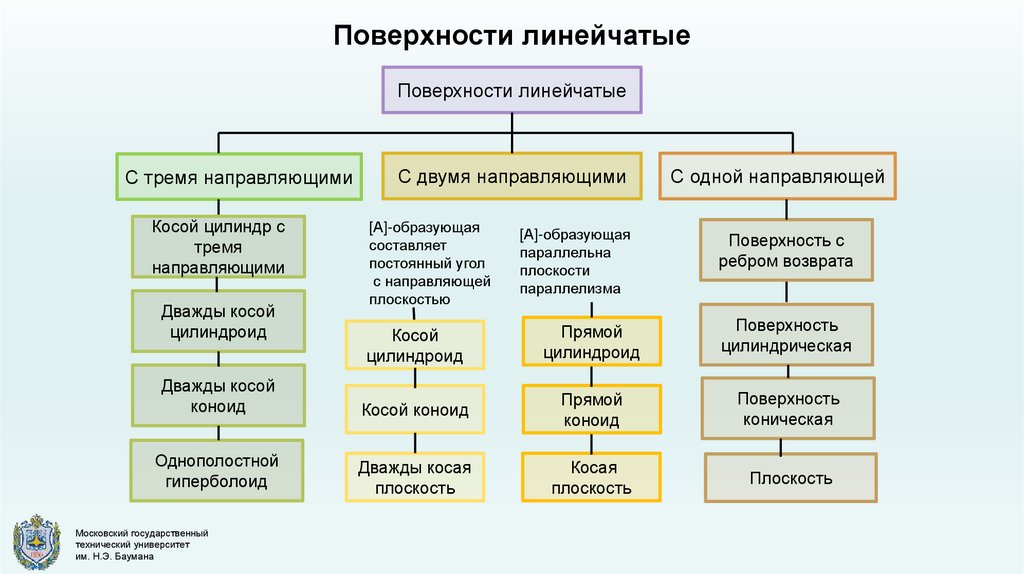
Поверхности линейчатыеПоверхности линейчатые
С тремя направляющими
Косой цилиндр с
тремя
направляющими
Дважды косой
цилиндроид
С двумя направляющими
[А]-образующая
составляет
постоянный угол
с направляющей
плоскостью
[А]-образующая
параллельна
плоскости
параллелизма
С одной направляющей
Поверхность с
ребром возврата
Косой
цилиндроид
Прямой
цилиндроид
Поверхность
цилиндрическая
Дважды косой
коноид
Косой коноид
Прямой
коноид
Поверхность
коническая
Однополостной
гиперболоид
Дважды косая
плоскость
Косая
плоскость
Плоскость
Московский государственный
технический университет
им. Н.Э. Баумана
8.
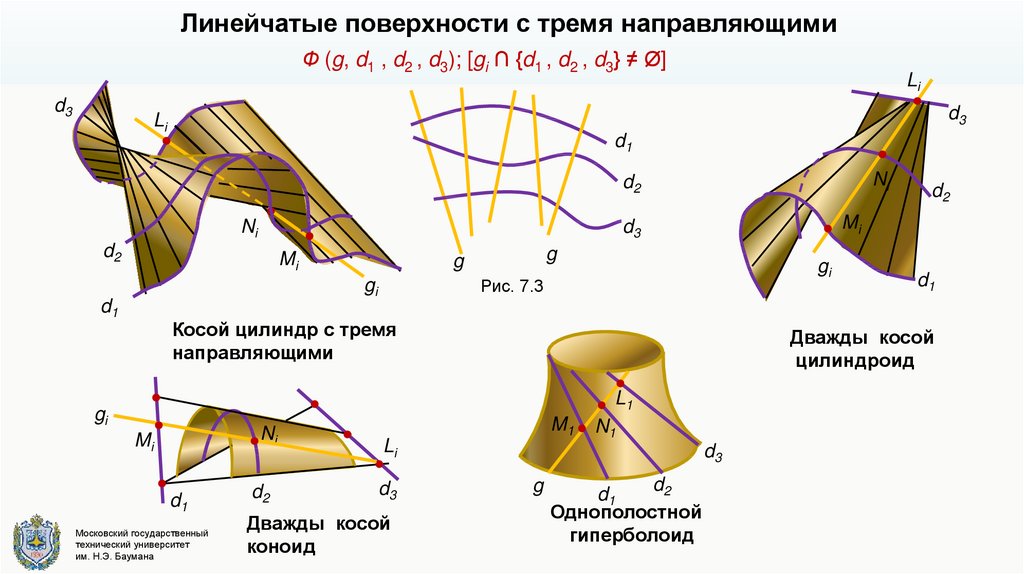
Линейчатые поверхности с тремя направляющимиФ (g, d1 , d2 , d3); [gi ∩ {d1 , d2 , d3} ≠ Ø]
d3
Li
d3
Li
d1
Ni
d2
Ni
Mi
g
g
gi
Рис. 7.3
gi
d1
Mi
d3
d2
Косой цилиндр с тремя
направляющими
Ni
Mi
d1
Московский государственный
технический университет
им. Н.Э. Баумана
d2
M1
Li
d3
Дважды косой
коноид
d1
Дважды косой
цилиндроид
L1
gi
d2
N1
d3
g
d2
d1
Однополостной
гиперболоид
9.
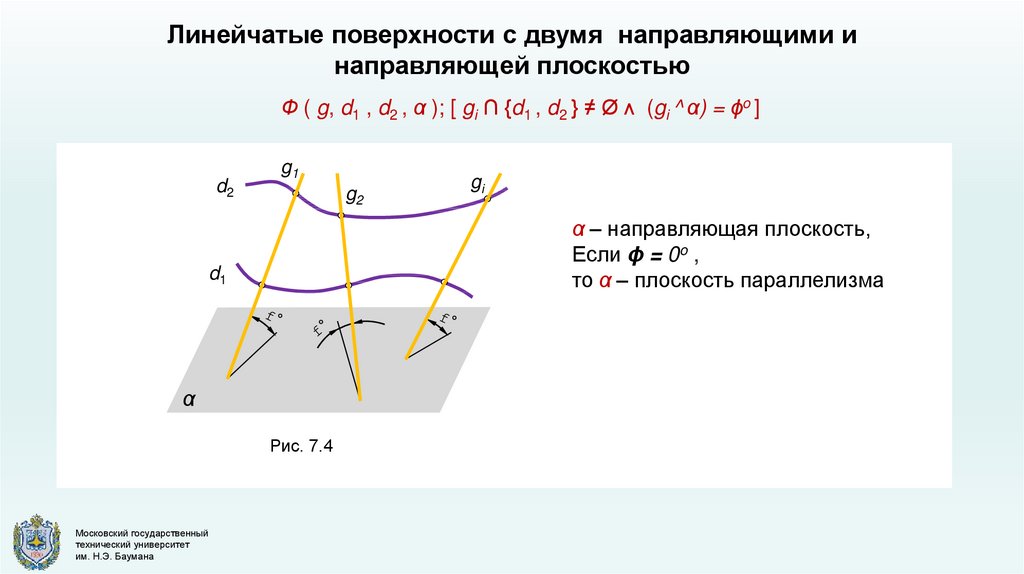
Линейчатые поверхности с двумя направляющими инаправляющей плоскостью
Ф ( g, d1 , d2 , α ); [ gi ∩ {d1 , d2 } ≠ Ø ᴧ (gi ^ α) = ϕo ]
d2
g1
g2
α – направляющая плоскость,
Если ϕ = 0o ,
то α – плоскость параллелизма
d1
α
Рис. 7.4
Московский государственный
технический университет
им. Н.Э. Баумана
gi
10.
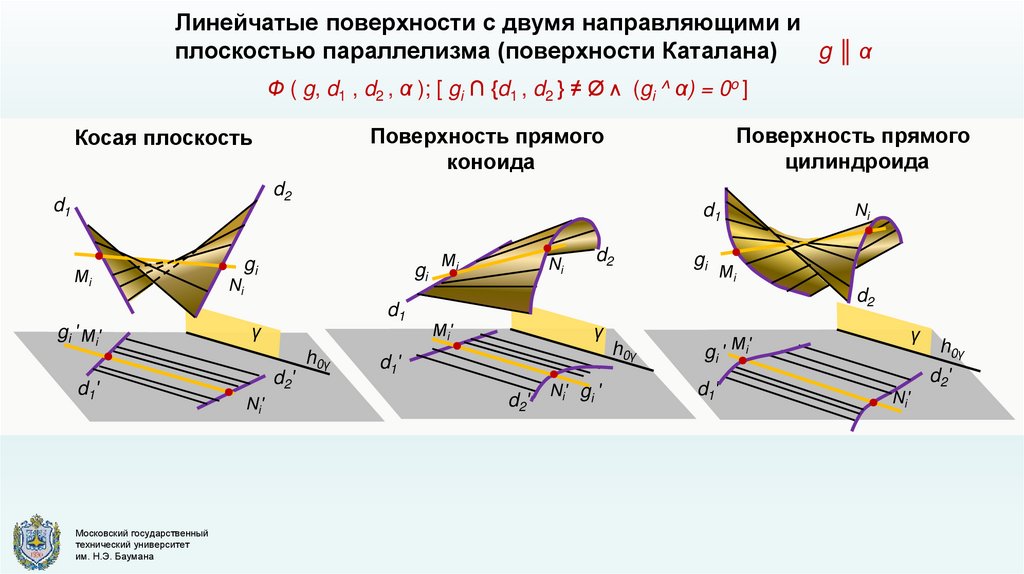
Линейчатые поверхности с двумя направляющими иплоскостью параллелизма (поверхности Каталана)
g║α
Ф ( g, d1 , d2 , α ); [ gi ∩ {d1 , d2 } ≠ Ø ᴧ (gi ^ α) = 0o ]
Поверхность прямого
цилиндроида
Поверхность прямого
коноида
Косая плоскость
d2
d1
Мi
gi ′ Мi′
d1′
Московский государственный
технический университет
им. Н.Э. Баумана
d1
gi
gi
Ni
d1
γ
d2′
Ni′
h0γ
Мi
Ni
d2
gi
Ni
Мi
d2
Мi′
γ
d1′
d2′
Ni′ gi ′
h0γ
gi ′
d1′
γ
М i′
Ni′
h0γ
d2′
11.
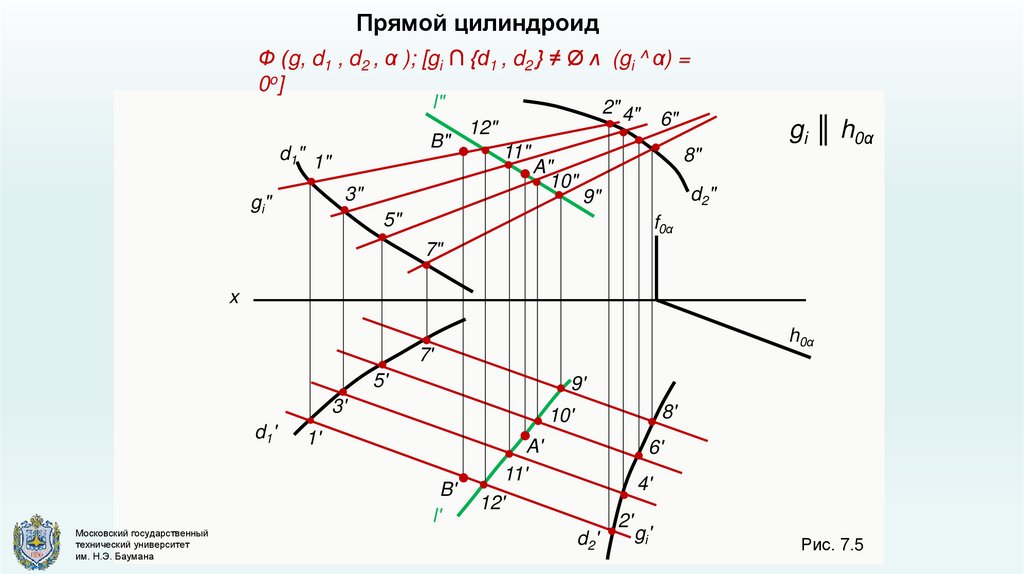
Прямой цилиндроидФ (g, d1 , d2 , α ); [gi ∩ {d1 , d2 } ≠ Ø ᴧ (gi ^ α) =
0o ]
l"
B"
d1" 1"
3"
gi"
2" 4"
12"
11"
A"
10"
6"
8"
gi ║ h0α
d2"
9"
5"
f0α
7"
x
h0α
7'
5'
9'
3'
d1'
1'
B'
l'
Московский государственный
технический университет
им. Н.Э. Баумана
8'
10'
A'
11'
12'
6'
4'
d2'
2'
gi'
Рис. 7.5
12.
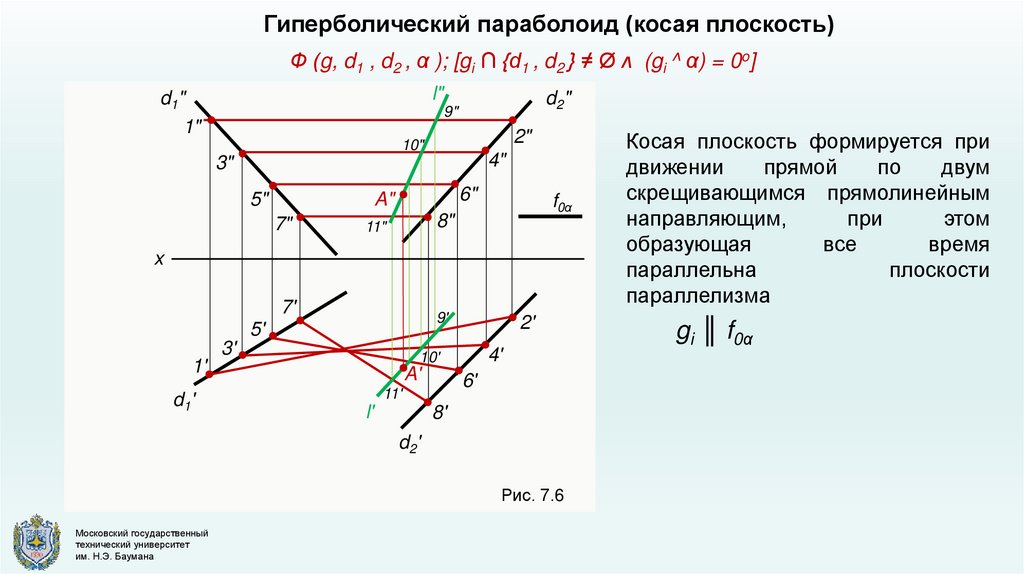
Гиперболический параболоид (косая плоскость)Ф (g, d1 , d2 , α ); [gi ∩ {d1 , d2 } ≠ Ø ᴧ (gi ^ α) = 0o]
l"
d1"
1"
d2"
9"
2"
10"
4"
3"
5"
6"
A"
7"
f0α
8"
11"
x
7'
9'
5'
3'
4'
10'
1'
d1'
2'
A'
6'
11'
l'
8'
d2'
Рис. 7.6
Московский государственный
технический университет
им. Н.Э. Баумана
Косая плоскость формируется при
движении
прямой
по
двум
скрещивающимся прямолинейным
направляющим,
при
этом
образующая
все
время
параллельна
плоскости
параллелизма
gi ║ f0α
13.
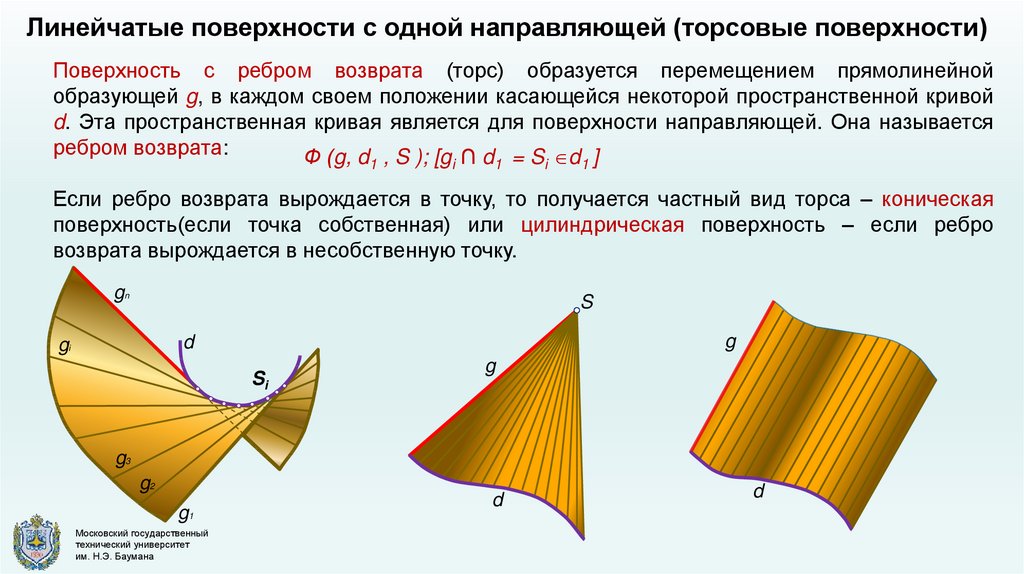
Линейчатые поверхности с одной направляющей (торсовые поверхности)Поверхность с ребром возврата (торс) образуется перемещением прямолинейной
образующей g, в каждом своем положении касающейся некоторой пространственной кривой
d. Эта пространственная кривая является для поверхности направляющей. Она называется
ребром возврата:
Ф (g, d , S ); [g ∩ d = S d ]
1
i
1
i
1
Если ребро возврата вырождается в точку, то получается частный вид торса – коническая
поверхность(если точка собственная) или цилиндрическая поверхность – если ребро
возврата вырождается в несобственную точку.
gn
S
g
d
gi
Si
g
g3
g2
g1
Московский государственный
технический университет
им. Н.Э. Баумана
d
d
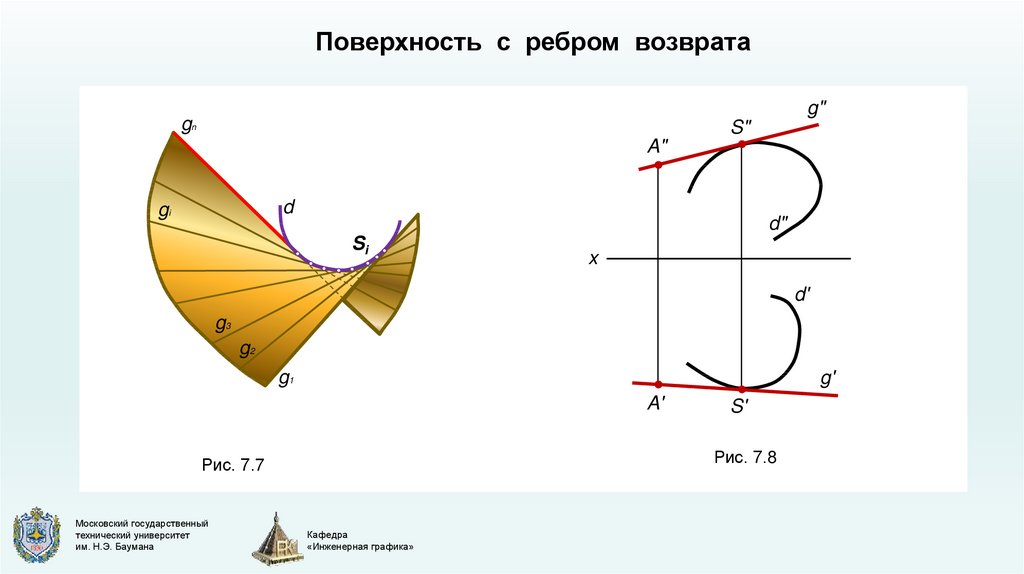
14.
Поверхность с ребром возвратаg"
gn
S"
A"
d
gi
d"
Si
x
d'
g3
g2
g1
g'
A'
Рис. 7.8
Рис. 7.7
Московский государственный
технический университет
им. Н.Э. Баумана
S'
Кафедра
«Инженерная графика»
15.
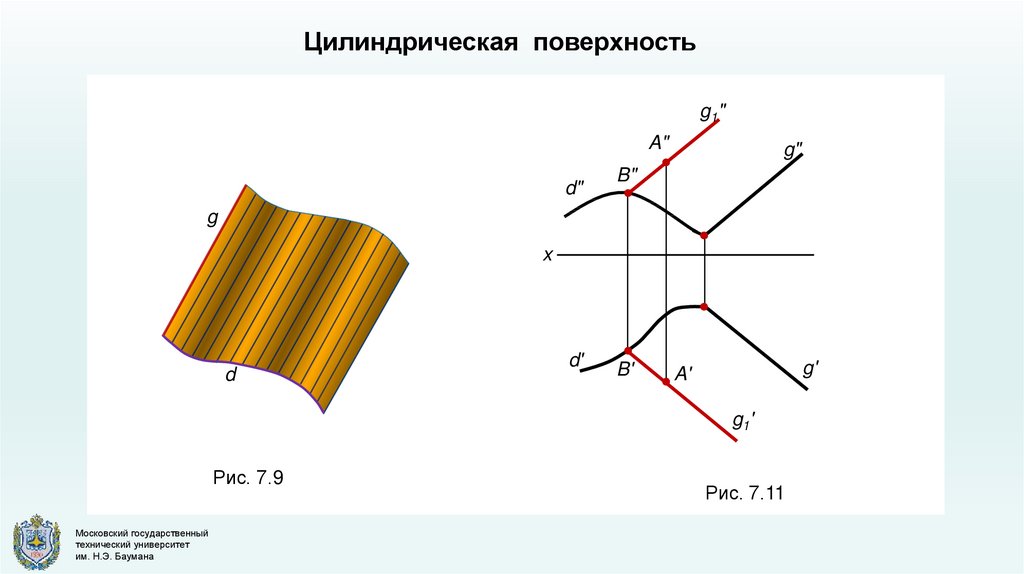
Цилиндрическая поверхностьg1"
A"
d"
g"
B"
g
x
d
d'
B'
g'
A'
g1'
Рис. 7.9
Московский государственный
технический университет
им. Н.Э. Баумана
Рис. 7.11
16.
Коническая поверхностьS
g"
S"
A"
g
d"
B"
x
B'
d
A'
g'
d'
Рис. 7.10
Московский государственный
технический университет
им. Н.Э. Баумана
S'
Рис. 7.12
17.
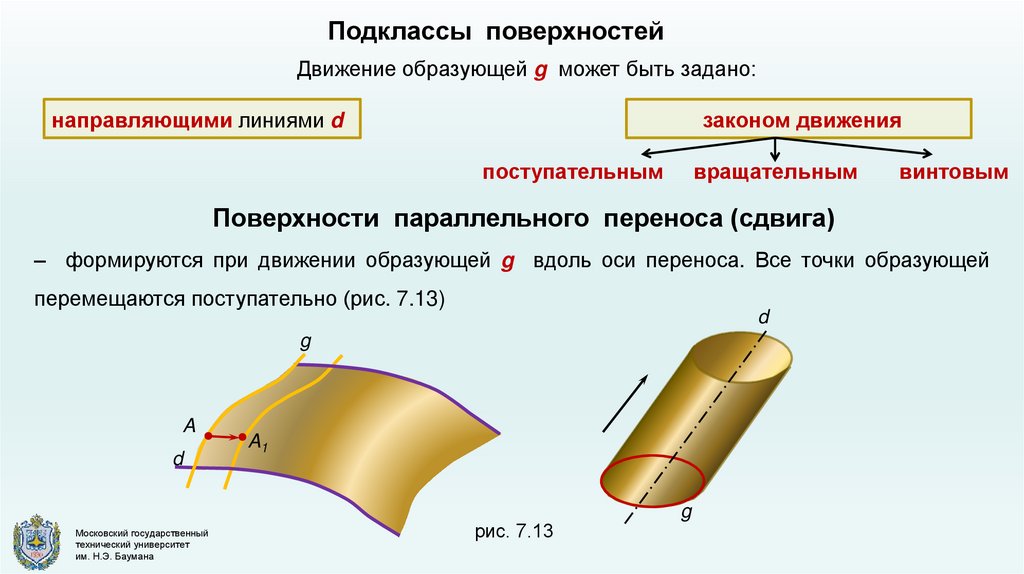
Подклассы поверхностейДвижение образующей g может быть задано:
направляющими линиями d
законом движения
поступательным
вращательным
винтовым
Поверхности параллельного переноса (сдвига)
– формируются при движении образующей g вдоль оси переноса. Все точки образующей
перемещаются поступательно (рис. 7.13)
d
g
A
d
Московский государственный
технический университет
им. Н.Э. Баумана
A1
рис. 7.13
g
18.
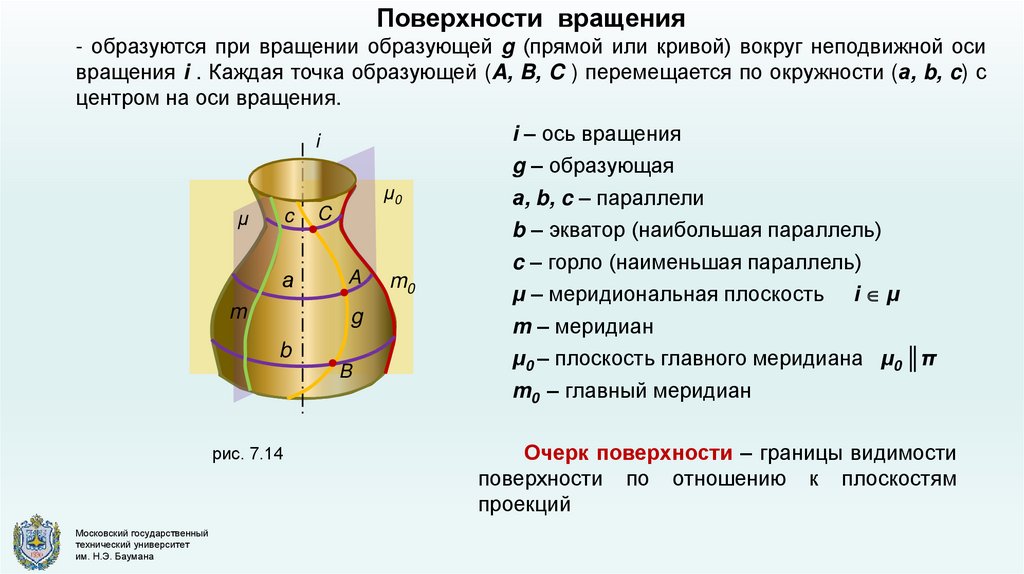
Поверхности вращения- образуются при вращении образующей g (прямой или кривой) вокруг неподвижной оси
вращения i . Каждая точка образующей (A, B, C ) перемещается по окружности (а, b, c) с
центром на оси вращения.
i
μ
c
а
m
μ0
C
A
g
b
B
рис. 7.14
Московский государственный
технический университет
им. Н.Э. Баумана
m0
i – ось вращения
g – образующая
а, b, c – параллели
b – экватор (наибольшая параллель)
c – горло (наименьшая параллель)
μ – меридиональная плоскость i μ
m – меридиан
μ0 – плоскость главного меридиана μ0 ║π
m0 – главный меридиан
Очерк поверхности – границы видимости
поверхности по отношению к плоскостям
проекций
19.
i"f0α
а"
A"
g"
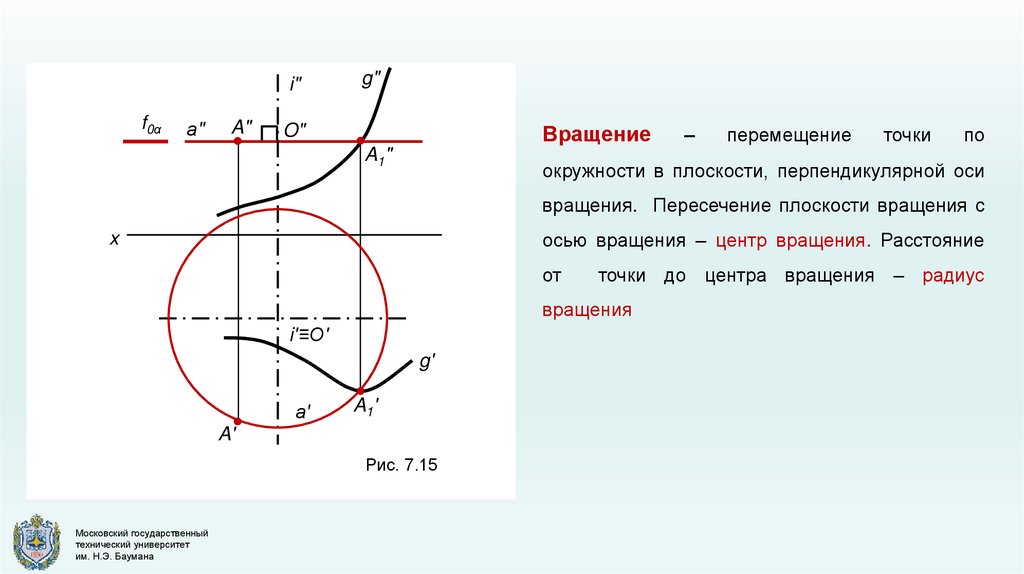
Вращение
O"
A1"
–
перемещение
точки
по
окружности в плоскости, перпендикулярной оси
вращения. Пересечение плоскости вращения с
осью вращения – центр вращения. Расстояние
x
от
точки до центра вращения – радиус
вращения
i'≡O'
g'
а'
A1'
A'
Рис. 7.15
Московский государственный
технический университет
им. Н.Э. Баумана
20.
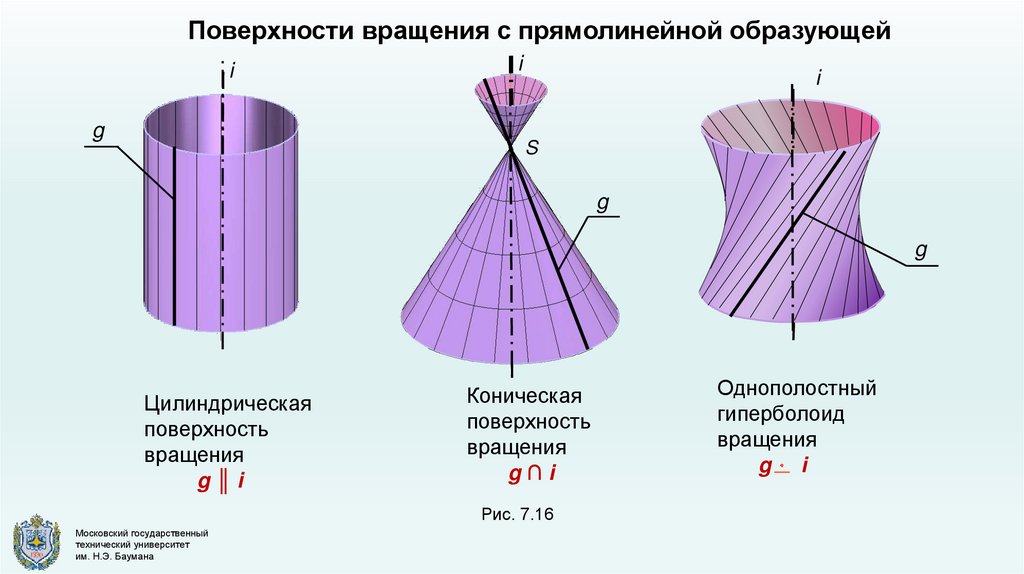
Поверхности вращения с прямолинейной образующейi
g
i
i
S
g
g
Цилиндрическая
поверхность
вращения
g║i
Коническая
поверхность
вращения
g∩i
Рис. 7.16
Московский государственный
технический университет
им. Н.Э. Баумана
Однополостный
гиперболоид
вращения
g i
21.
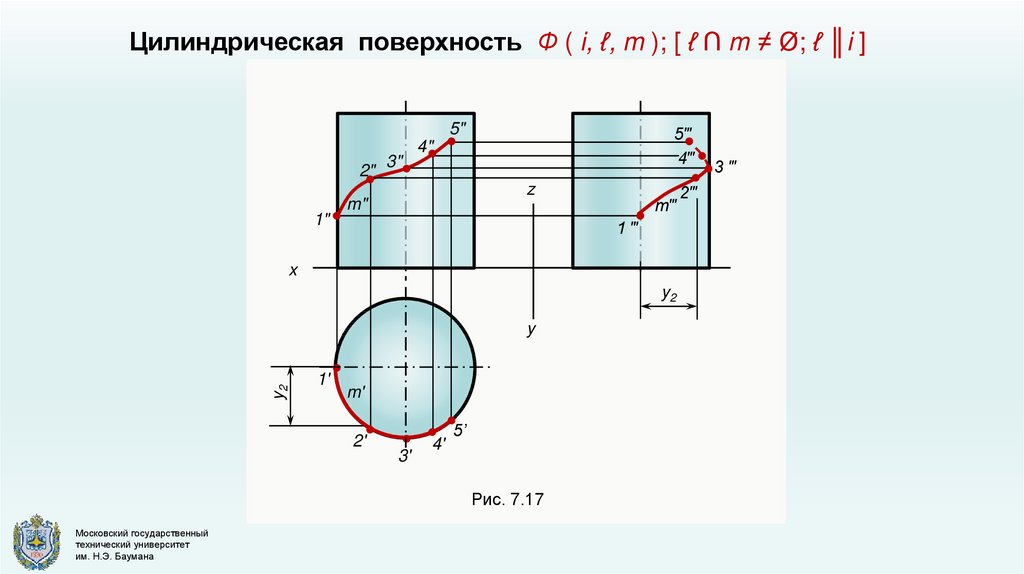
Цилиндрическая поверхность Ф ( i, ℓ, m ); [ ℓ ∩ m ≠ Ø; ℓ ║i ]5"
2"
1"
3"
5‴
4‴
4"
z
m"
m‴
1‴
x
y2
y2
y
1'
m'
2'
3'
4'
5’
Рис. 7.17
Московский государственный
технический университет
им. Н.Э. Баумана
2‴
3‴
22.
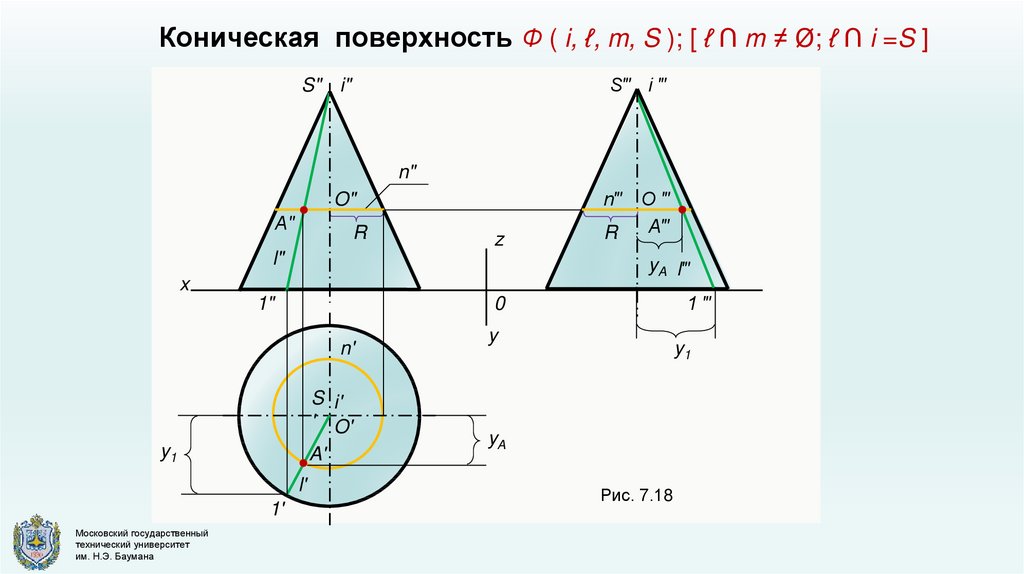
Коническая поверхность Ф ( i, ℓ, m, S ); [ ℓ ∩ m ≠ Ø; ℓ ∩ i =S ]S‴ i ‴
S" i"
n"
n‴
O"
А"
R
z
l"
yA l‴
x
1"
S i'
' O'
A'
y1
l'
Московский государственный
технический университет
им. Н.Э. Баумана
1‴
0
n'
1'
R
O‴
A‴
y
y1
yA
Рис. 7.18
23.
Поверхности вращения с образующей окружностьюi1
i4
i3
i2
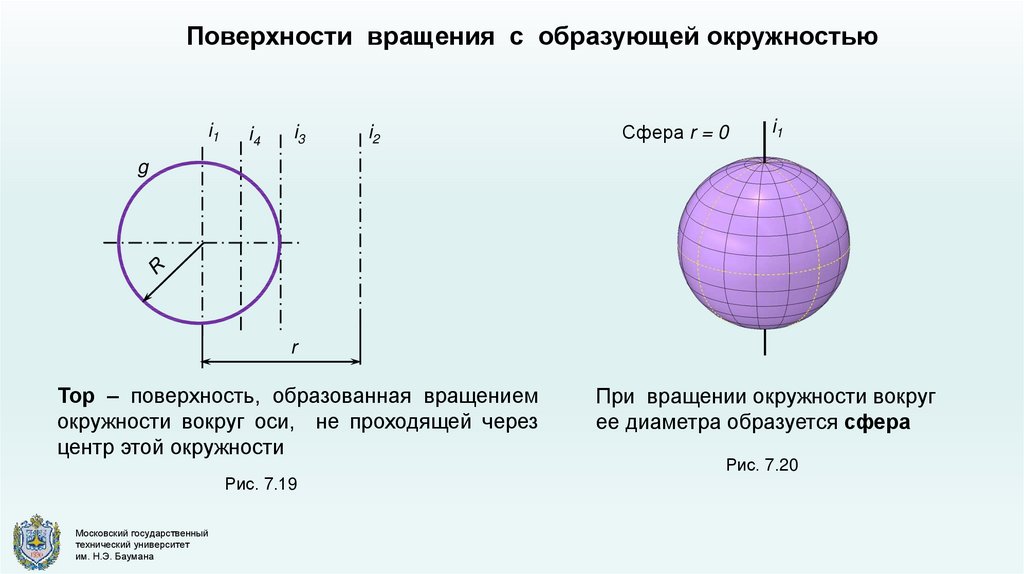
Сфера r = 0
i1
g
r
Тор – поверхность, образованная вращением
окружности вокруг оси, не проходящей через
центр этой окружности
Рис. 7.19
Московский государственный
технический университет
им. Н.Э. Баумана
При вращении окружности вокруг
ее диаметра образуется сфера
Рис. 7.20
24.
Торовые поверхностиОткрытый тор
Закрытый тор
r > R
r=R
Московский государственный
технический университет
им. Н.Э. Баумана
Рис. 7.21
Самопересекающийся тор
r< R
25.
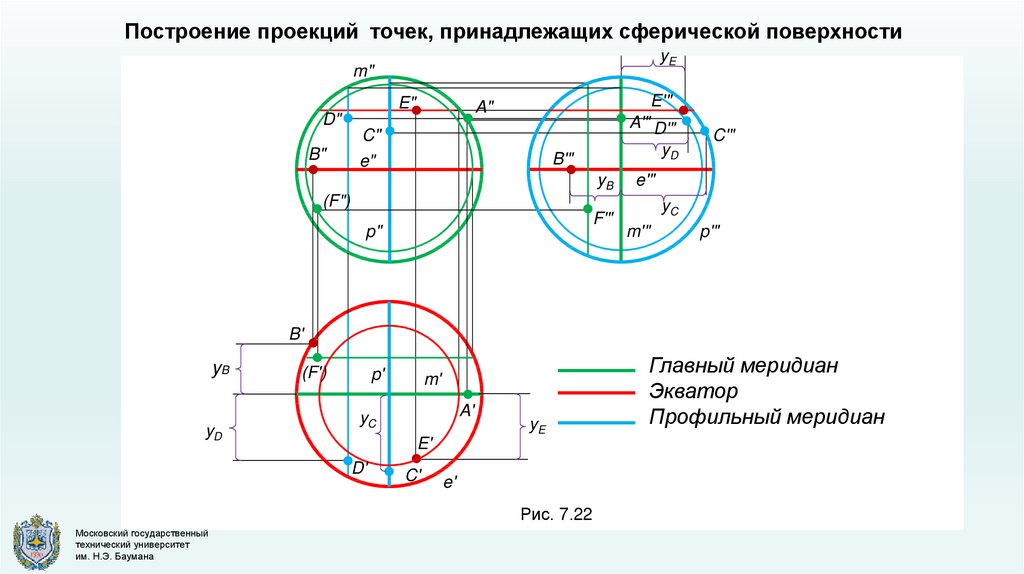
Построение проекций точек, принадлежащих сферической поверхностиyE
m"
E"
D"
B"
E'"
A"
A'" D'"
C"
yD
B'"
e"
yB
e'"
(F")
F'"
p"
C'"
yC
m'"
p'"
B'
yB
yD
(F')
p'
m'
A'
yC
yE
E'
D'
C'
e'
Рис. 7.22
Московский государственный
технический университет
им. Н.Э. Баумана
Главный меридиан
Экватор
Профильный меридиан
26.
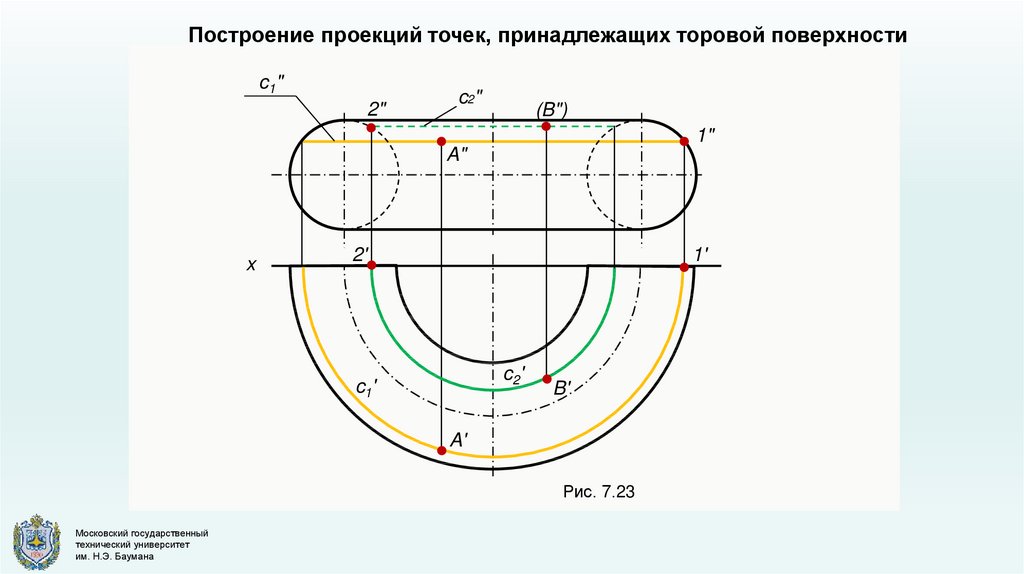
Построение проекций точек, принадлежащих торовой поверхностиc1"
2"
c2"
(B")
1"
A"
x
2'
1'
c2'
c1'
B'
A'
Рис. 7.23
Московский государственный
технический университет
им. Н.Э. Баумана
27.
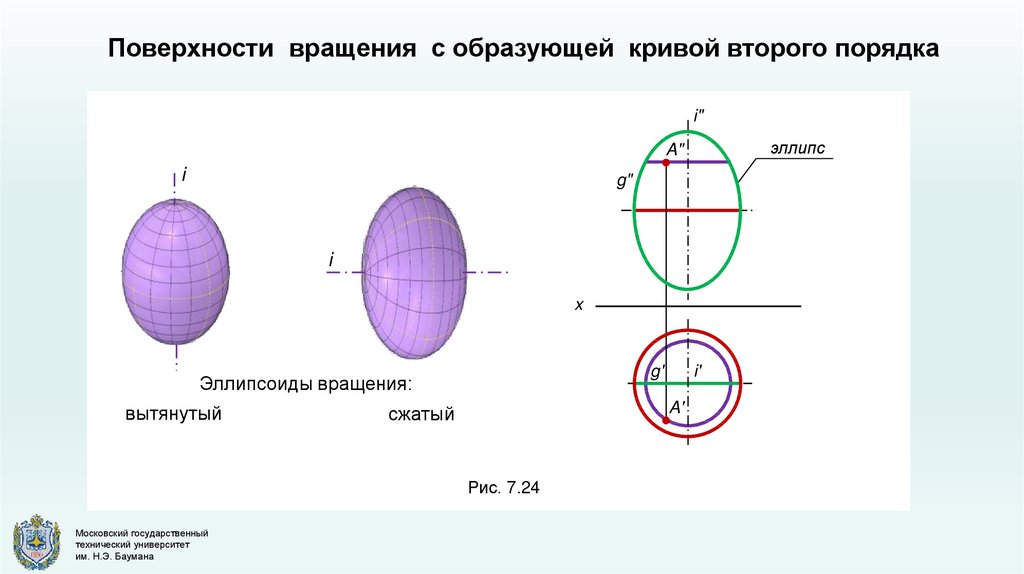
Поверхности вращения с образующей кривой второго порядкаi"
эллипс
A"
i
g"
i
x
g'
Эллипсоиды вращения:
вытянутый
A'
сжатый
Рис. 7.24
Московский государственный
технический университет
им. Н.Э. Баумана
i'
28.
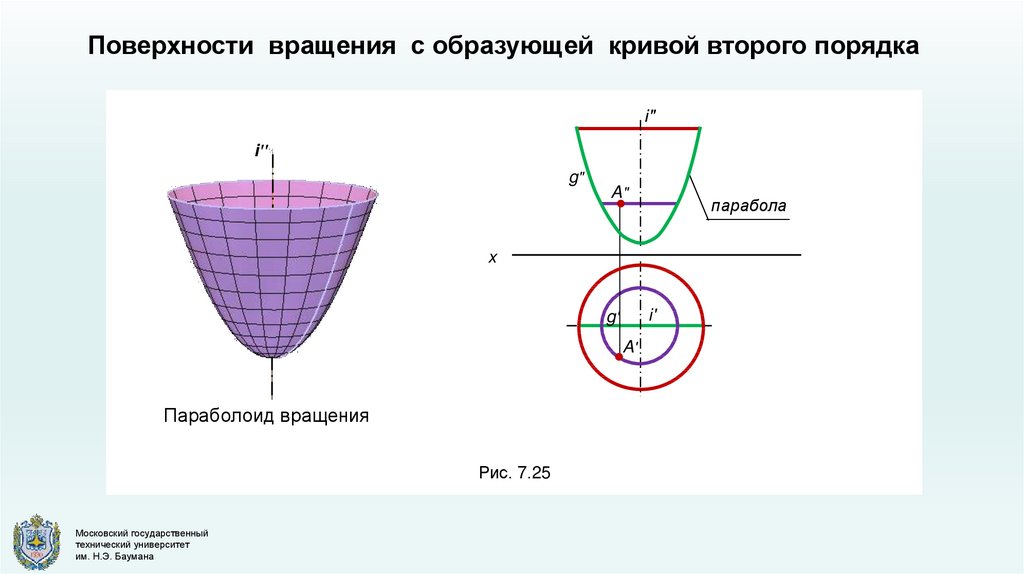
Поверхности вращения с образующей кривой второго порядкаi"
i"
g"
A"
парабола
x
i'
g'
A'
Параболоид вращения
Рис. 7.25
Московский государственный
технический университет
им. Н.Э. Баумана
29.
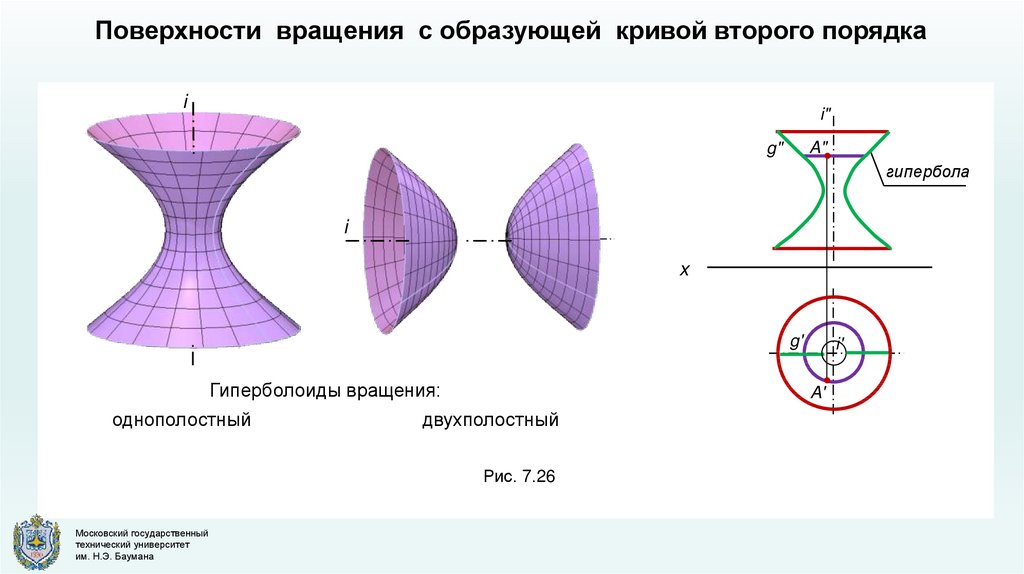
Поверхности вращения с образующей кривой второго порядкаi
i"
A"
g"
гипербола
i
x
g'
Гиперболоиды вращения:
однополостный
A'
двухполостный
Рис. 7.26
Московский государственный
технический университет
им. Н.Э. Баумана
i'
30.
Винтовые поверхностиВинтовая поверхность формируется при винтовом движении образующей (прямой или кривой)
вокруг оси.
Винтовое движение – совокупность двух перемещений: поступательного вдоль некоторой оси и
вращательного вокруг той же оси.
Шаг (P) винтовой поверхности – перемещение образующей вдоль оси за один оборот
g
i
i
g
Линейчатая
винтовая поверхность
Московский государственный
технический университет
им. Н.Э. Баумана
Трубчатая
винтовая поверхность
Рис. 7.27
31.
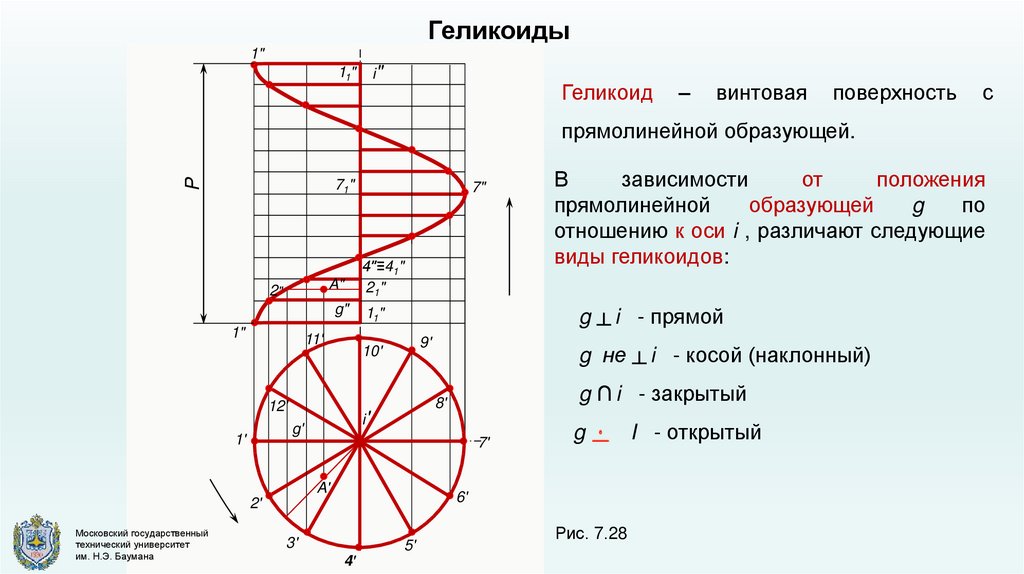
Геликоиды1"
i"
11"
Геликоид
–
винтовая
поверхность
с
P
прямолинейной образующей.
71"
A"
2"
g"
1"
11'
4"≡41"
21"
9'
7'
A'
g
6'
2'
Московский государственный
технический университет
им. Н.Э. Баумана
g не ┴ i - косой (наклонный)
g ∩ i - закрытый
8'
i'
g'
В
зависимости
от
положения
прямолинейной
образующей
g
по
отношению к оси i , различают следующие
виды геликоидов:
g ┴ i - прямой
11"
10'
12'
1'
7"
3'
5'
4'
Рис. 7.28
I - открытый







 drafting
drafting








