Similar presentations:
Поверхности. Способы задания поверхности
1. Поверхности
12.
Поверхность – непрерывноедвумерное множество точек.
Измерения : длина, ширина,
площадь. Толщины и объема
нет.
2
3.
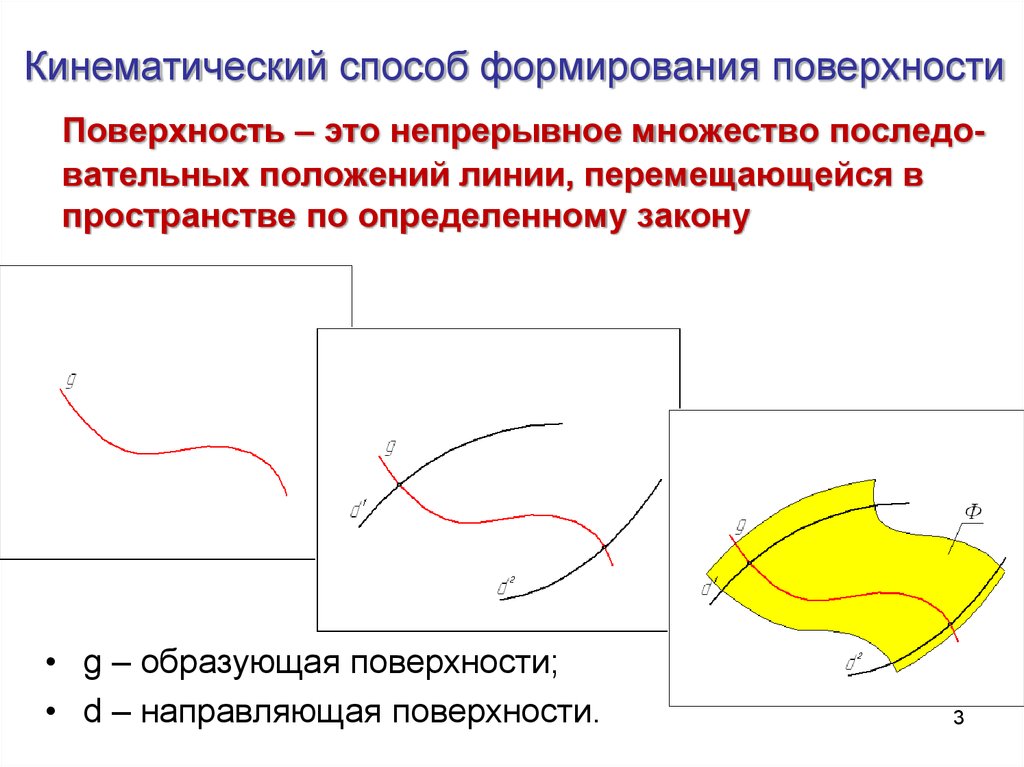
Кинематический способ формирования поверхностиПоверхность – это непрерывное множество последовательных положений линии, перемещающейся в
пространстве по определенному закону
• g – образующая поверхности;
• d – направляющая поверхности.
3
4. Способы задания поверхности
45. Определитель поверхности
Это совокупность независимых условий, однозначнозадающих поверхность.
Определитель состоит из двух частей:
Ф{(Г)(А)}
•Геометрическая (Г) - геометрические фигуры - образующая и
другие точки, линии, поверхности, участвующие в образовании поверхности.
•Алгоритмическая (А) – закон перемещения и изменения
формы образующей.
Если образующая является прямой линией, которую можно
однозначно задать двумя точками или точкой и направлением
и графически не изображать, в отличие от кривой линии, то ее
обозначение выносят за пределы геометрической части
определителя
Ф{g(Г)(А)}
5
6.
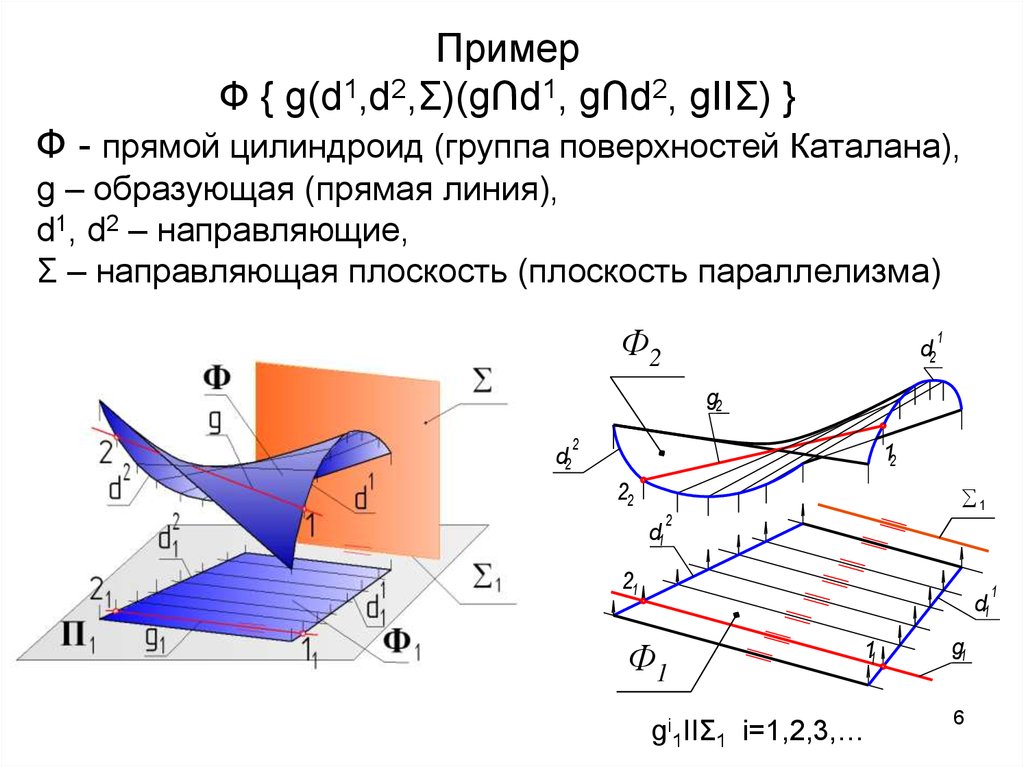
ПримерФ { g(d1,d2,Σ)(g∩d1, g∩d2, gIIΣ) }
Ф - прямой цилиндроид (группа поверхностей Каталана),
g – образующая (прямая линия),
d1, d2 – направляющие,
Σ – направляющая плоскость (плоскость параллелизма)
Ф2
d2
1
g2
d2
2
12
1
22
d1
2
21
d1
Ф1
11
gi1IIΣ1 i=1,2,3,…
g1
6
1
7. Каркас поверхности
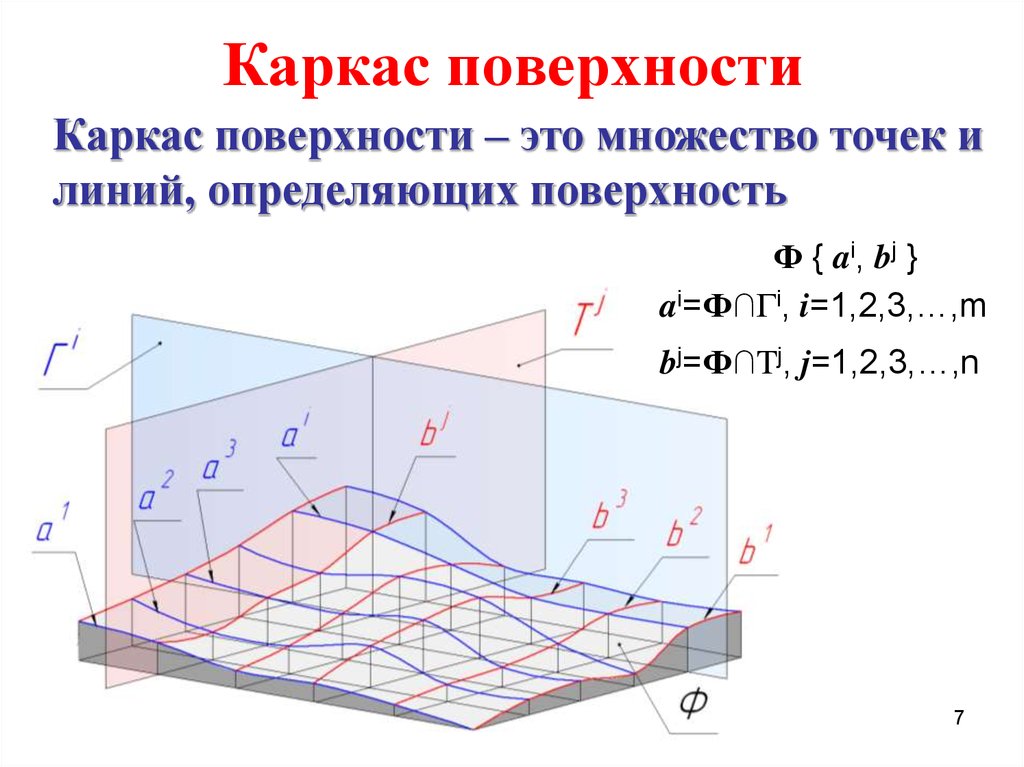
Каркас поверхности – это множество точек илиний, определяющих поверхность
Ф { ai, bj }
ai=Ф∩Гi, i=1,2,3,…,m
bj=Ф∩Tj, j=1,2,3,…,n
7
8. Очерк поверхности
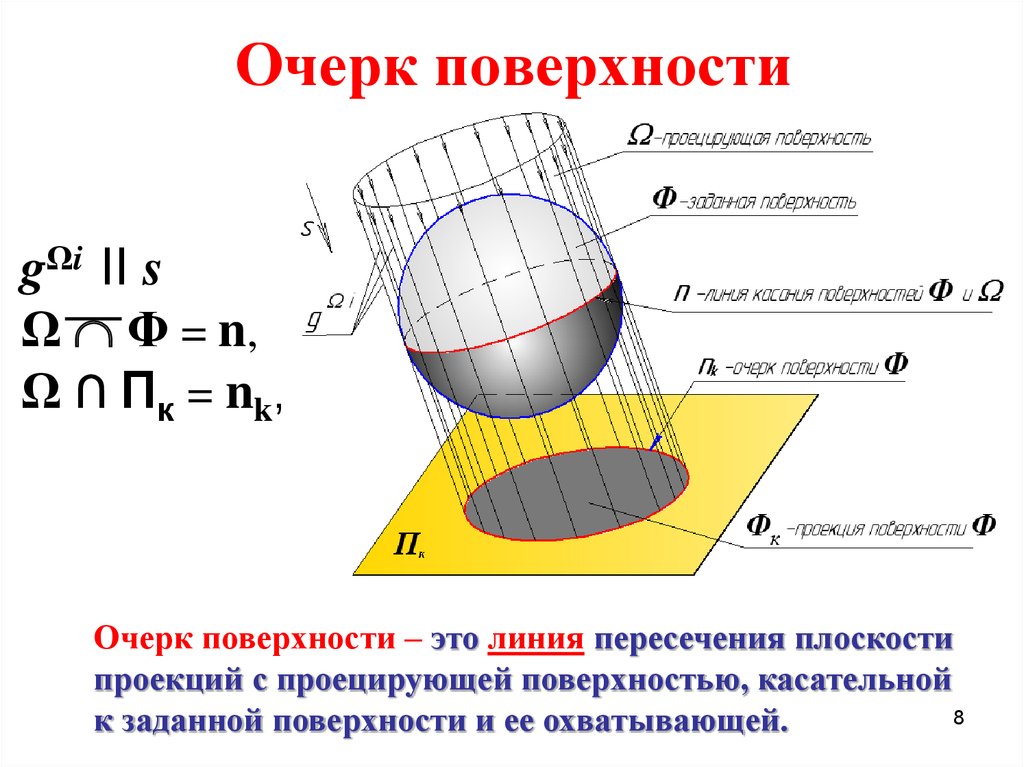
gΩi II sΩ Φ = n,
Ω ∩ П к = nk ,
Очерк поверхности – это линия пересечения плоскости
проекций с проецирующей поверхностью, касательной
8
к заданной поверхности и ее охватывающей.
9.
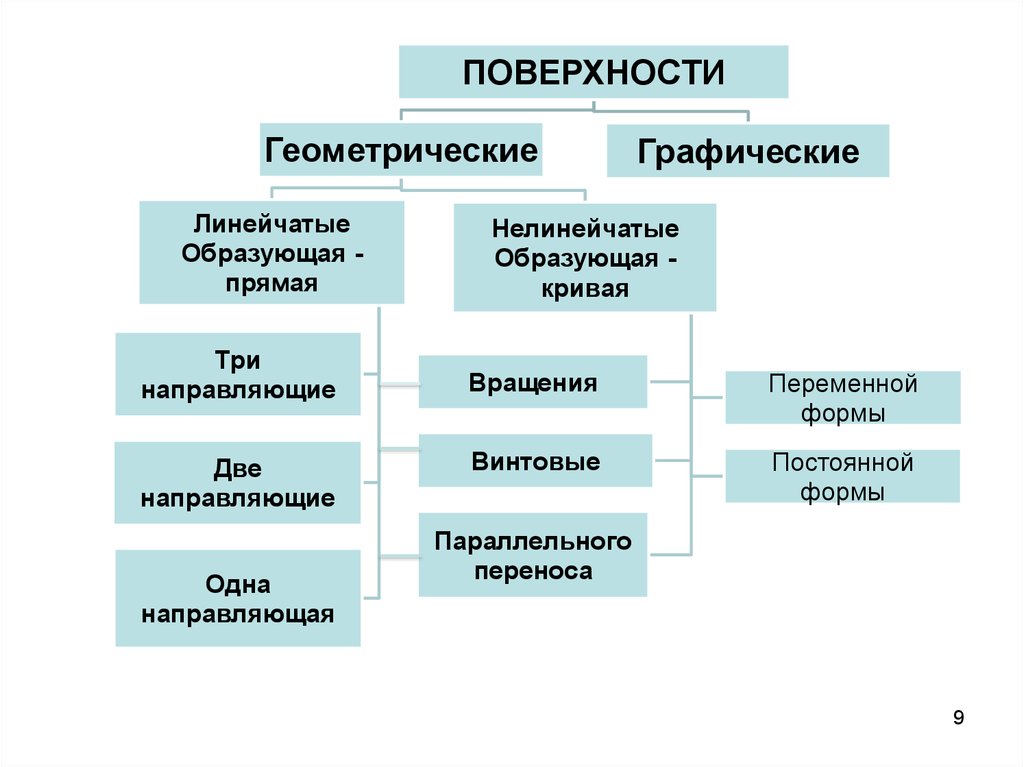
ПОВЕРХНОСТИГеометрические
Линейчатые
Образующая прямая
Три
направляющие
Две
направляющие
Одна
направляющая
Графические
Нелинейчатые
Образующая кривая
Вращения
Переменной
формы
Винтовые
Постоянной
формы
Параллельного
переноса
9
10. Геометрическая поверхность
Графическаяповерхность
10
11. Геометрические поверхности
1112. Линейчатые поверхности Образующая поверхности – прямая линия
1213. С тремя направляющими
Ф{g(d1,d2,d3)(g∩d1, g∩d2, g∩d3)}Поверхность
косого клина
Поверхность
косого перехода
13
14.
С двумя направляющими и направляющей плоскостьюили плоскостью параллелизма (поверхности Каталана)
Ф{g(d1,d2, )(g∩d1, g∩d2,gII )}
Ф{g(d1,d2, )(g∩d1, g∩d2, =(g^ )=const)}
Гиперболический
параболоид
14
15. С одной направляющей Торсы
Ф{g(d,S)(g∩d,S g)}S – реальная точка
S∞ - несобственная точка пространства
Ф{g(d,s)(g∩d, g II s)}
15
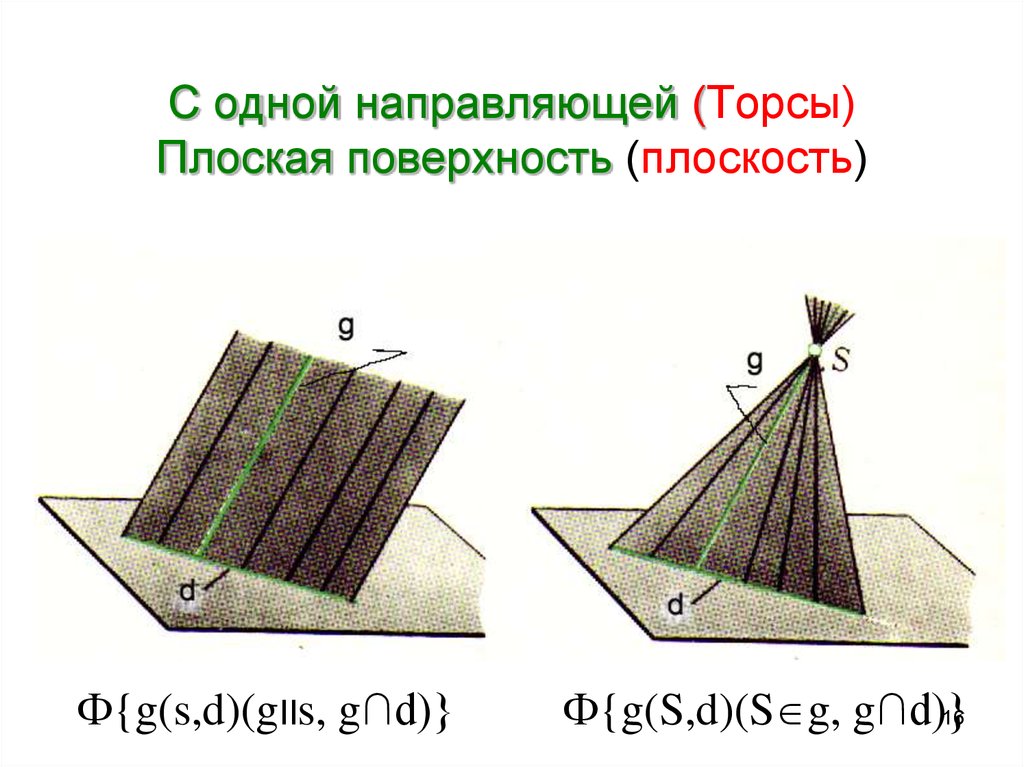
16. С одной направляющей (Торсы) Плоская поверхность (плоскость)
Ф{g(s,d)(gIIs, g∩d)}Ф{g(S,d)(S g, g∩d)}
16
17. Гранные поверхности
ПирамидальнаяПризматическая
17
18. Поверхности вращения
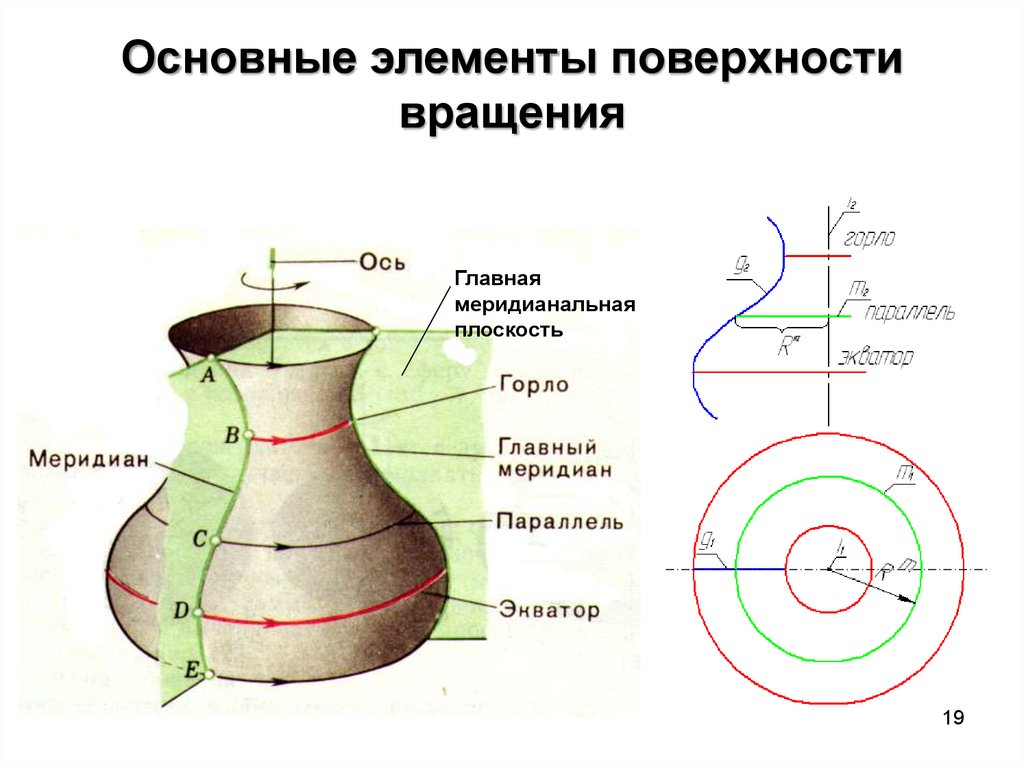
1819. Основные элементы поверхности вращения
Главнаямеридианальная
плоскость
19
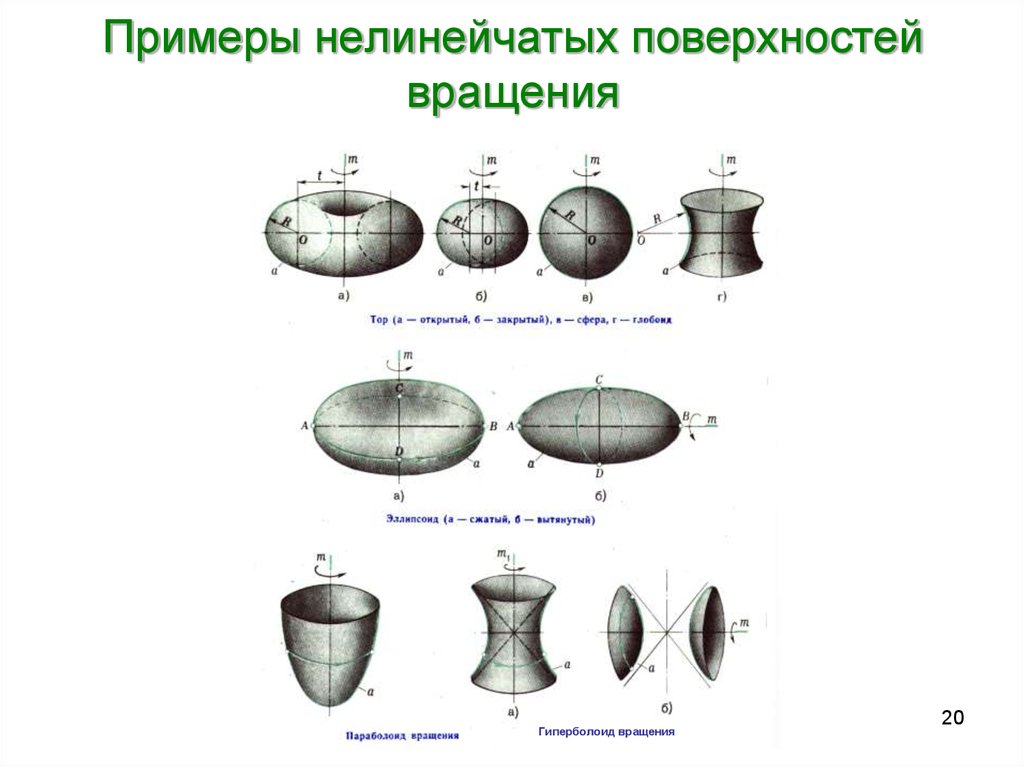
20. Примеры нелинейчатых поверхностей вращения
Гиперболоид вращения20
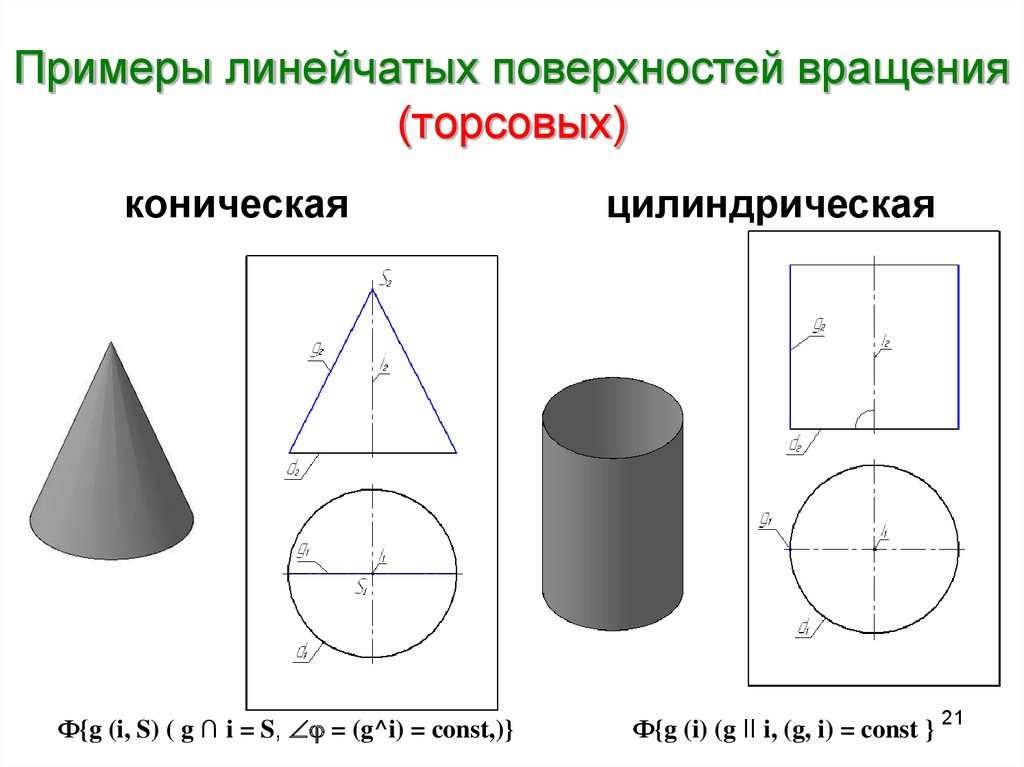
21. Примеры линейчатых поверхностей вращения (торсовых)
коническаяФ{g (i, S) ( g ∩ i = S, = (g^i) = const,)}
цилиндрическая
Ф{g (i) (g II i, (g, i) = const } 21
22. Винтовые поверхности
2223.
Ф{g(d1,d2)(g∩d1,g∩d2,(g^d2)=const)}23
24. Поверхности параллельного переноса
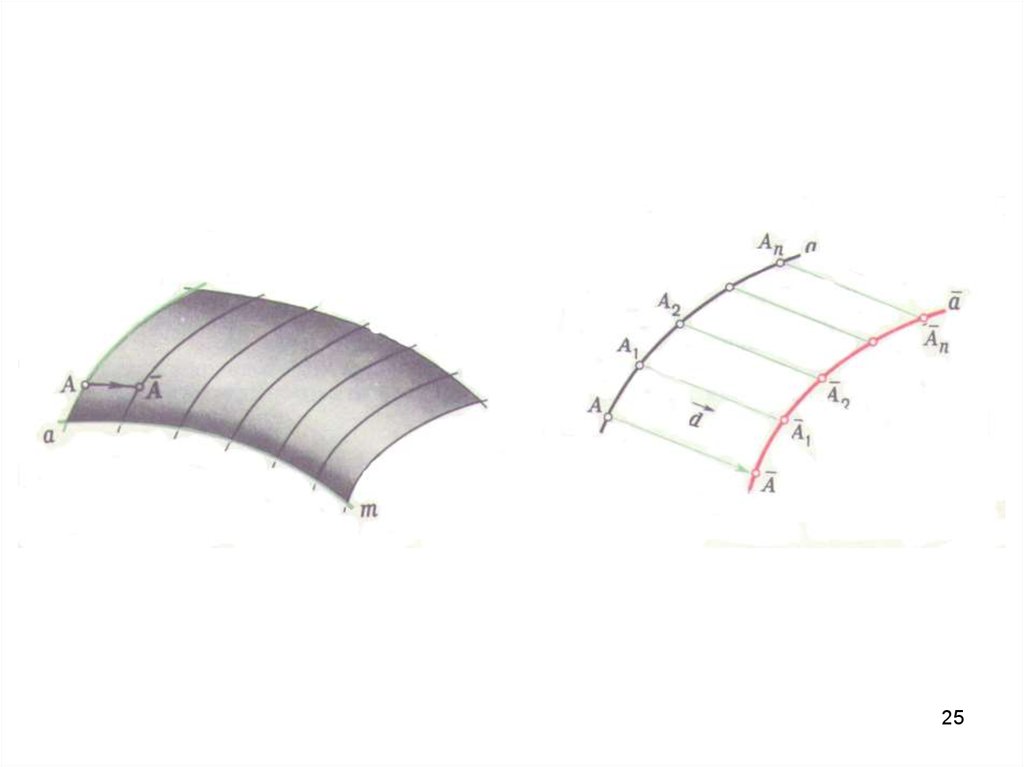
2425.
2526. Примеры современных архитектурных форм
2627. Обобщенные позиционные задачи
2728. Точка на поверхности
2829.
Точка принадлежит поверхности,если она принадлежит линии,
принадлежащей этой поверхности
А Ф А l , l Ф
Линия l должна на проекциях иметь наиболее
простую геометрическую форму: прямой
или окружности (по возможности)
29
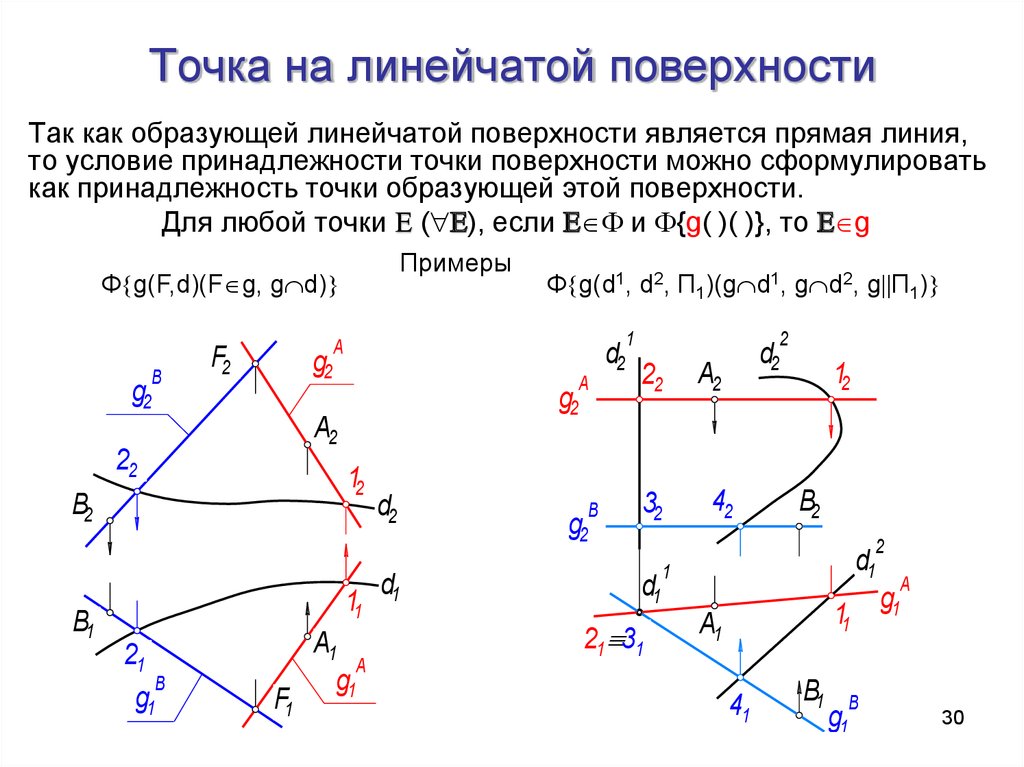
30. Точка на линейчатой поверхности
Так как образующей линейчатой поверхности является прямая линия,то условие принадлежности точки поверхности можно сформулировать
как принадлежность точки образующей этой поверхности.
Для любой точки ( ), если и {g( )( )}, то g
Примеры
Ф g(F,d)(F g, g d)
g2
B
F2
g2
A
d2
g2
A2
22
12
B2
11
B1
21
B
g1
F1
Ф g(d1, d2, П1)(g d1, g d2, g П1)
A1
A
g1
d2
d1
A
g2
B
1
22
32
d1
21 31
d2
A2
42
2
12
B2
d1
1
11
A1
41
B1
g1
B
2
g1
A
30
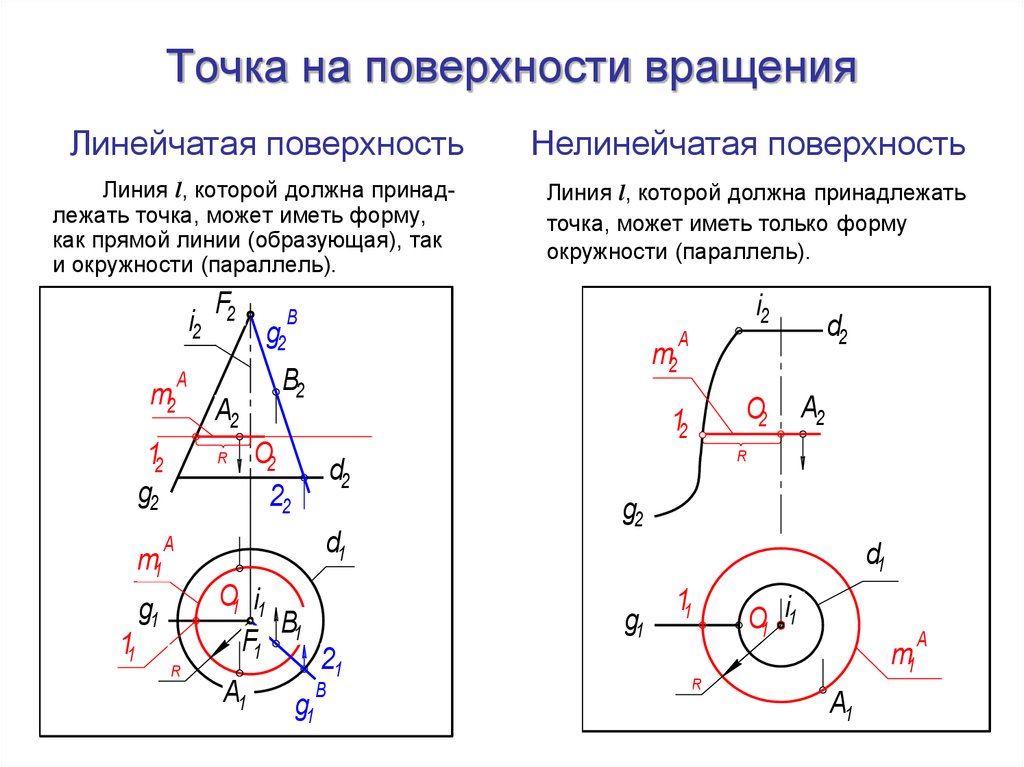
31. Точка на поверхности вращения
Линейчатая поверхностьЛиния l, которой должна принадлежать точка, может иметь форму,
как прямой линии (образующая), так
и окружности (параллель).
i2
m2
A
12
g2
m1
11
F2
A2
R
g2
i2
m2
B2
O2
22
A1
O2
g1
g2
d1
g1
21
B
A2
R
d2
d1
d2
A
12
O1 i1
B
F1 1
R
Линия l, которой должна принадлежать
точка, может иметь только форму
окружности (параллель).
B
A
g1
Нелинейчатая поверхность
11
O1 i1
m1
R
A1
A
31
32. Линия на поверхности
33.
• Линия принадлежит поверхности, есливсе множество ее точек принадлежит
этой поверхности.
• Следовательно, чтобы построить
линию на поверхности, необходимо
представить эту линию, как множество
точек, и построить каждую из точек
этого множества, используя условие
принадлежности точки поверхности.
34. Построение произвольной линии на поверхности
В качестве примера взята цилиндрическая поверхность общего видаФ{g(d,s)(g∩d, g II s)}
- линейчатая поверхность
Следовательно, для А l, точка g, g Ф
l l{1,2,3,…}
l{1,2,3,…}






















 drafting
drafting








