Поверхности. Задание поверхности на комплексном чертеже (лекция 7)

1. ЛЕКЦИЯ 7 Поверхности

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ
ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
"САМАРСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
УНИВЕРСИТЕТ ИМЕНИ АКАДЕМИКА С.П. КОРОЛЕВА»
(САМАРСКИЙ УНИВЕРСИТЕТ)
ЛЕКЦИЯ 7
Поверхности

2.

Определение и задание на
чертеже
Определение
Поверхность – совокупность всех последовательных
положений движущейся линии (образующей) в
пространстве (кинематическая поверхность)
Способы задания
1. Кинематический – как след движущейся линии
2. Аналитический – как множество точек,
удовлетворяющих функционалу: F(x,y,z)
3. Графический – задание поверхности на комплексном
чертеже.

3.

Задание поверхности на комплексном
чертеже
1. Определителем (набором элементов,
определяющих эту поверхность) –
совокупность геометрических элементов,
позволяющих реализовать закон образования
поверхности
2. Каркасом – называется множество точек
или линий, определяющих поверхность
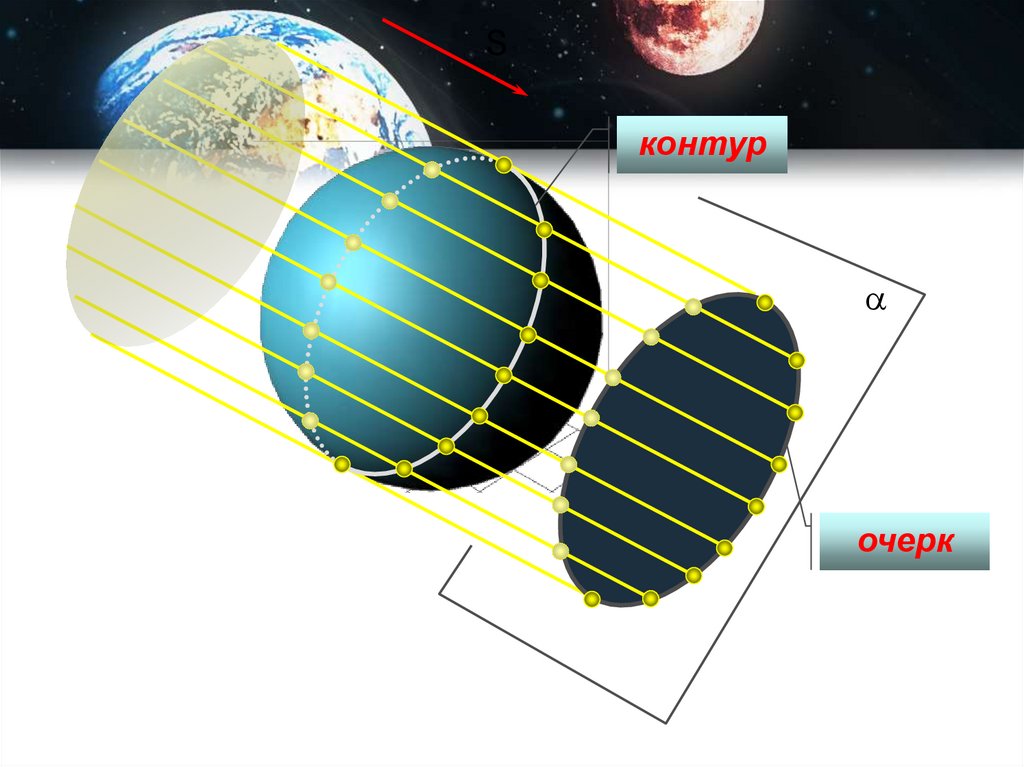
3. Очерком – называется проекции контура
поверхности на плоскости проекций

4.

S
контур
очерк

5.

6.

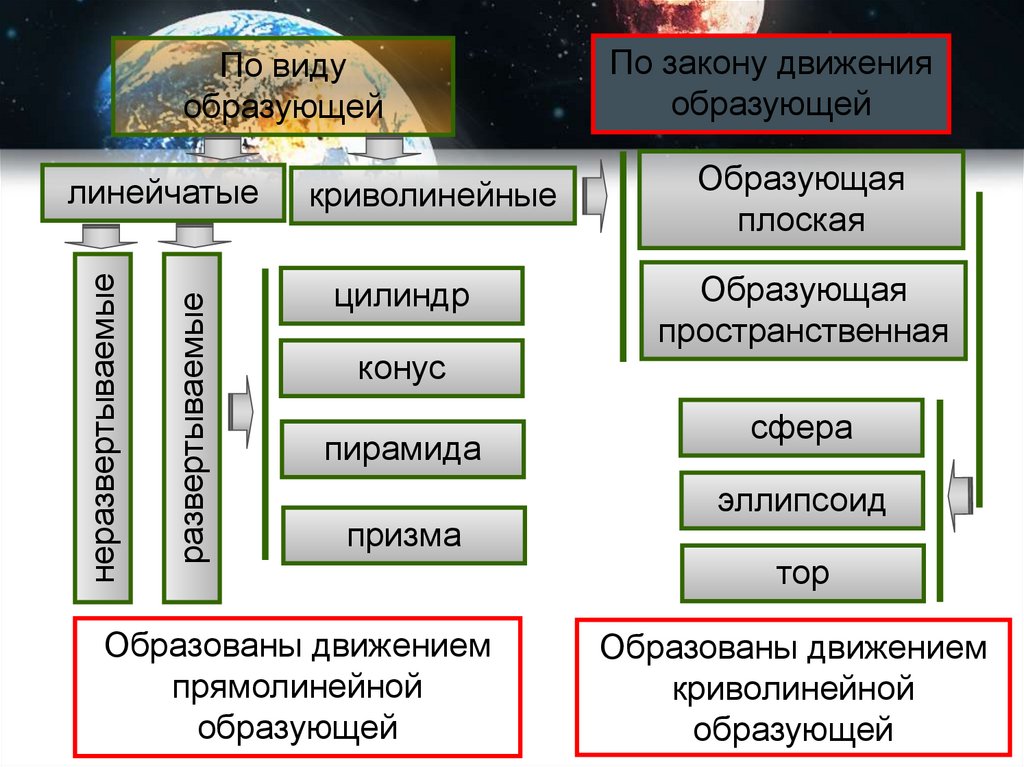
По виду
образующей
развертываемые
неразвертываемые
линейчатые
криволинейные
цилиндр
конус
пирамида
призма
Образованы движением
прямолинейной
образующей
По закону движения
образующей
Образующая
плоская
Образующая
пространственная
сфера
эллипсоид
тор
Образованы движением
криволинейной
образующей

7.

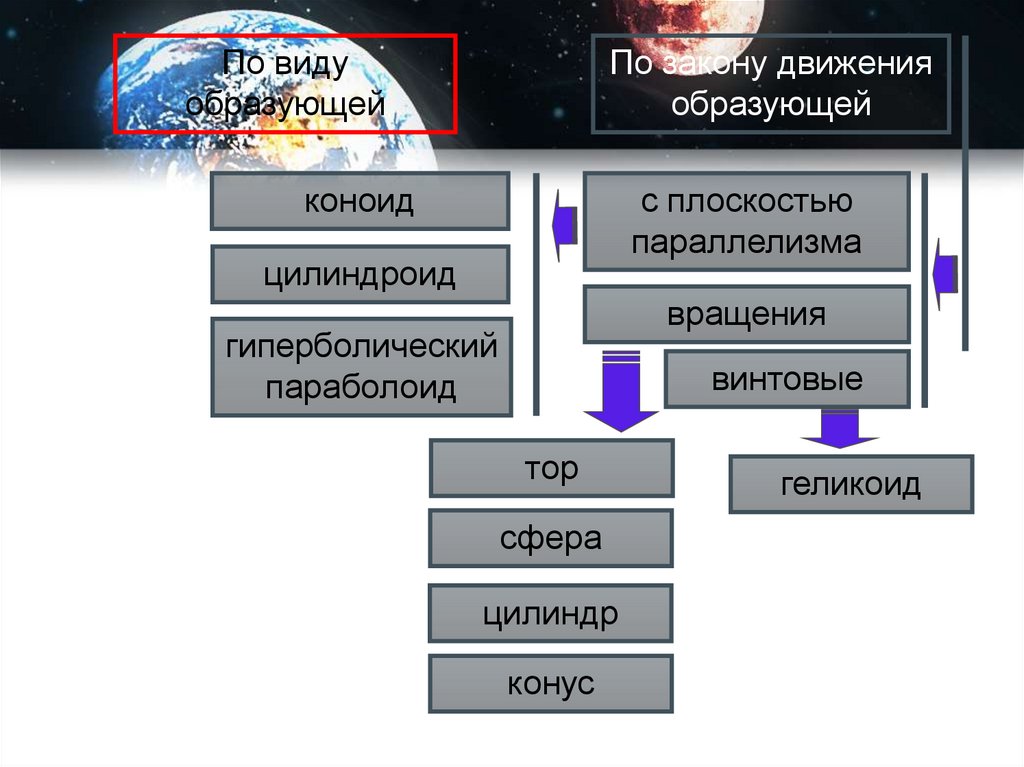
По виду
образующей
По закону движения
образующей
коноид
с плоскостью
параллелизма
цилиндроид
вращения
гиперболический
параболоид
винтовые
тор
сфера
цилиндр
конус
геликоид

8.

Кривые линии

9.

гипербола
С
А
В
Если в образовании кривой линии
наблюдается закономерность,
которая может быть выражена
уравнением в той
или иной системе координат,
то такая кривая называется
закономерной, например эллипс,
парабола, гипербола и др.
Незакономерной называется
кривая линия, в которой нельзя
обнаружить закономерности
образования, например линия
пересечения рельефа местности
плоскостью

10.

Линейчатые поверхности
Образование поверхностей

11.

Линейчатой поверхностью называется
поверхность, образованная перемещением
прямолинейной образующей по одной или более
направляющим
Любое тело ограничивается своей поверхностью.
Тело- конечно и состоит из конкретного
материала. Поверхность является абстрактной
фигурой, не имеющей толщины, это тонкая пленка
натянутая на каркас.
Например: шар-тело, сфера – поверхность.
На КЧ задаются проекцией этих элементов или
очерком.

12.

Цилиндрическая поверхность
Цилиндрическая поверхность
S
1
ℓ
m1
ℓi-1 m
2
ℓi+1
m2
образуется движением прямой ℓ
(образующей) по некоторой
кривой m параллельно самой себе
или имеющей постоянное
направление S
ℓ- образующая
m- направляющая
S- направление
В любой момент времени
соблюдается условие:
1)Образующая ℓ всегда параллельна
предыдущей образующей (ℓi-1ǁℓi+1)
2)Образующая должна пересекаться в
любой момент времени с двумя
направляющимися ℓi m1=1 ℓi m2=2

13.

Коническая поверхность
i
ℓ
S
∆(i, ℓ m; ℓ i )
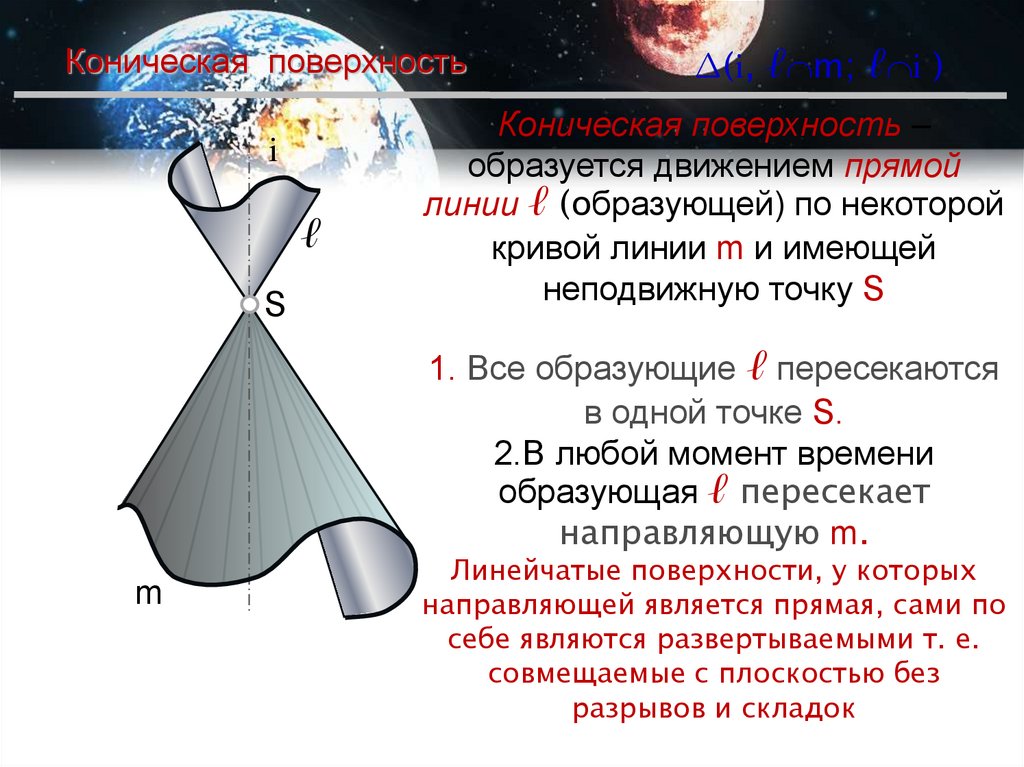
Коническая поверхность –
образуется движением прямой
линии ℓ (образующей) по некоторой
кривой линии m и имеющей
неподвижную точку S
1. Все образующие ℓ пересекаются
в одной точке S.
2.В любой момент времени
образующая ℓ пересекает
направляющую m.
m
Линейчатые поверхности, у которых
направляющей является прямая, сами по
себе являются развертываемыми т. е.
совмещаемые с плоскостью без
разрывов и складок

14.

Поверхности вращения

15.

Поверхность α , образованная вращением
образующей ℓ вокруг неподвижной оси i,
называется поверхностью вращения.
Они делятся на поверхности линейчатыеобразующая прямая линия и поверхности
нелинейчатые (криволинейные)-

16.

Поверхность вращения общего вида
i
i – ось вращения
g
i П1
g – образующая –
пространственная кривая
линия постоянного вида
– поверхность вращения

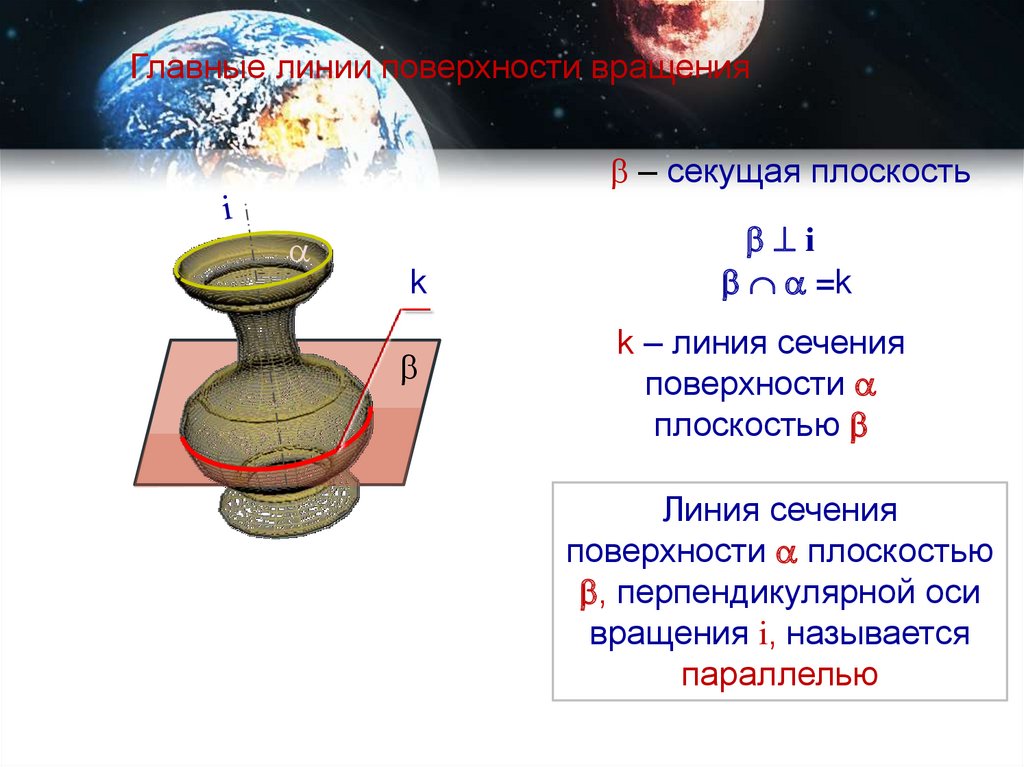
17.

Главные линии поверхности вращения
– секущая плоскость
k
i
=k
k – линия сечения
поверхности
плоскостью
Линия сечения
поверхности плоскостью
, перпендикулярной оси
вращения i, называется
параллелью

18.

экватор
горло
Параллель
с минимальным радиусом
называется горлом
горло
экват
ор
Параллель
с максимальным
радиусом называется
экватором

19.

m
λ – секущая плоскость
λ∈i
λ =m
m – линия сечения
поверхности
плоскостью λ
Линия сечения
поверхности плоскостью
λ, проходящей через ось
вращения i, называется
меридианом
(случайным меридианом)

20.

Главный
меридиан
меридиан
Пересечение поверхности
фронтальной плоскостью
уровня, проходящей через
ось вращения, образует
меридиан, который
называется главным
меридианом поверхности
и является очерком
фронтальной проекции
λ1гм
λ1
Главный меридиан
является границей
видимости

21.

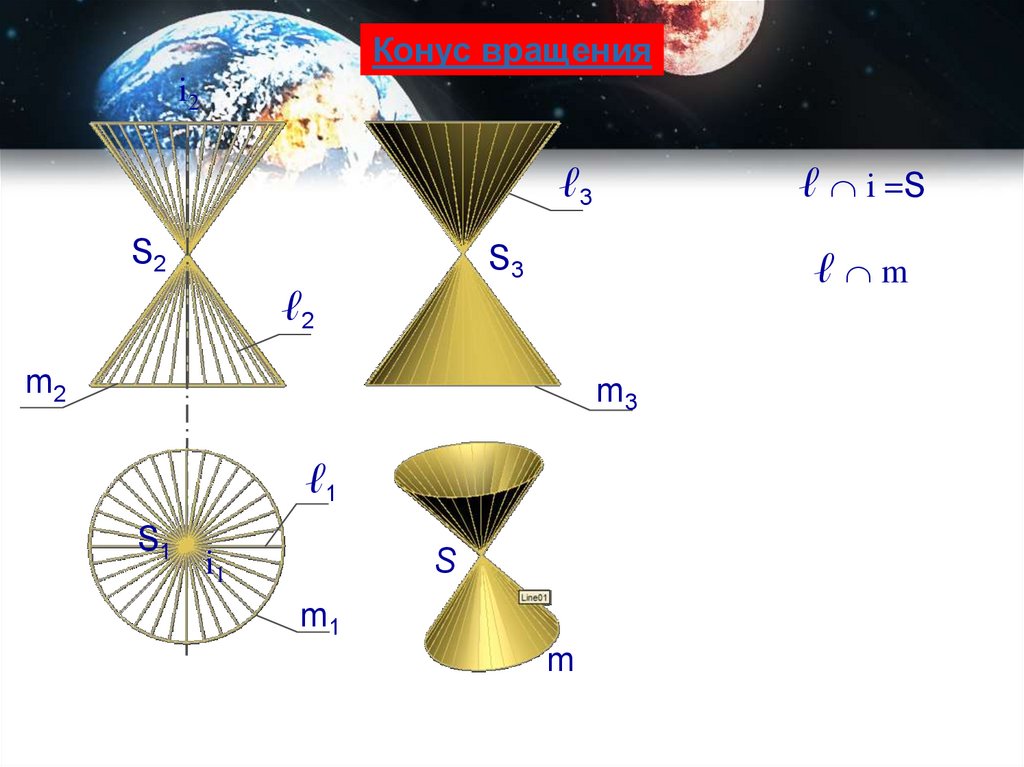
Конус вращения
i2
ℓ i =S
ℓ3
S2
ℓ m
S3
ℓ2
m2
m3
ℓ1
S1
S
i1
m1
m

22.

Принадлежность точки поверхности

23.

Точка принадлежит поверхности, если она
принадлежит линии, расположенной на этой
поверхности
Линия принадлежит поверхности, если
каждая ее точка принадлежит этой
поверхности

24.

Среди точек кривой выделяют опорные точки:
– экстремальные точки – высшая и низшая, крайняя
левая и крайняя правая, самая далекая и самая
ближняя точки кривой;
– граничные точки видимости кривой, принадлежащей
поверхности, лежат на очерках поверхности и
отделяют видимую часть поверхности от ее
невидимой части

25.

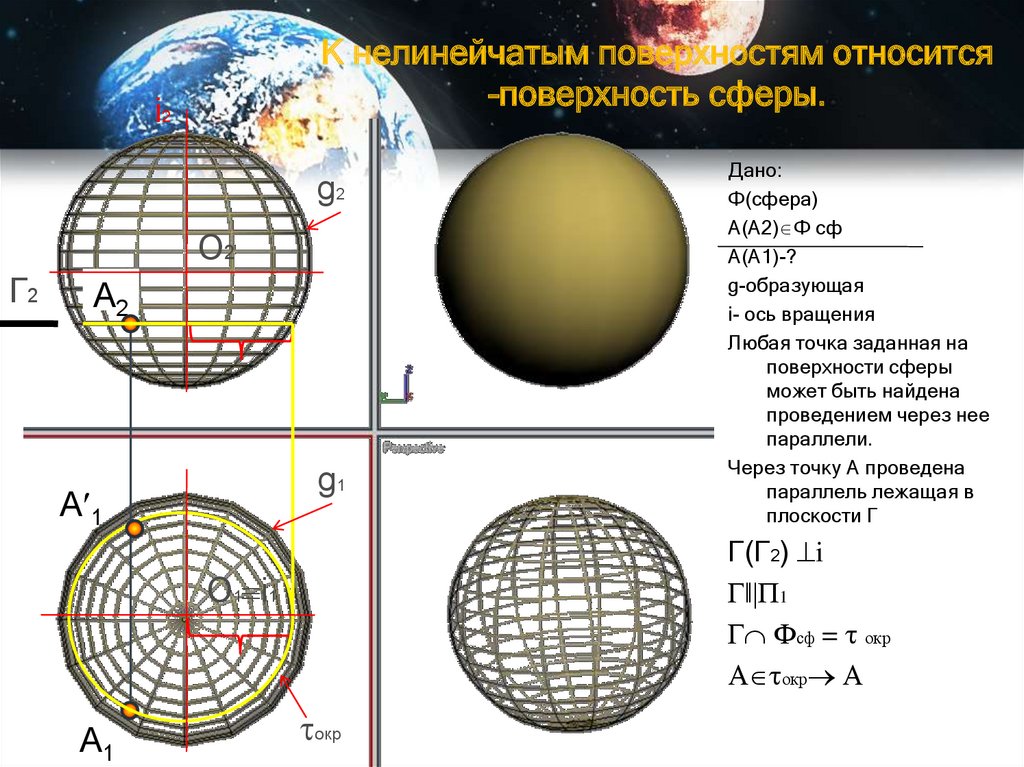
К нелинейчатым поверхностям относится
–поверхность сферы.
i2
g2
O2
Г2
A2
g1
A 1
Г(Г2) i
Гǁ|П1
Г Фсф = окр
А окр А
O1 i1
A1
Дано:
Ф(сфера)
А(А2) Ф сф
А(А1)-?
g-образующая
i- ось вращения
Любая точка заданная на
поверхности сферы
может быть найдена
проведением через нее
параллели.
Через точку А проведена
параллель лежащая в
плоскости Г
окр

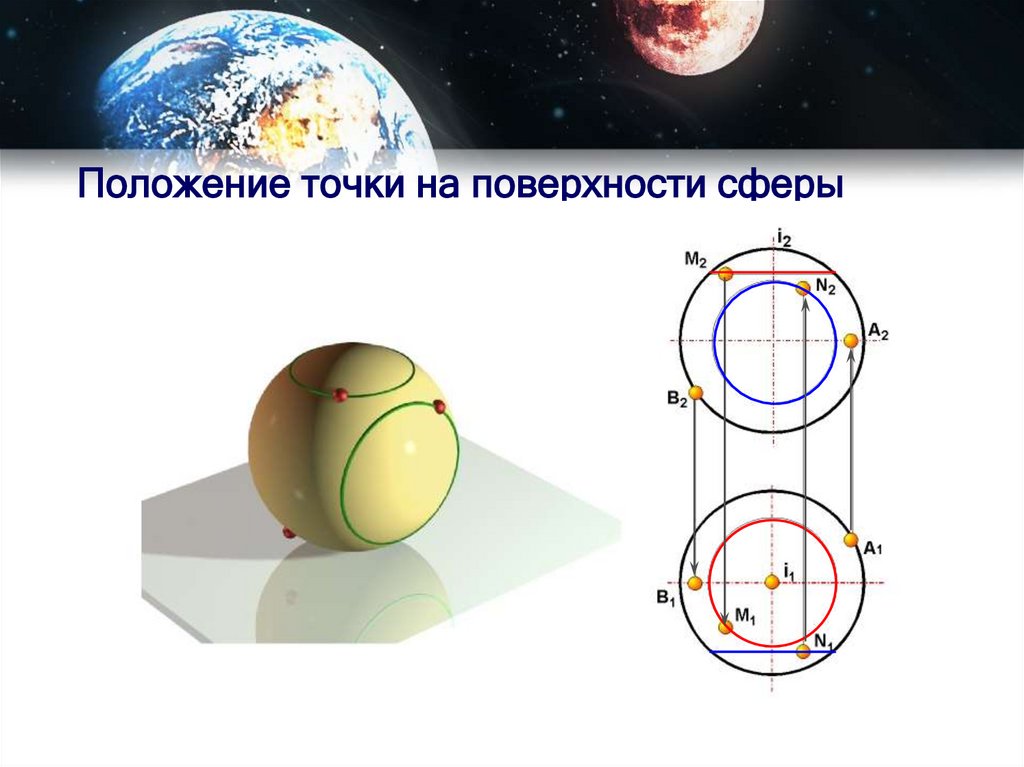
26. Положение точек на поверхности сферы

А2
А3
О3
О2
В2
В3
Главный фронтальный
меридиан
О1
Экватор
А1
В1
Профильный меридиан

27. Положение точки на поверхности сферы

28. Эллиптический цилиндр

12
22
А 1
2 1
21
Дано:
Фц
А(А2) Фц
А1-?
Через точку А на поверхности
цилиндра можно провести
образующую g и окружность,
причем окружность на плоскость
должна проецироваться без
искажения. В данном примере
возьмем образующую
проходящую через точку А.
Образующая пересекает
окружность верхнего и нижнего
основания в точках 1,2.
Недостающую проекцию точки
определяем по принадлежности к
направляющей. Задача имеет 2
решения (А1 и А 1)

29.

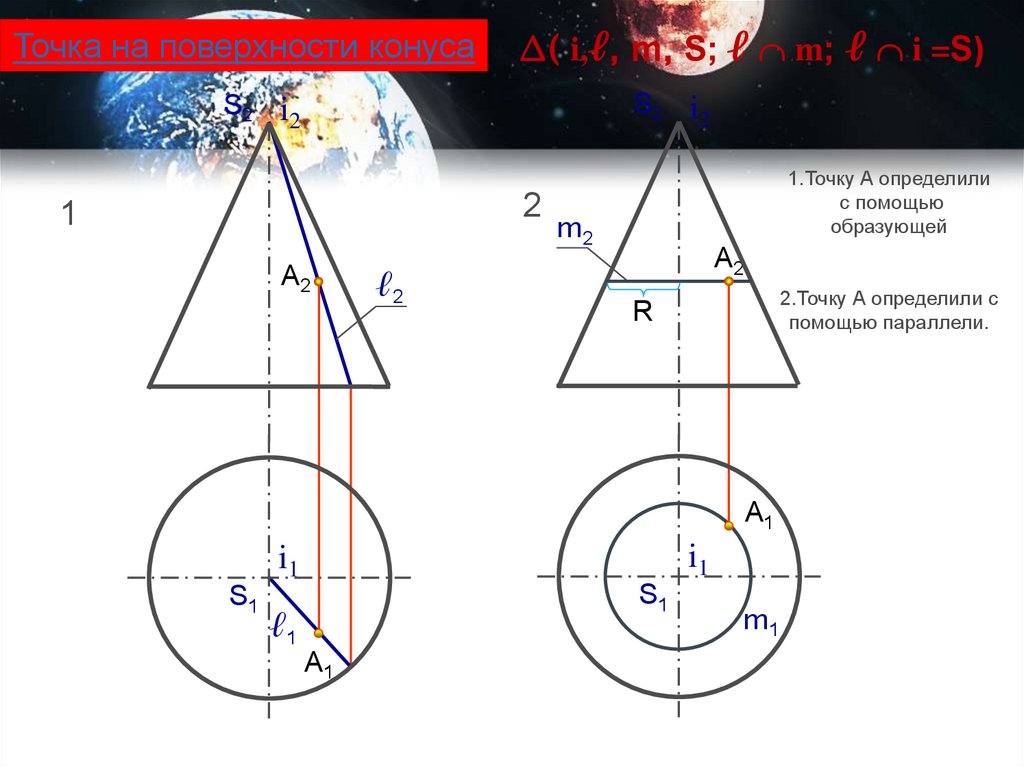
Точка на поверхности конуса
∆( i,ℓ, m, S; ℓ m; ℓ i =S)
S2 i2
S2 i2
2
1
А2
ℓ2
1.Точку А определили
с помощью
образующей
m2
А2
2.Точку А определили с
помощью параллели.
R
А1
i1
i1
S1
ℓ1
S1
А1
m1

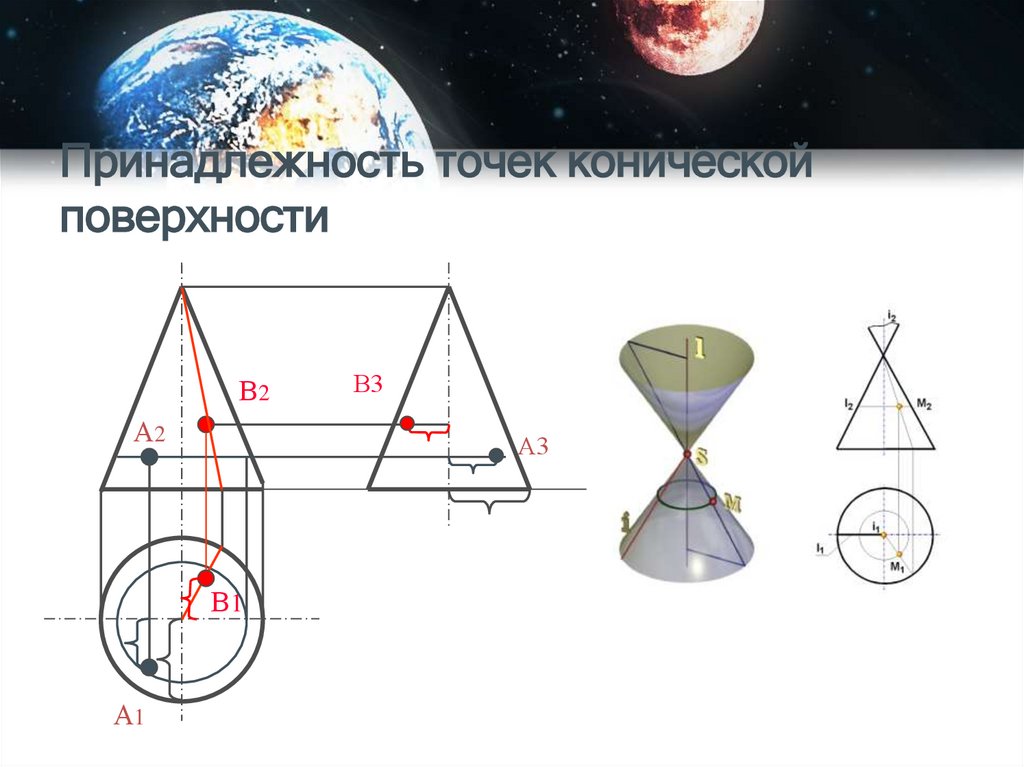
30. Принадлежность точек конической поверхности

В2
А2
А3
В1
А1
В3

31.

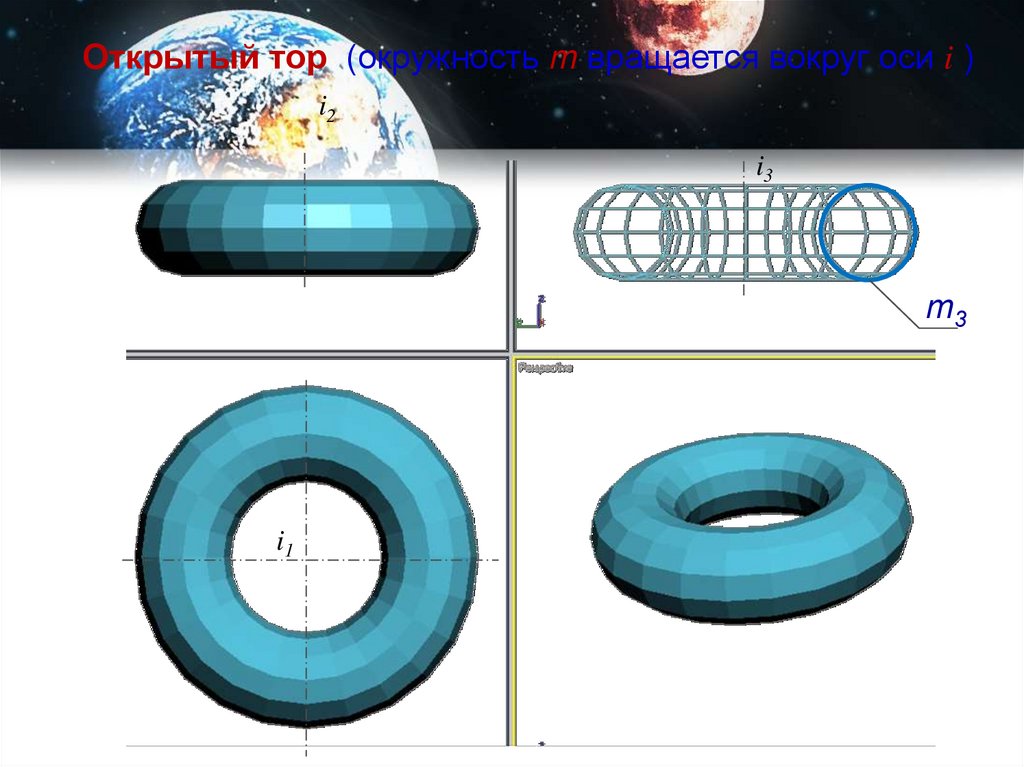
Открытый тор (окружность m вращается вокруг оси i )
i2
i3
m3
i1

32.

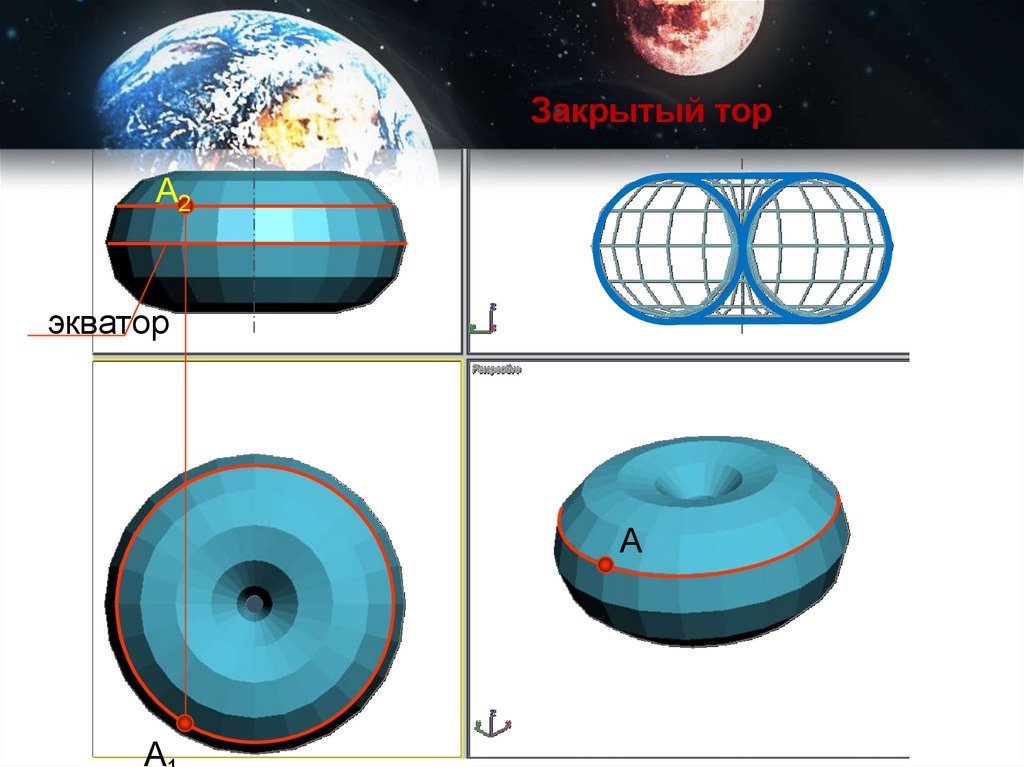
Закрытый тор
А2
экватор
А
А

33.

Многогранные поверхности – это
поверхности, образованные частями
(отсеками) пересекающихся плоскостей
Многогранником называется тело,
ограниченное многогранной поверхностью,
состоящей из плоских многоугольников
Отсеки плоскостей называются гранями,
а линии их пересечения – ребрами
Точки пересечения ребер называются
вершинами

34.

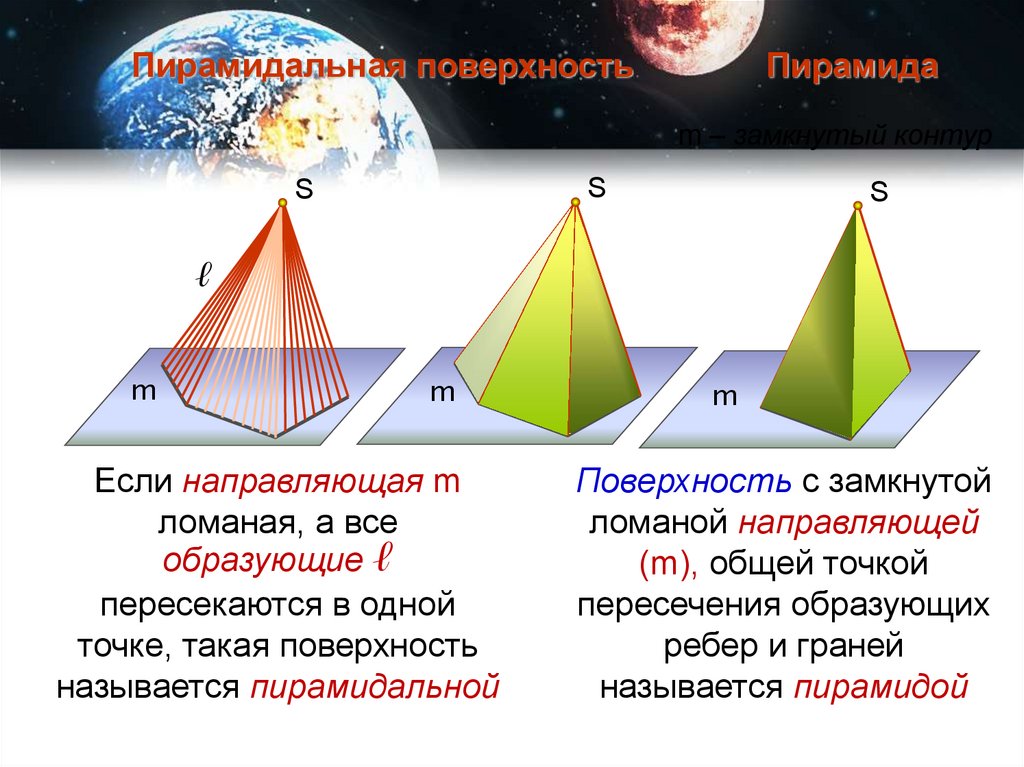
Пирамидальная поверхность
Пирамида
m – замкнутый контур
S
S
S
ℓ
m
m
Если направляющая m
ломаная, а все
образующие ℓ
пересекаются в одной
точке, такая поверхность
называется пирамидальной
m
Поверхность с замкнутой
ломаной направляющей
(m), общей точкой
пересечения образующих
ребер и граней
называется пирамидой

35.

Призма
Призматическая поверхность
S
ℓ
m
Если все образующие
поверхности
параллельны –
поверхность
называется
призматической
S
ℓ
m
Поверхность с замкнутой
ломаной направляющей
(m) (основанием) и
взаимно параллельными
ребрами – призма

36.

Проецирующая призма
k
С
А
f2
g
2
2
В
А1
С
В1
1
X1,
2
g
k
1
1
f1
Если ребра призмы перпендикулярны основанию,
гранник называется проецирующей призмой

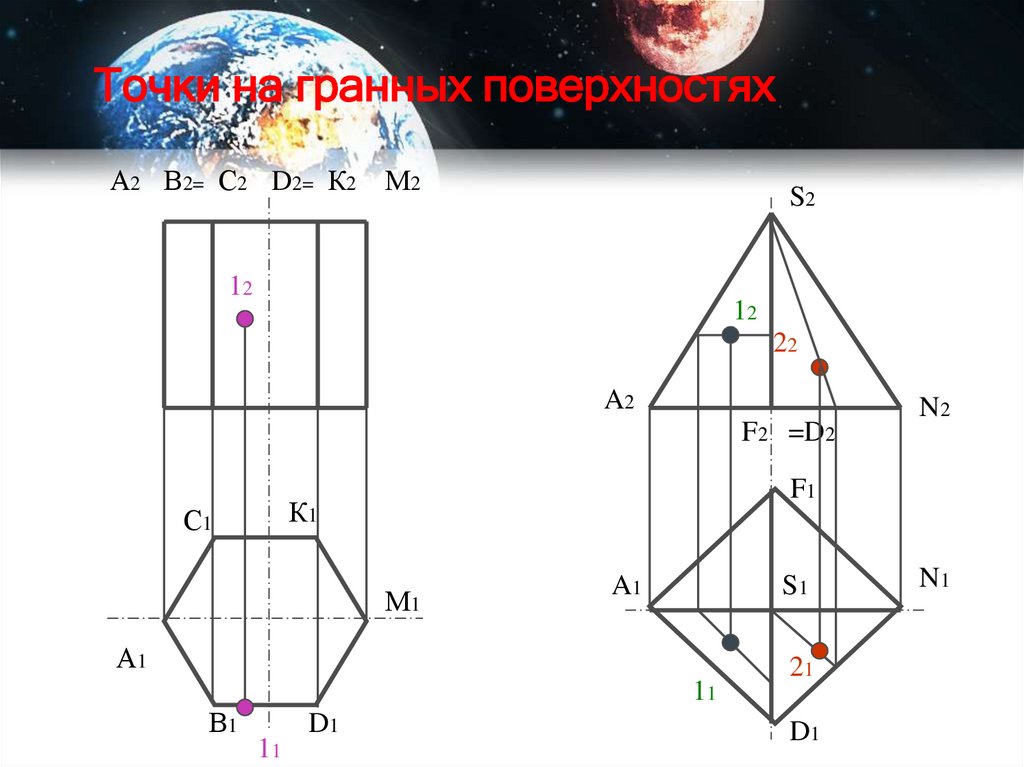
37. Точки на гранных поверхностях

А2 В2= С2 D2= К2 М2
S2
12
12
22
A2
F2 =D2
F1
К1
С1
М1
A1
S1
А1
11
В1
11
D1
N2
21
D1
N1