Метричесие задачи поверхности. (Лекция 3)

1. (ГТУ) Московский Институт Стали и Сплавов

Лекция №3
МЕТРИЧЕСИЕ ЗАДАЧИ
ПОВЕРХНОСТИ
Материал создан на базе кура лекций
по
Начертательной геометрии,
разработанного доцентом кафедры
Инженерной графики МИСиС
Мокрецовой Л.О.- [email protected]
Автор:
Головкина Валерия Борисовна
[email protected]
2008

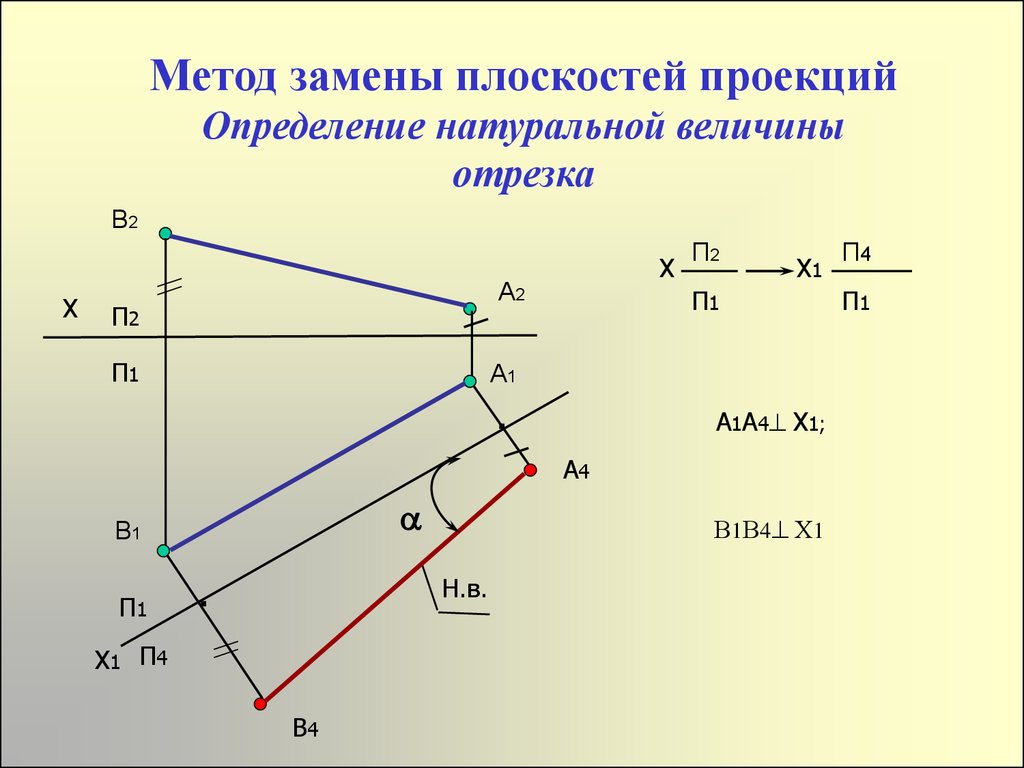
2. Метод замены плоскостей проекций Определение натуральной величины отрезка

В2
Х
Х
А2
П2
П1
П2
Х1
П1
А1
А1А4 Х1;
▪
А4
В1
П1
В1В4 Х1
Н.в.
▪
Х1 П4
В4
П4
П1

3. Метод прямоугольного треугольника

A2
Задано: Две проекции отрезка АВ ;
Н.В.
Построить:
В0
X
AX
2
B2 ΔY=YВYА
BX
1
A1
ΔY=YвB1YА
Действительный вид АВ.
Решение:
1.Возьмем разность координат Y
точек А и В;
2. Восставим перпендикуляр из
любой точки отрезка к А2В2;
3.Отложим вверх от т.В2
отрезок равный ΔY|А-В| ;
4. Соединяем А2 и В0 .

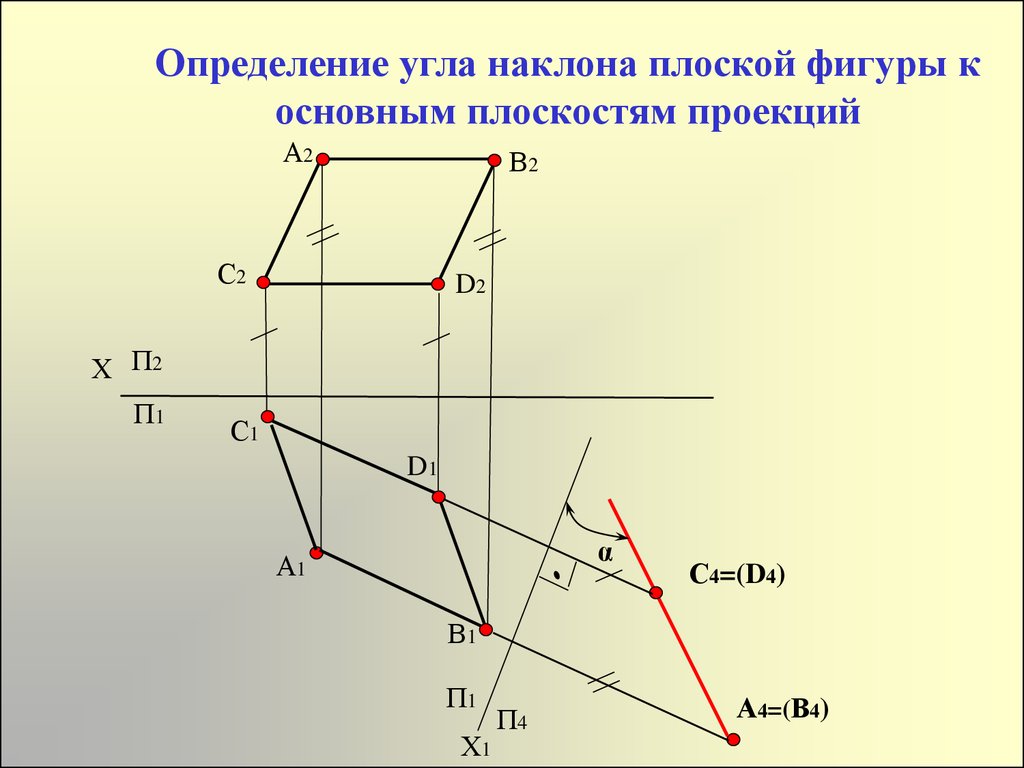
4. Определение угла наклона плоской фигуры к основным плоскостям проекций

А2
В2
С2
D2
Х П2
П1
С1
D1
α
А1
С4=(D4)
В1
П1
Х1
П4
А4=(В4)

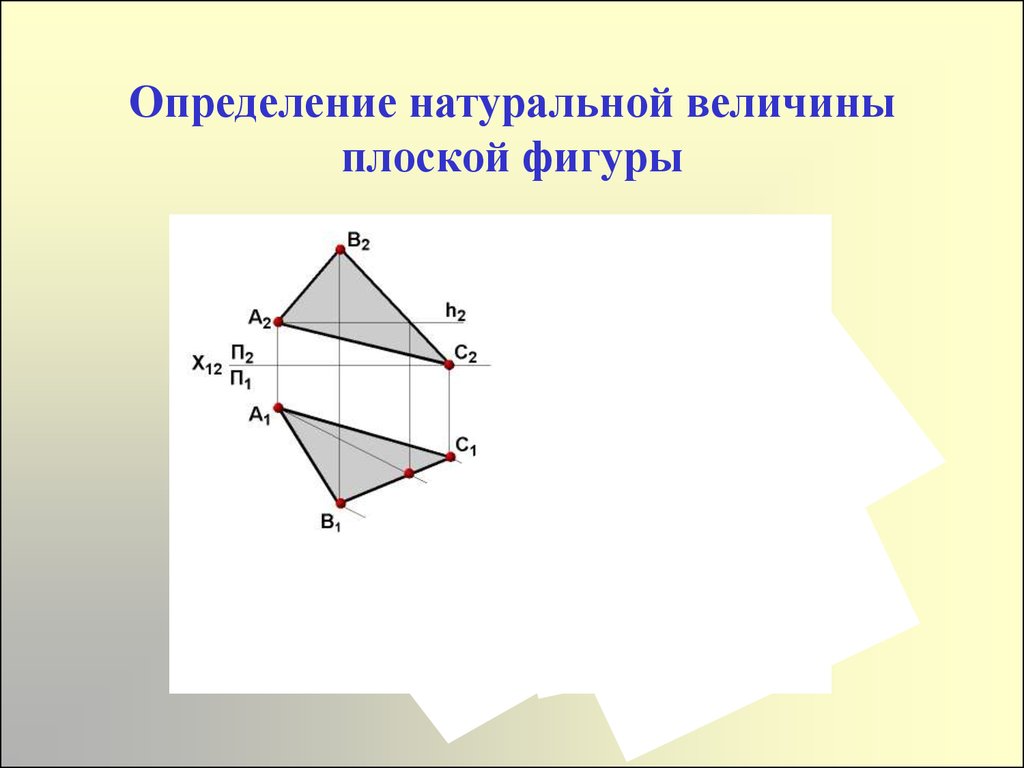
5. Определение натуральной величины плоской фигуры

С4
А4
В4

6.

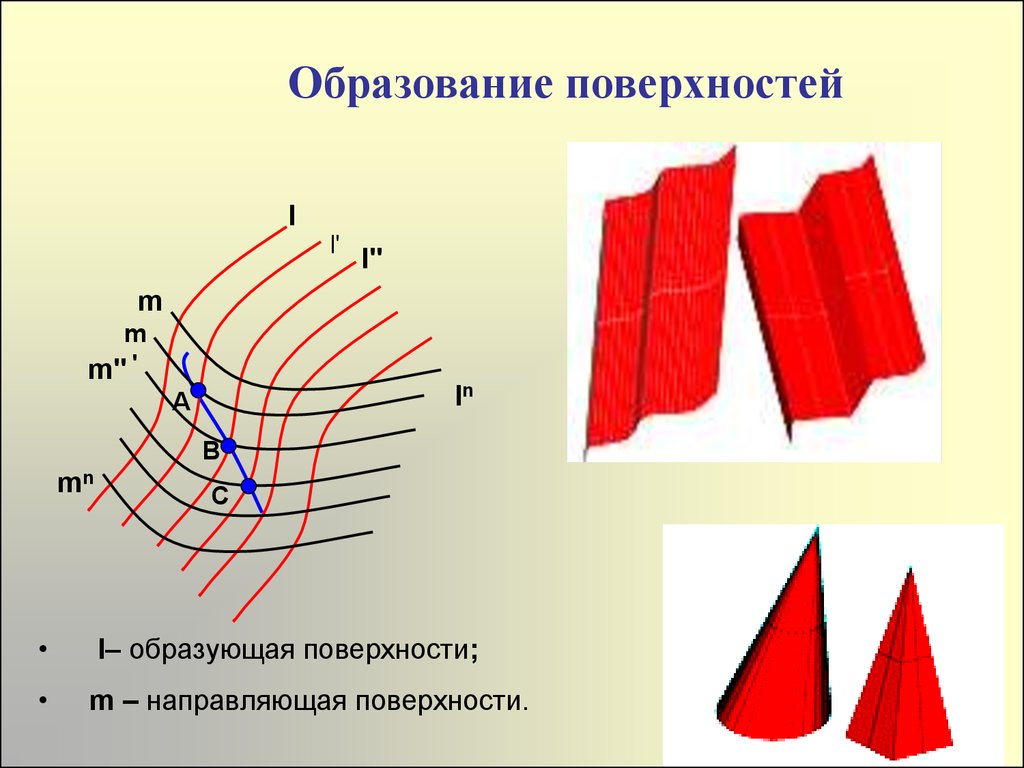
Образование поверхностей
l
l'
l"
m
m
m" '
ln
A
B
mn
C
l– образующая поверхности;
m – направляющая поверхности.

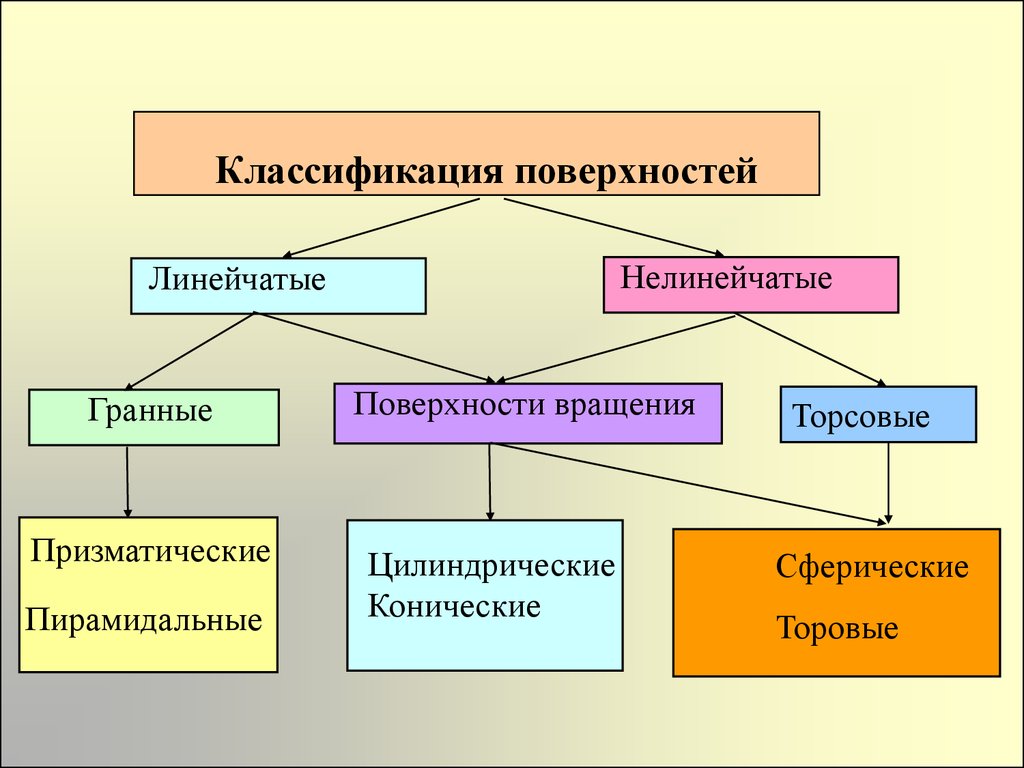
7. Классификация поверхностей

Нелинейчатые
Линейчатые
Гранные
Призматические
Пирамидальные
Поверхности вращения
Цилиндрические
Конические
Торсовые
Сферические
Торовые

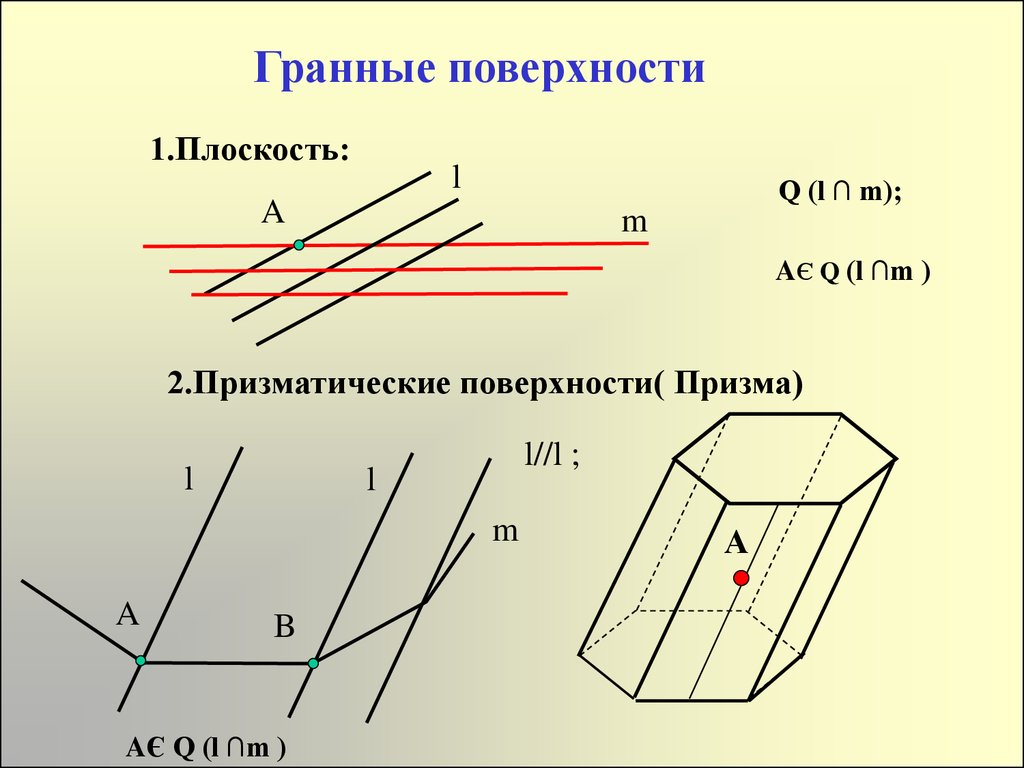
8. Гранные поверхности

1.Плоскость:
l
Q (l ∩ m);
A
m
AЄ Q (l ∩m )
2.Призматические поверхности( Призма)
l
l//l ;
l
m
A
B
AЄ Q (l ∩m )
А

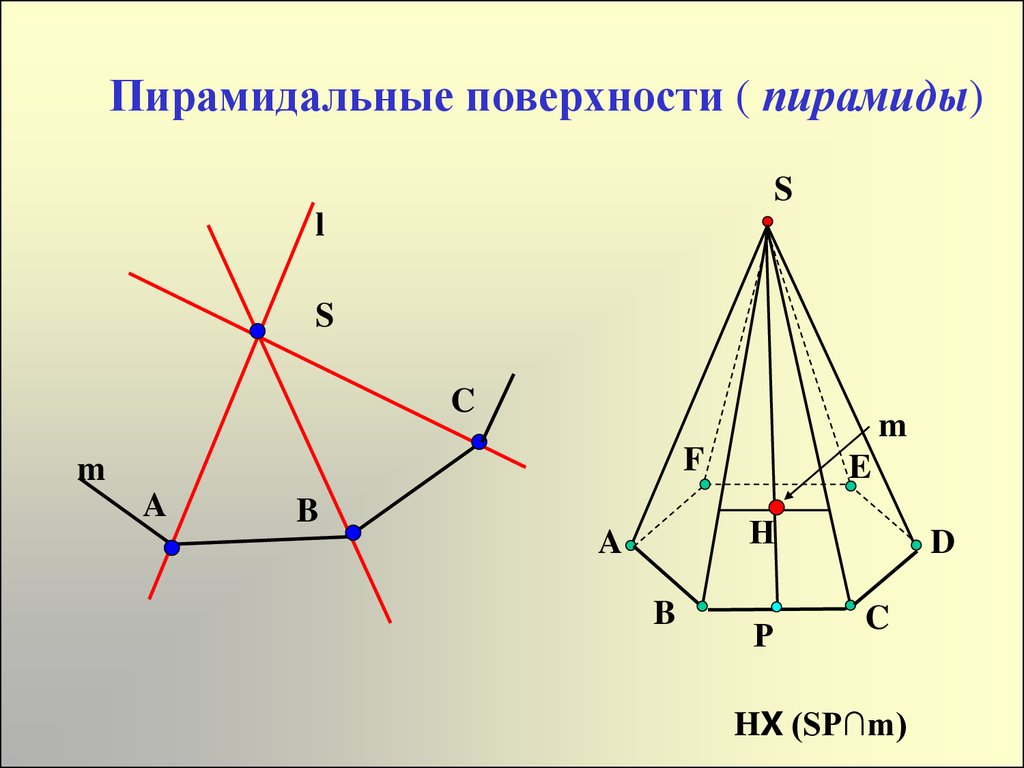
9.

Пирамидальные поверхности ( пирамиды)
S
l
S
C
m
F
m
A
B
E
Н
A
B
Р
D
C
HX (SP∩m)

10. Точки на гранных поверхностях

А2 В2= (С2) D2= (К2) М2
S2
12
12
22
A2
(F2) =D2
С1
F1
К1
М1
A1
S1
А1
11
В1
(11)
D1
N2
21
D1
N1

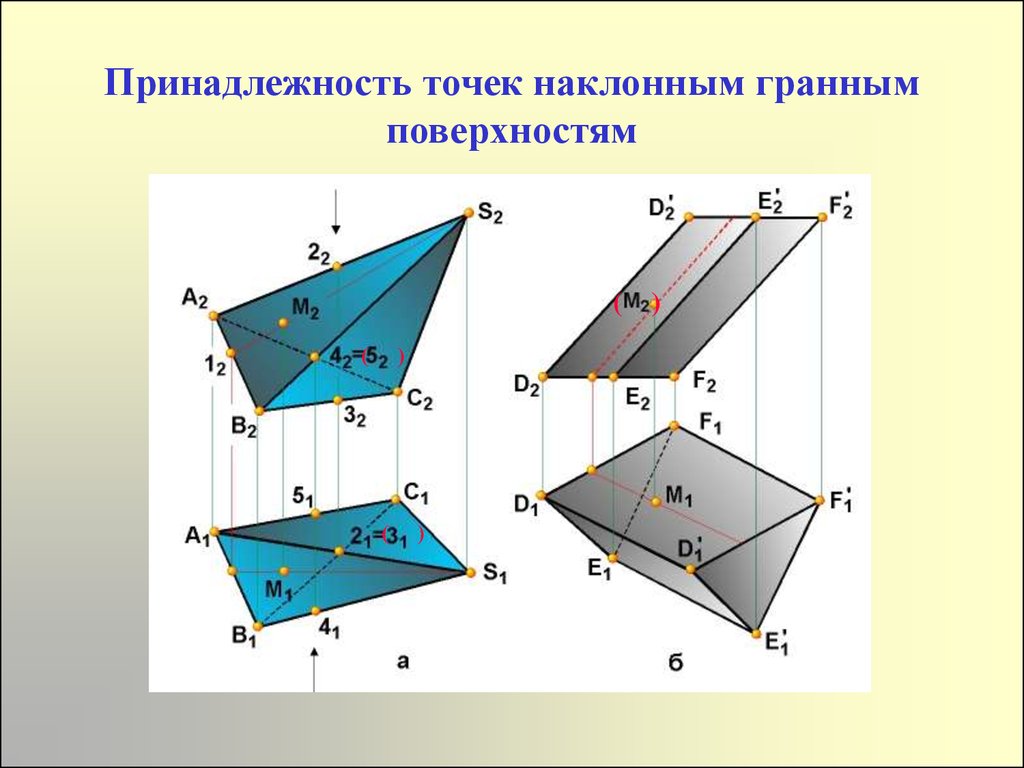
11. Принадлежность точек наклонным гранным поверхностям

( )
(
)
(
)

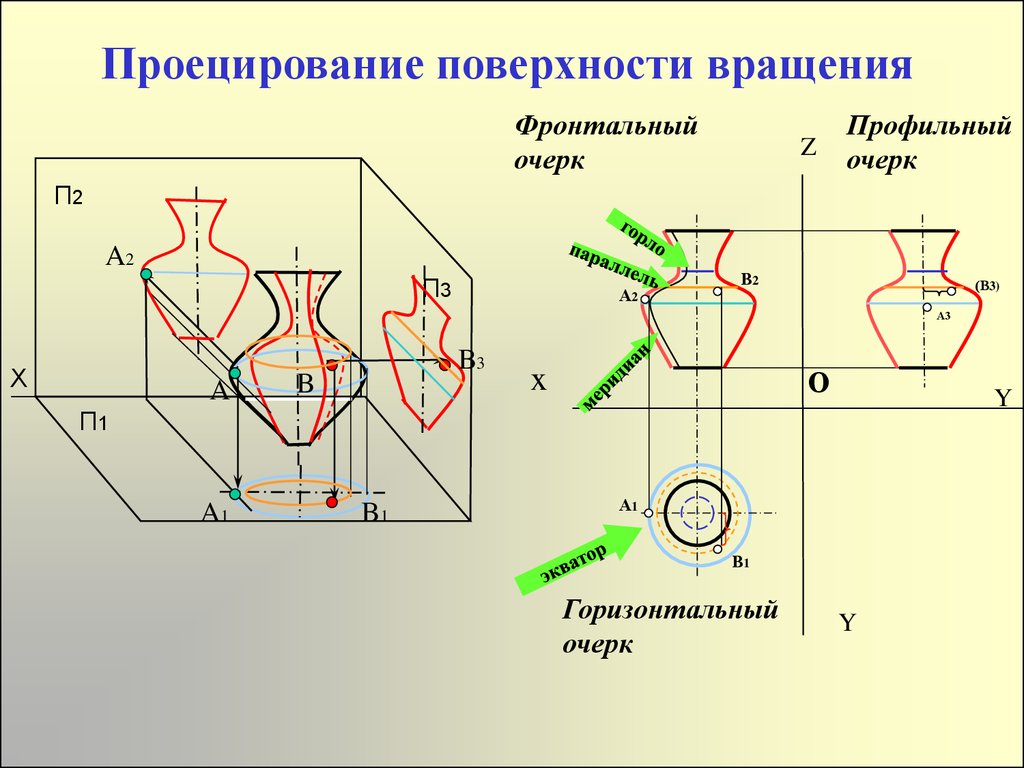
12. Проецирование поверхности вращения

Фронтальный
очерк
Z
Профильный
очерк
П2
A2
П3
А2
В2
(В3)
А3
Х
A
B3
B
x
О
Y
П1
A1
B1
А1
В1
Горизонтальный
очерк
Y

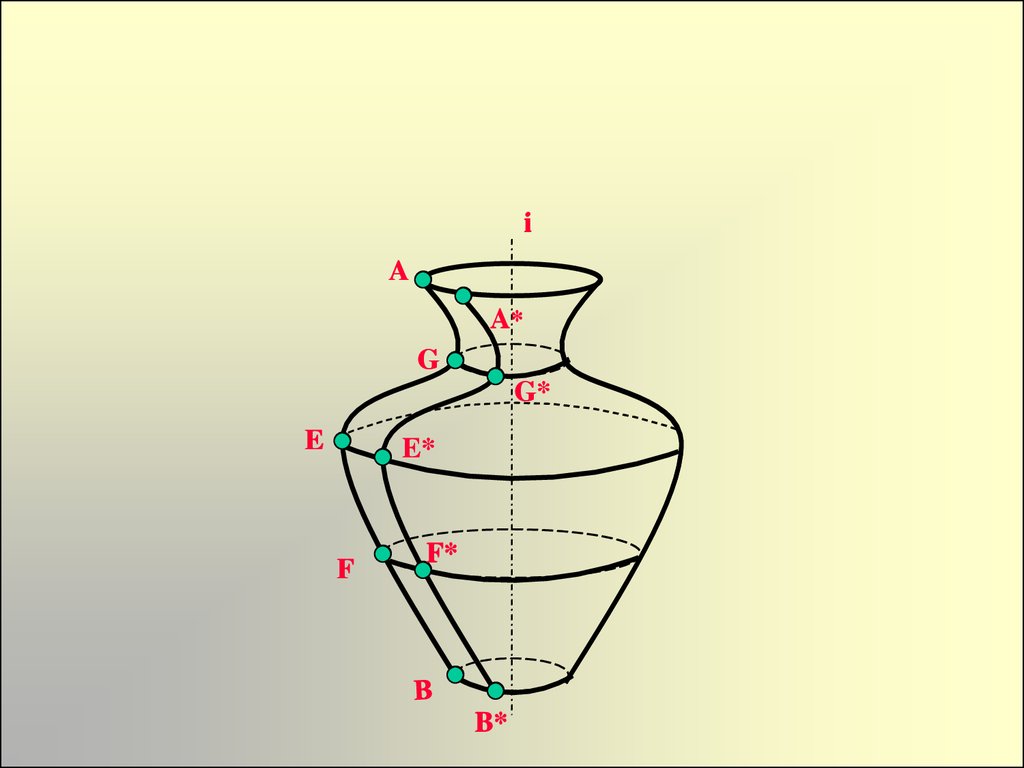
13.

i
A
A*
G
G*
E
E*
F
F*
B*

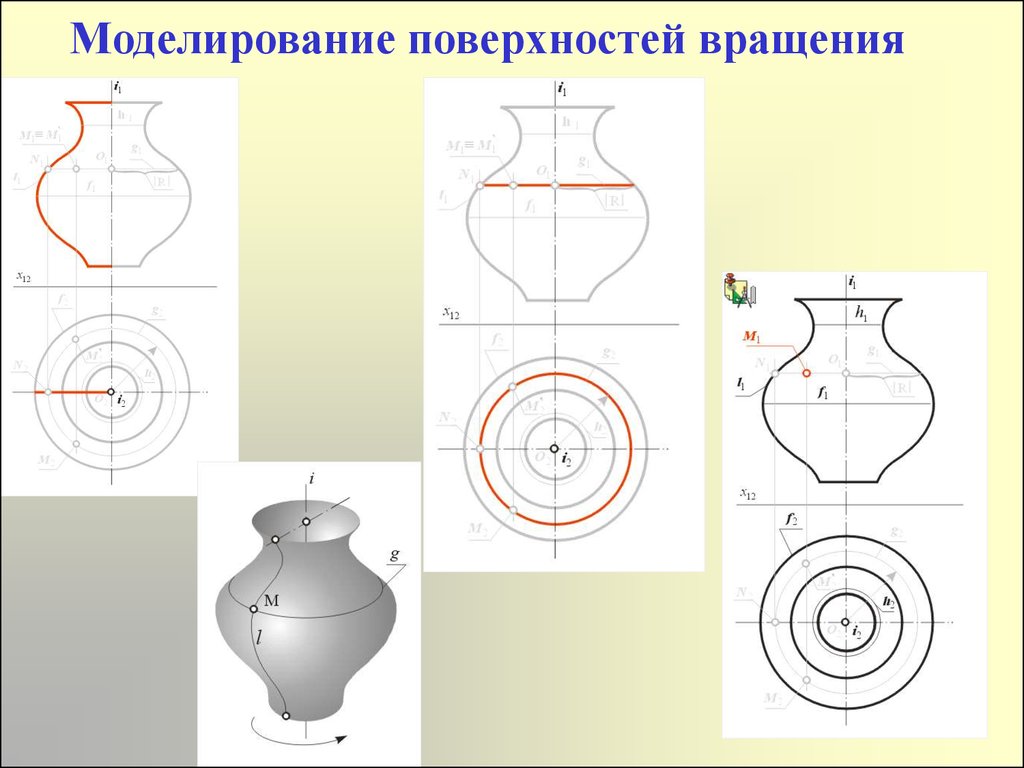
14. Моделирование поверхностей вращения

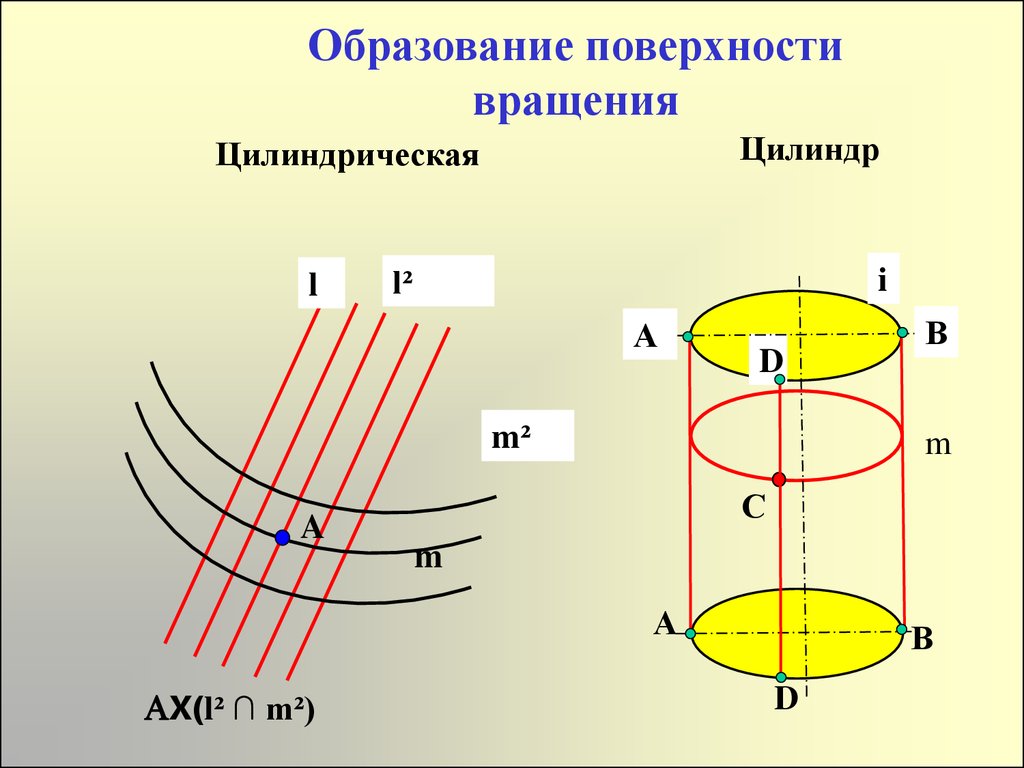
15. Образование поверхности вращения

Цилиндр
Цилиндрическая
l
l²
i
А
D
m²
A
m
С
m
А
AX(l² ∩ m²)
В
В
D

16. Принадлежность точки поверхности цилиндра

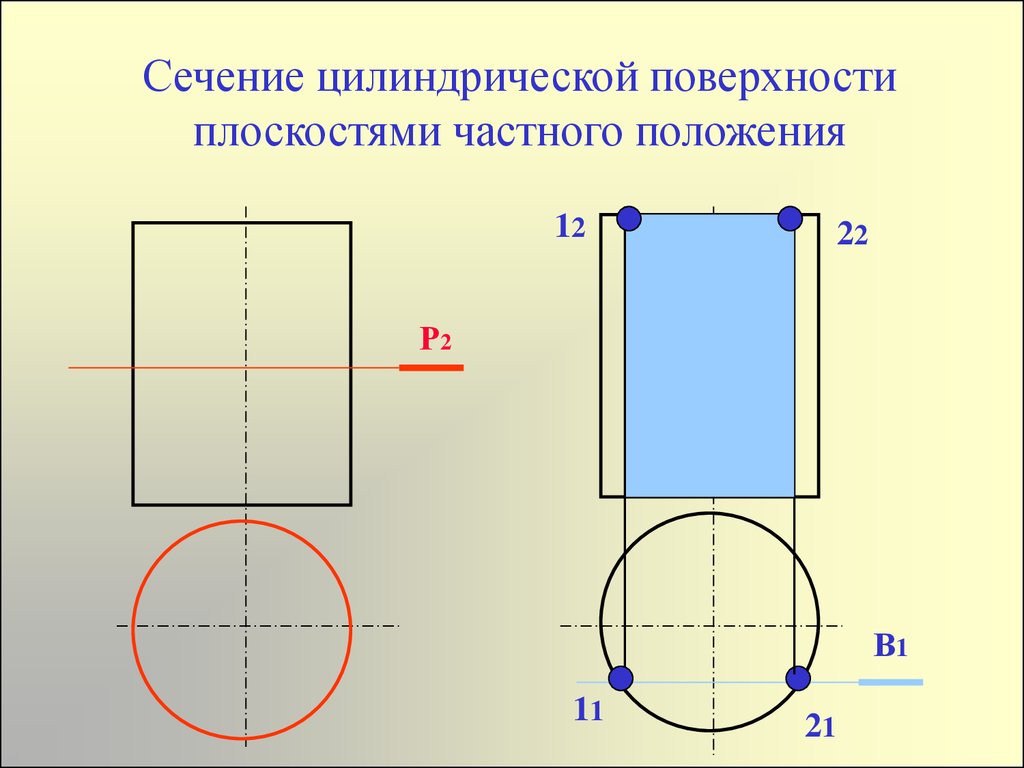
17. Сечение цилиндрической поверхности плоскостями частного положения

12
22
Р2
В1
11
21

18.

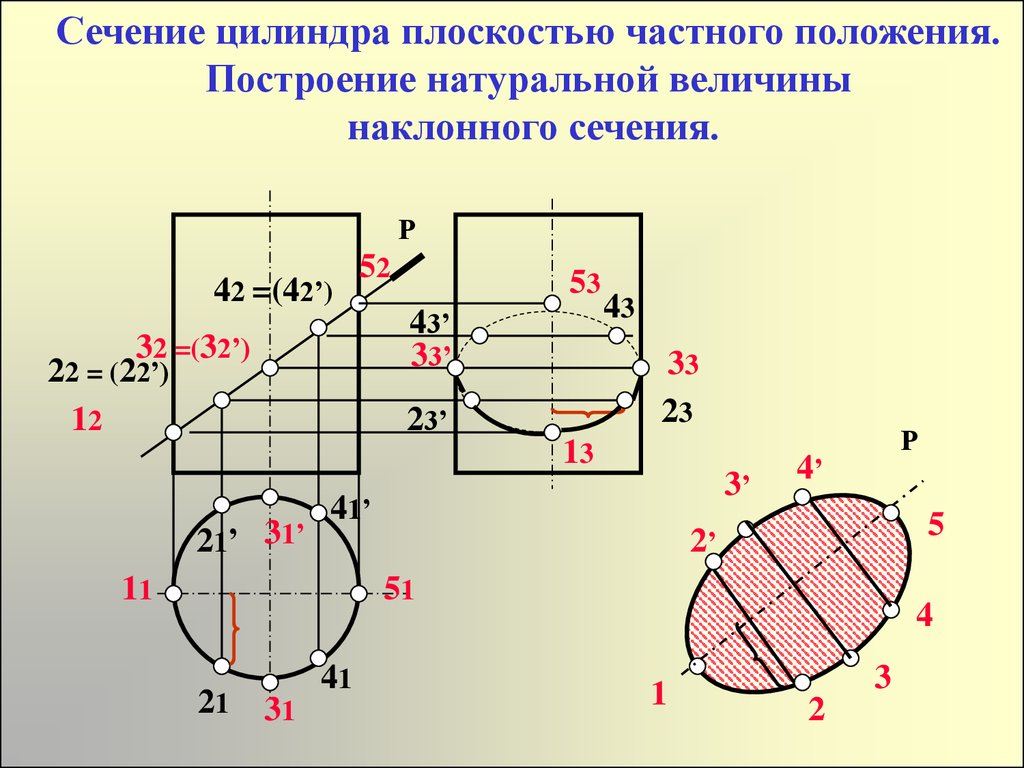
Сечение цилиндра плоскостью частного положения.
Построение натуральной величины
наклонного сечения.
Р
42 =(42’)
52
32 =(32’)
22 = (22’)
12
53
43’
33’
43
33
23
23’
13
21’ 31’
3’
41’
11
Р
4’
5
2’
51
21
41
31
4
1
3
2

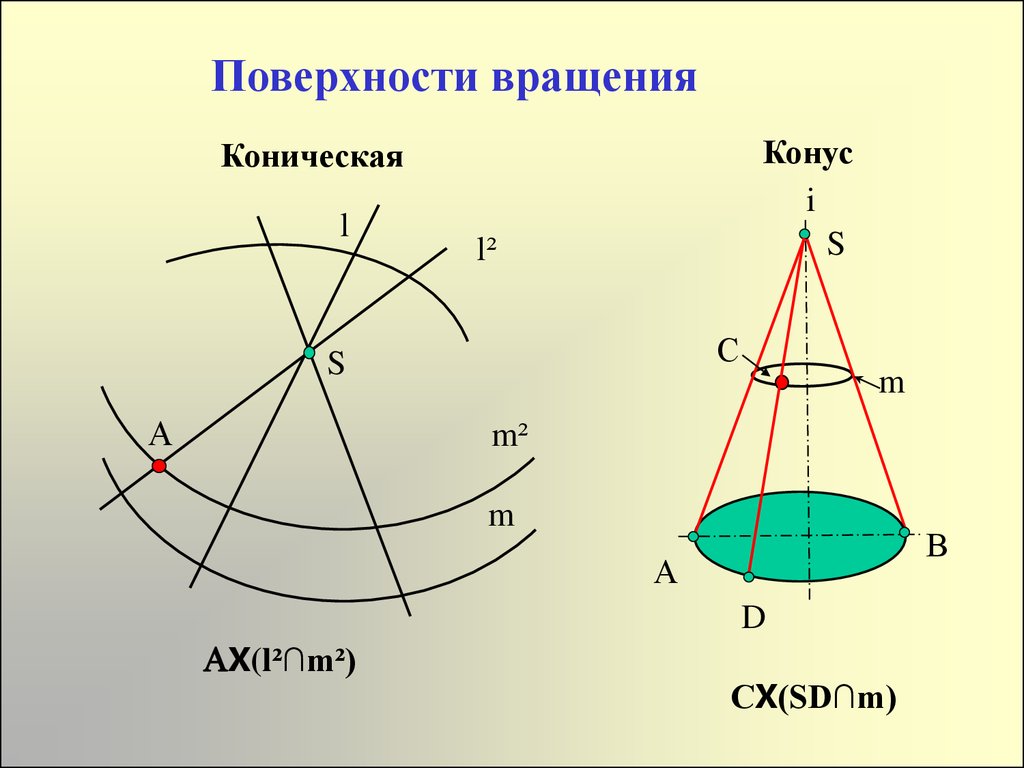
19. Поверхности вращения

Конус
i
S
Коническая
l
l²
С
S
A
m
m²
m
В
А
D
AX(l²∩m²)
СX(SD∩m)

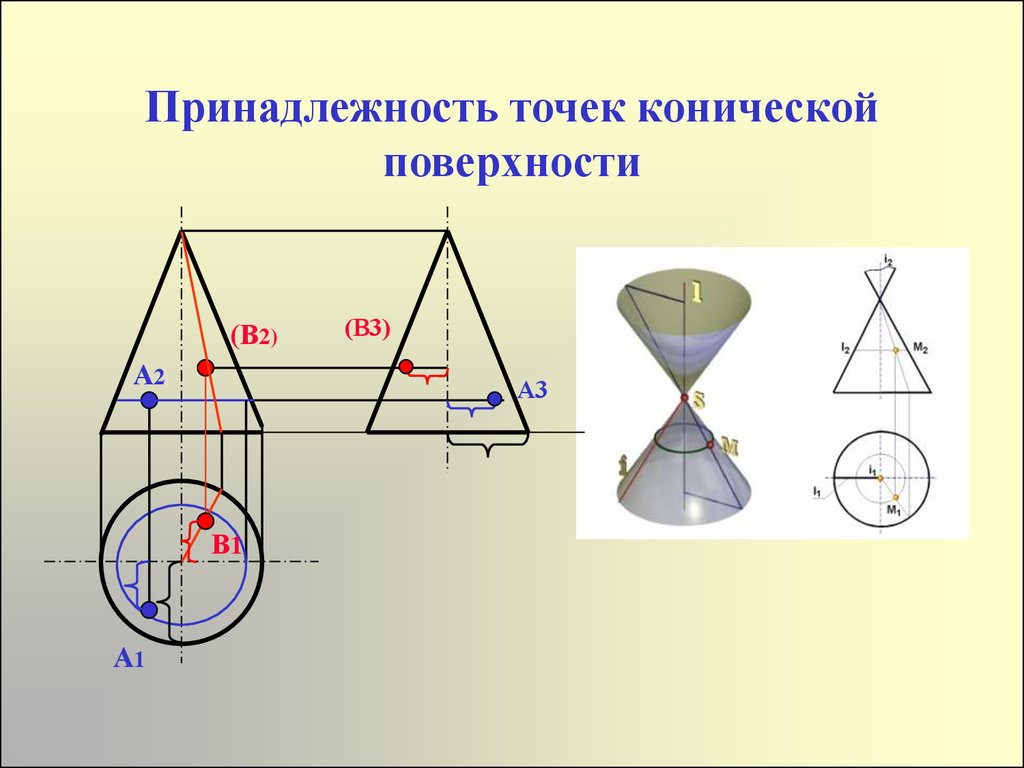
20. Принадлежность точек конической поверхности

(В2)
А2
А3
В1
А1
(В3)

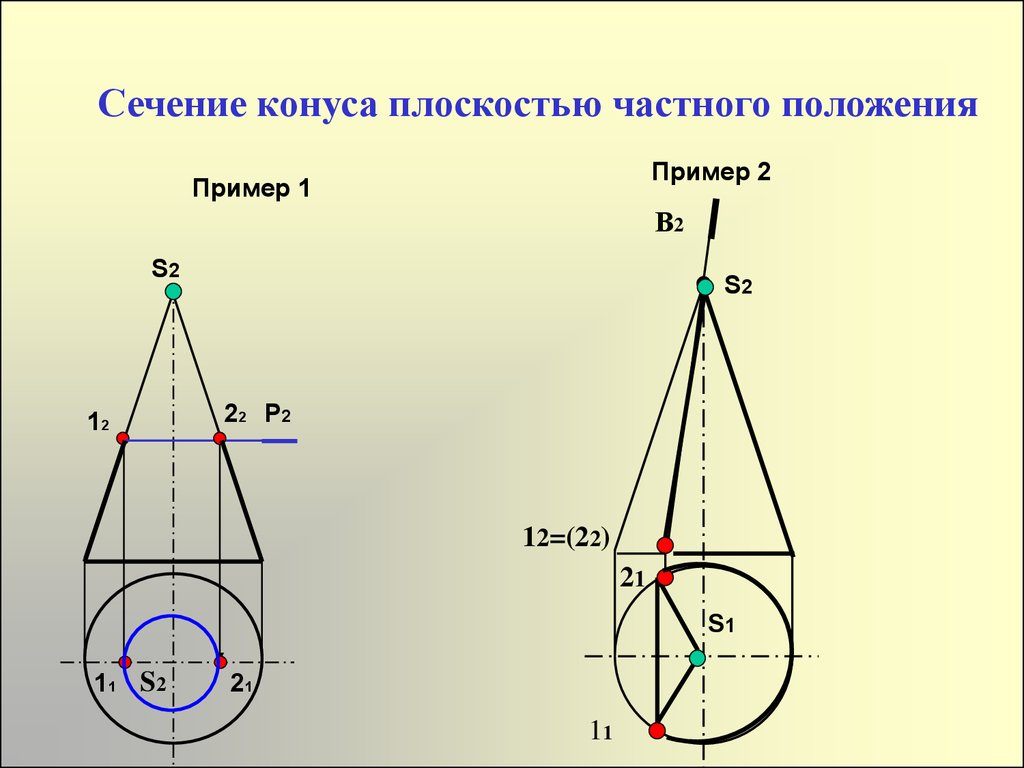
21. Сечение конуса плоскостью частного положения

Пример 2
Пример 1
В2
S2
12
S2
22 Р2
12=(22)
21
S1
11 S2
21
11

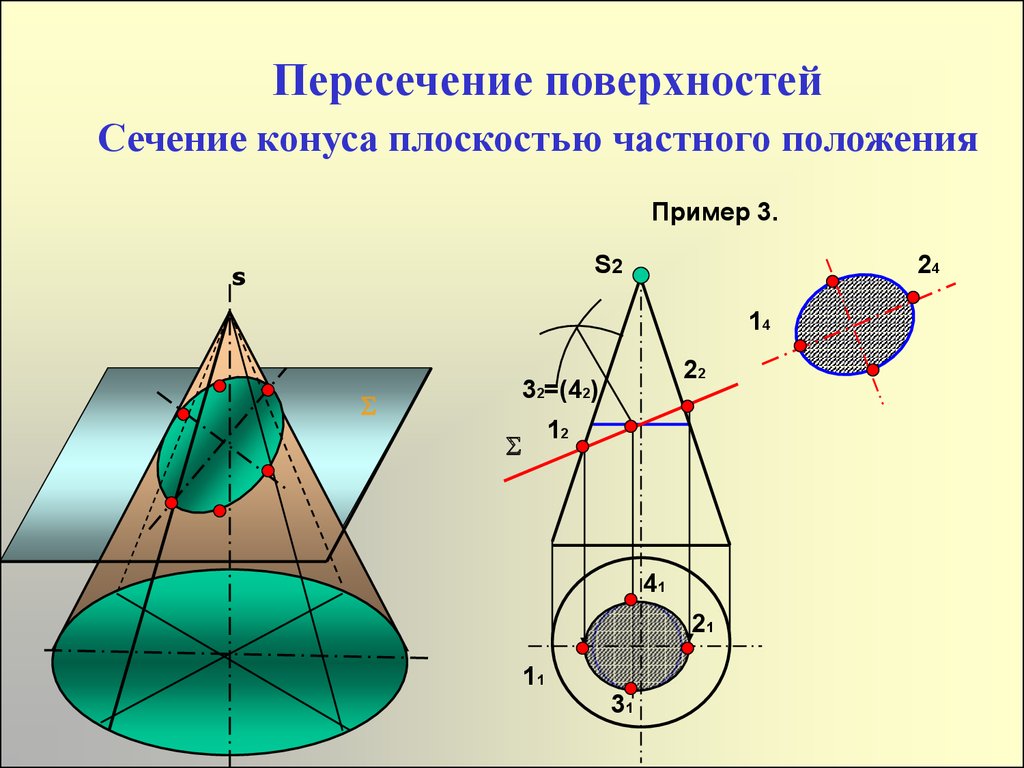
22. Пересечение поверхностей Сечение конуса плоскостью частного положения

Пример 3.
S2
s
24
14
22
32=(42)
12
41
21
11
31

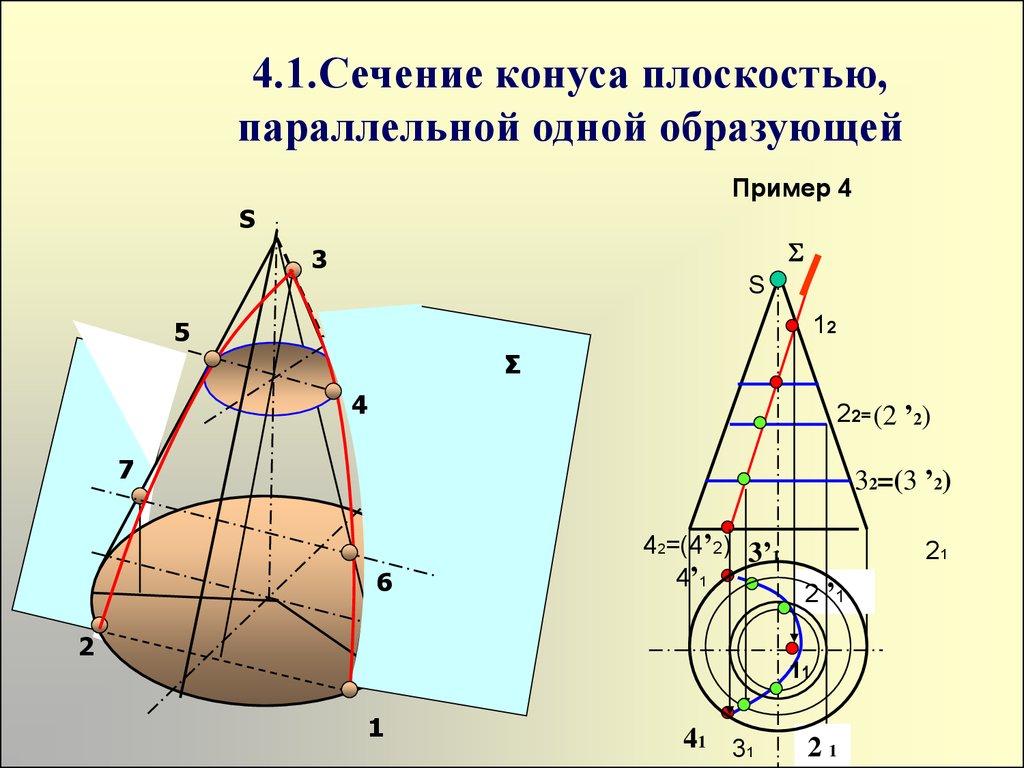
23. 4.1.Сечение конуса плоскостью, параллельной одной образующей

Пример 4
S
3
S
12
5
Σ
4
Σ
22= (2 ’2)
7
32=(3 ’2)
6
42=(4’2) 3’1
4’1
21
2 ’1
2
11
1
41 31
21

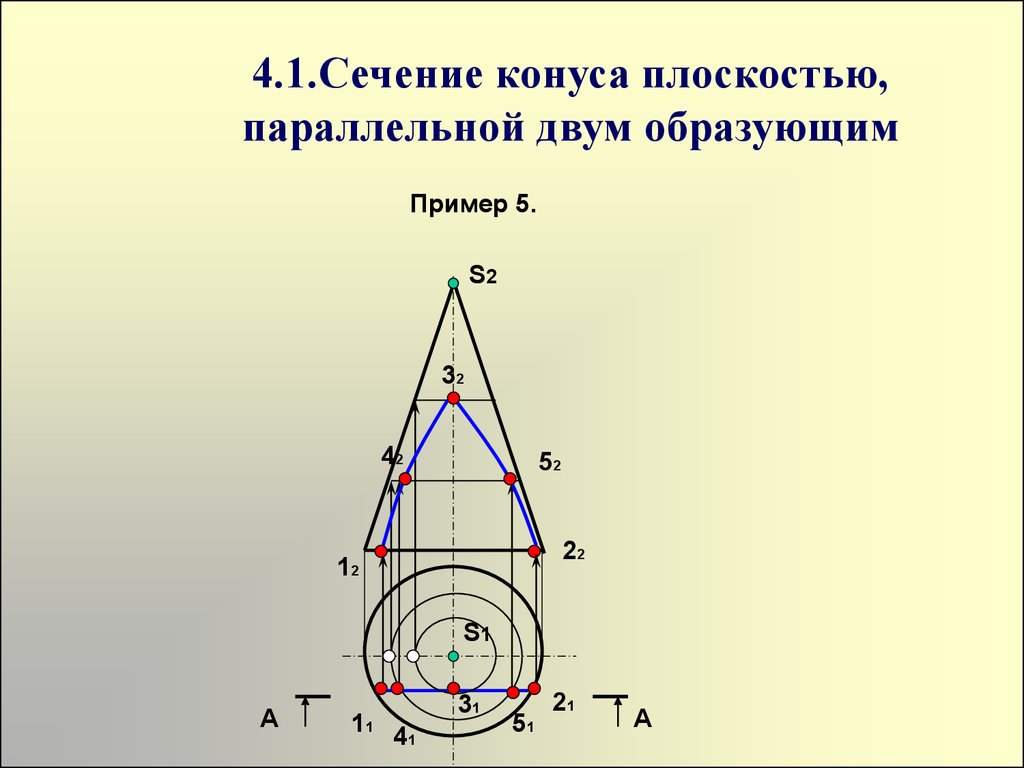
24. 4.1.Сечение конуса плоскостью, параллельной двум образующим

Пример 5.
S2
32
42
52
22
12
S1
А
11
31
41
51
21
А

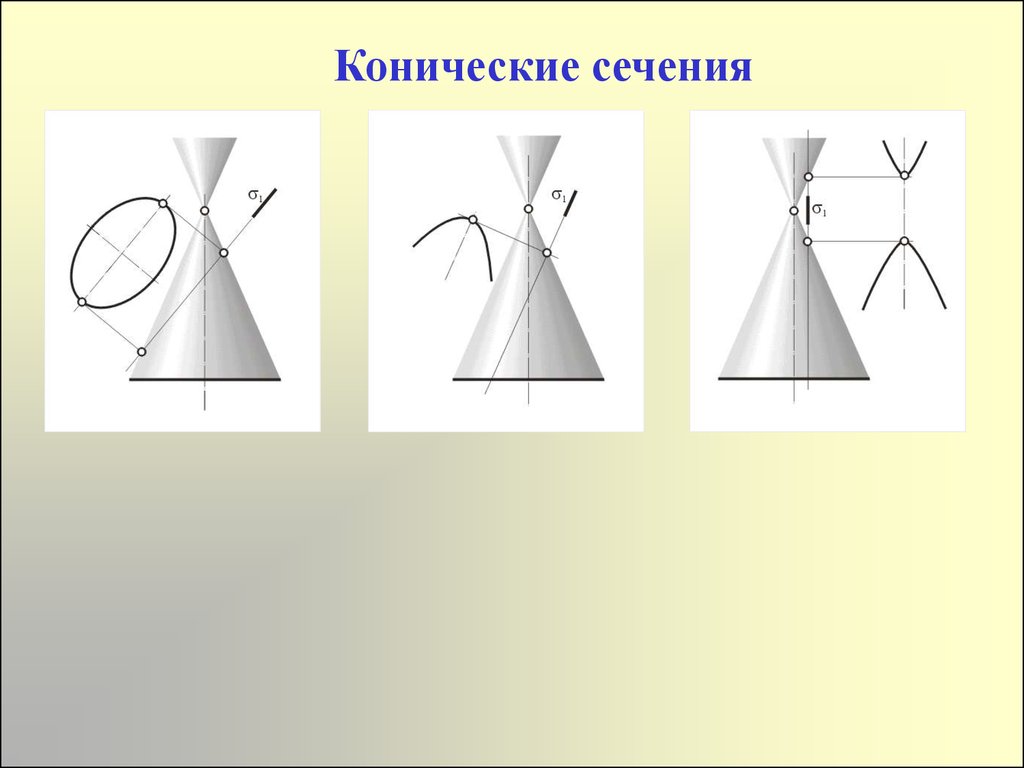
25. Конические сечения

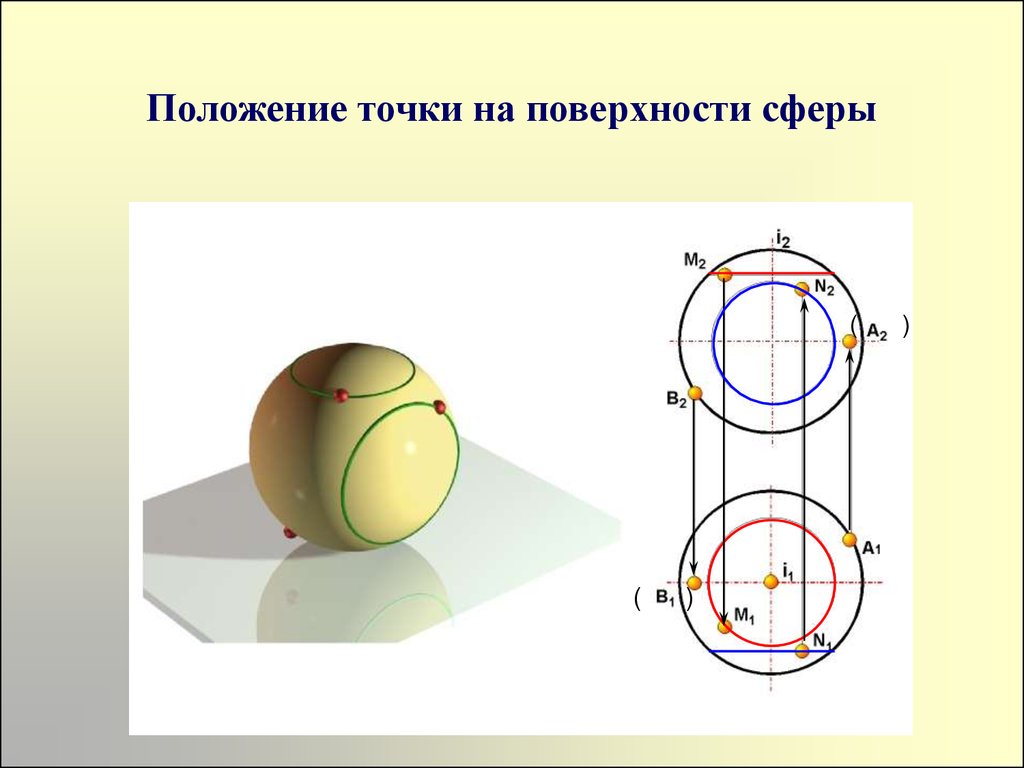
26. Положение точки на поверхности сферы

(
(
)
)

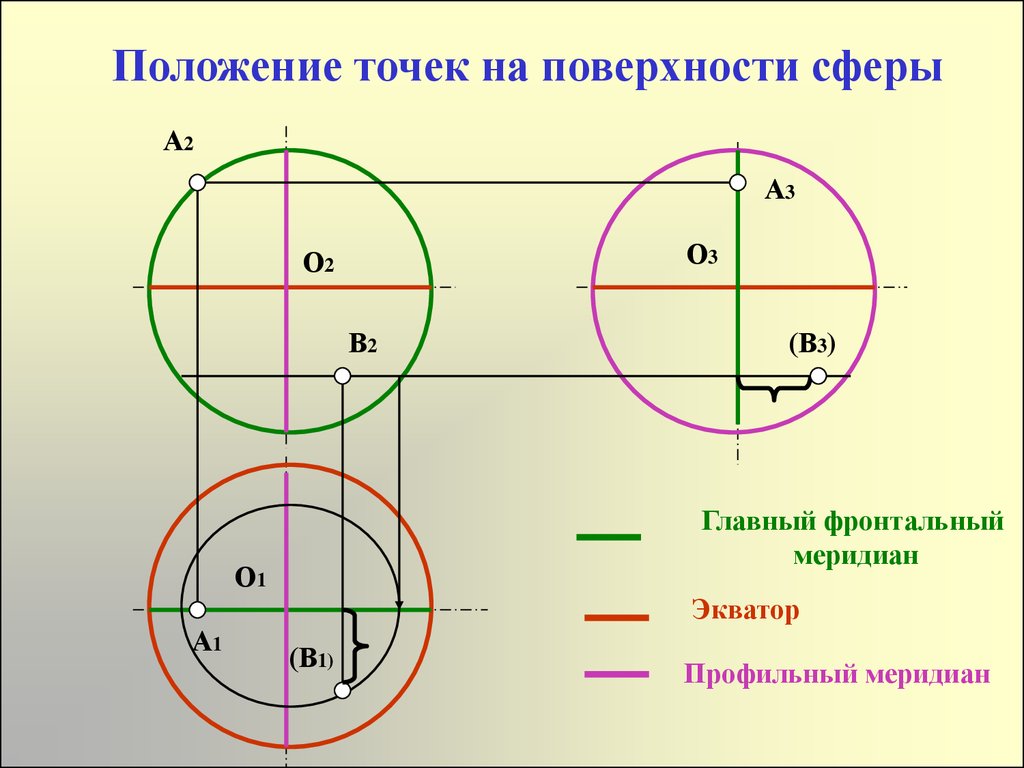
27. Положение точек на поверхности сферы

А2
А3
О3
О2
В2
(В3)
Главный фронтальный
меридиан
О1
Экватор
А1
(В1)
Профильный меридиан

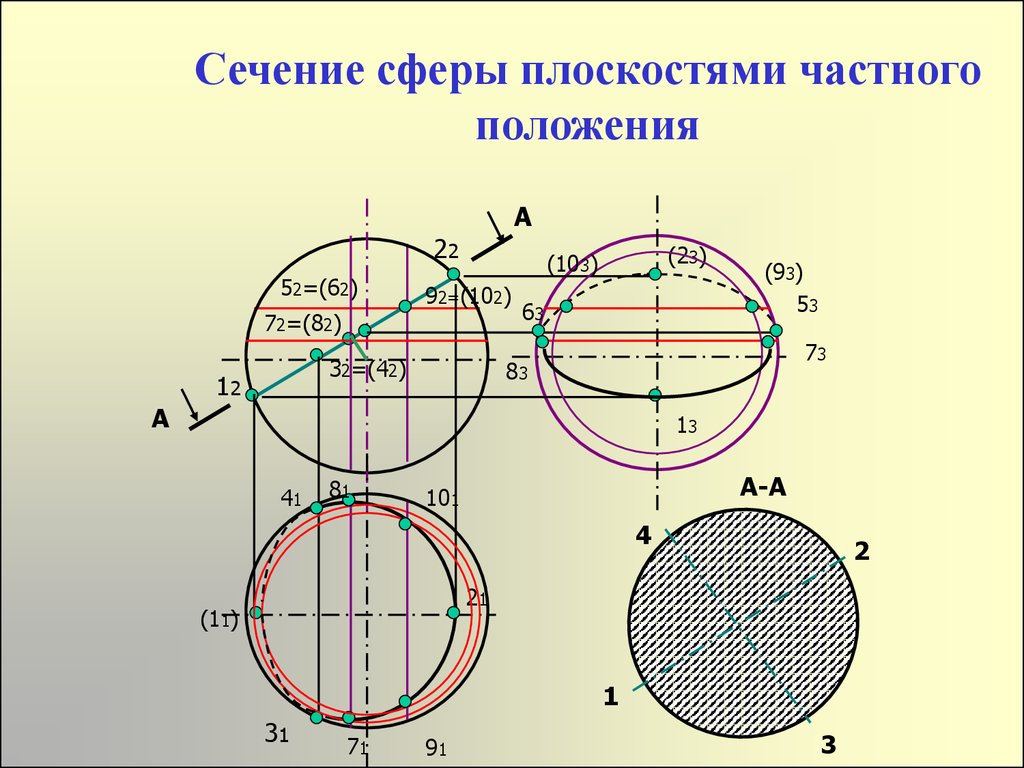
28. Сечение сферы плоскостями частного положения

А
22
52=(62)
72=(82)
92=(102)
32=(42)
12
(23)
(103)
63
(93)
53
73
83
А
13
41
81
А-А
101
4
2
21
(11)
1
31
71
91
3

29.

Поверхности вращения
в) Сфера ( шар)
а) Открытый тор
( тор-кольцо):
б)Закрытый тор:
А
В
С

30.

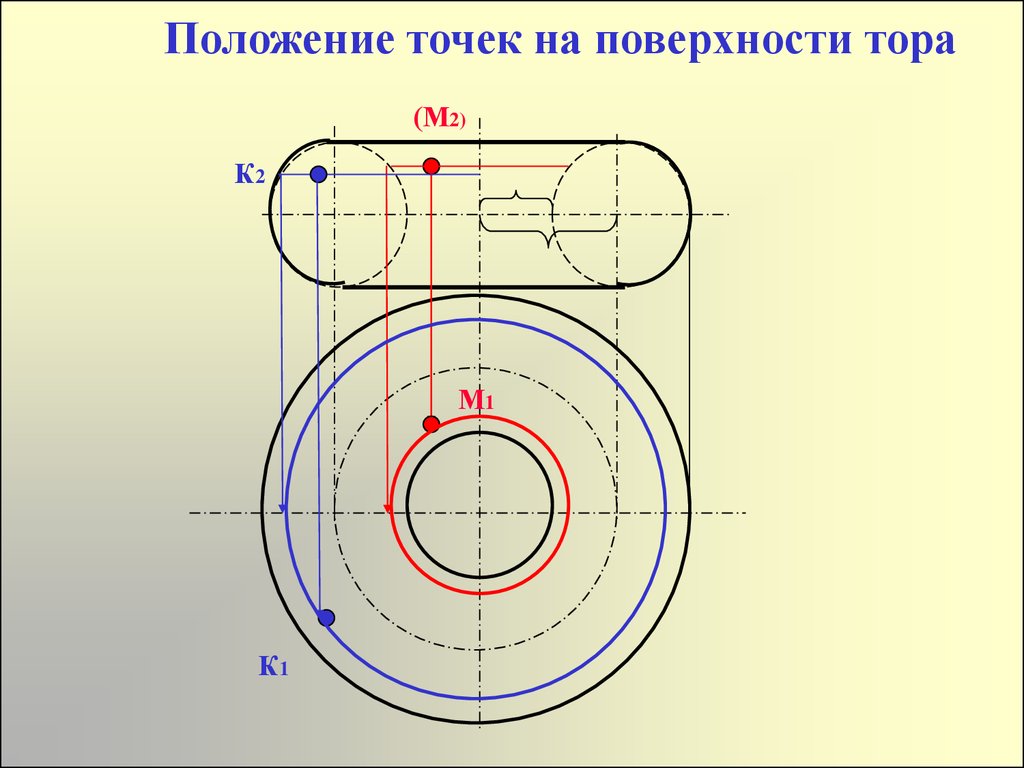
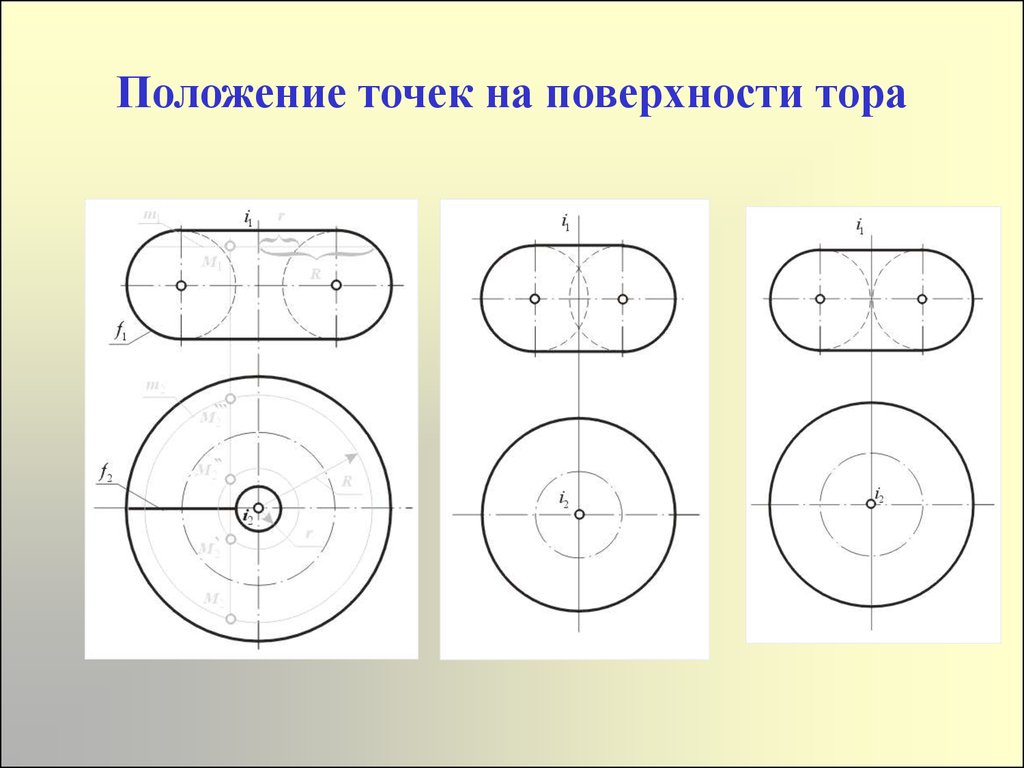
Положение точек на поверхности тора

31. Положение точек на поверхности тора

(М2)
К2
М1
К1

32.

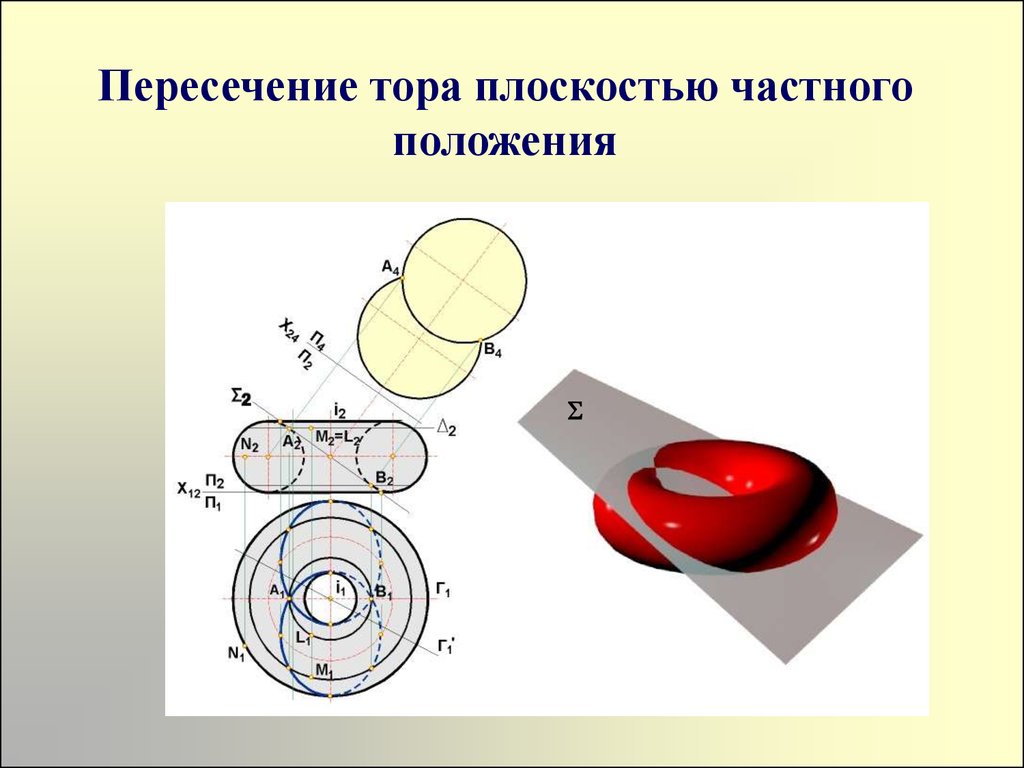
Положение точек на поверхности тора

33. Пересечение тора плоскостью частного положения

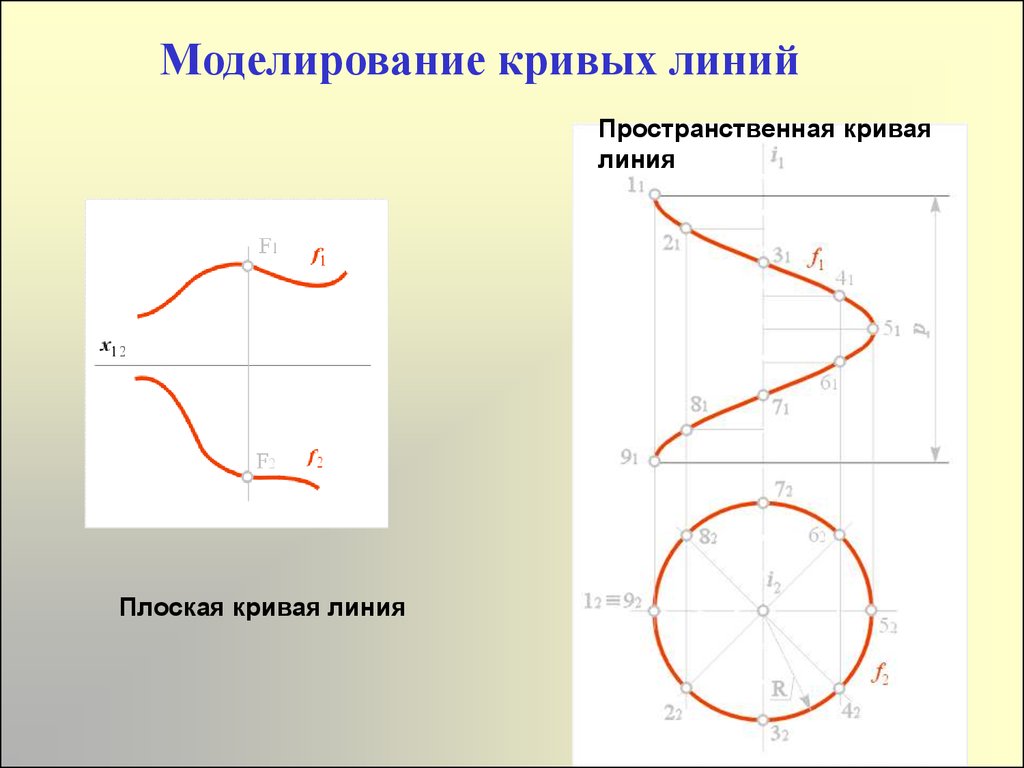
34. Моделирование кривых линий

Пространственная кривая
линия
Плоская кривая линия

35.

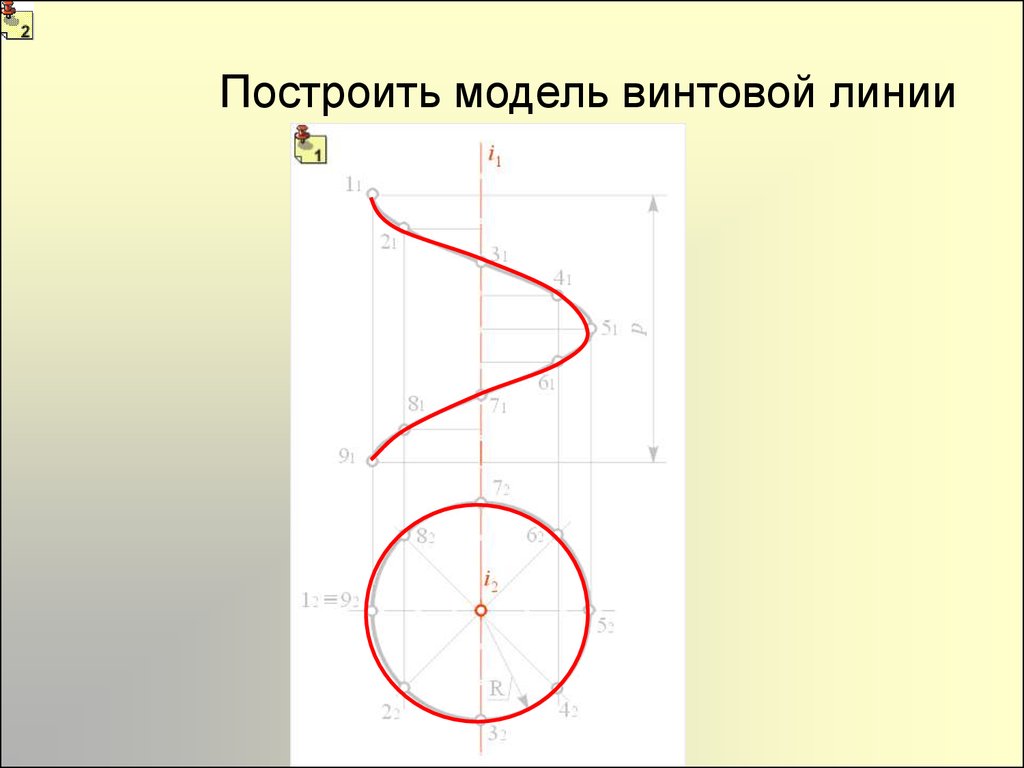
Построить модель винтовой линии

36.

Построить недостающую
проекцию точки М,
принадлежащей
поверхности
однополостного
гиперболлоида
Построить недостающие
проекцию точек М и N,
принадлежащих поверхности
двуполостного
гиперболлоида.

37. Параболоид вращения.

38. Линейчатые поверхности с плоскостью параллелизма

• ·
Цилиндроид – прямолинейная
образующая движется по первой и
второй направляющим, являющимися
кривыми линиями, параллельно
заданной плоскости.
• ·
·
Косая плоскость
(гиперболический параболоид) –
прямолинейная образующая движется
по первой и второй направляющим,
являющимися прямыми линиями,
параллельно заданной плоскости.

39.

• Коноид – прямолинейная
образующая движется по
первой и второй
направляющим, одна из
которых прямая линия, а
вторая – кривая линия,
параллельно заданной
плоскости.

40.

• Косая плоскость
(гиперболический
параболоид) –
прямолинейная
образующая движется по
первой и второй
направляющим,
являющимися прямыми
линиями, параллельно
заданной плоскости.

41. Каркасные поверхности

42. Построение точек пересечения проецирующей прямой с поверхностью

43. Построение линий пересечения проецирующей поверхности с поверхностью общего положения