Продольные колебания стержня. Семинар 13

1.

Семинар13. Продольные колебания стержня

2.

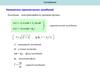
Основные типы краевых условий для продольных колебаний стержней
1.
u=0
дu
2. EF 0
дx
дu
3. EF N
дx
дu
4.1. EF cu 0
дx
дu
4.2. EF cu 0
дx
д 2u
дu
5.1. EF M 2
дt
дx
д 2u
дu
5.2. EF M 2
дt
дx

3.

1. Записать уравнение продольных колебаний стержня
д 2u д 2u
0 (8.2)
2
2
дx
E дt
д 2u 1 д 2u
2 2 0 (8.2а )
2
дx c0 дt
2. Записать решение уравнения продольных колебаний стержня
u ( x, t ) U ( x) sin t
( 8.3а )
3. Подставить решение в уравнение продольных колебаний стержня и
получить обыкновенное дифференциальное уравнение для функции U(x)
U U 0 (8.4) где
c0
2
(8.5)
4. Записать общее решение обыкновенного дифференциального
уравнения для функции U(x)
U ( x) C1 sin x C2 cos x
x=0 и
( 8.6)
5. Записать краевые условия для продольных колебаний стержня при
x=L относительно u(x,t)
6. Подставить решение (8.3a) в краевые условия относительно
u(x,t)

4.

7. Записать краевые условия при
x=0 и x=L относительно U(x)
8. Подставить общее решение (8.6) в краевые условия и получить
систему линейных однородных уравнений для определения С1. и С2
9. Из условия существования ненулевого решения этой системы
приравнять нулю ее определителя.
10. Раскрыть определитель системы и получить уравнение частот.
11. Определить частоты собственных колебаний.
12. Формы собственных колебаний определяются ненулевым решением
Сj при k
где k
- одна из собственных частот.

5.

Пример 3. Определить собственную частоту продольных колебаний
стержневой системы
EF
М
с
c0
E
L
1. Уравнение
2. Решение
д 2u 1 д 2u
2 2 0 (8.2а )
2
дx c0 дt
u ( x, t ) U ( x) sin t
( 8.3а )
3. Подстановка (8.3а) в (8.2а) приводит к
уравнению
U U 0 (8.4) где
c0
2
(8.5)
4. Общее решение (8.4) можно представить в виде
U ( x ) C1 sin x C2 cos x
( 8.6)

6.

4. Общее решение (8.4) можно представить в виде
U ( x ) C1 sin x C2 cos x
5. Граничные условия
u (0, t) = 0
(x = 0)
( 8.6)
дu
д 2u
EF
M 2 cu
дx
дt
( x L)
7. Подставим (8.3a) в граничные условия
U (0) = 0
дU
EF
M ( 2 )U cU
дx
(x = 0)
8. Подставим (8.6) в граничные условия относительно U(x)
U ( 0) 0 C 2 0
U ( x) C1 sin x
( 8.6а )
дU
EF
M ( 2 )U cU ( x L)
дx
EFC1 cos L MC1 2 sin L cC1 sin L
9. Для того, чтобы было не нулевое решение необходимо
EF cos L ( M 2 c) sin L
( x L)

7.

EF cos L ( M 2 c) sin L
10. Преобразования
L
2
EF
( M c)tg
: M
E
c0
EF
M
c
L
(
)tg
E
M
c0
EF
M
c
L
(
)tg
E
M
c0
FL E
c
L
(
) Ltg
M
M
c0
FL
c
L
c0 (
) Ltg
M
M
c0
FL L
cL
L
(
)tg
M
c0 c0 M
c0
FL L 02 L L
tg
M
c0 c0 c0
02 L2 / c02
FL
tg
M

8.

11. Собственные частоты продольных колебаний определяются из уравнения
02 L2 / c02
FL
tg
M
12. Собственные формы продольных колебаний
k x
U k ( x) sin
(10.9)
c0