Колебания систем с одной степенью свободы

1.

Семинар 3. КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
Числом степеней свободы механической системы называется число
координат, определяющих ее положение.
Все реальные деформируемые тела обладают бесконечным числом
степеней свободы, соответствующих всевозможным их деформированным
состояниям.
Можно ограничить число учитываемых в расчете степеней свободы,
выбирая в качестве расчетной схемы реальной конструкции систему,
обладающую несколькими или даже одной степенью свободы.
Закономерности для систем с одной степенью свободы, имеют большое
значение, так как задачу о колебаниях системы с произвольным числом степеней
свободы часто удается свести к ряду задач о колебаниях систем с одной
степенью свободы

2.

Часто в реальной конструкции можно выделить массивные элементы,
деформацией которых можно пренебречь, и упругие элементы, массу которых
можно не учитывать.
Тема 1 Метод конечных
элементов
для
стержневых
элементов
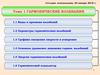
Система, представленная на рис.1, а, может рассматриваться как
система с одной степенью свободы, если масса пружины мала по сравнению с
массой груза.
Другим примером систем с одной степенью свободы может служить
диск, закрепленный на упругом валике (рис.1, б). Если масса вала пренебрежимо
мала по сравнению с массой диска, а диск может перемешаться только
поворачиваясь в своей плоскости вокруг оси вал.

3.

На рис. 2 представлены системы с двумя степенями свободы.
Тема 1 Метод конечных
элементов
для
стержневых
элементов
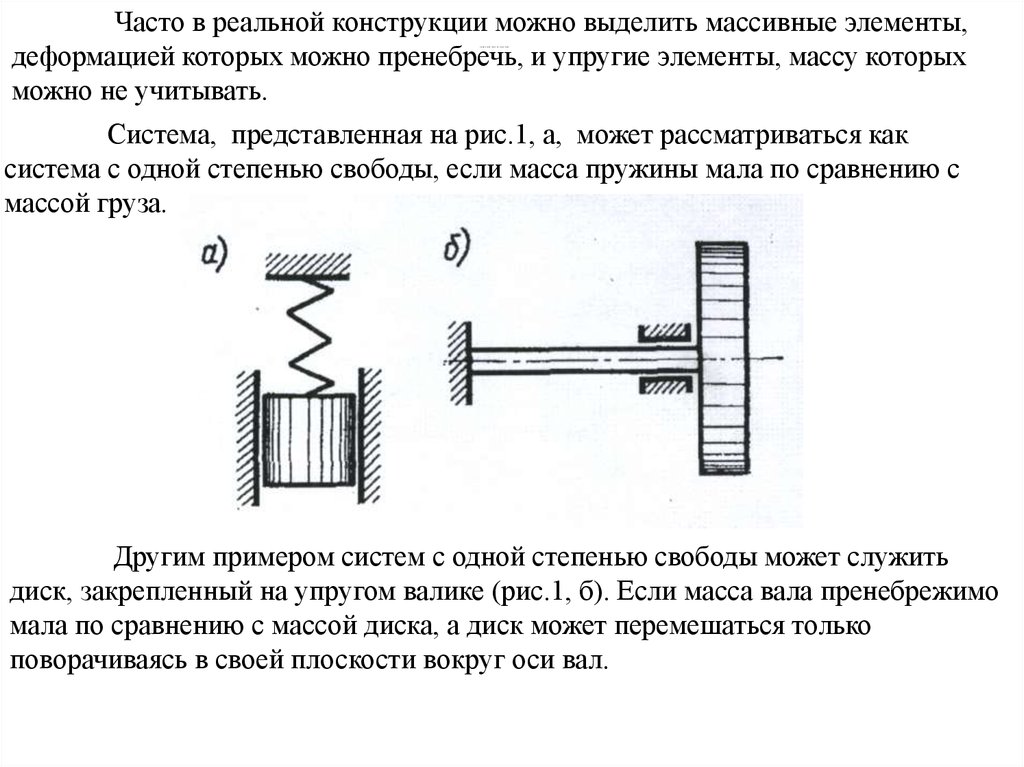
Положение грузов (рис.2,а), масса
которых значительно больше массы пружин,
при движении в вертикальном направлении
определяется двумя координатами: х1 и х2.

4.

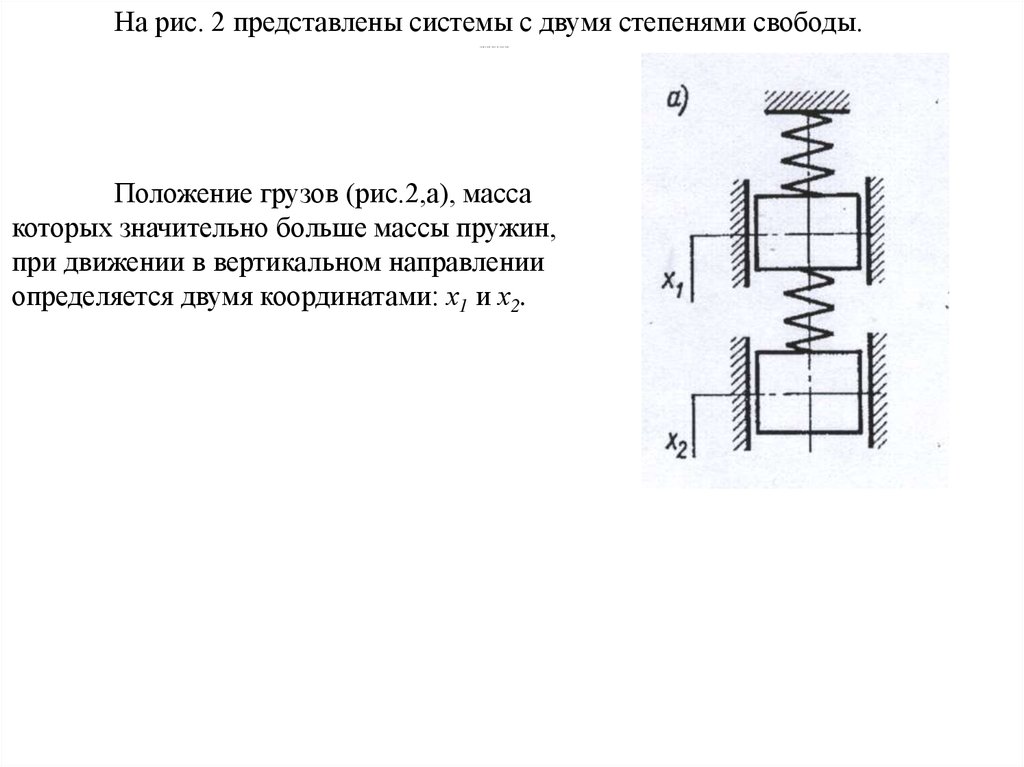
Системы, изображенные на рис.2, б, в, могут рассматриваться как
системы с двумя степенями свободы, если собственные массы балки и рамы малы
по сравнению с массой колеблющихся грузов, а размеры грузов невелики, так что
массы их можно считать сосредоточенными.
Тема 1 Метод конечных
элементов
для
стержневых
элементов
В случае больших поперечных размеров груза (рис.2,г) положение его
определяется смещением центра массы х1 и углом поворота груза х2. Такая
система имеет две степени свободы.

5.

Определение собственной частоты системы с одной степенью свободы
1. Записать кинетическую и потенциальную энергию системы соответственно
1
1 2
2
T m q , U k q
2
2
(3.1)
2. Подставить выражения для кинетической и потенциальной энергии в
уравнения Лагранжа 2-го рода
d дT
д
(
) (T U ) 0
dt дq
дq
3. Записать дифференциальное уравнение свободных колебаний, которое имеет
вид
k q 0 ( 3.2 )
mq
4. Записать решение дифференциального уравнения свободных колебаний в виде
гармонической функции
i t
q Ae
( 3.3 )

6.

5. Подставить решение в дифференциальное уравнение свободных колебаний
i t
( m k ) Ae
2
0
Условием не нулевого решения является равенство нулю определителя
алгебраической системы
2 m k 0 ( 3.4 )
6. Определить собственную частоту колебаний
12
k
m
( 3.5 )
Если ввести f = k -1 - единичную податливость, соответствующую
квазиупругому коэффициенту k.
1
mf
1
( 3.5 )
2

7.

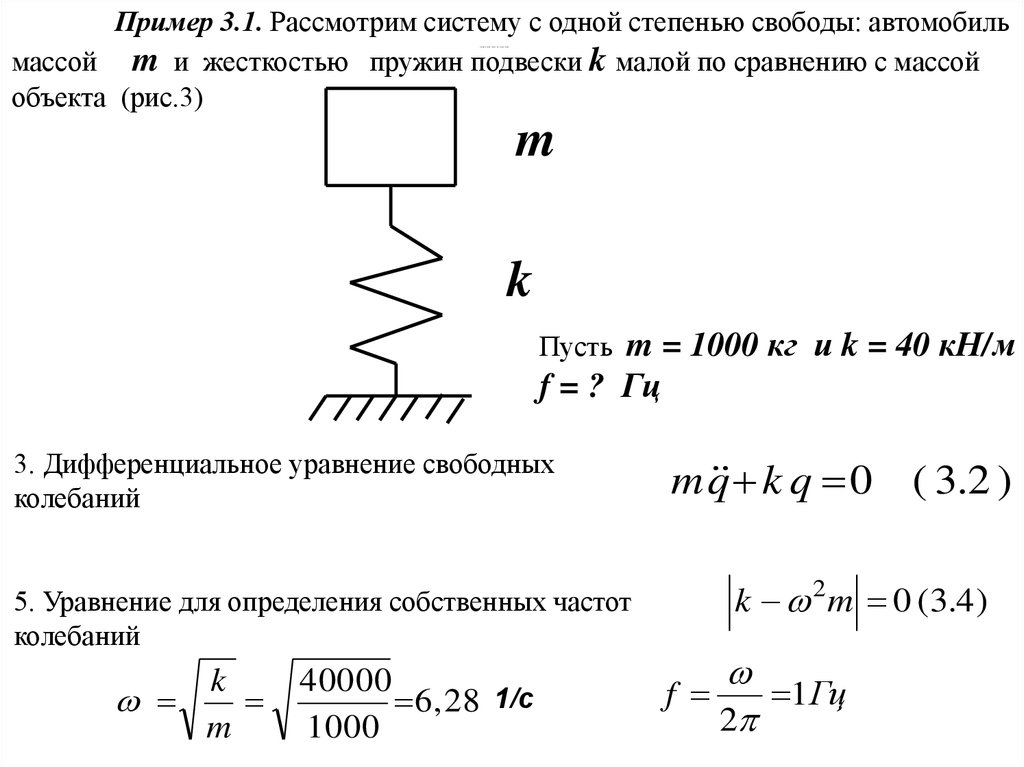
Пример 3.1. Рассмотрим систему с одной степенью свободы: автомобиль
массой m и жесткостью пружин подвески k малой по сравнению с массой
объекта (рис.3)
Тема 1 Метод конечных
элементов
для
стержневых
элементов
m
k
Пусть m = 1000 кг и k = 40 кН/м
f = ? Гц
3. Дифференциальное уравнение свободных
колебаний
5. Уравнение для определения собственных частот
колебаний
k
m
40000
6 , 28 1/с
1000
k q 0 ( 3.2 )
mq
k 2 m 0 ( 3.4 )
f
1 Гц
2

8.

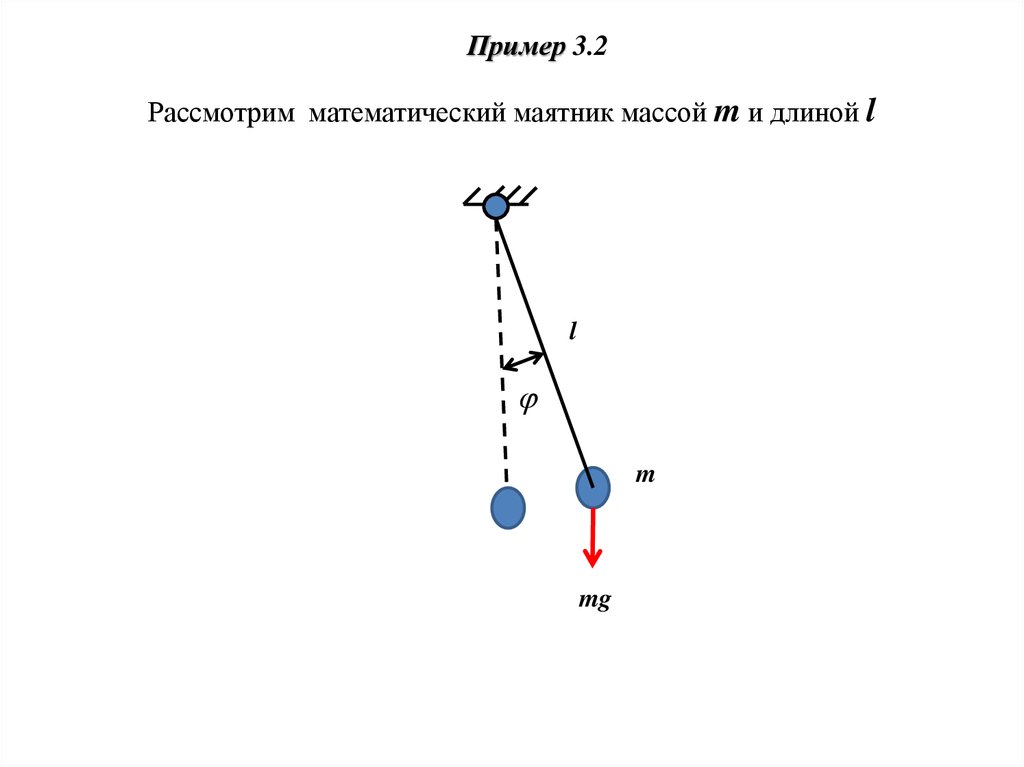
Пример 3.2
Рассмотрим математический маятник массой m и длиной l
l
m
mg

9.

Математический маятник Фуко в
Национальном соборе г. Мехико

10.

1. Кинетическая и потенциальная энергия для математического маятника массой
m и длиной l :
1 2 2
1
T m l , U mgl 2
2
2
2. Подставить выражения для кинетической и потенциальной энергии в
уравнения Лагранжа 2-го рода
d дT
д
(
) (T U ) 0
dt дq
дq
3. Дифференциальное уравнение свободных колебаний маятника имеет вид
ml mgl 0
2
- угол наклона маятника относительно положения равновесия
4. Решение дифференциального уравнения
i t
Ae
5. Подставить решение в дифференциальное уравнение и приравнять
определитель нулю
2
l g 0 ( 3.4 )

11.

Вычисляем собственную частоту свободных колебания маятника
12
g
l
( 3.6 )
Пусть l = 98,1 м
12
9 ,81
98,1
f = 0,05 Гц
0 , 311428 1 / с
Т= 20 с

12.

Тема 1 Метод конечных
элементов
для
стержневых
элементов
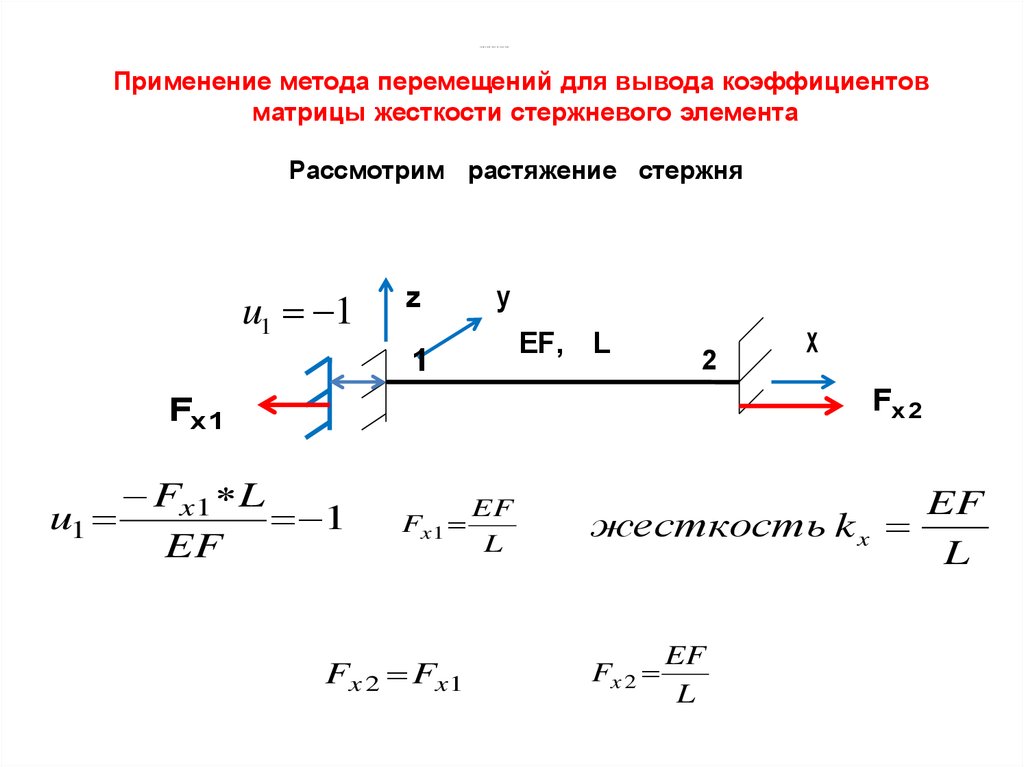
Применение метода перемещений для вывода коэффициентов
матрицы жесткости стержневого элемента
Рассмотрим растяжение стержня
u1 1
z
y
EF, L
1
2
x
Fx 2
Fx 1
Fx1 L
u1
1
EF
Fx1
Fx 2 Fx 1
EF
L
EF
жесткость k x
L
Fx 2
EF
L

13.

Пример 3.3. Рассмотрим продольные колебания стержня с массой М
на конце
Тема 1 Метод конечных
элементов
для
стержневых
элементов
u
L = 2 м, сечение прямоугольное шириной b = 5 см и высотой h = 3 см,
Е = 200 000 Мпа, М = 50 кг
1
1 2
2
T m u , U k u
2
2
Уравнение для определения собственных частот колебаний
k 2m 0

14.

Уравнение для определения собственных частот колебаний
k 2m 0
L = 2 м, сечение прямоугольное шириной b = 5 см и высотой h = 3 см,
Е = 200 000 Мпа, М = 50 кг
EF
2 1011 15 10 4
kx
15 107
L
2
k
15 107
1, 7 103 1/с
m
50
f
Н/м
270 Гц
2

15.

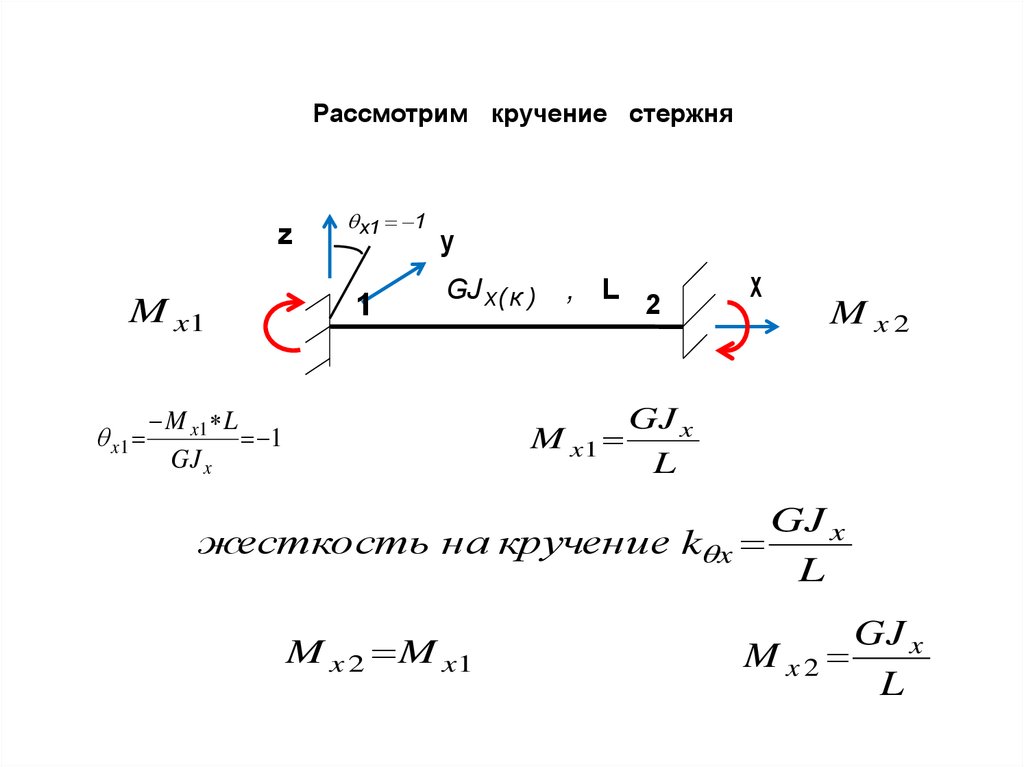
Рассмотрим кручение стержня
z
M x1
x1
x1 1
1
y
GJ x( к )
M x1 L
1
GJ x
, L
M x1
2
x
M x2
GJ x
L
GJ x
жесткость на кручение k x
L
M x 2 M x1
GJ x
M x2
L

16.

Пример 3.4. Рассмотрим крутильные колебания вала с диском на конце
с моментом инерции Iх
Тема 1 Метод конечных
элементов
для
стержневых
элементов
Iх = MR2 /2
x
L = 2 м, сечение круглое d = 4 см, G = 80 000 Мпа, М = 50 кг, R=20 см
1
1
2
T I x , U k x 2
2
2
Уравнение для определения собственных частот колебаний
k x 2 I x 0

17.

Уравнение для определения собственных частот колебаний
k x 2 I x 0
L = 2 м, сечение круглое d = 4 см, G = 80 000 Мпа, М = 50 кг, R=20 см
k x
GJ x 8 101 0 3,14 4 4 108
104
L
2 32
Iх = MR2 /2 = 50*0,04/2 = 1
k x
100 1/с
Ix
кг* м2
f
16, 6 Гц
2
Н*м