Similar presentations:
Вынужденные колебания системы с одной степенью свободы
1. Лекция 5-6. Вынужденные колебания системы с одной степенью свободы
Содержание1.
Действие
гармонической
нагрузки с учетом и без учета сил
сопротивления.
2.
Действие
произвольной
возмущающей нагрузки.
3. Динамический коэффициент.
2. Вынужденные колебания системы с одной степенью свободы
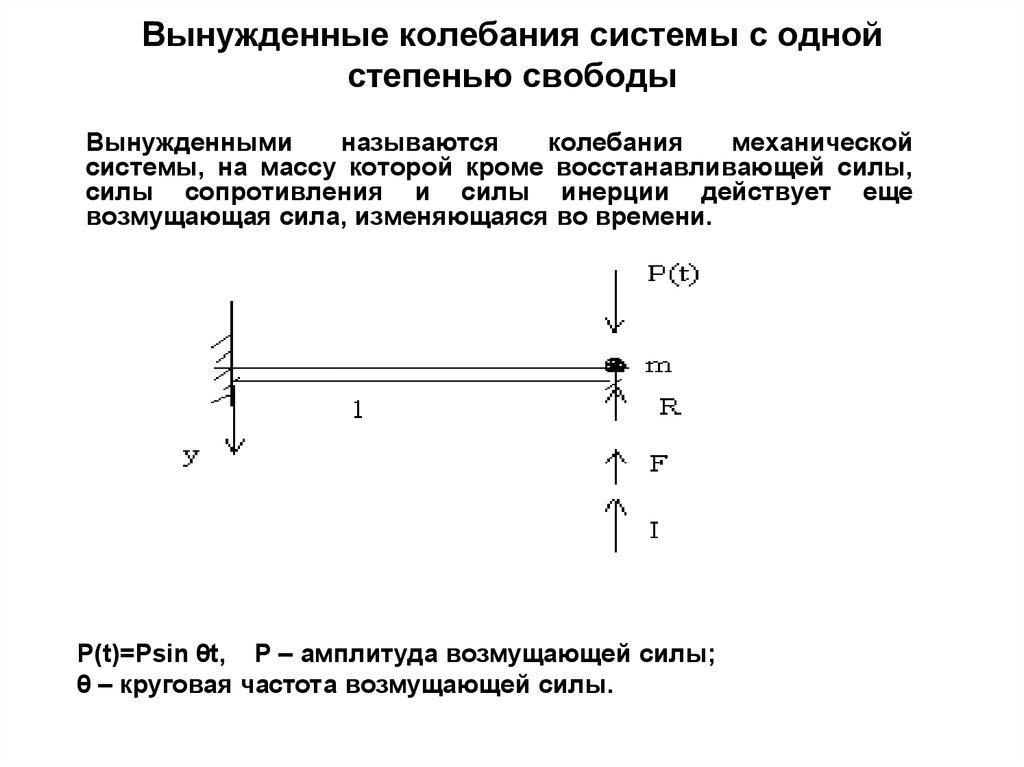
Вынужденныминазываются
колебания
механической
системы, на массу которой кроме восстанавливающей силы,
силы сопротивления и силы инерции действует еще
возмущающая сила, изменяющаяся во времени.
P(t)=Psin θt, Р – амплитуда возмущающей силы;
θ – круговая частота возмущающей силы.
3. Уравнение динамического равновесия
Y0,
R F I P (t ),
k /
r
P
y
y
y
Sin t ,
m
m
m
y y o yч ,
//
y ao e
kt
2m
Sin ( t o ) yст Sin ( t )
ε – сдвиг фазы вынужденных колебаний по отношению к
колебаниям возмущающей силы, характеризующий величину
опережения
k
arctg 2m 2
4. Формула для динамического коэффициента
• μ – динамический коэффициент гармонической нагрузки,показывающий во сколько раз ее динамическое действие
превышает статическое действие ее амплитуды
1
k 2
(1 2 ) 2 (
)
2
m
2
1
2 2
2
(1 2 ) (
)
,
k
коэффициен т
сопротивления,
m
2
T
период
собственных
колебаний ,
2
T
период
вибрационной
нагрузки .
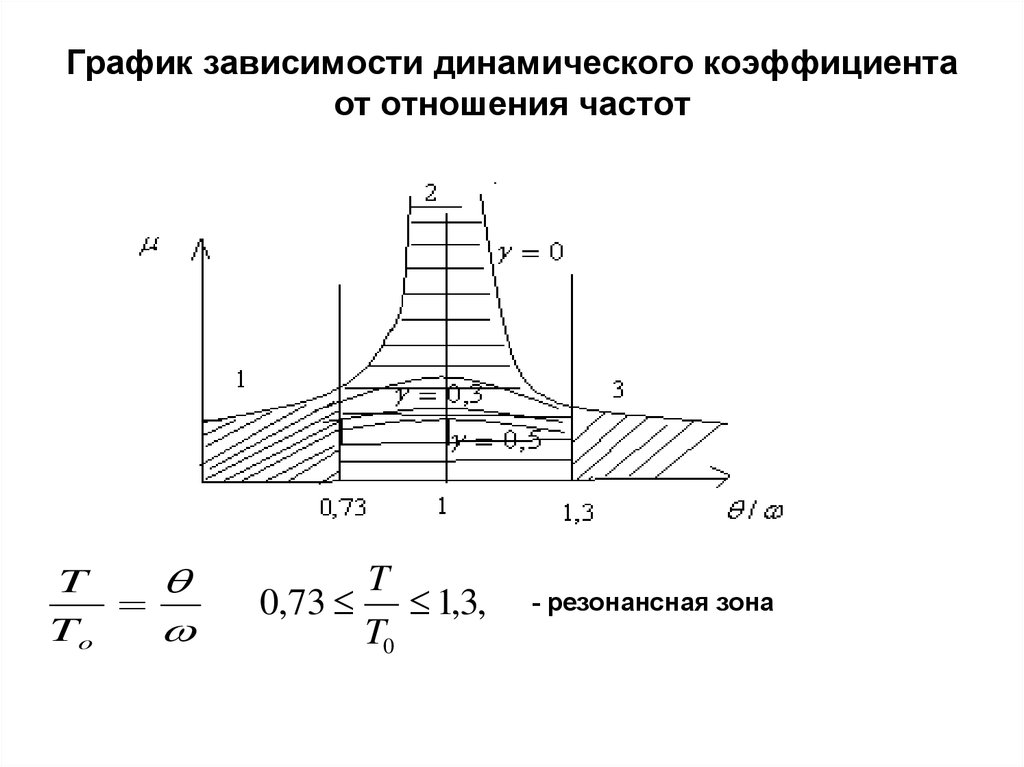
5. График зависимости динамического коэффициента от отношения частот
TTo
T
0,73 1,3,
T0
- резонансная зона



 physics
physics








