Similar presentations:
Знакомая незнакомка. Парабола
1.
Да, путь познания не гладокНо знаем мы со школьных лет:
Загадок больше чем разгадок,
И поискам предела нет !
2.
Решение неравенстввторой степени с одной
переменной, используя график
квадратичной функции
3.
Работаем устно4.
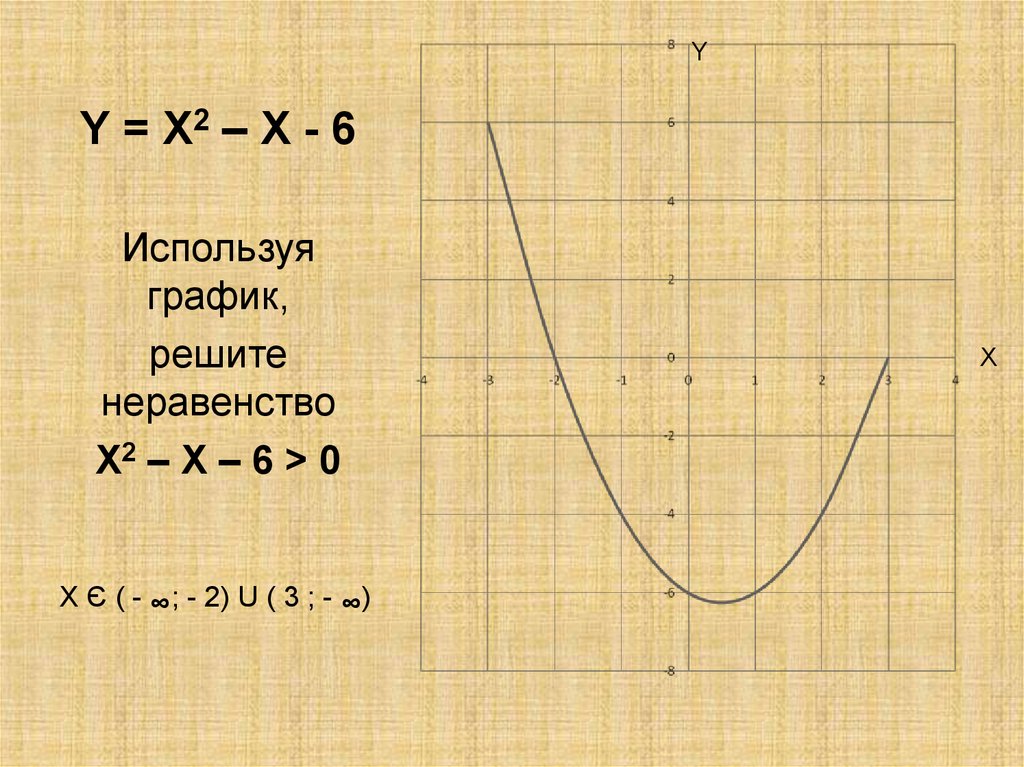
YY = X2 – X - 6
Используя
график,
решите
неравенство
X2 – X – 6 > 0
X Є ( - ∞; - 2) U ( 3 ; - ∞)
X
5.
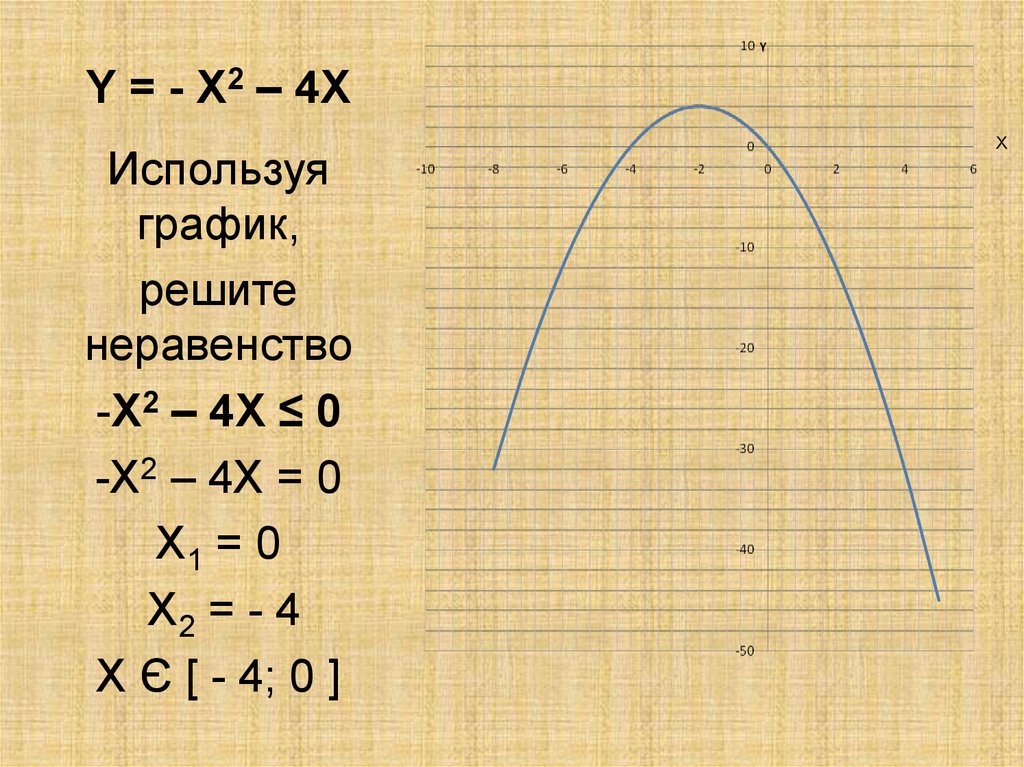
Y = - X2 – 4XИспользуя
график,
решите
неравенство
-X2 – 4X ≤ 0
-X2 – 4X = 0
X1 = 0
X2 = - 4
X Є [ - 4; 0 ]
X
6.
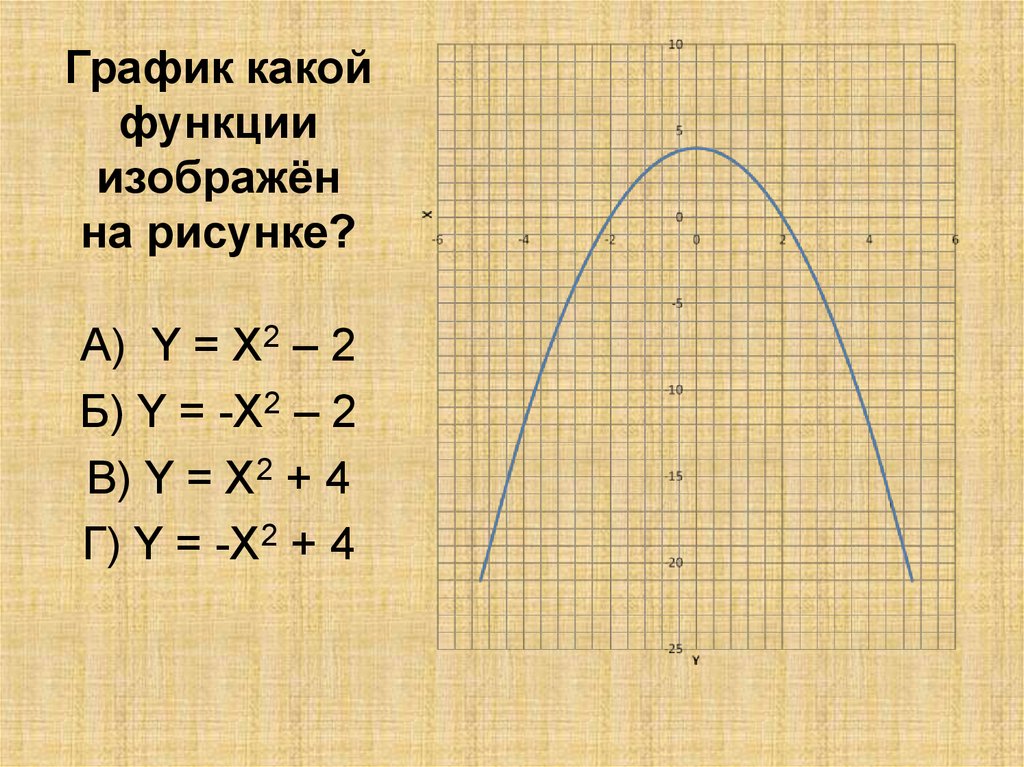
График какойфункции
изображён
на рисунке?
А) Y = X2 – 2
Б) Y = -X2 – 2
В) Y = X2 + 4
Г) Y = -X2 + 4
7.
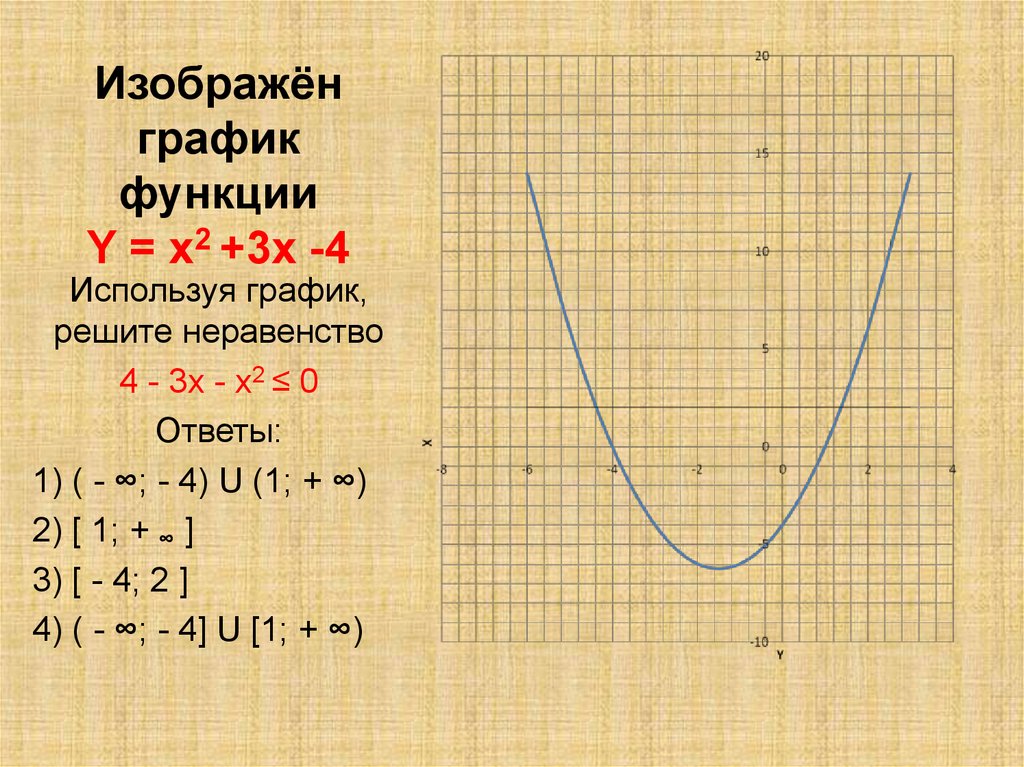
Изображёнграфик
функции
Y = х2 +3х -4
Используя график,
решите неравенство
4 - 3х - х2 ≤ 0
Ответы:
1) ( - ∞; - 4) U (1; + ∞)
2) [ 1; + ∞ ]
3) [ - 4; 2 ]
4) ( - ∞; - 4] U [1; + ∞)
8.
Проверь себя9.
Проверь себя1 вариант
1. X2 –5X + 6 < 0
2. 2X2 +4X + 1 > 0
3. -X2 +2X ≤ 0
4. 4X2 –12X + 9 ≤ 0
5. Найти область
определения
функции
Y = 2x − 5x− 3
2
2 вариант
1. X2 –3X + 2 > 0
2. -X2 -3X < 0
3. 9X2 +6X-1 ≥ 0
4. 3X2 –7X + 2 ≤ 0
5. Найти область
определения
функции
Y=
x2
1
x− 2
10.
Проверь себя сам и оцени1 вариант
2 вариант
1. X Є ( 2; 3)
2. X Є (- ∞; + ∞)
3. X Є [ 0; 2 ]
4. Решений нет
5. X Є ( - ∞; - ½) U (3; + ∞)
1. X Є ( - ∞; 1) U (2; + ∞)
2. X Є ( - ∞; 0) U (3; + ∞)
3. Х ≠ ⅓
4. X Є [½; 2 ]
5. X Є ( - ∞; - 2) U (1; + ∞)
11.
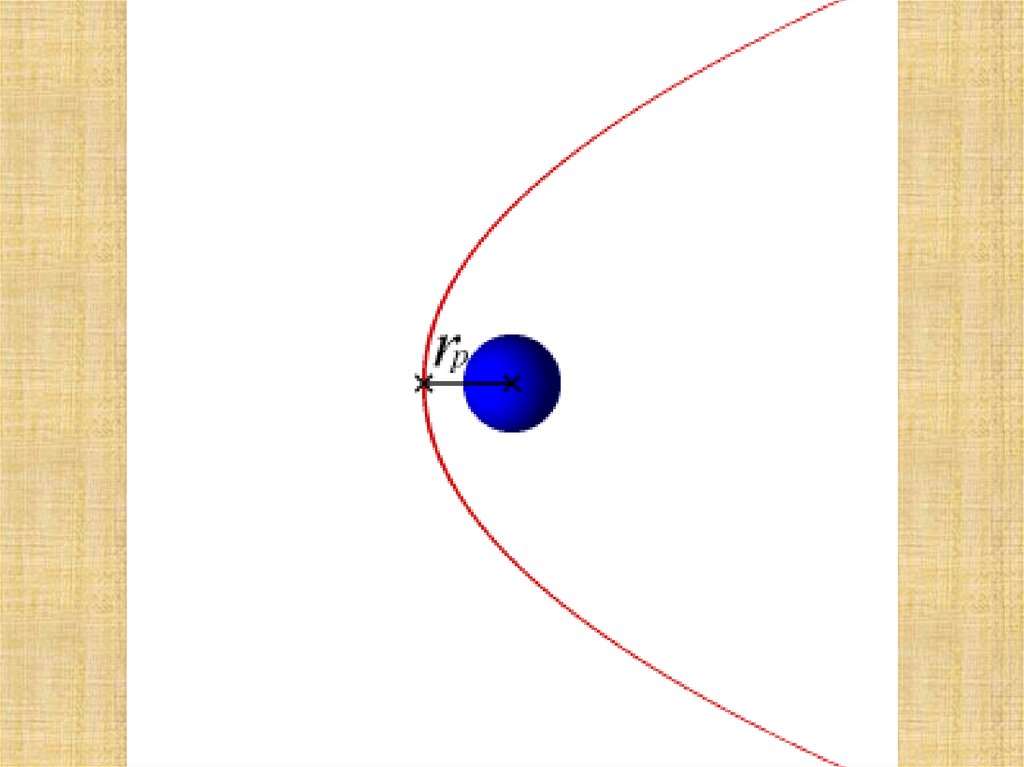
Знакомая незнакомка12.
13.
14.
15.
16.
Спасибо за работу!Учитель математики МОУ СОШ №1г.Кемь
Людмила Михайловна Давлюдова











 mathematics
mathematics








