Парабола прямая. Часть II

1.

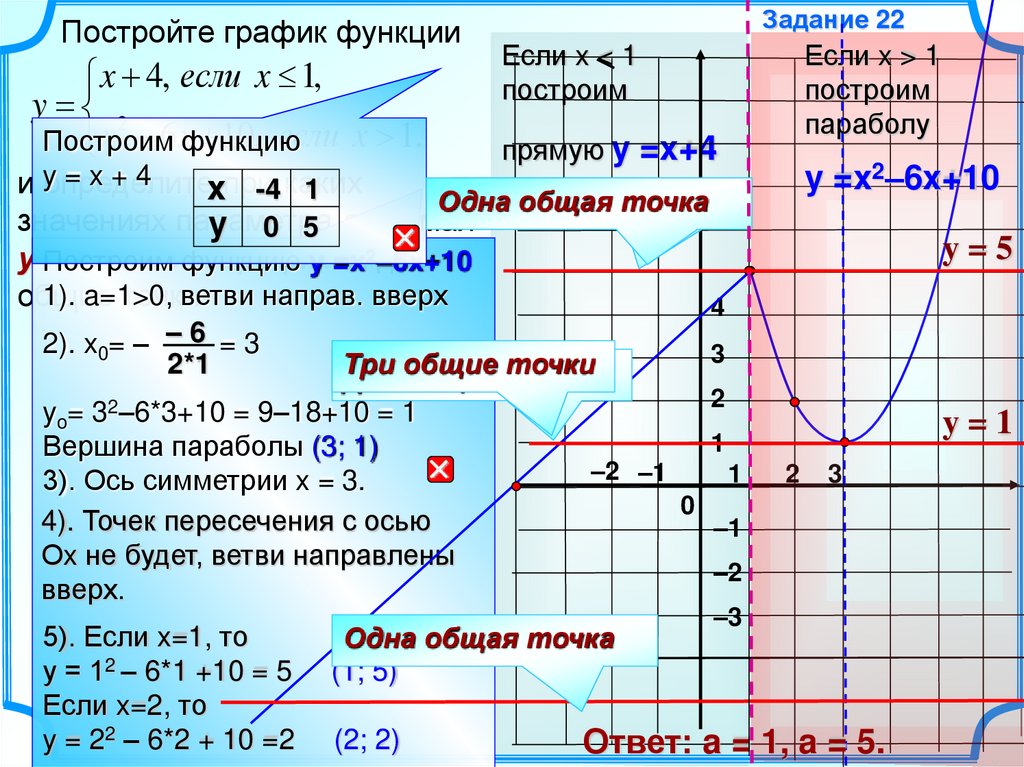
Постройте график функции
x 4, если x 1,
y 2
10, если x 1.
Построим
x 6 xфункцию
Задание 22
Если x < 1
построим
Если x > 1
построим
параболу
прямую y =x+4
y =x2–6x+10
=x+4
и yопределите
-4 каких
1
xпри
Одна
Две общая
общие точка
точки
значениях параметра
а
прямая
y 0 5
2
у Построим
= а имеетфункцию
с графиком
две
y =x –6x+10
1). a=1>0,
ветви направ. вверх
общие
точки
4
y=5
2). x0= – – 6 = 3
2*1
3
Три
общие
точки
Две общие точки
2
yo= 32–6*3+10 = 9–18+10 = 1
1
Вершина параболы (3; 1)
–2 –1
1
3). Ось симметрии x = 3.
0
4). Точек пересечения с осью
–1
Оx не будет, ветви направлены
–2
вверх.
5). Если x=1, то
у = 12 – 6*1 +10 = 5
Если x=2, то
y = 22 – 6*2 + 10 =2
Одна общая точка
(1; 5)
(2; 2)
y=1
2
3
–3
Ответ: a = 1, a = 5.

2.

Задание 22
Если x < –3
Постройте график функции
построим прямую
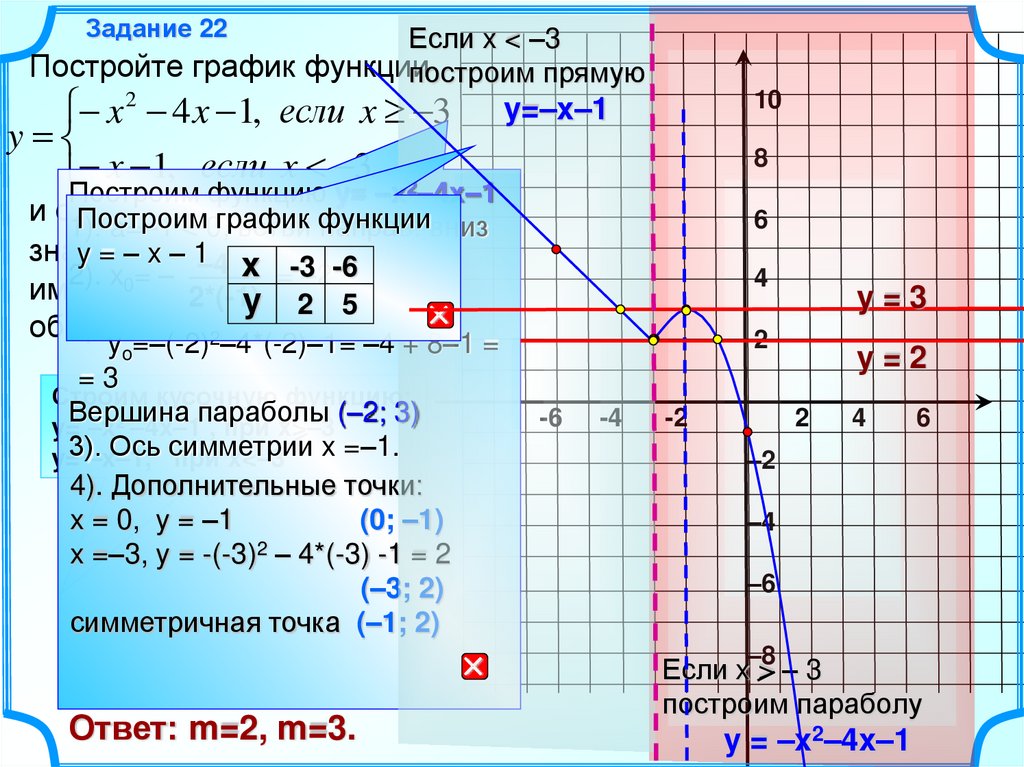
x 2 4 x 1, если x 3 y=–x–1
y
x 1, если x 3 2
Построим
функцию y= –x –4x–1
10
=
8
и определите,
при каких
Построим
1).
a=–1 < 0,график
ветви функции
направ. вниз
значениях
y=m
y = – x –m
1–4прямая
-3
-6
x
2). x0= –
= –2
имеет
с графиком
две
2*(-1)
y 2ровно
5
общие точки.2
yo=–(-2) –4*(-2)–1= –4 + 8–1 =
=3
Строим кусочную функцию:
Вершина параболы (–2; 3)
y= –x2 –4x–1 , при x>–3
Ось симметрии
y=3).
–x–1,
при x<–3 x =–1.
4). Дополнительные точки:
x = 0, y = –1
(0; –1)
x =–3, y = -(-3)2 – 4*(-3) -1 = 2
(–3; 2)
симметричная точка (–1; 2)
Ответ: m=2, m=3.
6
4
y=3
2
-6
-4
-2
y=2
2
4
6
–2
–4
–6
–8
Если x > – 3
построим параболу
y = –x2–4x–1

3.

Если x < 0
Если x > 0
построим параболу построим прямую
Постройте график
функции
Одна общая точка
Две общие
точки !
y =x2+3x+7
y = 7–x
Задание 22
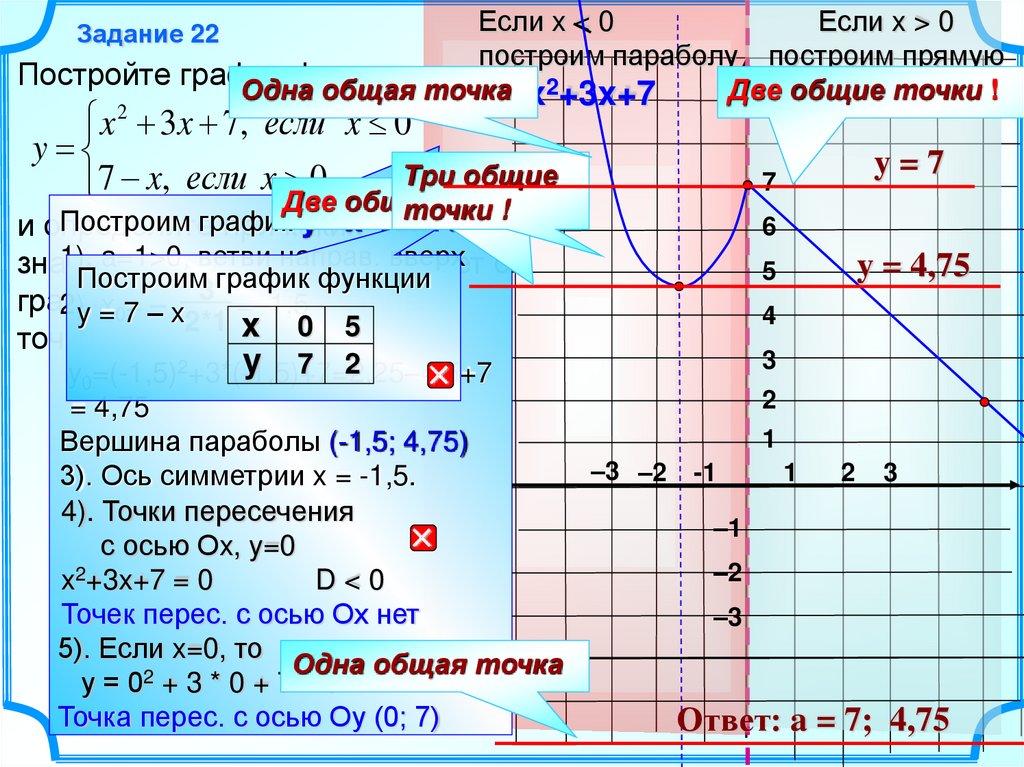
x 2 3x 7, если x 0
y
Три общие
0
7 x, если x Две
общие точки !
точки !
Построим график
y =x2+3x+7
и определите
при каких
1). a=1>0,
ветви
направ.
вверх
значениях
a
прямая
y
=
a
имеет с
Построим3график функции
графиком
две общие
2).
x07= –– ровно
y=
x2*1 =–1,5
x 0 5
точки.
7
y=7
6
5
y = 4,75
4
3
y 7 2
y0=(-1,5)2+3*(-1,5)+7=2,25–4,5+7
2
= 4,75
1
Вершина параболы (-1,5; 4,75)
–3 –2 -1
1
2 3
3). Ось симметрии x = -1,5.
4). Точки пересечения
–1
с осью Оx, y=0
–2
x2+3x+7 = 0
D<0
Точек перес. с осью Ох нет
–3
5). Если x=0, то
Одна общая точка
у = 02 + 3 * 0 + 7 = 7
Точка перес. с осью Оу (0; 7)
Ответ: a = 7; 4,75

4.

Задание 22
Если x > –1
построим параболу
Постройте график функции
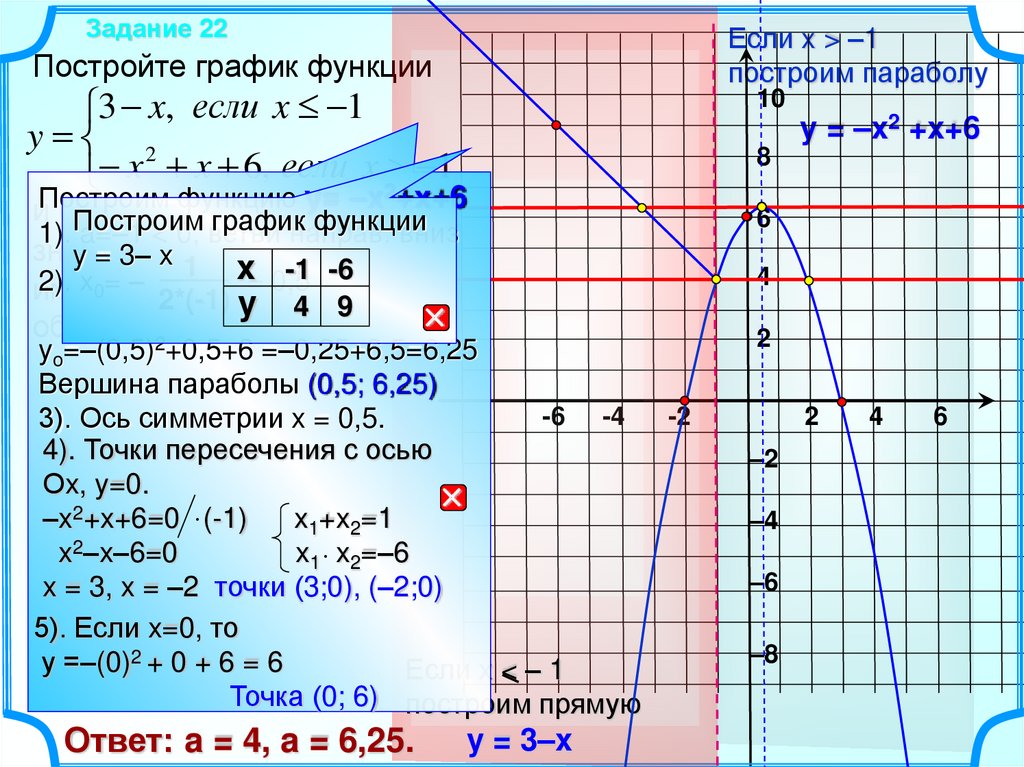
3 x, если x 1
y 2
x x 6, если x 2 1
10
8
функцию
y=
–x +x+6
иПостроим
определите,
при
каких
график
функции
1).Построим
a=–1 < 0, ветви
направ.
вниз
значениях
y=a
y = 3– x 1a прямая
-1
-6
x
2). x0= с
– графиком
= 0,5
имеет
две
2*(-1) y 4ровно
9
общие точки.
2
yo=–(0,5) +0,5+6 =–0,25+6,5=6,25
Вершина параболы (0,5; 6,25)
-6 -4
-2
3). Ось симметрии x = 0,5.
4). Точки пересечения с осью
Оx, y=0.
–x2+x+6=0 (-1)
x1+x2=1
x2–x–6=0
x1 x2=–6
x = 3, x = –2 точки (3;0), (–2;0)
5). Если x=0, то
у =–(0)2 + 0 + 6 = 6
Если x < – 1
Точка (0; 6) построим прямую
Ответ: a = 4, a = 6,25.
y = –x2 +x+6
y = 3–x
6
4
2
2
–2
–4
–6
–8
4
6

5.

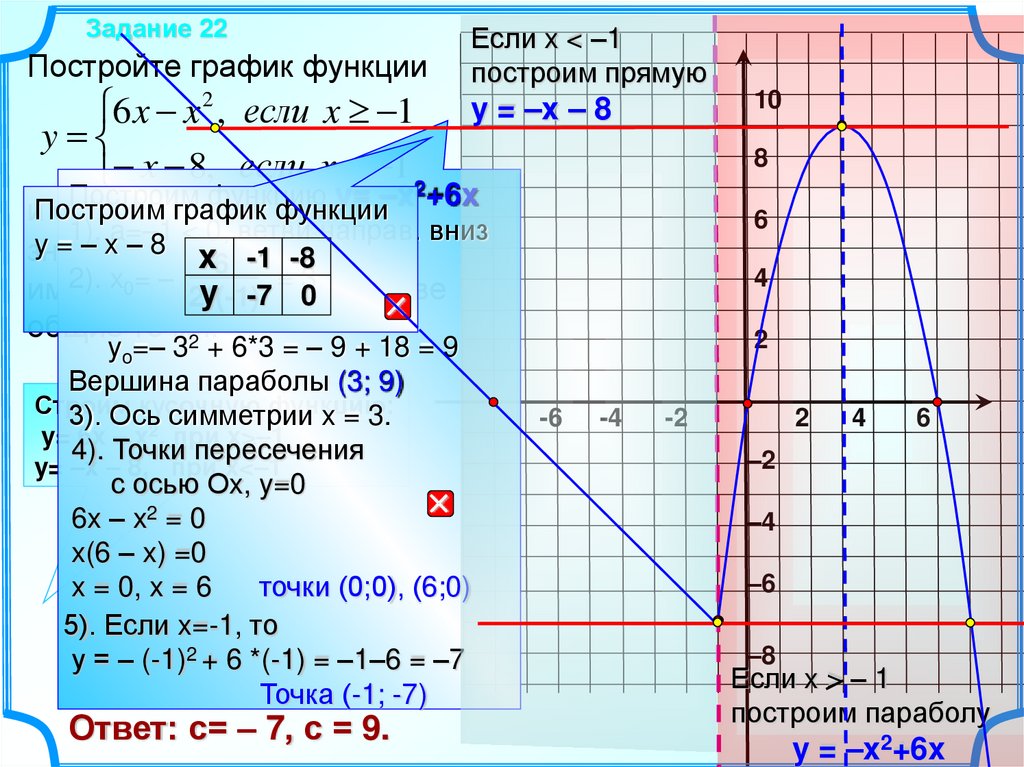
Задание 22
Постройте график функции
6 x x 2 , если x 1
y
x 8, если x 1 2
Если x < –1
построим прямую
10
y = –x – 8
8
Построим функцию y= –x +6x
график
функции
иПостроим
определите,
при
каких
1).
a=–1
< 0, ветви направ. вниз
y
=
–
x
–
8
значениях cx6
прямая
-1 -8 y=с
2). xс
–
= ровно
3
0=графиком
имеет
y
-7
0
2*(-1)
две
общие точки.
2
yo=– 3 + 6*3 = – 9 + 18 = 9
Вершина параболы (3; 9)
Строим
кусочную
функцию:
3). Ось
симметрии
x = 3.
2
y= 6x – x , при x>–1
4). Точки пересечения
y= –x – 8, при x<–1
с осью Оx, y=0
6x – x2 = 0
x(6 – x) =0
x = 0, x = 6
точки (0;0), (6;0)
5). Если x=-1, то
у = – (-1)2 + 6 *(-1) = –1–6 = –7
Точка (-1; -7)
Ответ: с= – 7, с = 9.
6
4
2
-6
-4
-2
2
4
6
–2
–4
–6
–8
Если x > – 1
построим параболу
y = –x2+6x

6.

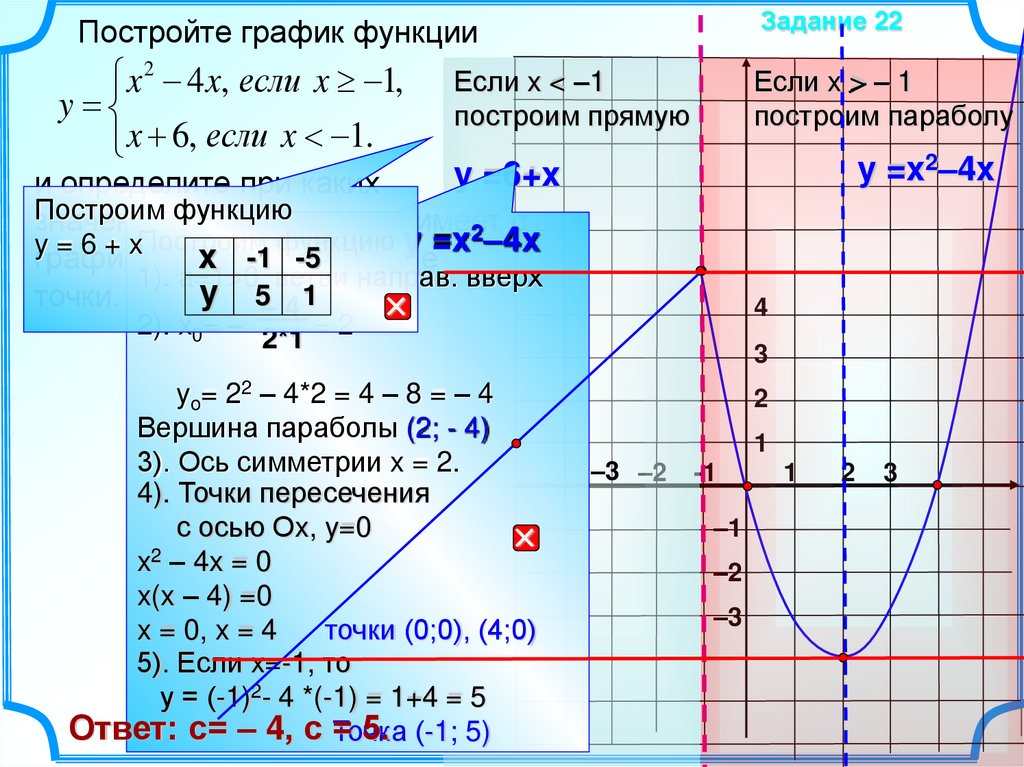
Задание 22
Постройте график функции
x 2 4 x, если x 1,
y
x 6, если x 1.
Если x < –1
построим прямую
Если x > – 1
построим параболу
y =x2–4x
y =6+x
и определите при каких
Построим
значенияхфункцию
с прямая y = с имеет
с
2
y =x –4x
y = 6 + xПостроим
-5 общие
x -1 функцию
графиком ровно
две
1). a=1>0, ветви направ. вверх
y 5– 4 1
точки.
4
2). x0= – 2*1 = 2
yo= 22 – 4*2 = 4 – 8 = – 4
Вершина параболы (2; - 4)
3). Ось симметрии x = 2.
4). Точки пересечения
с осью Оx, y=0
2
x – 4x = 0
x(x – 4) =0
x = 0, x = 4
точки (0;0), (4;0)
5). Если x=-1, то
у = (-1)2- 4 *(-1) = 1+4 = 5
Ответ: с= – 4, с =
5. (-1; 5)
Точка
3
2
–3 –2
1
-1
–1
–2
–3
1
2
3

7.

Постройте график функции
x 4 x 5, если x 1,
y
2 x, если x 1.
2
и Построим
определите
при каких
функцию
y = 2x
значениях
параметра
x -1 1 m прямая
у = m имеет yс графиком
две
-2 2
общие точки.
Задание 22
Если x < 1
построим
прямую y =2x
Одна общая точка
Построим график функции Две общие точки
y =x2–4x+5. ИспользуемТри
алгоритм
общие точки
выделения квадрата двучлена:
у
=(х2–4х
+5)– 4
+4
=(х–2)2+1
y =(x–2)2+1
4
3
y=2
y=1
2
1
–2 –1
Две общие точки
у=(х–2)2+1
Дополнительные точки.
Если x=0, то
у = 02 – 4*0 +5 = 5
(0;Одна
5) общая точка
Если x=1, то
y = 12 – 4*1 + 5 = 2 (1; 2)
Ответ: m = 1, m = 2.
Если x > 1
построим
параболу
1
0
–1
–2
–3
2
3

8.

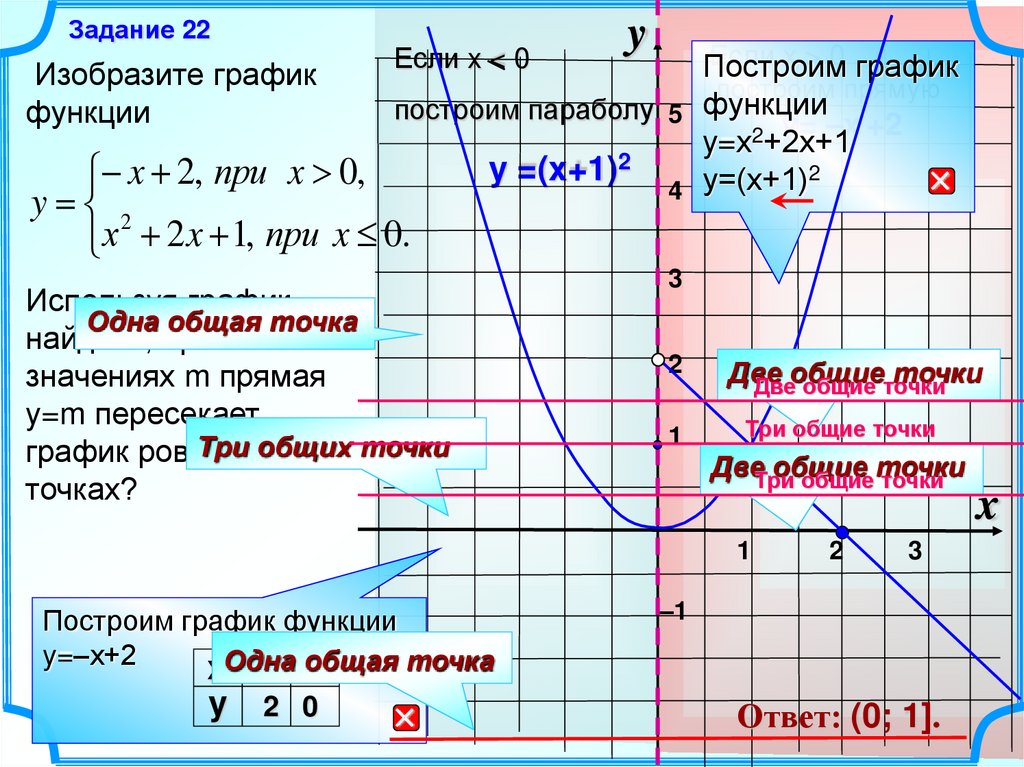
Задание 22
Изобразите график
функции
y
Если x > 0 график
Построим
построим прямую
функции
построим параболу 5
y= –x +2
y=х2+2х+1
y =(x+1)2
2
у=(х+1)
4
Если x < 0
x 2, при x 0,
y 2
х 2 x 1, при x 0.
Используя график,
Одна общая точка
найдите, при каких
значениях m прямая
y=m пересекает
Три
график ровно
в общих
трёх точки
точках?
3
2
1
Две
общие точки
Две общие точки
Три общие точки
ДвеТри
общие
точки
общие точки
1
Построим график функции
y=–х+2
точка
0 общая
2
xОдна
y
2 0
2
3
–1
Ответ: (0; 1].
x

9.

Задание 22
x < –2
Одна общаяЕсли
точка
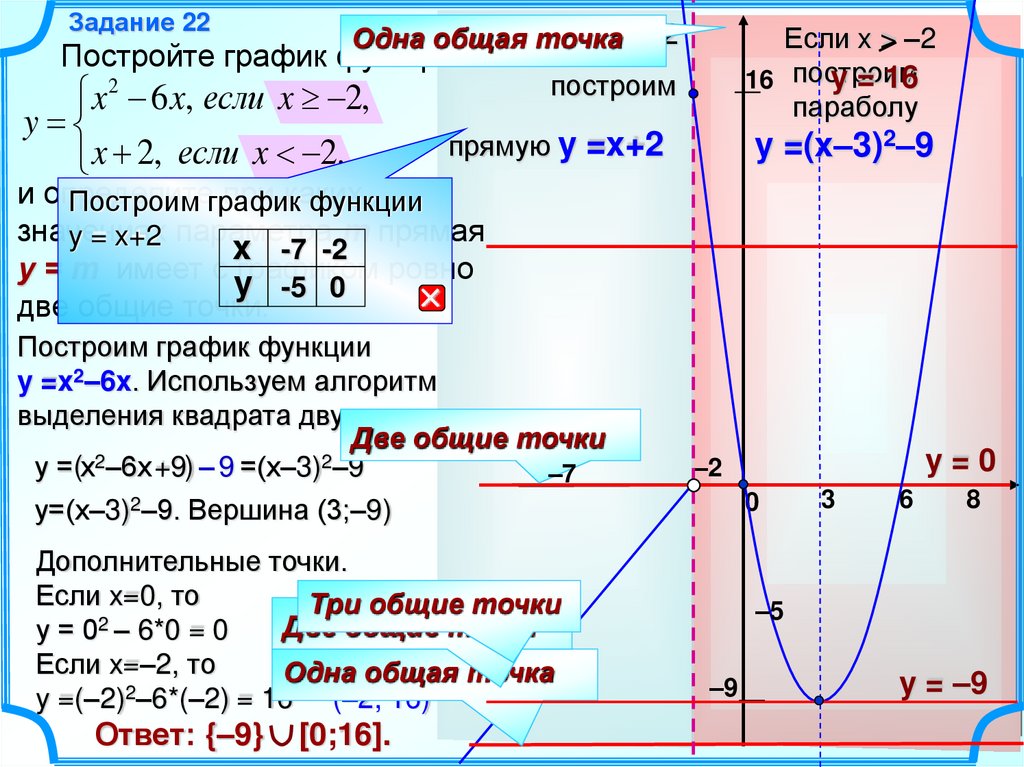
Постройте график функции
x 2 6 x, если x 2,
y
x 2, если x 2.
Если x > –2
y = 16
16 построим
параболу
построим
y =(x–3)2–9
прямую y =x+2
и определите
при каких
Построим график
функции
значениях
m прямая
y = x+2 параметра
x -7 -2
у = m имеет с графиком ровно
y -5 0
две общие точки.
Построим график функции
y =x2–6x. Используем алгоритм
выделения квадрата двучлена:
Две общие точки
у =(х2–6х +9) – 9 =(х–3)2–9
–7
у=(х–3)2–9. Вершина (3;–9)
Дополнительные точки.
Если x=0, то
Три общие точки
2
Две
у = 0 – 6*0 = 0
(0;
0) общие точки
Если x=–2, то
Одна общая точка
2
y =(–2) –6*(–2) = 16 (–2; 16)
Ответ: {–9}
[0;16].
y=0
–2
0
3
6
8
–5
–9
y = –9

10.

Задание 22
Если x < –1
Если x > –1
построим
параболу
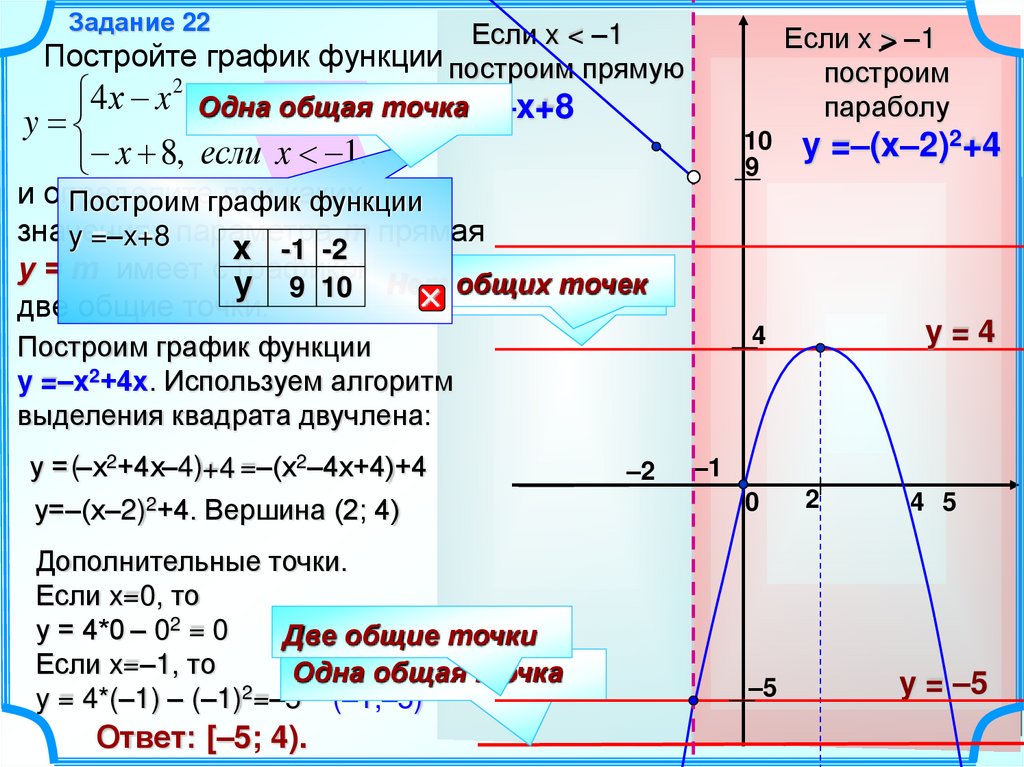
Постройте график функции построим прямую
4 х x 2 , Одна
если общая
x 1, точка
y =–x+8
y
x 8, если x 1.
и определите
при каких
Построим график
функции
значениях
m прямая
y =–x+8 параметра
x -1 -2
у = m имеет с графиком Нет
ровно
общих
y 9 10 Одна
общая точек
точка
две общие точки.
Построим график функции
y =–x2+4х. Используем алгоритм
выделения квадрата двучлена:
у = (–х2+4х–4)+4 =–(х2–4х+4)+4
у=–(х–2)2+4. Вершина (2; 4)
Дополнительные точки.
Если x=0, то
у = 4*0 – 02 = 0
(0;
0) общие точки
Две
Если x=–1, то
Одна общая точка
2
y = 4*(–1) – (–1) =–5 (–1;–5)
Ответ: [–5; 4).
–2
10
9
y =–(x–2)2+4
4
y=4
–1
0
–5
2
4 5
y = –5