Similar presentations:
Парабола. Часть II
1.
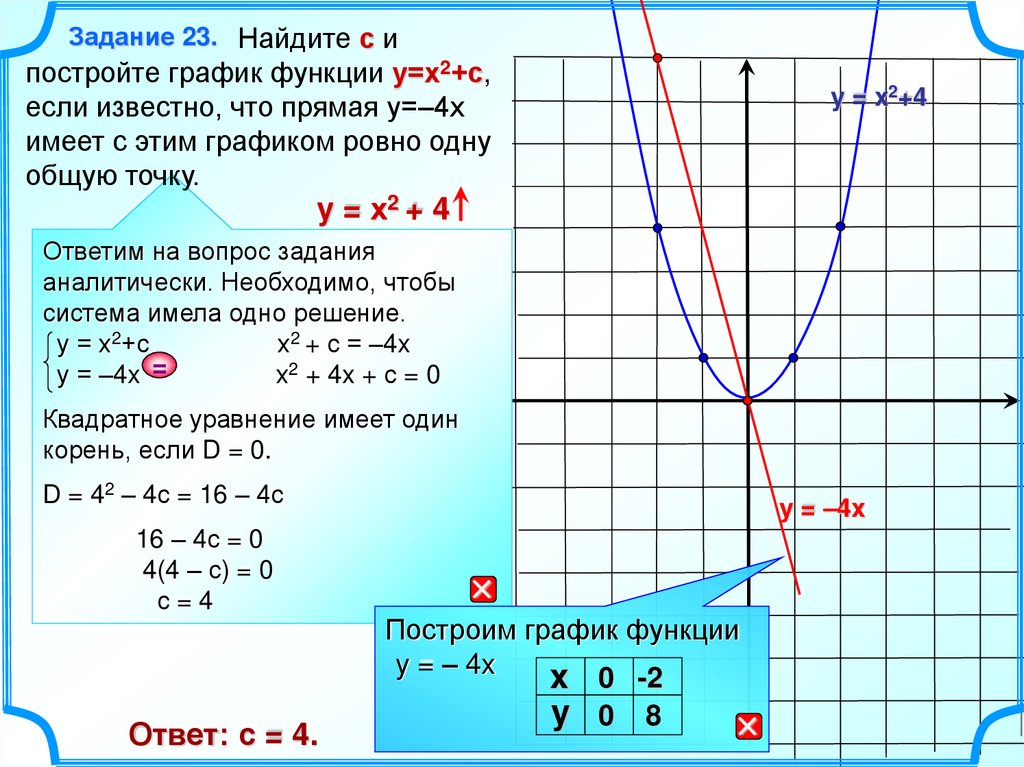
Задание 23. Найдите с ипостройте график функции у=х2+с,
если известно, что прямая у=–4х
имеет с этим графиком ровно одну
общую точку.
y = x2+4
y = х2 + 4
Ответим на вопрос задания
аналитически. Необходимо, чтобы
система имела одно решение.
у = х2+с
х2 + с = –4x
у = –4x =
х2 + 4x + с = 0
Квадратное уравнение имеет один
корень, если D = 0.
D = 42 – 4с = 16 – 4с
16 – 4с = 0
4(4 – с) = 0
с=4
Ответ: с = 4.
y = –4x
Построим график функции
y = – 4x
x 0 -2
y 0 8
2.
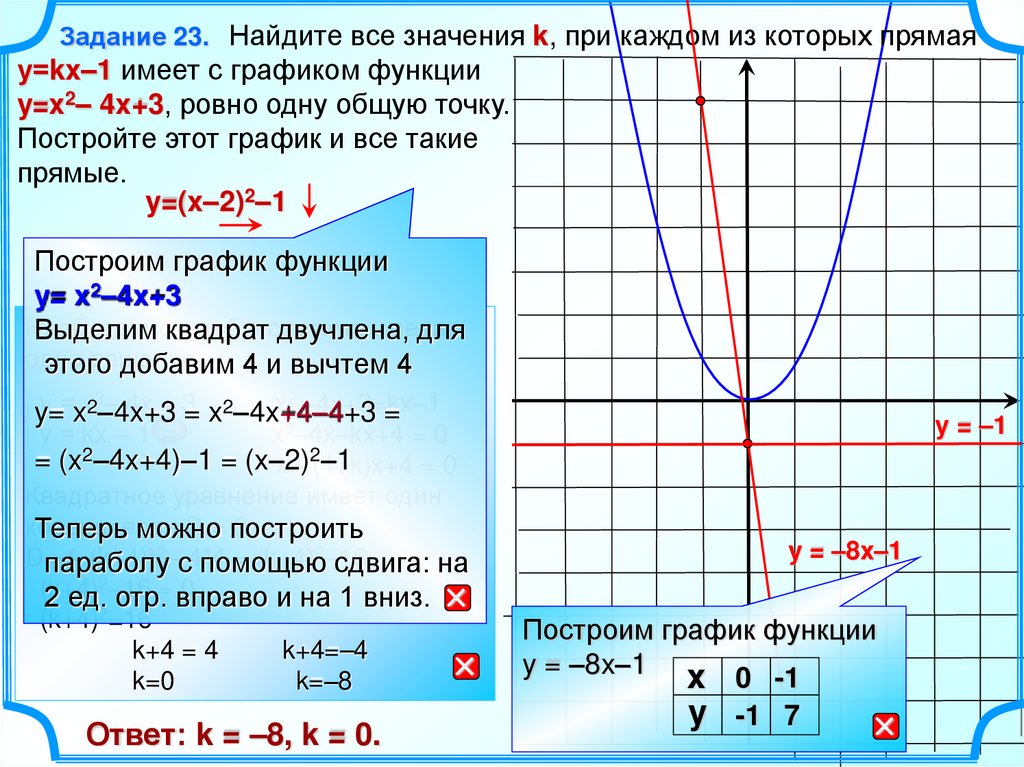
Задание 23. Найдите все значения k, при каждом из которых прямаяу=kx–1 имеет с графиком функции
y=x2– 4x+3, ровно одну общую точку.
Постройте этот график и все такие
прямые.
y=(x–2)2–1
Построим график функции
y= x2–4x+3
Необходимо,
чтобы система
имела
Выделим квадрат
двучлена,
для
одно
решение.
этого
добавим 4 и вычтем 4
у =xх2–4x+3
– 4x + 3= x2–4x+4–4+3
х –4x+3=kx–1
y=
=
2
2
2
х –4x–kx+4 = 0
2–1
= (x2–4x+4)–1 = (x–2)
х2–(4+k)x+4
=0
Квадратное уравнение имеет один
корень,
D = построить
0.
Теперьесли
можно
Dпараболу
=(–(k+4))2–с4*4
= (k+4)2–16
помощью
сдвига: на
2
(k+4)
0
2 ед.2–16
отр.= вправо
и на 1 вниз.
(k+4) =16
k+4 = 4
k+4=–4
k=0
k=–8
y = –1
у = kx – 1 =
Ответ: k = –8, k = 0.
y = –8x–1
Построим график функции
y = –8x–1 x 0 -1
y -1 7
3.
Задание 23Постройте график функции
Найдем
координаты2
2 + 4)(x + 1)
(x + 4)(x + 1)
(x
y = проколотой точки.
=
= –1(x2 + 4) = –x2– 4
–1 то
– xу= –(–1)2–4 =–1(1
x= –1,
–5 + x)
и определите, при
(–1;каких
–5) значениях k x= –1
y = –4x
y = 4x
прямая y = kx имеет с графиком
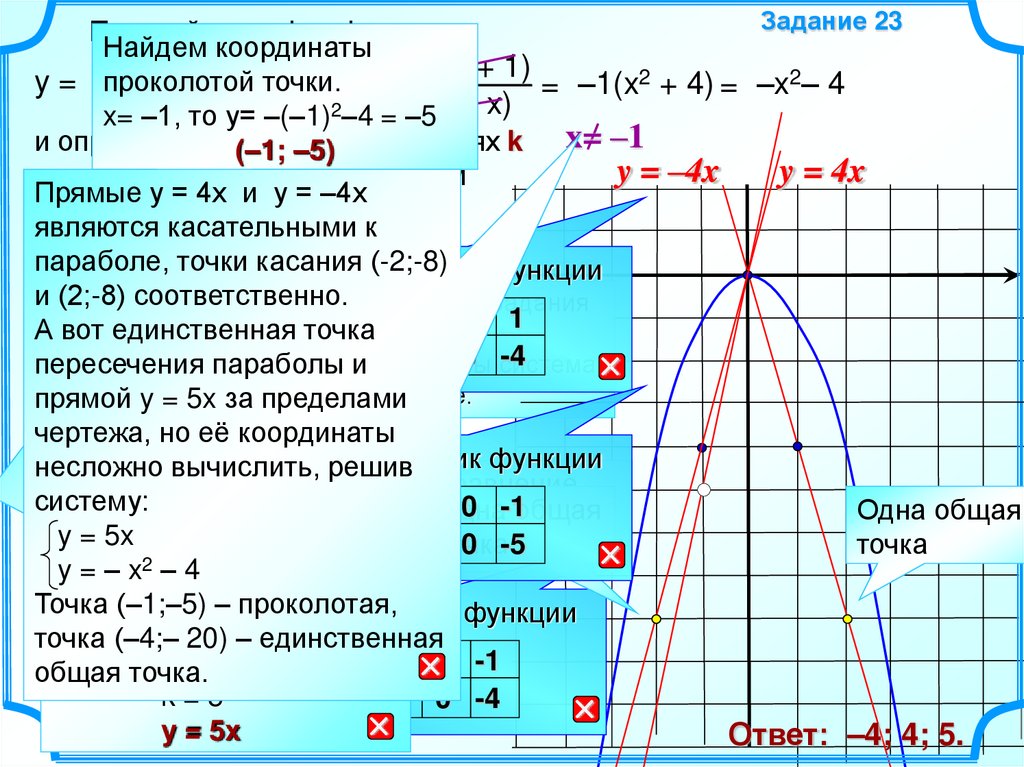
Прямые у = 4х и у = –4х
ровно одну общую точку.
являются касательными к
параболе,
касания (-2;-8)
y = –x2– 4точкиПостроим
график функции
иD(y):
(2;-8)xсоответственно.
Ответим
задания
= –1
y = – 4x на вопрос
0
1
x
А вот единственная
точка
аналитически.
yчтобы
0 система
-4
Необходимо,
параболы
и
yЕщё
kx
пересечения
одна общая
точка
1 решение.
y2 = 5x за имела
пределами
прямой
будет,
если
прямая y=kx,
y
x
4
чертежа,
но
её
пройдёт черезкоординаты
Построим график функции
несложно
2 вычислить, решив
проколотую
уравнение
kx
x 4 точку.
y Квадратное
= 5x
систему:
0 -1общая
Одна
Одна общая
Найдем коэффициент
имеет kодноx решение,
2y = 5x
0 -5
точка
для
этой
прямой.
если D = 0y точка
x y = kx
4
0
2
–x –4
2 у = kx
2
Точка
–Построим
проколотая,
D k(–1;–5)
4
1
4
k
16
график функции
–5
=
–1k
точка
– =единственная
2 (–4;– 20) y
4x
x 0 -1
k
16
0
;
k
=
–5
:
(–1)
общая точка.
k=5
y 0 -4
k y4= 5x
Ответ: –4; 4; 5.
4.
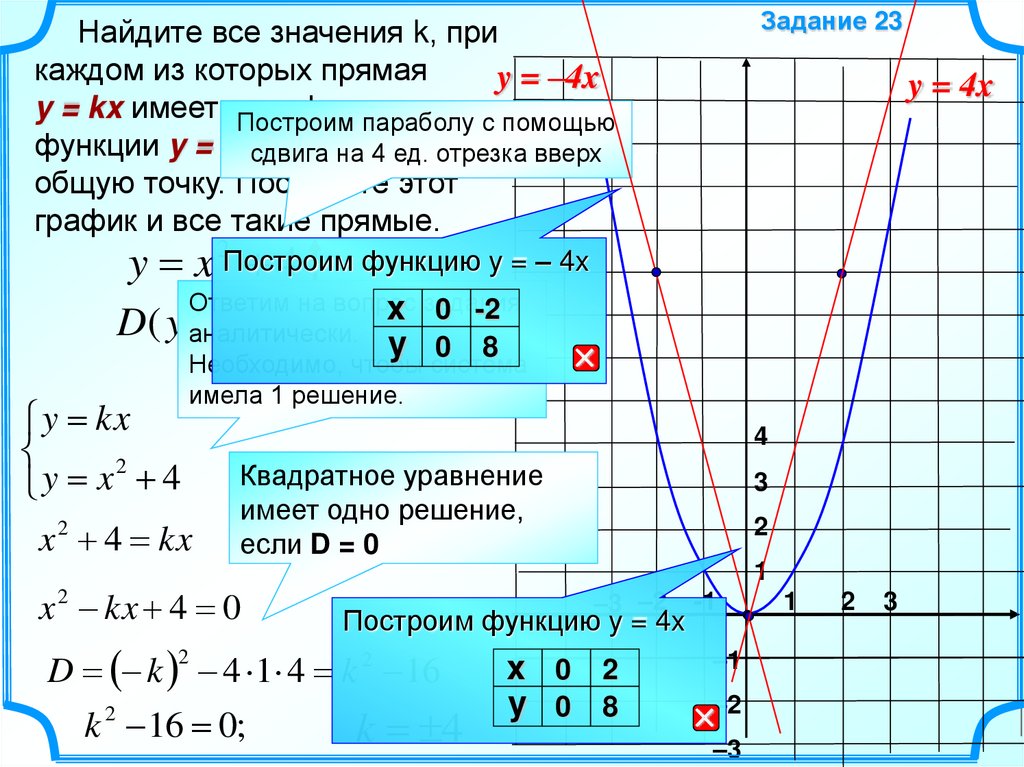
Задание 23Найдите все значения k, при
каждом из которых прямая
y = –4x
y = kx имеет сПостроим
графиком
параболу с помощью
2
функции y = x сдвига
+ 4 ровно
одну
на 4 ед.
отрезка вверх
общую точку. Постройте этот
график и все такие прямые.
y = 4x
y x 2Построим
4 функцию y = – 4x
Ответим на вопрос
задания
0 -2
x
D( y )аналитически.
: x R
y 0 8
Необходимо, чтобы система
имела 1 решение.
y kx
2
y
x
4
x 2 4 kx
4
Квадратное уравнение
имеет одно решение,
если D = 0
x 2 kx 4 0
2
–3 –2
Построим функцию y = 4x
2
k 16 0;
3
1
D k 4 1 4 k 2 16
2
k 4
x 0 2
y 0 8
-1
–1
–2
–3
1
2
3
5.
Найдите все значения k, прикаждом из которых прямая
y = kx имеет с графиком
y = –2x
функции y = – x2 – 1 ровно одну
общую точку. Постройте этот
график и все такие прямые.
y kx
2
y
x
1
kx x 2 1
аналитически.
0 -2
Необходимо,xчтобы
система
y 0 4
имела 1 решение.
Квадратное уравнение
Одна общая
имеет одно решение,
точка
если D = 0
D k 2 4 1 1 k 2 4
k 4 0;
k 2
y = 2x
Ответим на
вопрос задания
Построим
функцию
y = – 2x
x 2 kx 1 0
2
Задание 23
Построим функцию y = 2x
x 0 2
y 0 4
Одна общая
точка
6.
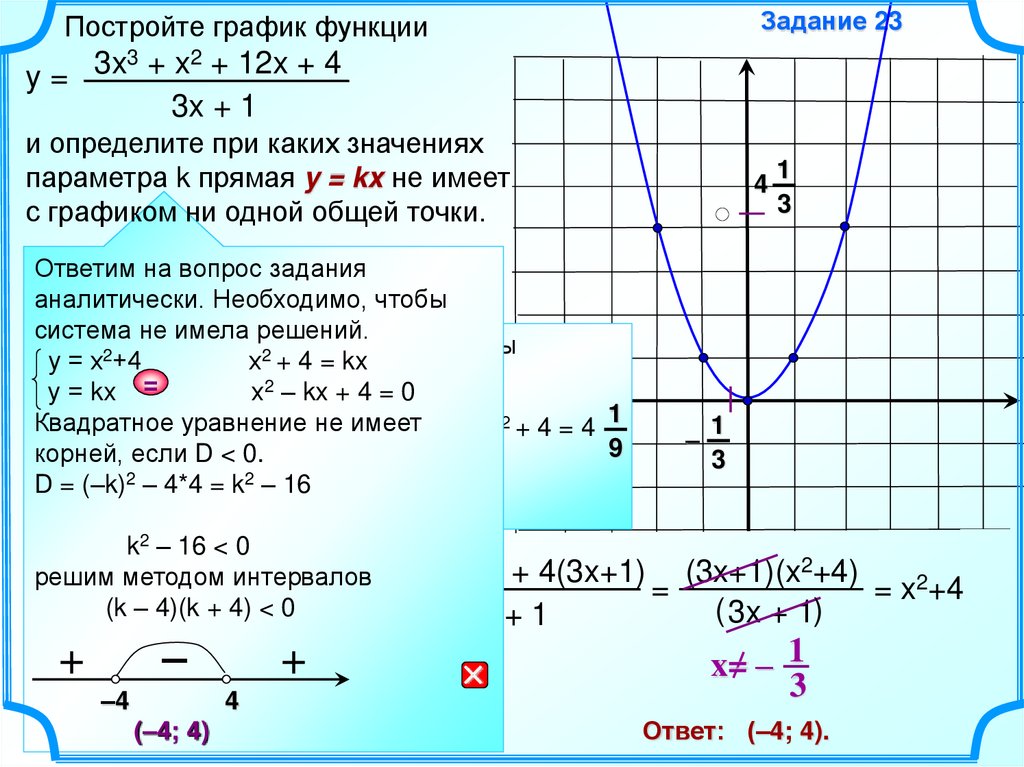
Задание 23Постройте график функции
3 + x2 + 12x + 4
3x
y=
3x + 1
и определите при каких значениях
параметра k прямая y = kx не имеет
с графиком ни одной общей точки.
4
1
3
Ответим на вопрос задания
аналитически. Необходимо, чтобы
система
не имела решений.
y = x2+4
Найдем координаты
у = х2+4
х2 + 4 = kx
точки.
= – 1 х2проколотой
D(y):
у = kx x=
– kx + 4 = 0
3
1
1
1
Квадратное уравнение
1
x = не
– имеет
, то у =(– )2 + 4 = 4
–
3
3
9
корней, если D < 0.
3
1
2
2
1
D = (–k) – 4*4 = k –(–
16 ; 4 )
9
3
k2 – 16 < 0
3x3методом
+ x2 + 12x
+4
x2(3x+1) + 4(3x+1) (3x+1)(x2+4)
решим
интервалов
=
=
у = (k – 4)(k + 4) < 0
( 3x + 1)
3x + 1
3x + 1
–
+
–4
+
4
(–4; 4)
x= – 1
3
Ответ: (–4; 4).
= x2+4
7.
Постройте график функции Задание 233
2
3x одна
+ x общая
+ 12x точка
+4
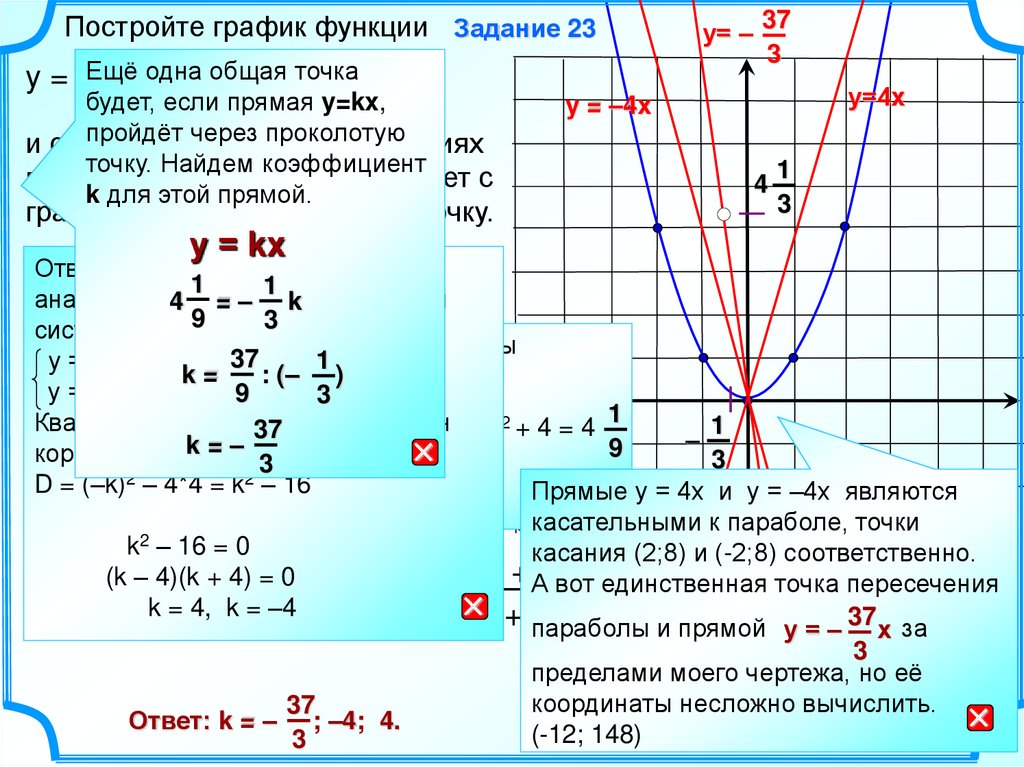
y = Ещё
будет, если
y=kx,
3x +прямая
1
пройдёт через
и определите
при проколотую
каких значениях
точку. Найдем коэффициент
параметра k прямая y = kx имеет с
k для этой прямой.
графиком ровно одну общую точку.
у = kx
у= –
37
3
у=4x
y = –4x
4
1
3
Ответим на вопрос задания
1
1
аналитически.
чтобы
4 Необходимо,
=– k
9
3
система
имела одно решение.
y = x2+4
Найдем координаты
37х2 + 4 1= kx
у = х2+4
=
: проколотой
(– )
точки.
= –k 1
D(y):
у = kx x=
9 х2 – kx3 + 4 = 0
3
1
1
1
Квадратное уравнение
1
– , тоодин
у =(– )2 + 4 = 4
37x = имеет
–
k
=
–
3
9
корень, если D = 0.3
3
3
1
2
2
1
D = (–k) – 4*4 = k –(–
16 ; 4 )
Прямые у = 4х и у = –4х являются
9
3
касательными к параболе, точки
2
k – 16 = 0
касания (2;8) и (-2;8) соответственно.
3
2
2
2+4)
3x(k –+ 4)(k
x ++ 12x
x (3x+1) + А4(3x+1)
(3x+1)(x
4) = 0+ 4
вот единственная
точка пересечения
=
=
= x2+4
у=
k3x
= 4,+ k1= –4
( 3x + 1)
3x + параболы
1
и прямой у = – 37 х за
1 3
x=
–
пределами моего чертежа, но её
3
координаты несложно вычислить.
37
Ответ: k = – ; –4; 4.
(-12;
148)
3
8.
y=(x2–3х+2)(x2+3x+2)
x2–4
Задание 23
=
(x – 2 )(х – 1)(x +2
– )(x +1
– )
=(x–1)(x+1) = x2–1
(x+2)(х–2)
y
х2–3x+2=0
х2+3x+2=0
х1+х2= 3
х1 х2= 2
х1+х2= –3
х1 х2= 2
х1= 2
х2= 1
х1=–2
х2=–1
х2–3x+2=(x–2)(x–1)
5
ГОТОВИМСЯ x
х2+3x+2=(x+2)(x+1)
К
ОГЭ
Постройте график функции
x
y
2
3х 2 x 2 3x 2
x2 4
и определите, при каких
значениях k построенный
график будет иметь одну
общую точку с прямой y = kx.
Используем формулу для
разложения квадратного трехчлена
на множители
ax2+bx+c=a(x-x1)(x-x2 )
y=x2–1
D(y): x= 2, х=–2.
9.
Задание 23Если x=–2, то y = (–2)2–1 = 3
Исключаем точку (–2; 3)
y=x2–1
D(y): x= 2, х=–2.
(2; 3)
(–2; 3)
Если x=2, то y=22–1 = 3
Исключаем точку (2; 3)
у = kx
у = kx
3 = 2k : 2
3 = –2k : (–2)
k = 1,5
k = –1,5
y
3
y = 1,5x
y = –1,5x
Постройте график функции
Одна общая точка будет,
x
y
2
3х 2 x 2 3x если
2 прямая y=kx, пройдёт–2
через проколотую точку.
2
x 4
Найдем коэффициент k для
и определите, при каких
этой прямой.
значениях k построенный
график будет иметь одну
общую точку с прямой y = kx.
Ответ: –1,5; 1,5.
y=1,5x
1
2
–1
y= –1,5x
x



 mathematics
mathematics








