Функции и их графики

1.

МБОУ СОШ №5 – «Школа здоровья и развития» г. Радужный
Учитель математики: Семёнова Елена Юрьевна

2.

x 2
1. Постройте график функции y 1 2
x 2x
и определите, при каких значениях т прямая у = т
не имеет с графиком ни одной общей точки.
Решение.
x 2
y 1 2
x 2x
x 2
x 2
1
1 2
1
1
x 2x
x x 2
x
при условии х 0 и х 2 0
D y ; 2 2; 0 0; .
х 0 и х 2.

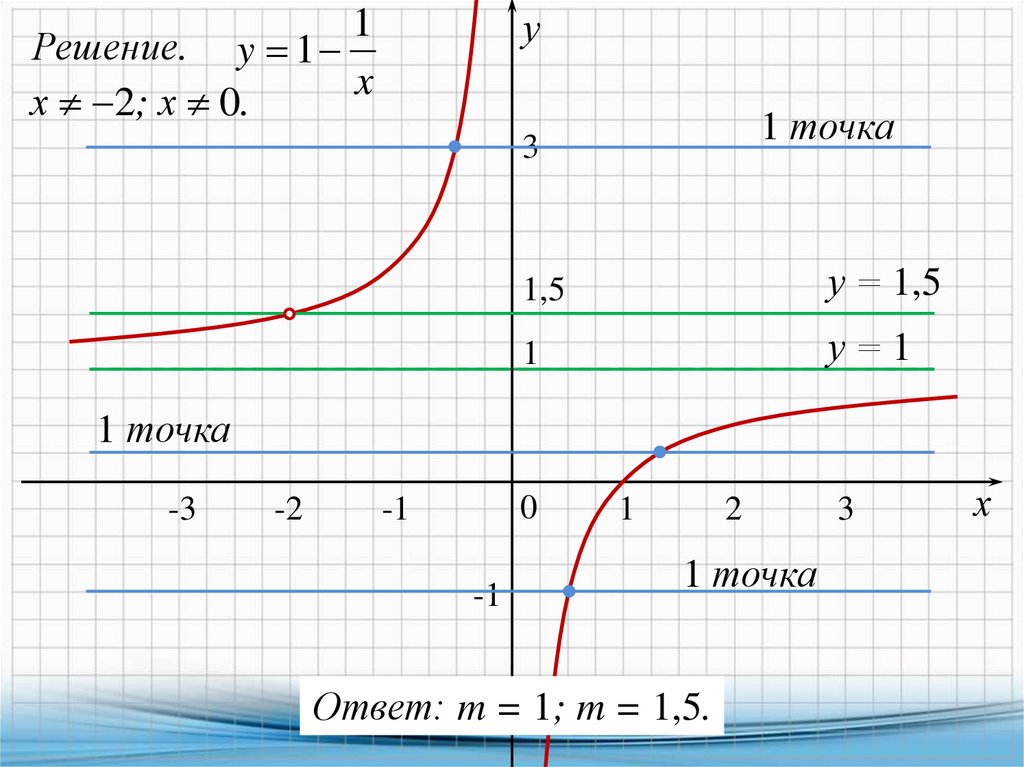
3.

у
1
Решение. y 1
x
х 2; х 0.
1 точка
3
1,5
у = 1,5
1
у=1
1 точка
-3
-2
0
-1
-1
1
2
1 точка
Ответ: m = 1; m = 1,5.
3
х

4.

x x
2. Постройте график функции y 1
x x2
и определите, при каких значениях т прямая у = т
имеет с графиком две общие точки.
4
3
Решение.
x 4 x3
y 1
2
x x
4
3
3
x x
x x 1
2
1
1
1
x
x x2
x x 1
при условии х 0 и х 1 0
D y ; 1 1; 0 0; .
х 0 и х 1.

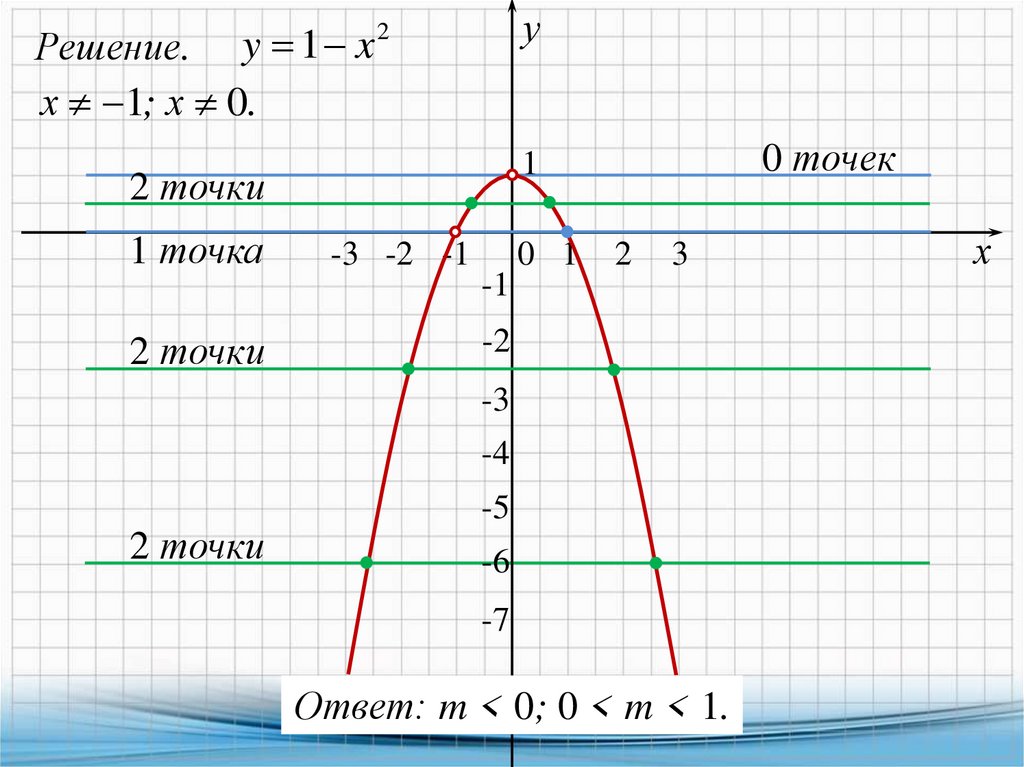
5.

у
2
Решение. y 1 x
х 1; х 0.
2 точки
1 точка
2 точки
0 точек
1
-3 -2 -1
-1
0 1
2
3
-2
-3
-4
2 точки
-5
-6
-7
Ответ: m < 0; 0 < m < 1.
х

6.

3. Постройте график функции
x 5 x 2 5 x 4
y
x 4
и определите, при каких значениях т прямая у = т
имеет с графиком ровно одну общую точку.
Решение.
x 5 x 2 5 x 4
y
x 4
x 5 x 2 5x 4 x 5 x 4 x 1 x 5 x 1
x 4
x 4
2
2
x 6x 5 x 3 4
при условии х 4 0 х 4.
D y ; 4 4; .

7.

Решение.
y x 3 4
2
у
х 4.
2 точки
4
3
2
2 точки
1
-6 -5 -4 -3 -2 -1
0 1
2
-1
-2
у(-4) = -3
у(-3) = -4
х
3
-3
-4
-5
Ответ: m = ‒ 4; m = ‒ 3.
2 точки
1 точка
1 точка

8.

4. Постройте график функции y x 2 x 2
Какое наибольшее число общих точек график данной функции
может иметь с прямой, параллельной оси абсцисс?
Решение.
y x2 x 2
y1 x 2 x 2
2
b 1
1
1 1
xв
; yв 2 2 .
2a 2
4
2 2
x
y
0
-2
1
-2
-1
0
2
0
3
4
-2
4

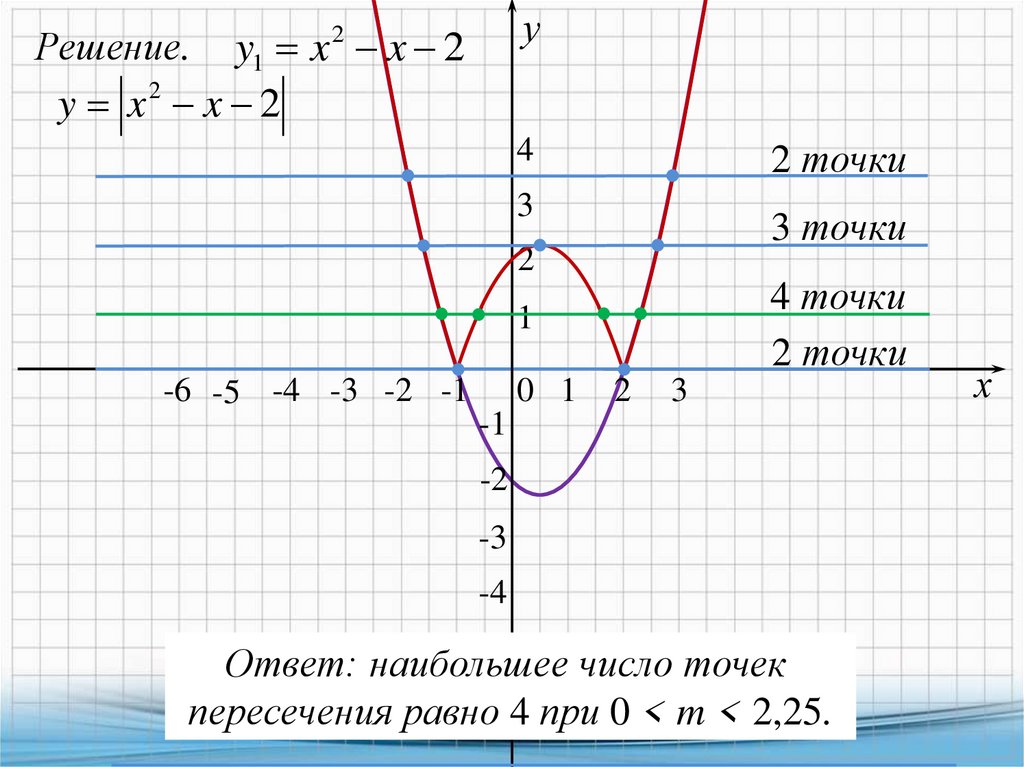
9.

у
Решение. y1 x 2 x 2
y x2 x 2
4
2 точки
3
3 точки
2
4 точки
2 точки
1
-6 -5 -4 -3 -2 -1
0 1
2
3
-1
-2
-3
-4
-5
Ответ: наибольшее
число точек
пересечения равно 4 при 0 < m < 2,25.
х

10.

5. Постройте график функции y x 2 6 x 8
Какое наибольшее число общих точек график данной функции
может иметь с прямой, параллельной оси абсцисс?
Решение.
2
y x 6 x 8
y x 6 x 8, т.к . x x
2
2
y1 x 2 6 х 8
b
xв
3; yв 32 6 3 8 1.
2a
x
y
0
8
6
8
1
3
5
3
2
0
4
0
2

11.

у
Решение. y1 x 2 6 х 8
y x 6 x 8
2
2 точки
8
3 точки
4 точки
4
3
4 точки
2
1
0 1
-6 -5 -4 -3 -2 -1
-1
2
3
4
5
6
7
2 точки
Ответ: наибольшее
число точек
-2
пересечения равно 4 при – 1 < m < 8.
х

12.

x
y
x 6 x2 4x 5
6. Постройте график функции
2
x 2x 3
и определите, при каких значениях т прямая у = т
имеет с графиком ровно одну общую точку.
Решение.
2
2
x x 6 x 4x 5
y
x2 2x 3
2
2
x x 6 x 4 x 5 x 3 x 2 x 1 x 5
2
x 1 x 3
x 2x 3
2
2
x 2 x 5 x 3x 10 х 1,5 12,25.
при условии х 1 0, х 3 0 х 1 и х 3.
D y ; 1 1; 3 3; .
2

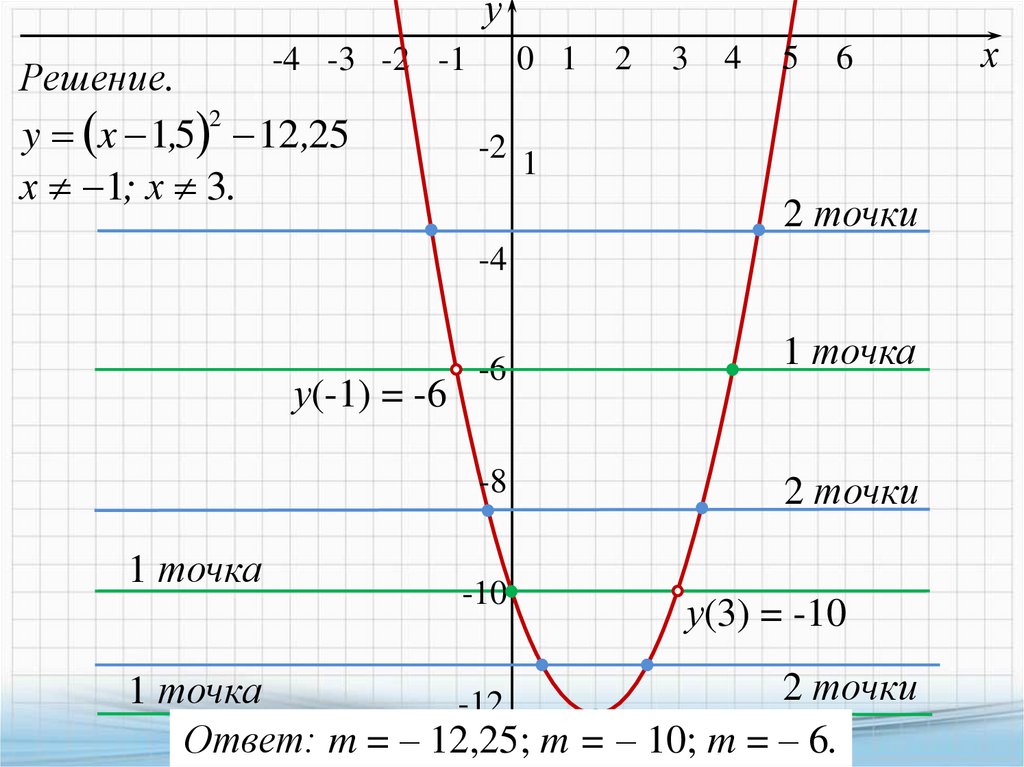
13.

у
0 1
-4 -3 -2 -1
Решение.
2
y x 1,5 12,25
х 1; х 3.
2
3
4
5
6
-2 1
2 точки
-4
у(-1) = -6
1 точка
-6
1 точка
-8
2 точки
-10
у(3) = -10
2 точки
1 точка
-12
Ответ: m = ‒ 12,25; m = ‒ 10; m = ‒ 6.
х

14.

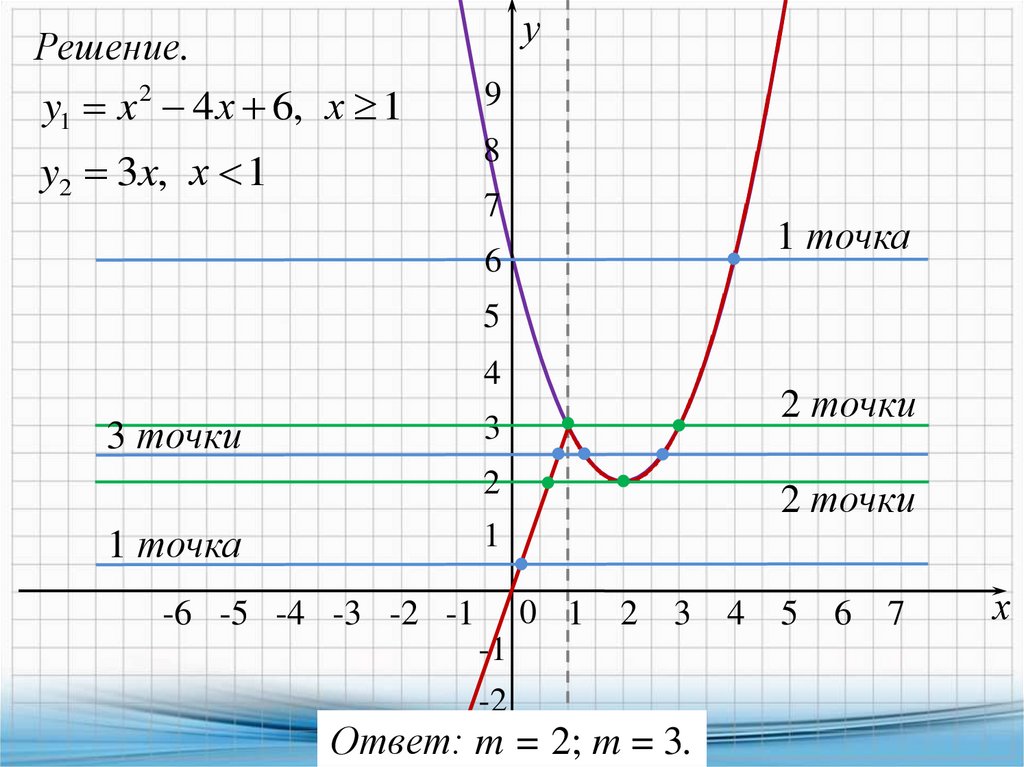
x 2 4 x 6, если х 1,
7. Постройте график функции y
3х, если х 1
и определите, при каких значениях т прямая у = т
имеет с графиком ровно две общие точки.
Решение.
x 2 4 x 6, если х 1,
y
3х, если х 1
y1 x 2 4 х 6
y2 3x
b
xв
2;
2a
yв 2 2 4 2 6 2.
x
y
0
0
-2
-6

15.

Решение.
2
y1 x 4 х 6, х 1
у
9
8
y2 3x, х 1
7
1 точка
6
5
4
3 точки
2 точки
3
2
1 точка
2 точки
1
0 1
-6 -5 -4 -3 -2 -1
2
3
-1
-2
Ответ: m = 2; m = 3.
4
5
6
7
х

16.

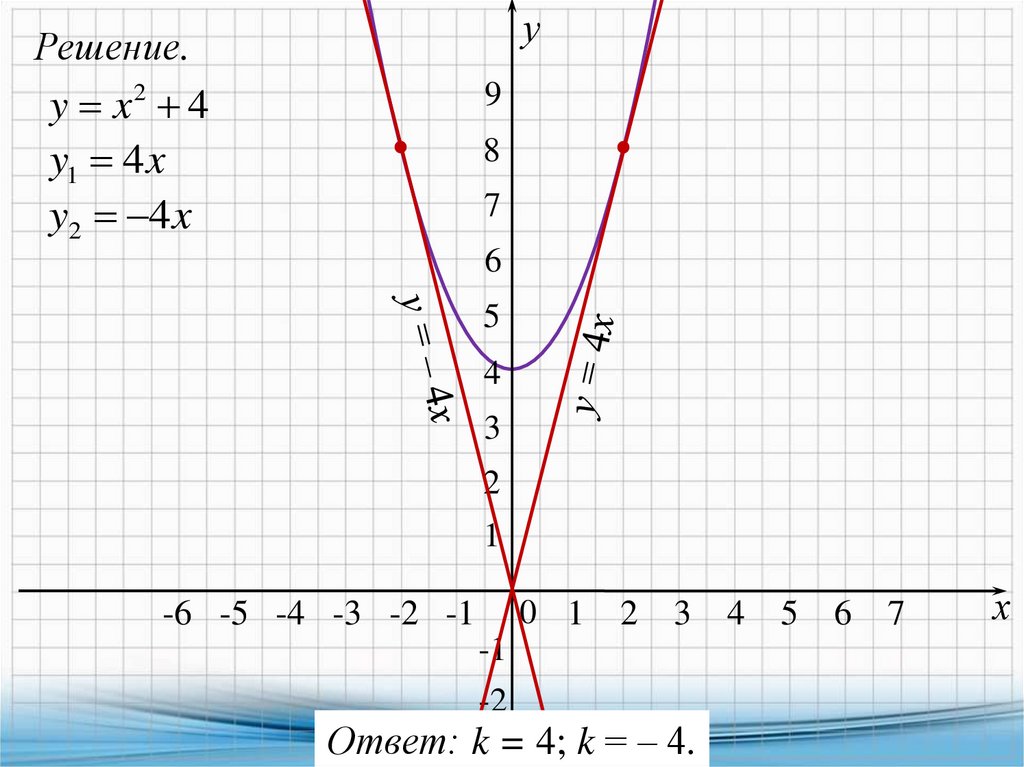
8. Найдите все значения k, при каждом из которых прямая y = kx
имеет с графиком функции y = x2 + 4 ровно одну общую точку.
Постройте этот график и все такие прямые.
Решение.
Другими словами, нужно найти все значения k, при каждом из
которых система имеет одно решение:
y x 2 4,
y kx;
kx x 2 4,
y kx;
kx x 2 4
x 2 kx 4 0
D k 2 16
1 корень D 0 k 2 16 0 k 4.

17.

у
Решение.
2
y x 4
y1 4 x
y2 4x
9
8
7
6
5
4
3
2
1
0 1
-6 -5 -4 -3 -2 -1
2
3
-1
-2
Ответ: k = 4; k = ‒ 4.
4
5
6
7
х

18.

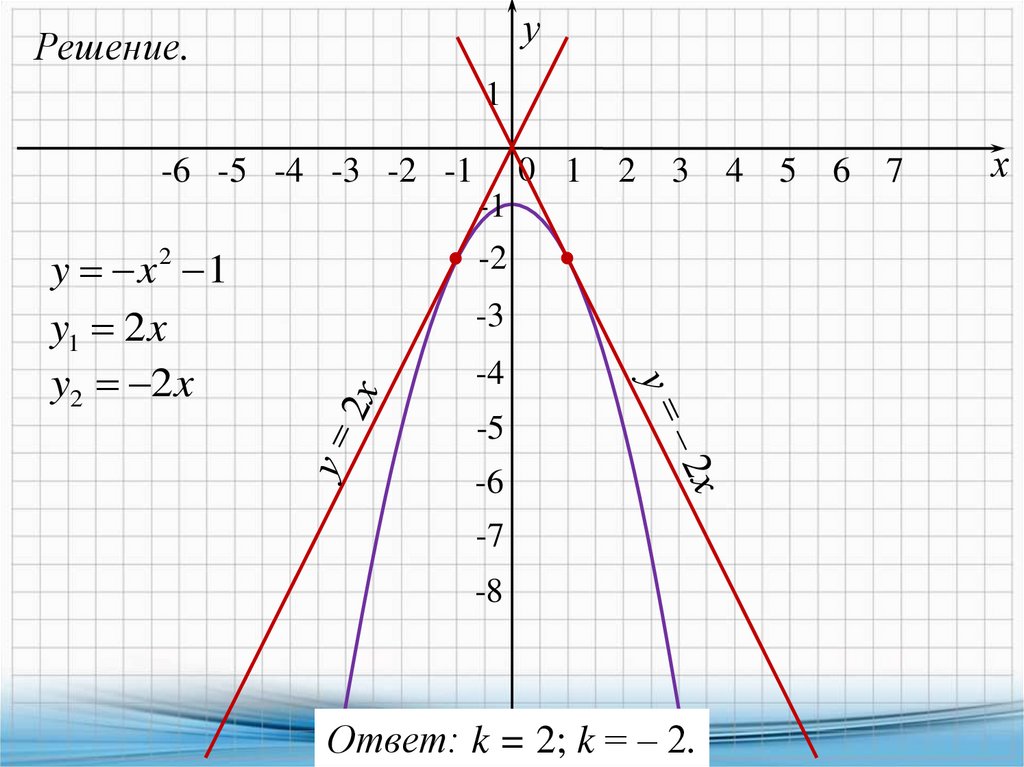
9. Найдите все значения k, при каждом из которых прямая y = kx
имеет с графиком функции y = ‒ x2 – 1 ровно одну общую точку.
Постройте этот график и все такие прямые.
Решение.
Другими словами, нужно найти все значения k, при каждом из
которых система имеет одно решение:
y x 2 1,
kx x 2 1,
y kx;
y kx;
kx x 2 1
x 2 kx 1 0
D k2 4
1 корень D 0 k 2 4 0 k 2.

19.

у
Решение.
1
0 1
-6 -5 -4 -3 -2 -1
2
3
-1
y x2 1
y1 2 x
y2 2x
-2
-3
-4
-5
-6
-7
-8
Ответ: k = 2; k = ‒ 2.
4
5
6
7
х

20.

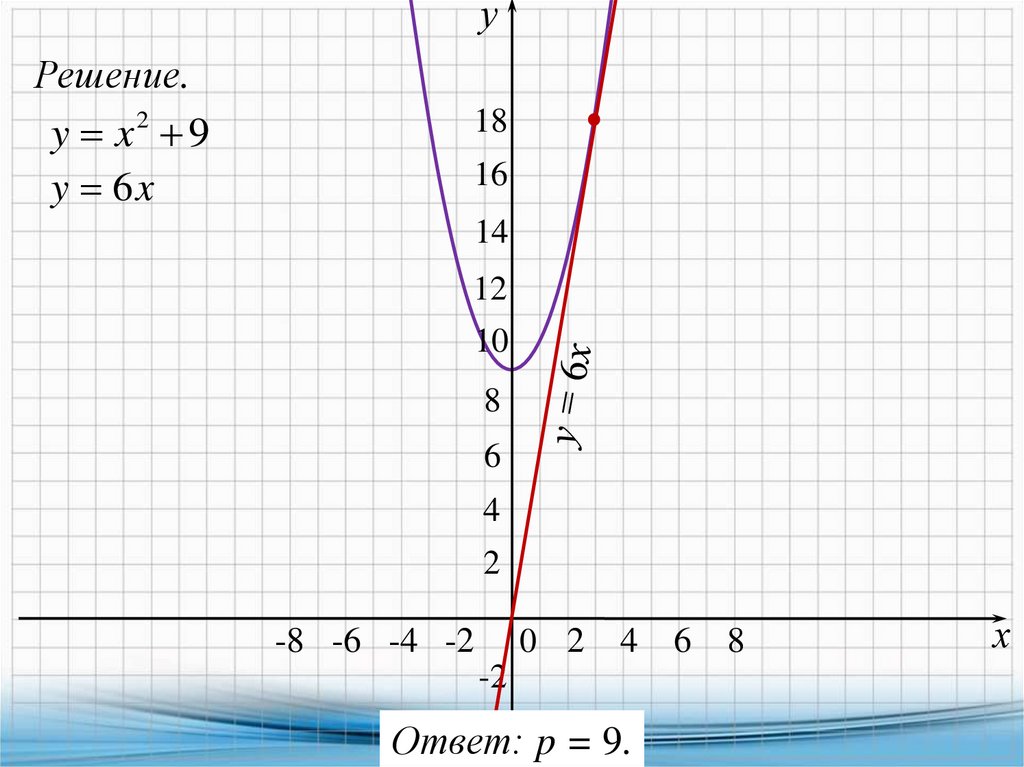
10. Найдите p и постройте график функции y = x2 + p если
известно, что прямая y = 6x имеет с этим графиком ровно одну
общую точку.
Решение.
Другими словами, нужно найти все значения p, при каждом из
которых система имеет одно решение:
y x2 p,
y 6 x;
6 x x 2 p ,
y 6 x;
6x x2 p
x2 6x p 0
D 36 4 p
1 корень D 0 36 4 p 0
p 9.

21.

у
Решение.
y x2 9
y 6x
18
16
14
12
10
8
6
4
2
-8 -6 -4 -2
0 2
4
-2
-4 p = 9.
Ответ:
6
8
х

22.

11. Постройте график функции
x
y
2
x x
x 1
и определите, при каких значениях т прямая у = т
не имеет с графиком ни одной общей точки.
Решение.
x2 x x
y
x 1
2
x
x 2 x x x x 1 x
, если х 0;
xx 2
x 1
x 1
х , если х 0.
при условии х 1 0
D y ; 1 1; .
х 1.

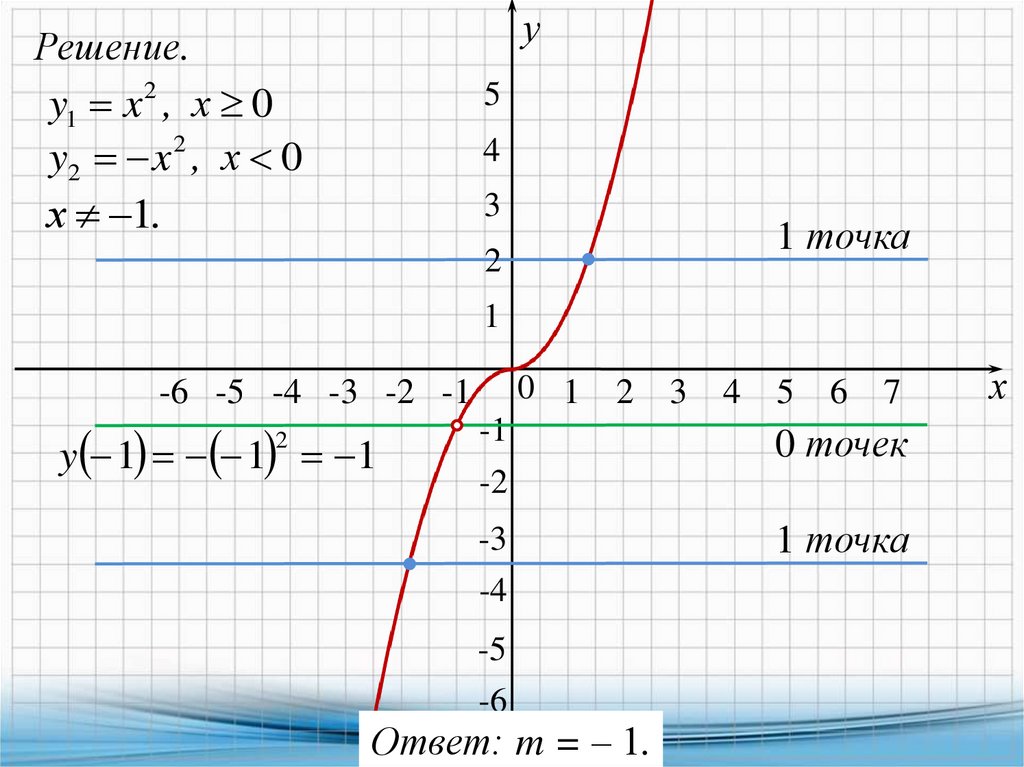
23.

у
Решение.
y1 x 2 , х 0
2
y2 x , х 0
5
4
х 1.
3
1 точка
2
1
0 1
-6 -5 -4 -3 -2 -1
y 1 1 1
2
2
3
4
5
6
7
-1
-2
0 точек
-3
-4
1 точка
-5
-6
Ответ: m = ‒ 1.
х

24.

x
y
2x x
12. Постройте график функции
x 2
и определите, при каких значениях т прямая у = т
не имеет с графиком ни одной общей точки.
Решение.
2
x 2x x
D y ; 2 2; .
y
x 2
2
2
x 2 x x x x 2 x
x , если х 0;
xx 2
x 2
x 2
х , если х 0.
при условии х 2 0 х 2.
2

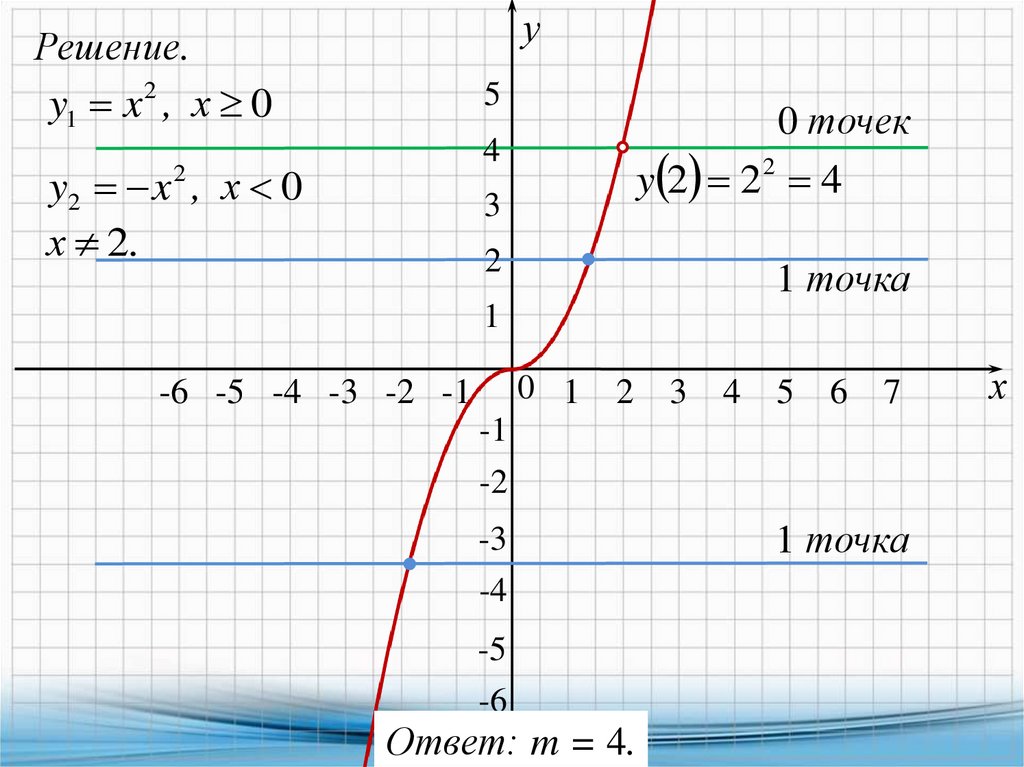
25.

у
Решение.
y1 x 2 , х 0
5
0 точек
2
y2 2 4
4
y2 x 2 , х 0
х 2.
3
2
1 точка
1
0 1
-6 -5 -4 -3 -2 -1
2
3
4
5
6
7
-1
-2
-3
-4
-5
-6
Ответ: m = 4.
1 точка
х

26.

x 2 4 x, если х 1,
13. Постройте график функции y
х 6, если х 1
и определите, при каких значениях т прямая у = т
имеет с графиком ровно две общие точки.
Решение.
x 2 4 x, если х 1,
y
х 6, если х 1
2
y2 x 6
y1 x 4 х
b
x
-2
xв
2;
2a
y
4
2
yв 2 4 2 4.
-6
0

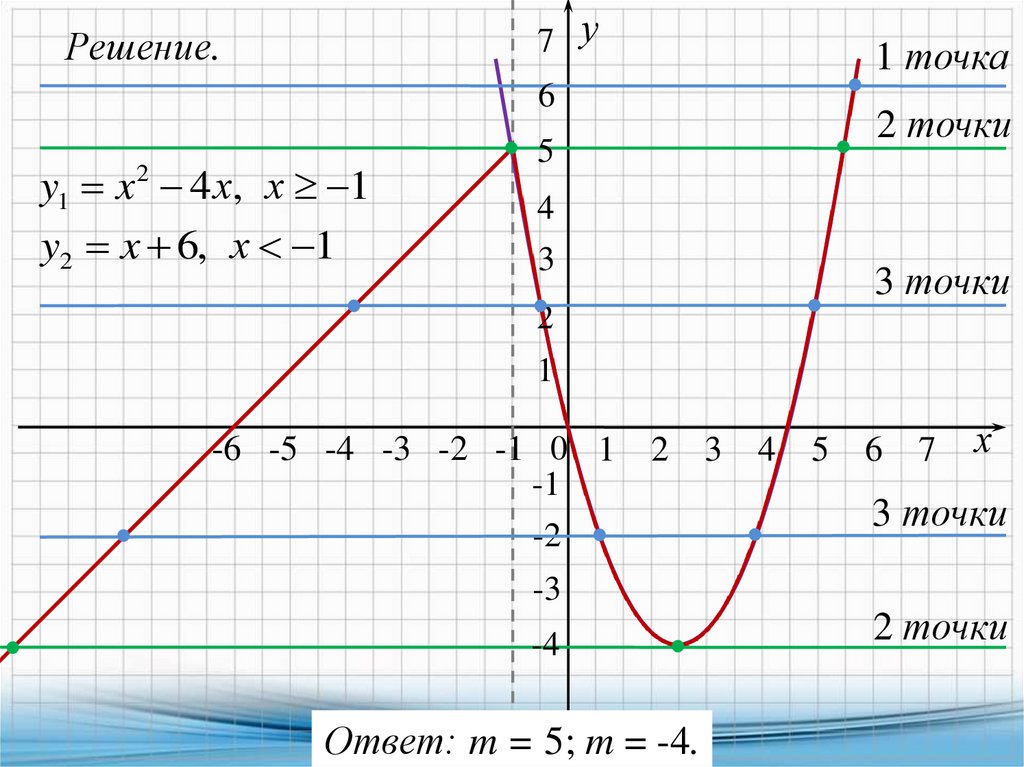
27.

7 у
Решение.
1 точка
6
y1 x 4 х, х 1
y2 x 6, х 1
2
2 точки
5
4
3
3 точки
2
1
-6 -5 -4 -3 -2 -1 0 1
-1
-2
2
-3
-4
Ответ: m = 5; m = -4.
3
4
5
6
7
х
3 точки
2 точки

28.

6 x x 2 , если х 1,
14. Постройте график функции y
х 8, если х 1
и определите, при каких значениях т прямая у = т
имеет с графиком ровно две общие точки.
Решение.
6 x x 2 , если х 1,
y
х 8, если х 1
2
y1 6 х x
b
6
xв
3;
2a
2
y в 6 3 3 2 9.
y2 x 8
x
y
-2
-6
-8
0

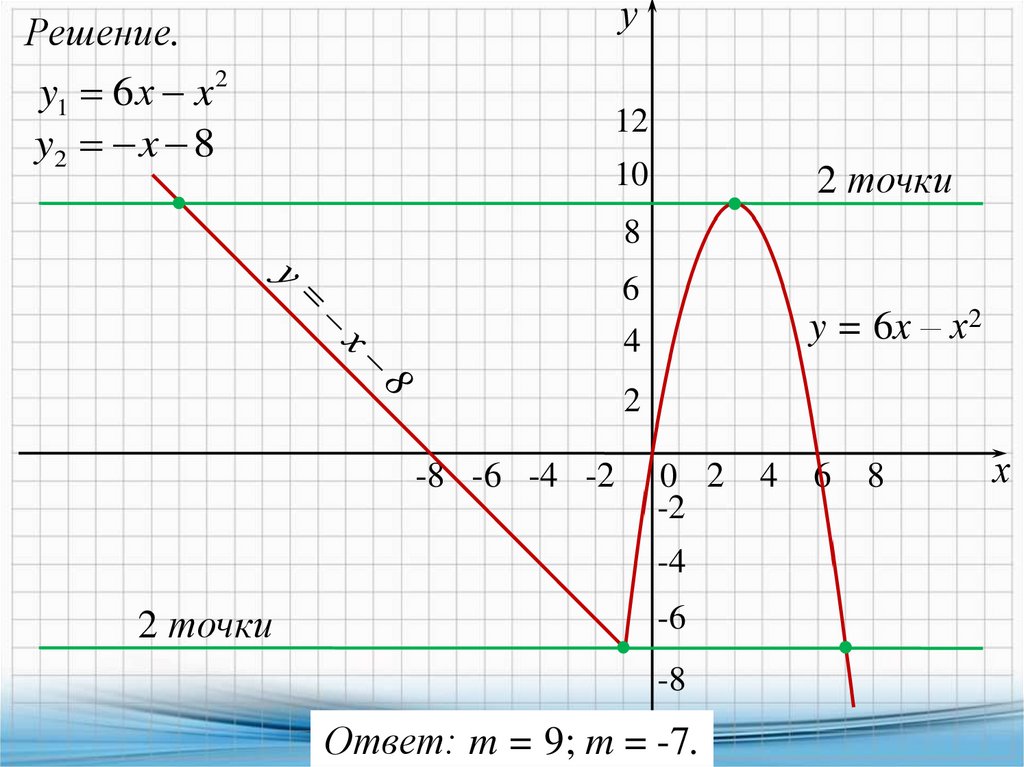
29.

Решение.
y1 6 х x 2
y2 x 8
у
12
2 точки
10
8
6
y = 6x – х2
4
2
-8 -6 -4 -2
0 2
-2
-4
2 точки
-6
-8
Ответ: m = 9; m -4
= -7.
4 6 8
х

30.

x
y
9 x 1
15. Постройте график функции
1 x
и определите, при каких значениях k прямая у = kx
имеет с графиком ровно одну общую точку.
Решение.
x 2 9 x 1
D y ; 1 1; .
y
1 x
x
2
9 x 1 x 9 x 1
x2 9
1 x
x 1
2
при условии х 1 0
х 1.
2

31.

Решение.
Другими словами, нужно найти все значения k, при каждом из
которых система имеет одно решение:
kx x 2 9,
y x 2 9,
y kx;
y kx;
kx x 2 9
x 2 kx 9 0
D k 2 36
1 корень D 0 k 2 36 0 k 6;
и при х 1, y 1 9 10 10 k 1 k 10.

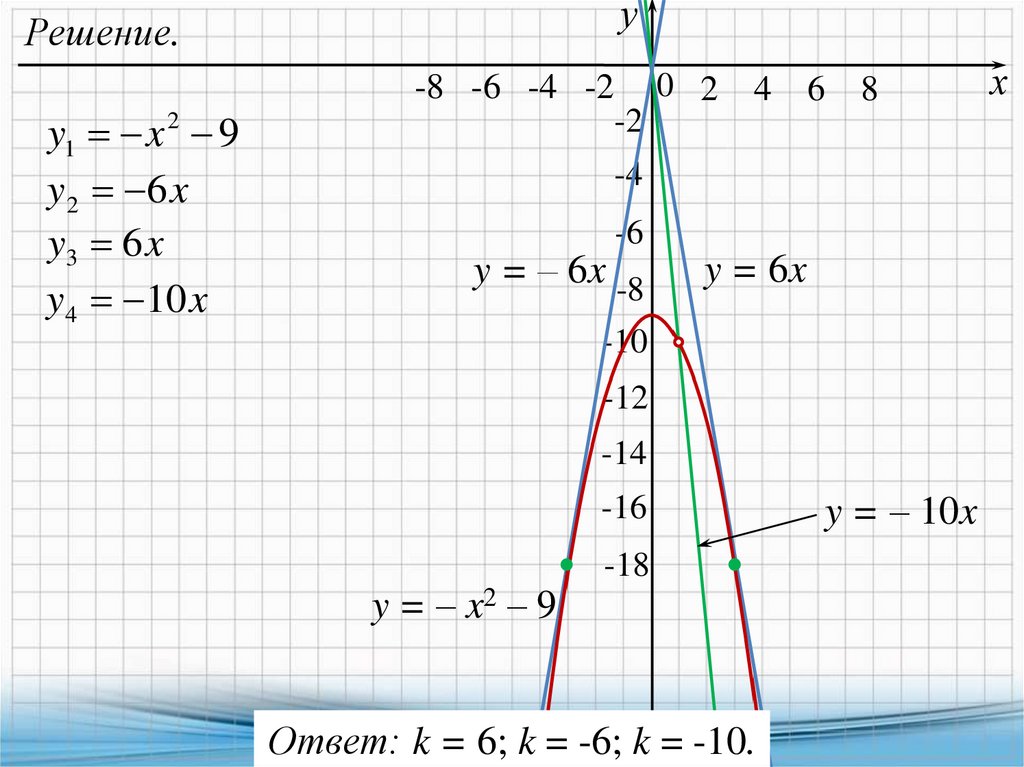
32.

у
Решение.
y1 x 2 9
y2 6 x
y3 6 x
y4 10 x
-8 -6 -4 -2 0 2
-2
-4
4
6
8
-6
y = – 6x -8
y = 6x
-10
-12
-14
-16
y = – x2 – 9
-18
Ответ: k = 6; k = -6; k = -10.
y = – 10x
х

33.

x 3, если х 1,
16.1. Постройте график функции y 1,5 x 4,5, если 3 х 4
1,5 х 7,5, если х 4
и определите, при каких значениях т прямая у = т
имеет с графиком ровно две общие точки.
Решение.
x 3, если х 1,
y 1,5 x 4,5, если 3 х 4
1,5 х 7,5, если х 4
y2 1,5 х 4,5
y1 х 3
x
y
-2
-5
-3
-6
x
y
3
0
4
-1,5
y3 1,5 x 7,5
x
y
5
0
7
3

34.

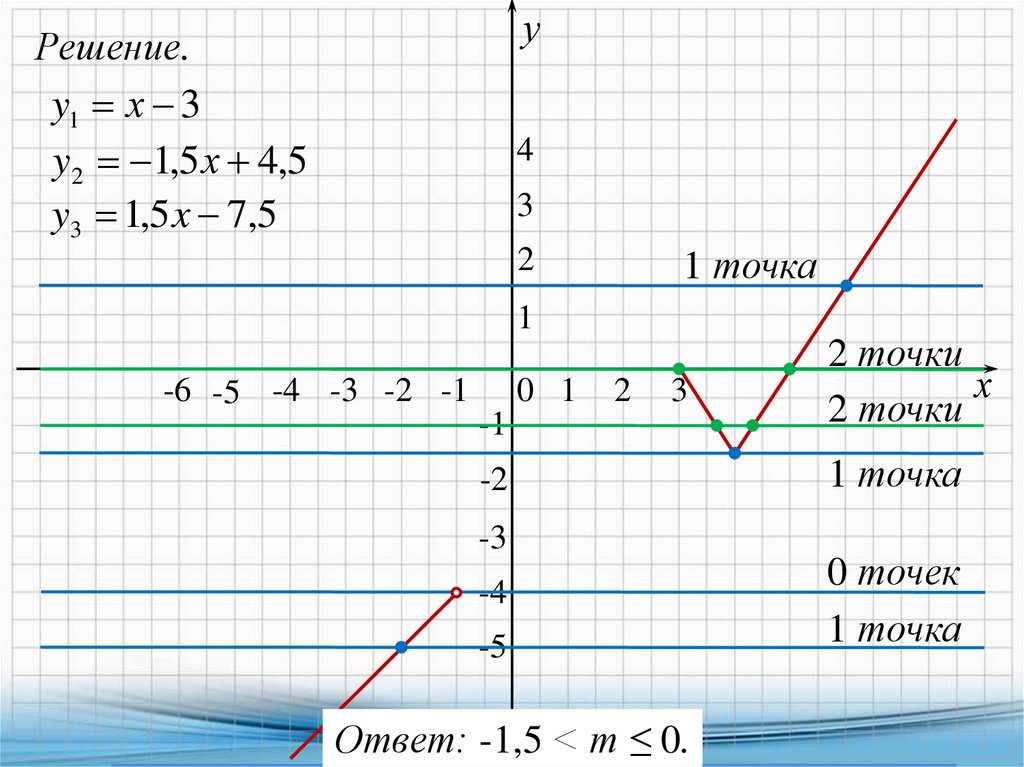
у
Решение.
y1 х 3
y2 1,5 х 4,5
y3 1,5 x 7,5
4
3
1 точка
2
1
-1
2 точки
х
2 точки
-2
1 точка
-6 -5 -4 -3 -2 -1
0 1
2
3
-3
-4
-5
Ответ: -1,5 < m ≤ 0.
0 точек
1 точка

35.

x 3, если х 3,
16.2. Постройте график функции y 1,5 x 4,5, если 3 х 4
1,5 х 7,5, если х 4
и определите, при каких значениях т прямая у = т
имеет с графиком ровно две общие точки.
Решение.
x 3, если х 3,
y 1,5 x 4,5, если 3 х 4
1,5 х 7,5, если х 4
y2 1,5 х 4,5
y1 х 3
x
y
2
-1
-3
-6
x
y
3
0
4
-1,5
y3 1,5 x 7,5
x
y
5
0
7
3

36.

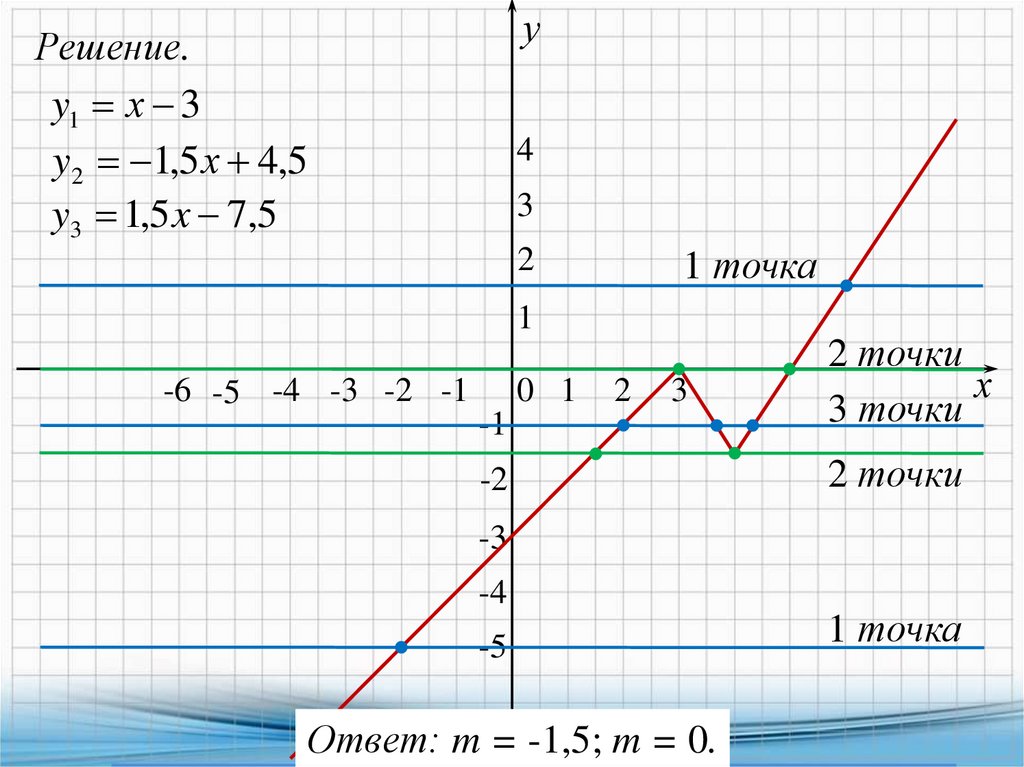
у
Решение.
y1 х 3
y2 1,5 х 4,5
y3 1,5 x 7,5
4
3
1 точка
2
1
-1
2 точки
х
3 точки
-2
2 точки
-6 -5 -4 -3 -2 -1
0 1
2
3
-3
-4
-5
Ответ: m = -1,5; m = 0.
1 точка

37.

http://www.mathgia.ru/or/gia12/Main.html - открытый банк
заданий ОГЭ по математике
Продолжение следует!