Презентация по теме _Функции и их свойства

1. «ФУНКЦИИ И ИХ СВОЙСТВА»

Урок-обобщение по теме:

2.

Слово «функция» в математике появилось
сравнительно недавно.
Впервые о функциях стал говорить
великий немецкий математик и философ
Г. В. Лейбниц в конце XVII века,
а первое определение
функции дал его ученик
И. Бернулли в 1718 году.
Впрочем, это было не то определение,
которым
мы
пользуемся
сегодня.
Определение функций было дано позднее –
в конце XIX века.

3. Что такое функция?

Функция – это такая зависимость переменной y
от переменной x, при которой каждому
значению переменной x соответствует
единственное значение переменной y.
Переменную x называют независимой
переменной или аргументом.
Переменную y называют зависимой
переменной. Переменная y является
функцией от переменной x.

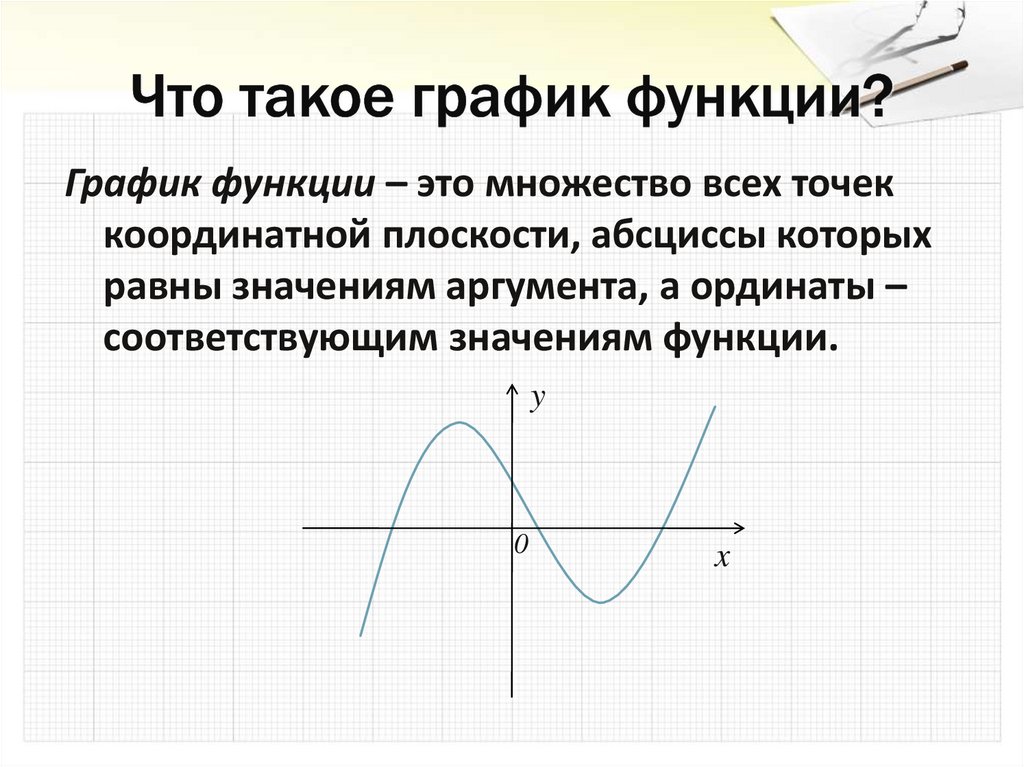
4. Что такое график функции?

График функции – это множество всех точек
координатной плоскости, абсциссы которых
равны значениям аргумента, а ординаты –
соответствующим значениям функции.
y
0
x

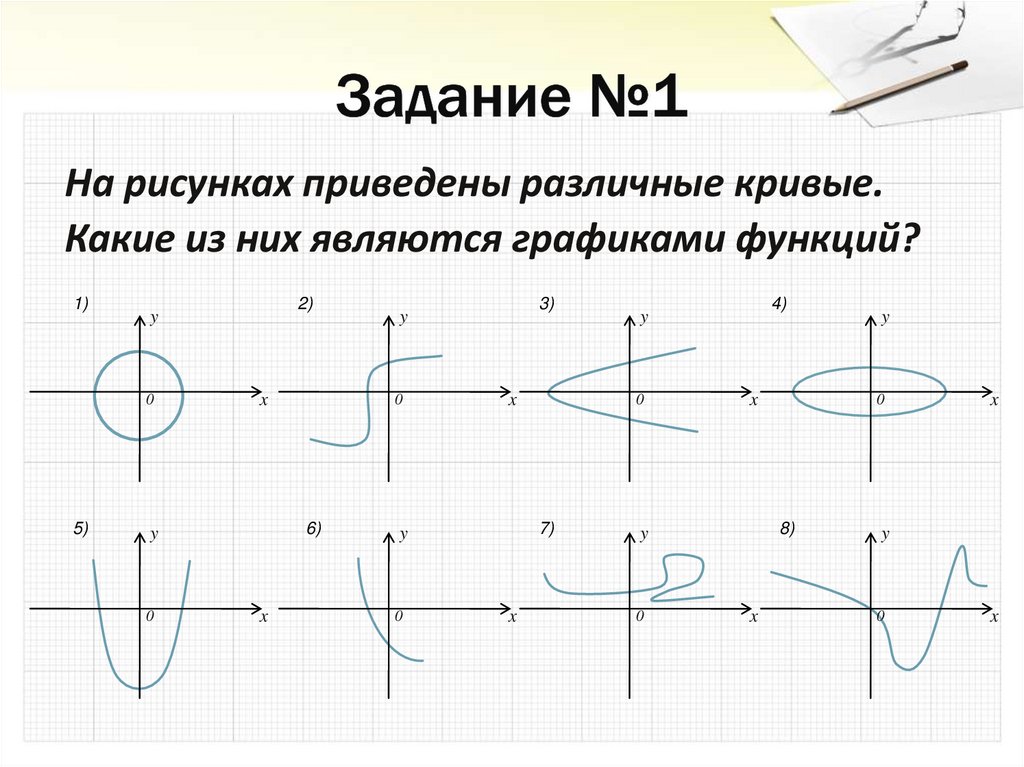
5. Задание №1

На рисунках приведены различные кривые.
Какие из них являются графиками функций?
1)
0
5)
2)
y
x
0
0
6)
y
x
3)
y
x
0
0
7)
y
x
4)
y
x
0
0
8)
y
x
y
x
y
0
x

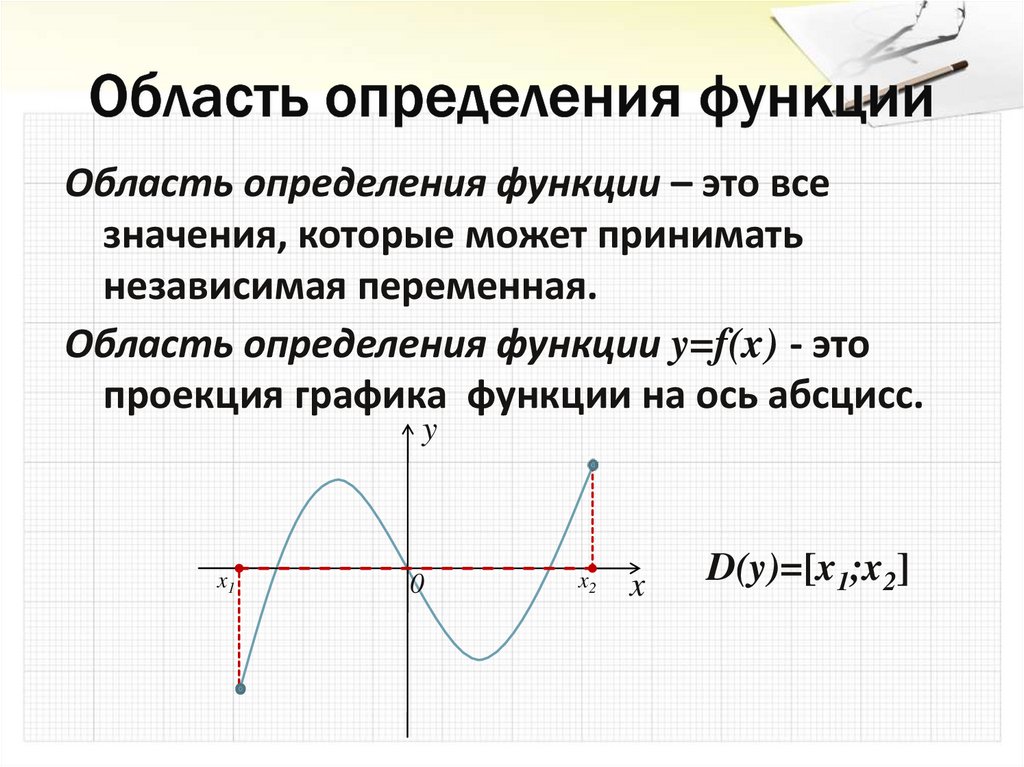
6. Область определения функции

– это все
значения, которые может принимать
независимая переменная.
Область определения функции y=f(x) - это
проекция графика функции на ось абсцисс.
y
x1
0
x2
x
D(y)=[x1;x2]

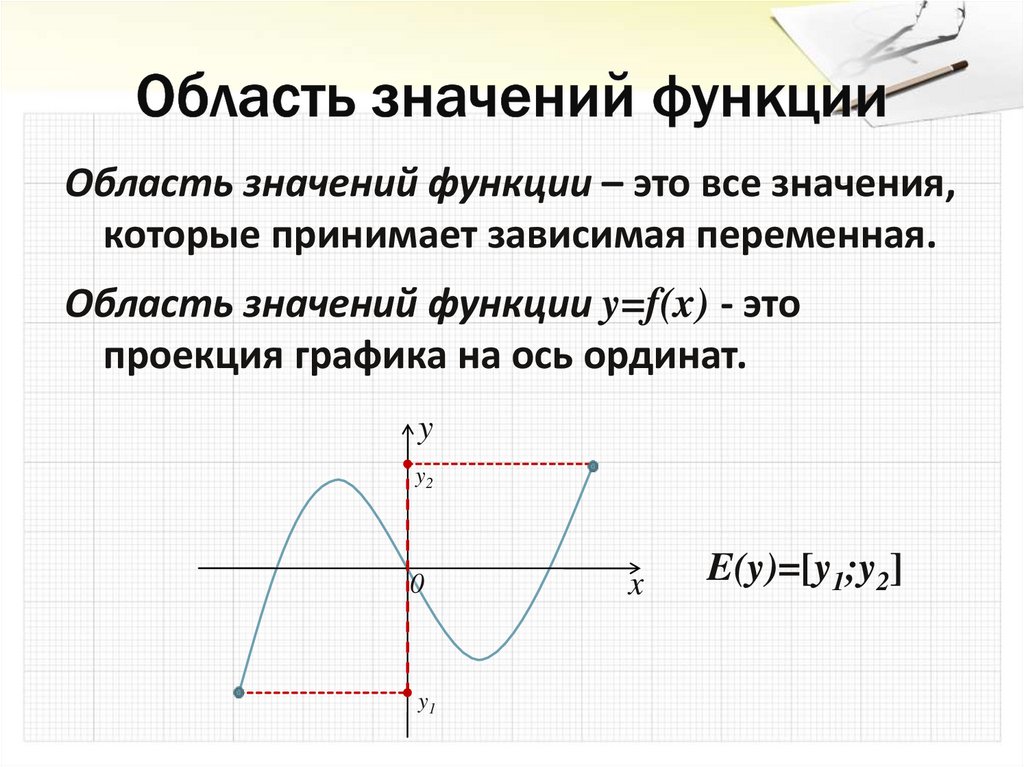
7. Область значений функции

– это все значения,
которые принимает зависимая переменная.
Область значений функции y=f(x) - это
проекция графика на ось ординат.
y
y2
0
y1
x
E(y)=[y1;y2]

8. Задание № 2.

1) Найти область определения функций:
а ) f x 29 3 x;
x ;
б ) f x 5 2 x ;
x ;2,5
2
в) f x
;
15 3 x
1
г ) f x
x 5.
2x
Ответы
x 5
x 5;

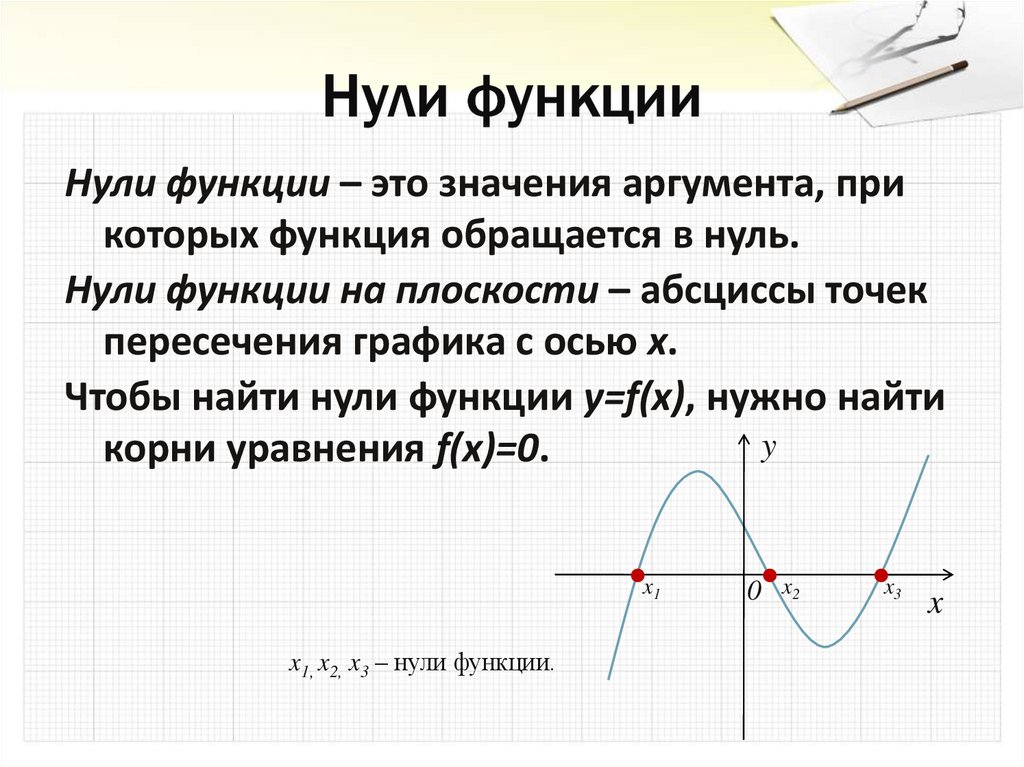
9. Нули функции

– это значения аргумента, при
которых функция обращается в нуль.
Нули функции на плоскости – абсциссы точек
пересечения графика с осью х.
Чтобы найти нули функции y=f(x), нужно найти
y
корни уравнения f(x)=0.
x1
x1, x2, x3 – нули функции.
0
x2
x3
x

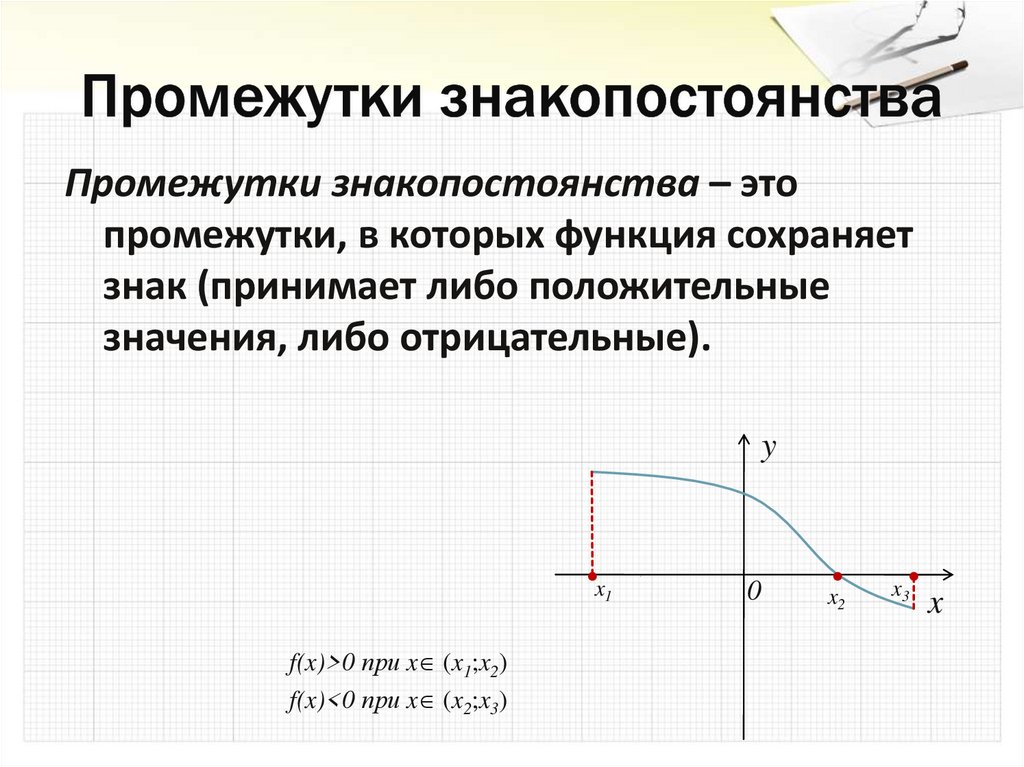
10. Промежутки знакопостоянства

– это
промежутки, в которых функция сохраняет
знак (принимает либо положительные
значения, либо отрицательные).
y
x1
f(x)>0 при x (x1;x2)
f(x)<0 при x (x2;x3)
0
x2
x3
x

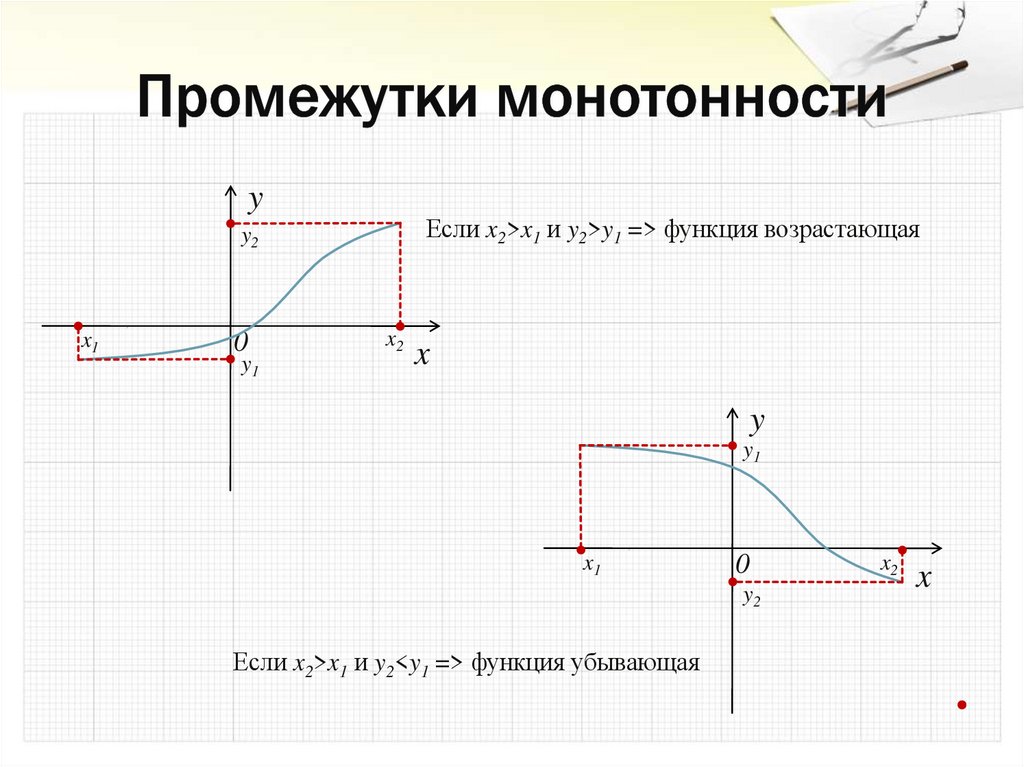
11. Промежутки монотонности

y
Если x2>x1 и y2>y1 => функция возрастающая
y2
x1
0
y1
x2
x
y
y1
x1
0
y2
Если x2>x1 и y2<y1 => функция убывающая
x2
x

12. Схема исследования функций

1) Найти область определения функции;
2) Найти область значений функции;
3) Найти нули функции;
4) Найти промежутки знакопостоянства
функции;
5) Найти промежутки возрастания и убывания
функции.

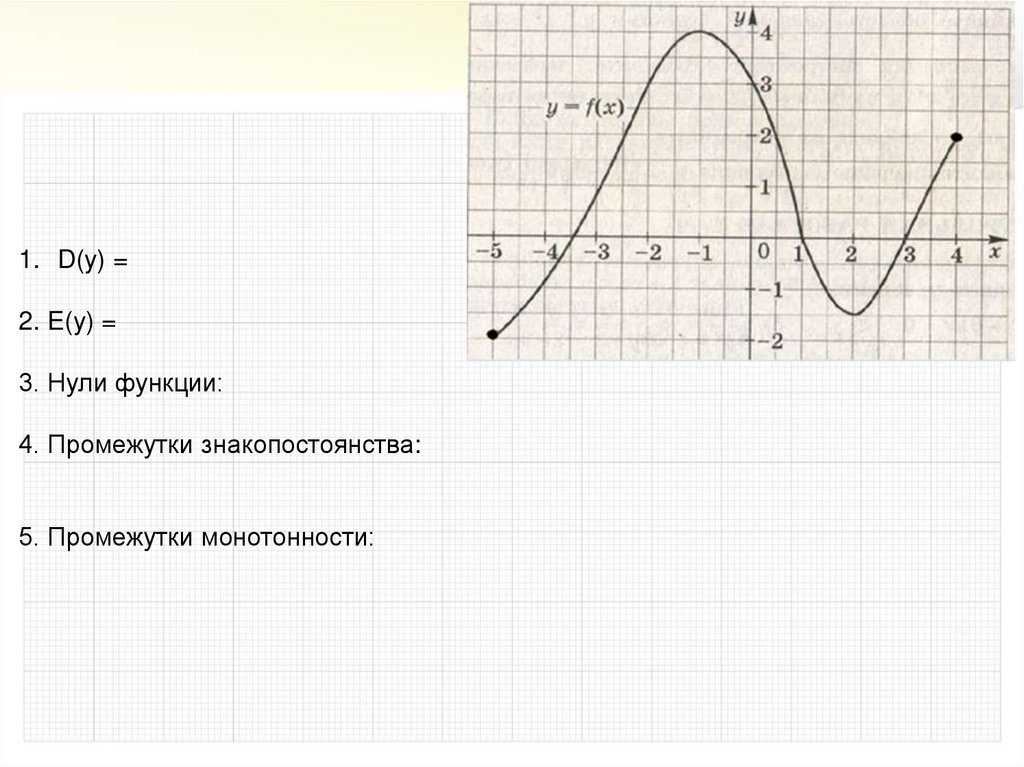
13.

1. D(y) =
2. E(y) =
3. Нули функции:
4. Промежутки знакопостоянства:
5. Промежутки монотонности:

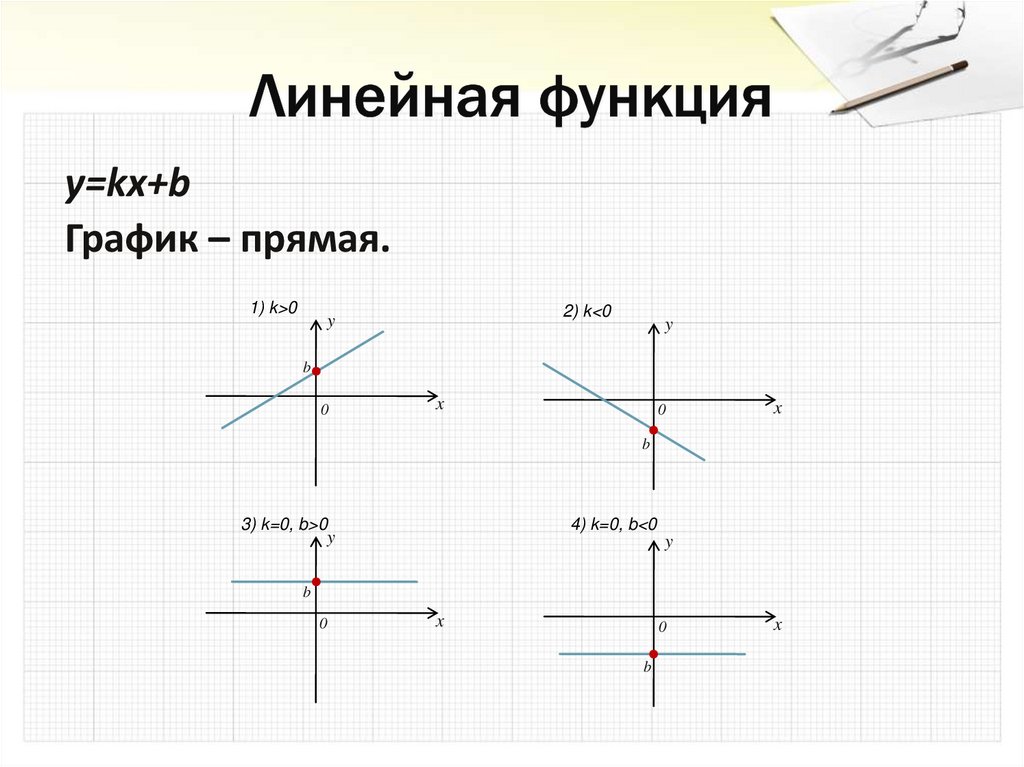
14. Линейная функция

y=kx+b
График – прямая.
1) k>0
2) k<0
y
y
b
0
x
0
x
b
3) k=0, b>0
4) k=0, b<0
y
y
b
0
x
0
b
x

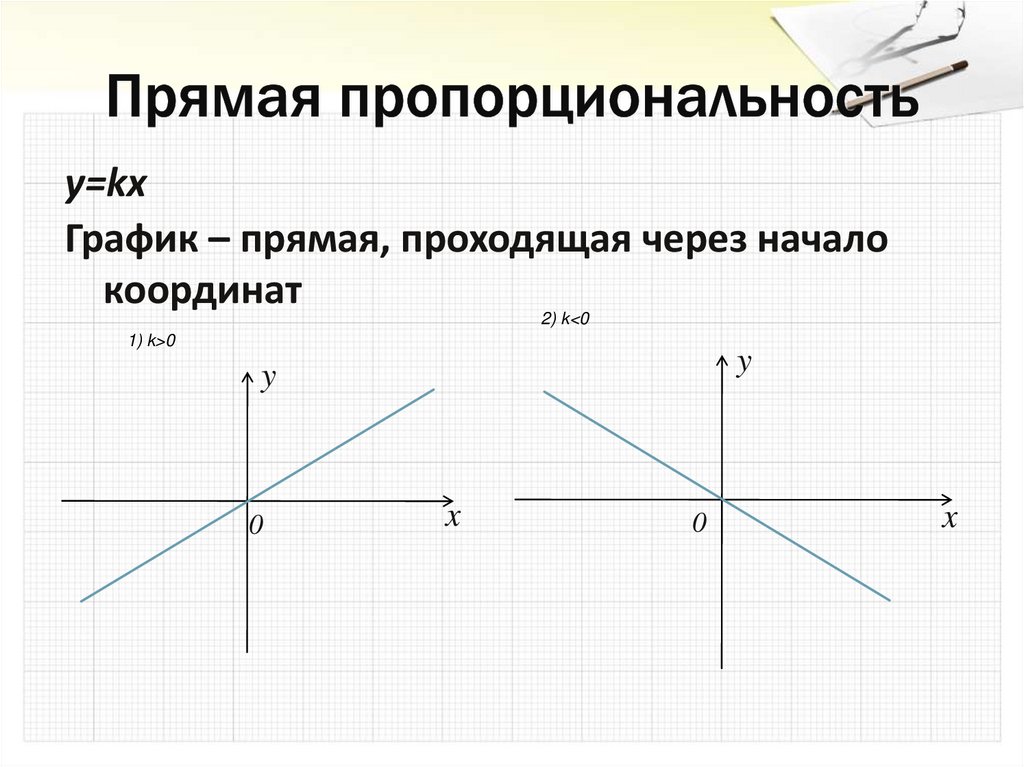
15. Прямая пропорциональность

y=kx
График – прямая, проходящая через начало
координат
2) k<0
1) k>0
y
y
0
x
0
x

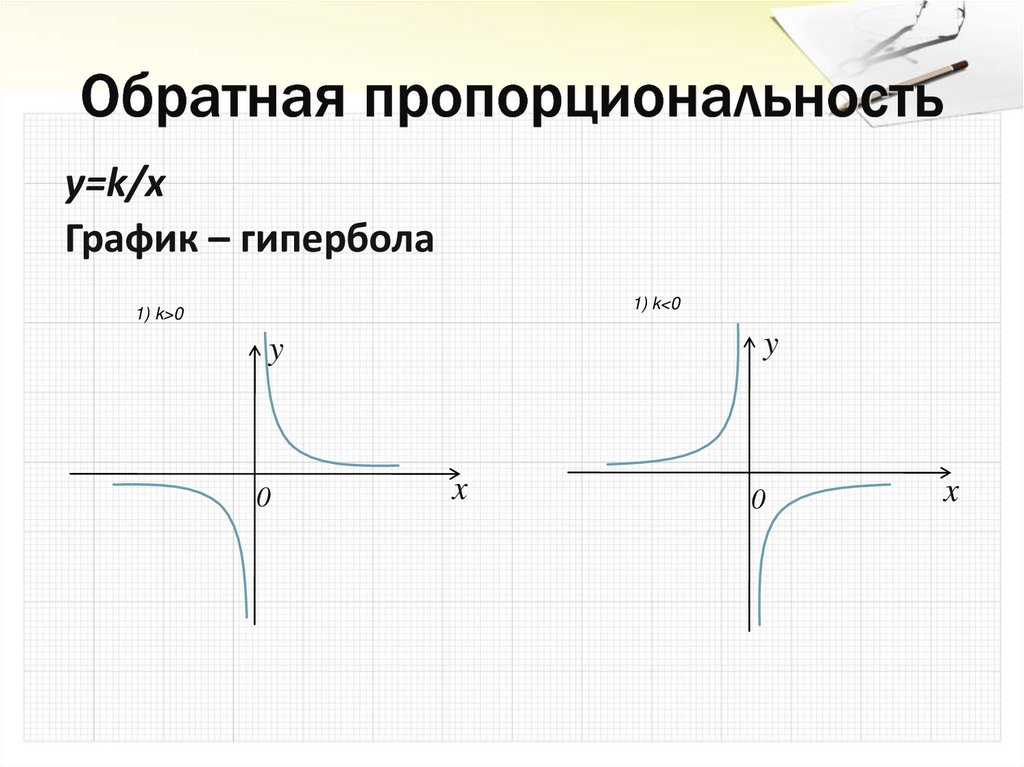
16. Обратная пропорциональность

y=k/x
График – гипербола
1) k<0
1) k>0
y
y
0
x
0
x

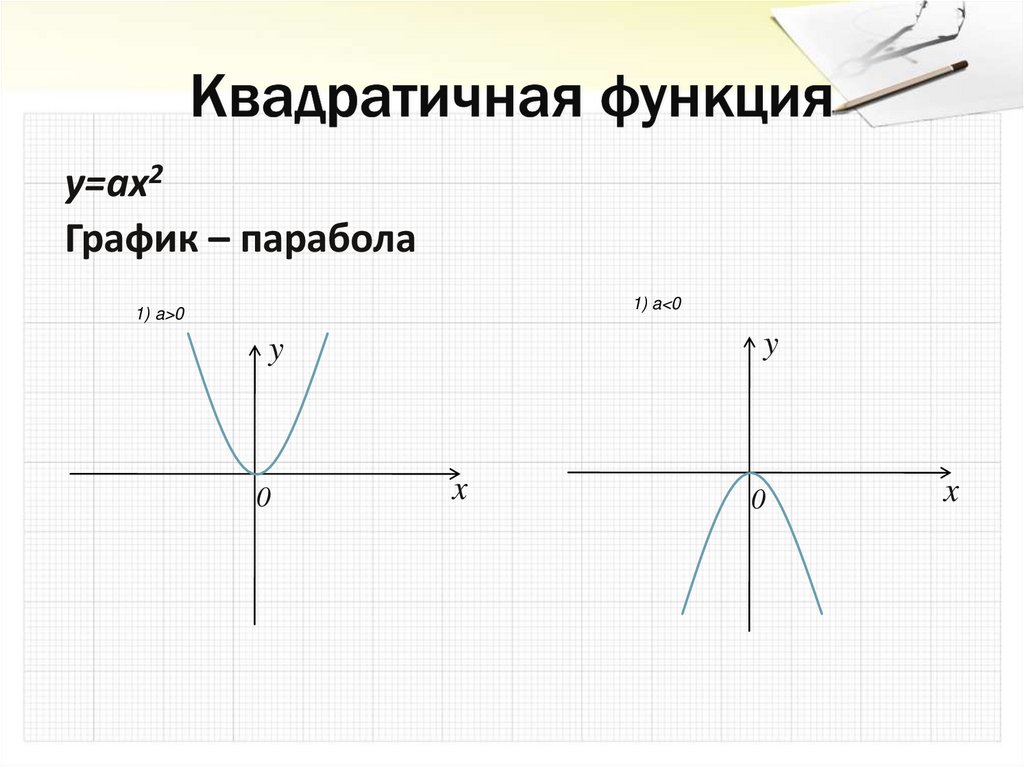
17. Квадратичная функция

y=ax2
График – парабола
1) a<0
1) a>0
y
y
0
x
0
x

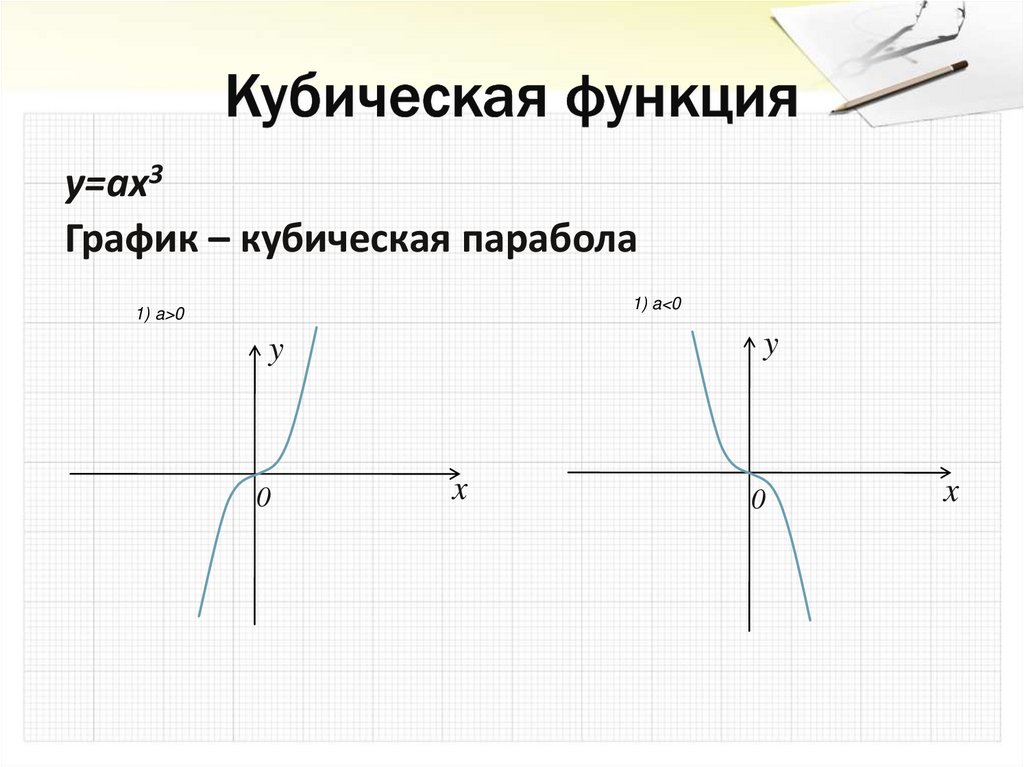
18. Кубическая функция

y=ax3
График – кубическая парабола
1) a<0
1) a>0
y
y
0
x
0
x

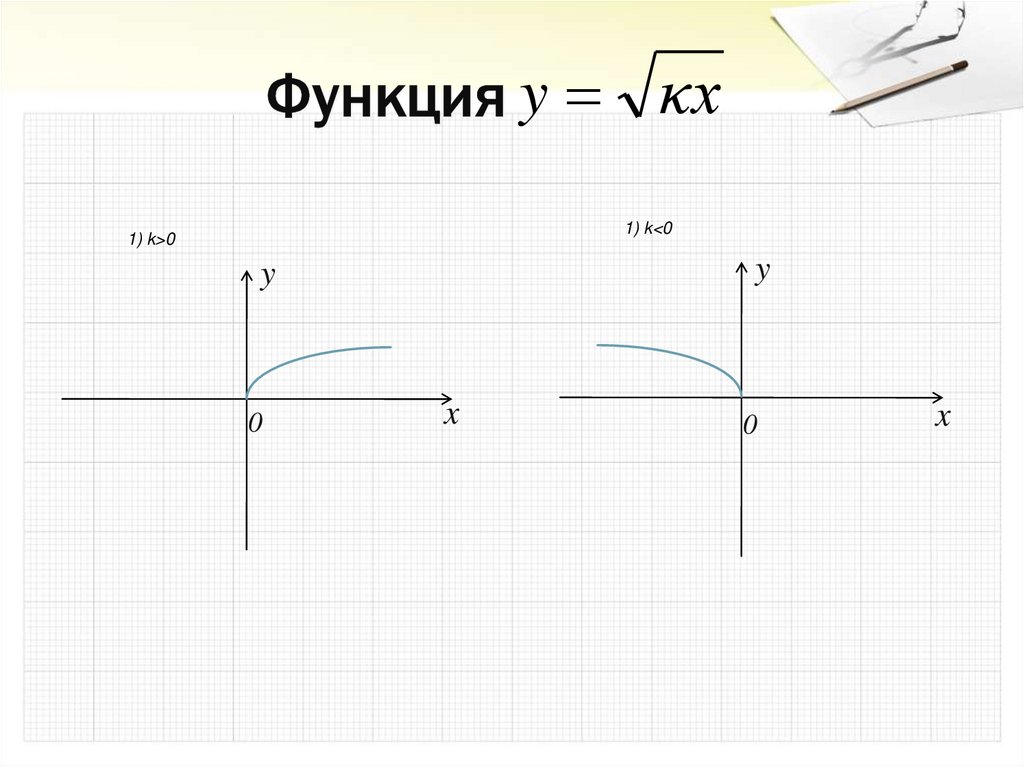
19. Функция

y κx
1) k<0
1) k>0
y
y
0
x
0
x

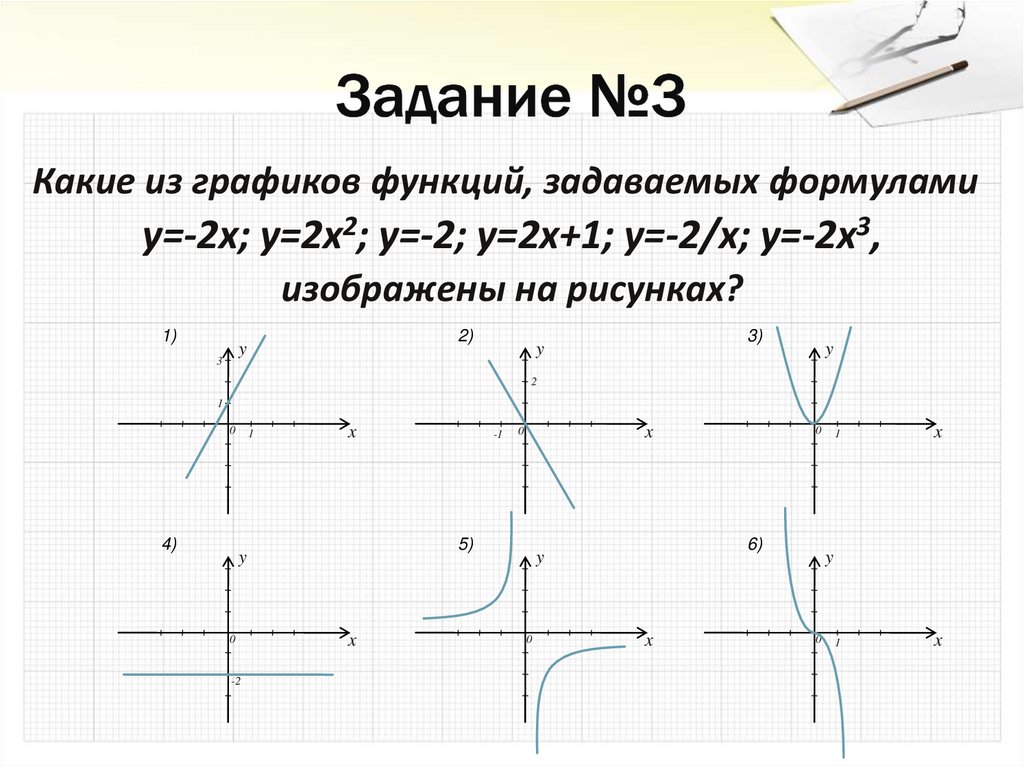
20. Задание №3

Какие из графиков функций, задаваемых формулами
y=-2x; y=2x2; y=-2; y=2x+1; y=-2/x; y=-2x3,
изображены на рисунках?
1)
2)
y
3
3)
y
y
2
1
0
4)
1
x
-2
x
0
5)
y
0
-1
x
6)
y
0
0
x
1
x
1
x
y
0

21. Вопросы на повторение:

1.
Графиком линейной функции является _______________ .
2.
Графиком квадратичной функции является _______________ .
3.
Если в квадратичной функции коэффициент а >0, то ветви параболы направлены______ .
4.
Если в квадратичной функции коэффициент а <0, то ветви параболы направлены ______ .
5.
Если при решении квадратного уравнения D >0, то парабола пересекает ось Ох в __ точках.
6.
Если при решении D=0, то точка пересечения параболы и оси Ох является _____ параболы.
7.
Графиком обратной пропорциональности является _________________ .
8.
Если k >0 в уравнении, то ветви гиперболы расположены в __ четверти и в __ четверти.
9.
Если k <0 в уравнении, то ветви гиперболы расположены в __ четверти и __ четверти.

22. Рассмотрим основные правила преобразования графиков на примерах элементарных функций

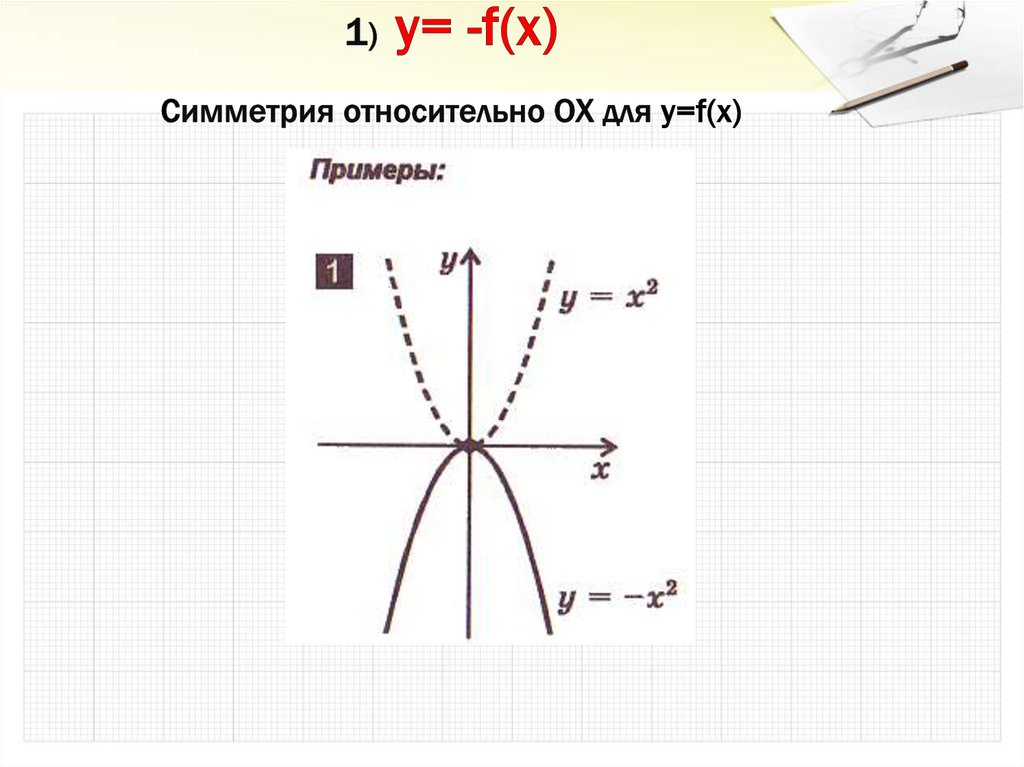
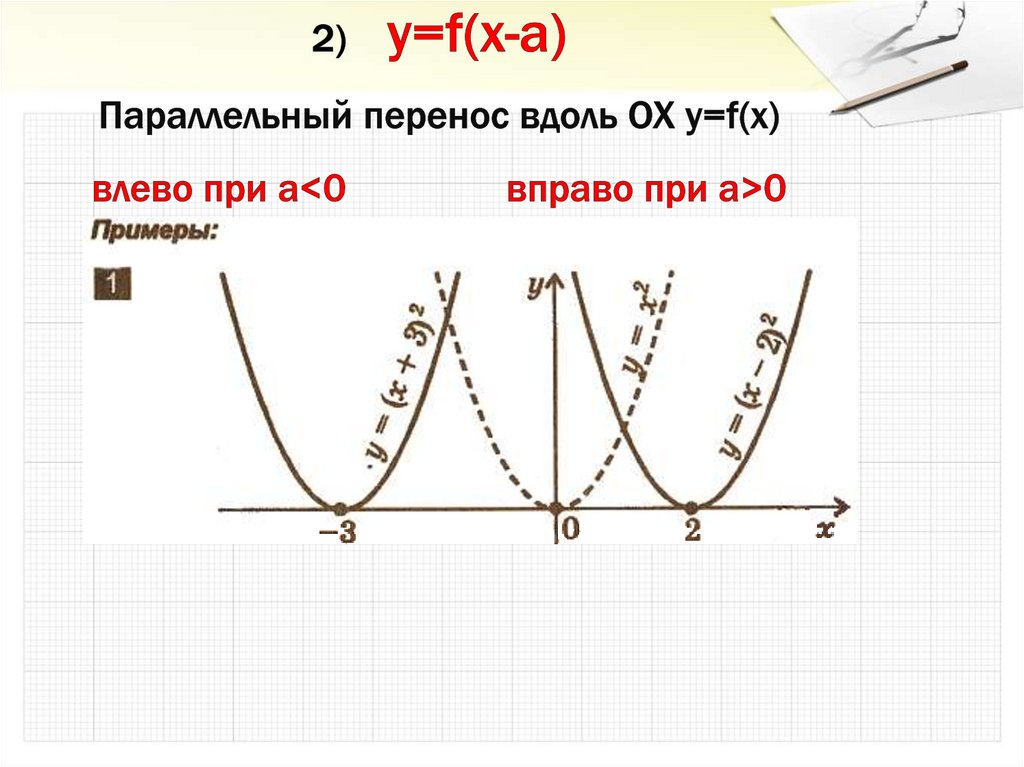
23. 1) y= -f(x) Cимметрия относительно OX для y=f(x)

24. 2) y=f(x-a) Параллельный перенос вдоль OX y=f(x) влево при a<0 вправо при a>0

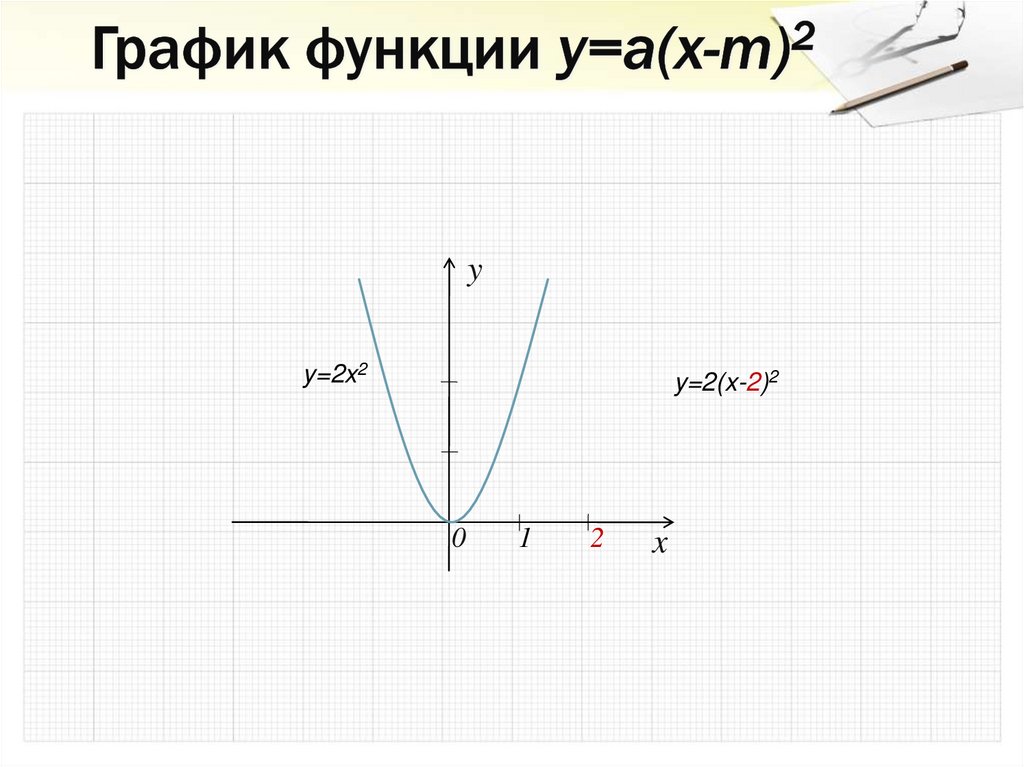
25. График функции y=a(x-m)2

y
y=2x2
y=2(x-2)2
0
1
2
x

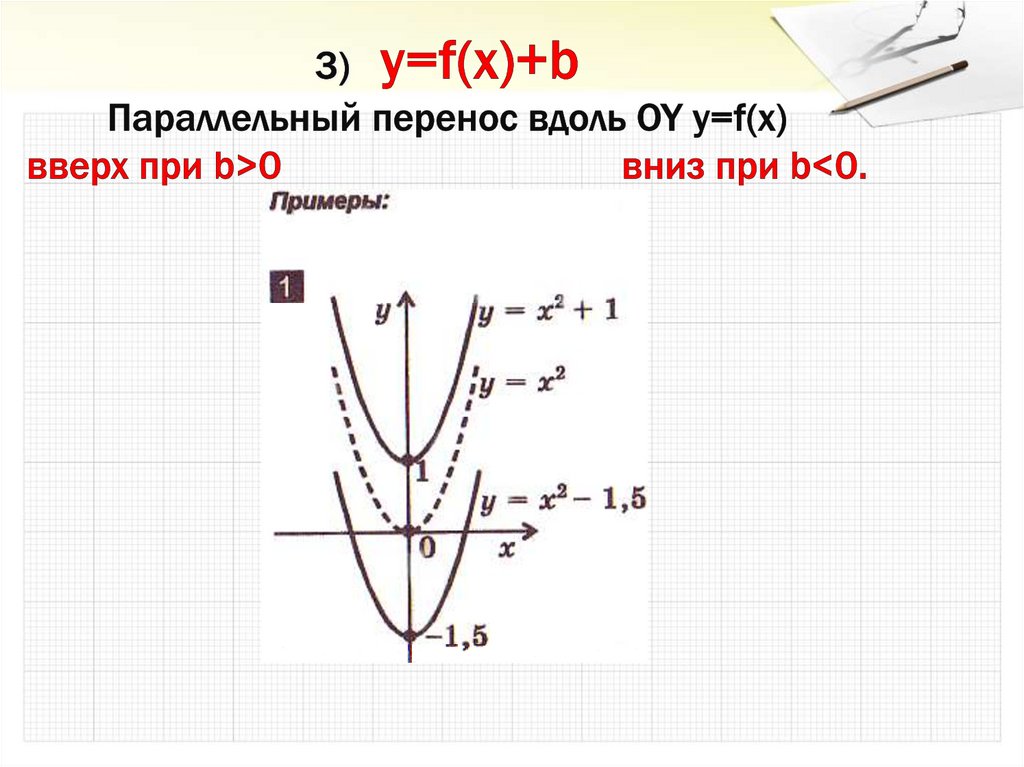
26. 3) y=f(x)+b Параллельный перенос вдоль OY y=f(x) вверх при b>0 вниз при b<0.

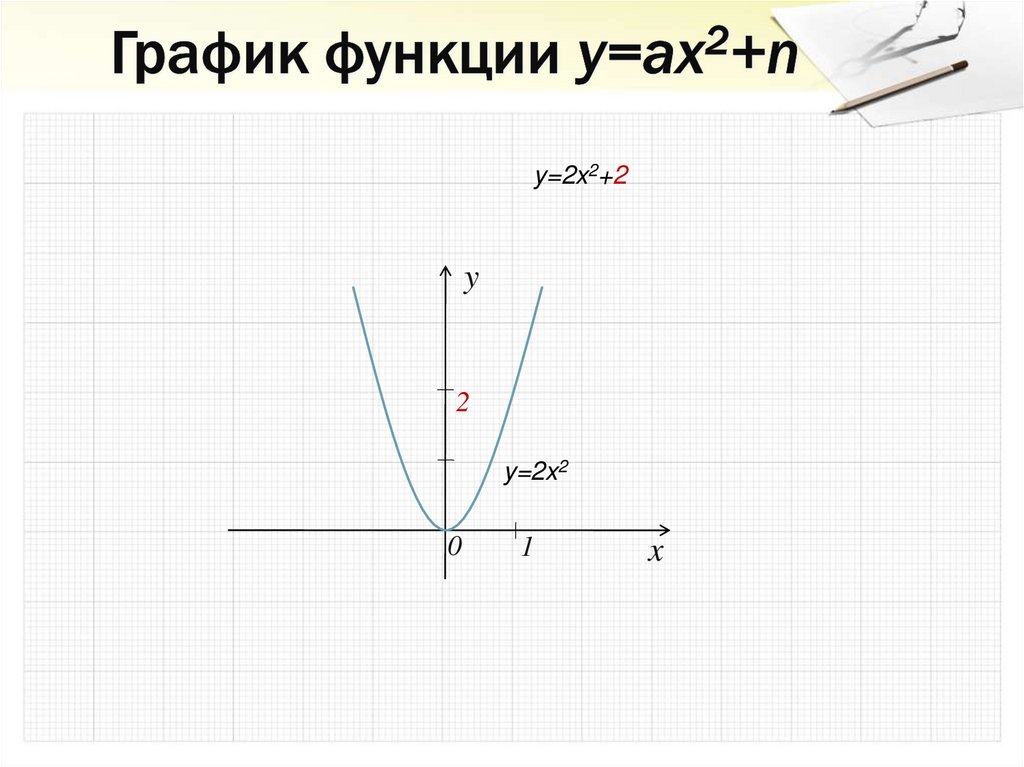
27. График функции y=ax2+n

y=2x2+2
y
2
y=2x2
0
1
x

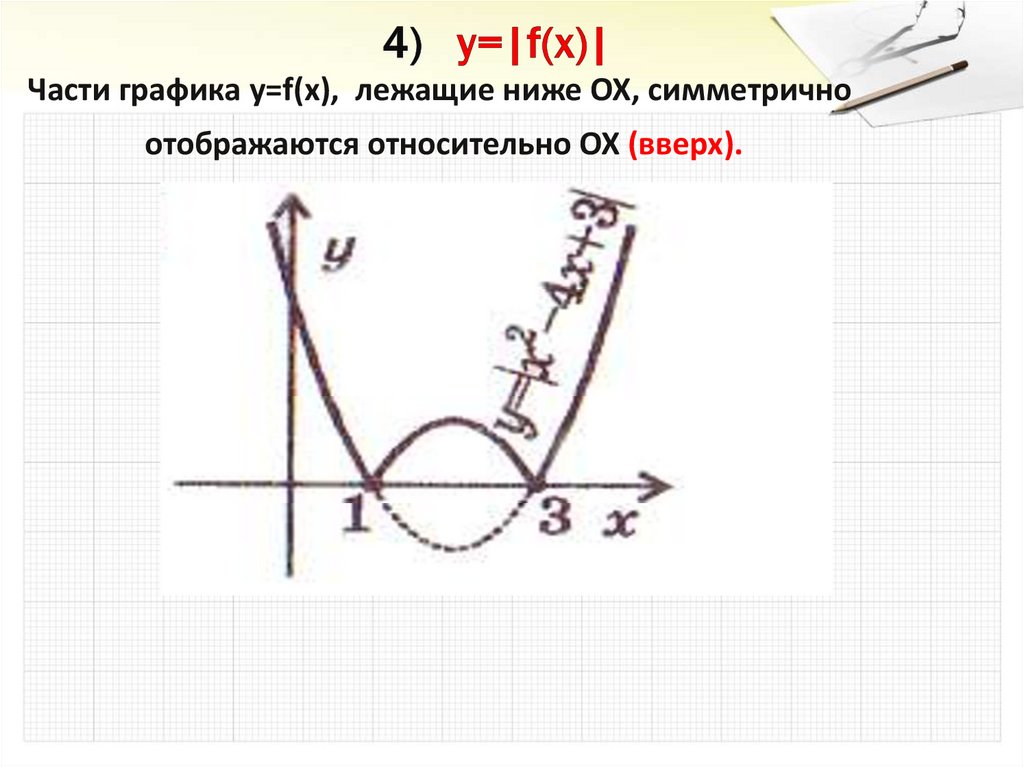
28. 4) y=|f(x)|

Части графика y=f(x), лежащие ниже OX, симметрично
отображаются относительно OX (вверх).

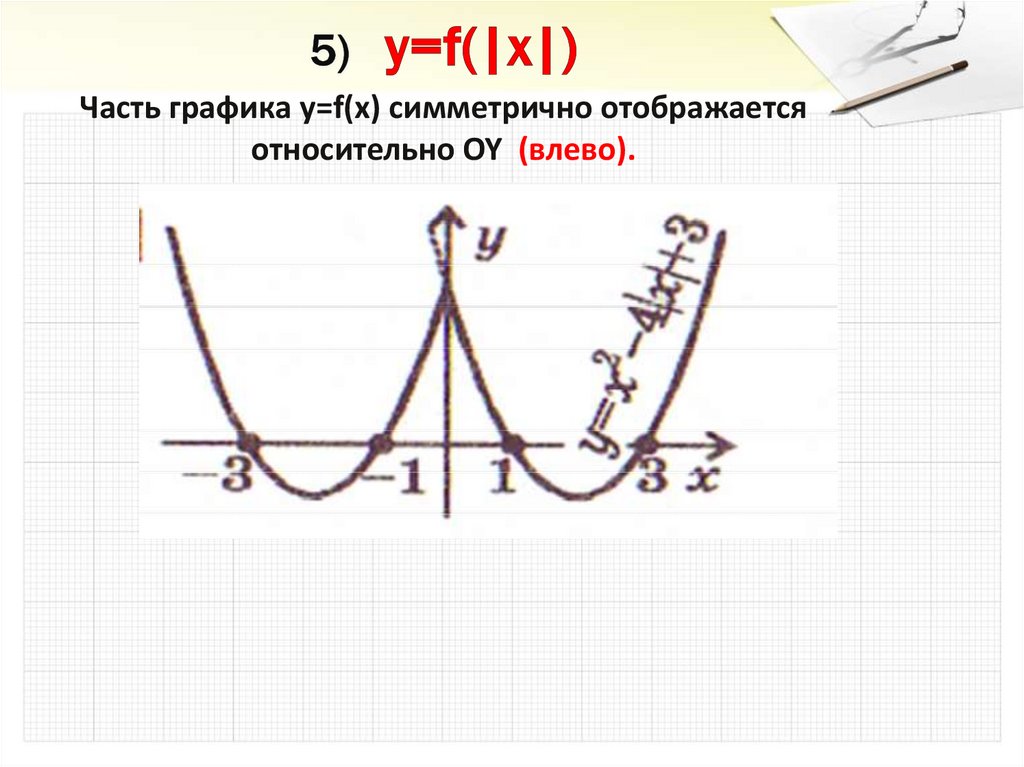
29. 5) y=f(|x|)

Часть графика y=f(x) симметрично отображается
относительно OY (влево).

30. Задание №4

С помощью шаблона параболы y=x2 постройте
графики функций y=-x2-2; y=(x+4)2; y=(x-3)2-4.