Similar presentations:
Функции и их свойства
1.
2.
Функция у=f(x) –зависимость по которой каждому значению независимой
переменной соответствует единственное значение другой
зависимой переменной.
Переменная, значение которой выбирается произвольно, называется
независимой
независимойпеременной
переменной, а переменная, которая определяется
по некоторому правилу, называютзависимой
зависимойпеременной
переменной.
Независимая переменная – аргумент.
Зависимая переменная – функция или значение аргумента.
.
независимая
переменная
у=f(x)
g=f(t)
зависимая переменная
x
у
t
g
3.
График функции- множество всех точек координатной плоскости, абсциссы
которых равны значениям аргумента, а ординаты –
соответствующим значениям функции.
40
30
20
10
0
-12
-10
-8
-6
-4
-2
-10
-20
-30
-40
0
2
4
6
8
4.
Способы задания функции1. Аналитический (с помощью формулы)
1) Длина прямоугольника х см, а ширина на 5
см меньше, выразите периметр у. Получим:
у=2х+2(х-5)
у=4х-10
2) Длина прямоугольника х см, а ширина на 6
см больше, выразите периметр у. Получим:
у=2х+2(х+6)
у=4х+12
5.
Способы задания функции2. Табличный
Отец старше сына на 20 лет, заполните таблицу. Запишите
зависимость возраста отца от возраста сына.
y – возраст отца, x – возраст сына y=20+x
y – возраст сына, x – возраст отца y=x-20
отец 35
45
75
31
60
38
57
сын 15
25
55
11
40
18
37
6.
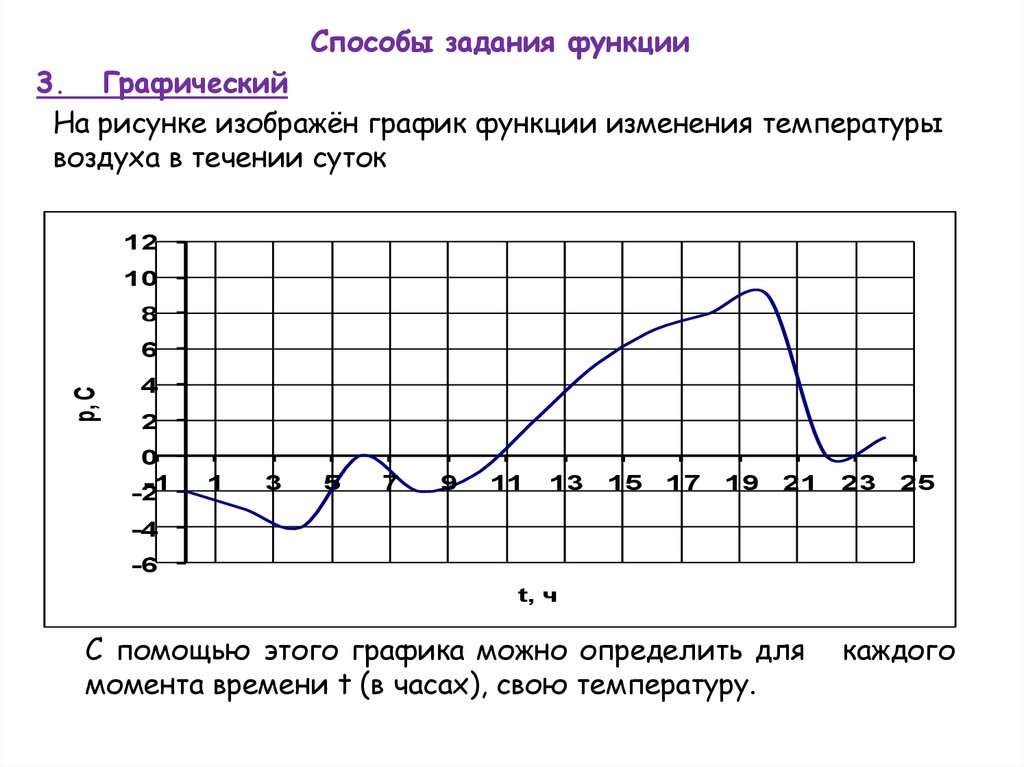
Способы задания функции3. Графический
На рисунке изображён график функции изменения температуры
воздуха в течении суток
12
10
8
p, C
6
4
2
0
-1
-2
1
3
5
7
9
11
13
15
17
19
21
23
25
-4
-6
t, ч
С помощью этого графика можно определить для
момента времени t (в часах), свою температуру.
каждого
7. 4. Словесный
Способы задания функции4. Словесный
Функцию у=2х можно
словесным описанием:
задать
следующим
каждому действительному значению аргумента х
ставится в соответствие его удвоенное значение
8. Основные определения и свойства функций
9.
Область определения функции –это те значения, которые может принимать независимая
переменная ( х)
Обозначение: D(f).
10. Область определения функции
ух3
х1
х2
0
х4 х
Областью определения функции называется
множество всех значений независимой переменной х.
Обозначение: D(f).
11.
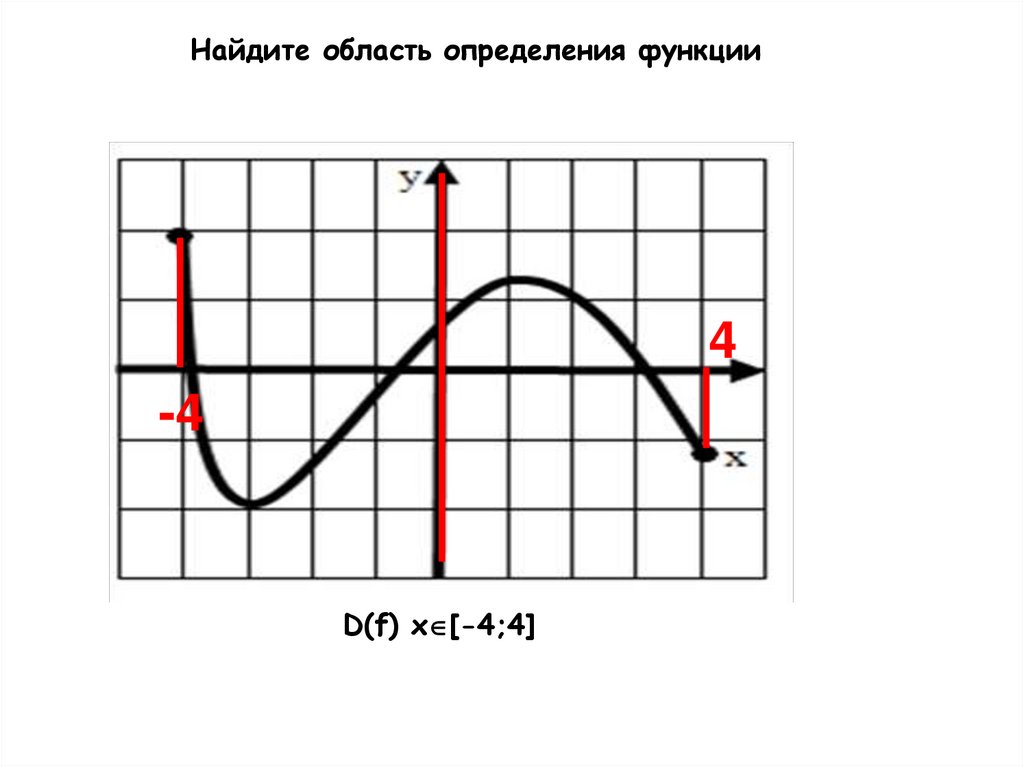
Найдите область определения функции4
-4
D(f) x [-4;4]
12.
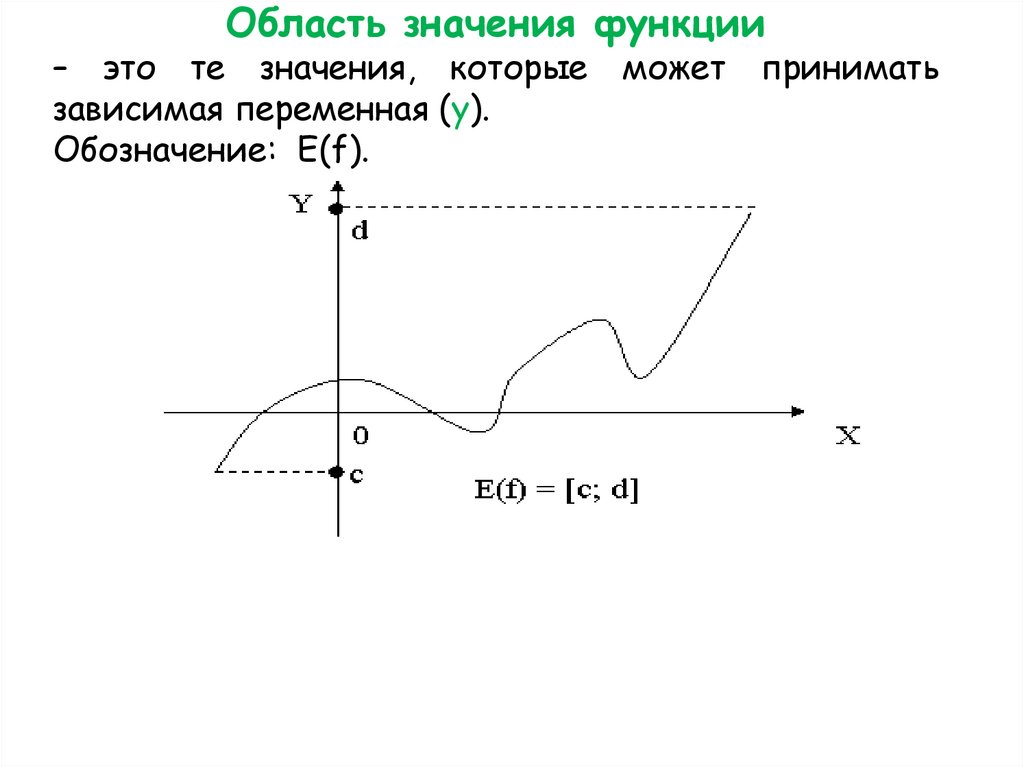
Область значения функции– это те значения, которые
зависимая переменная (y).
Обозначение: E(f).
может принимать
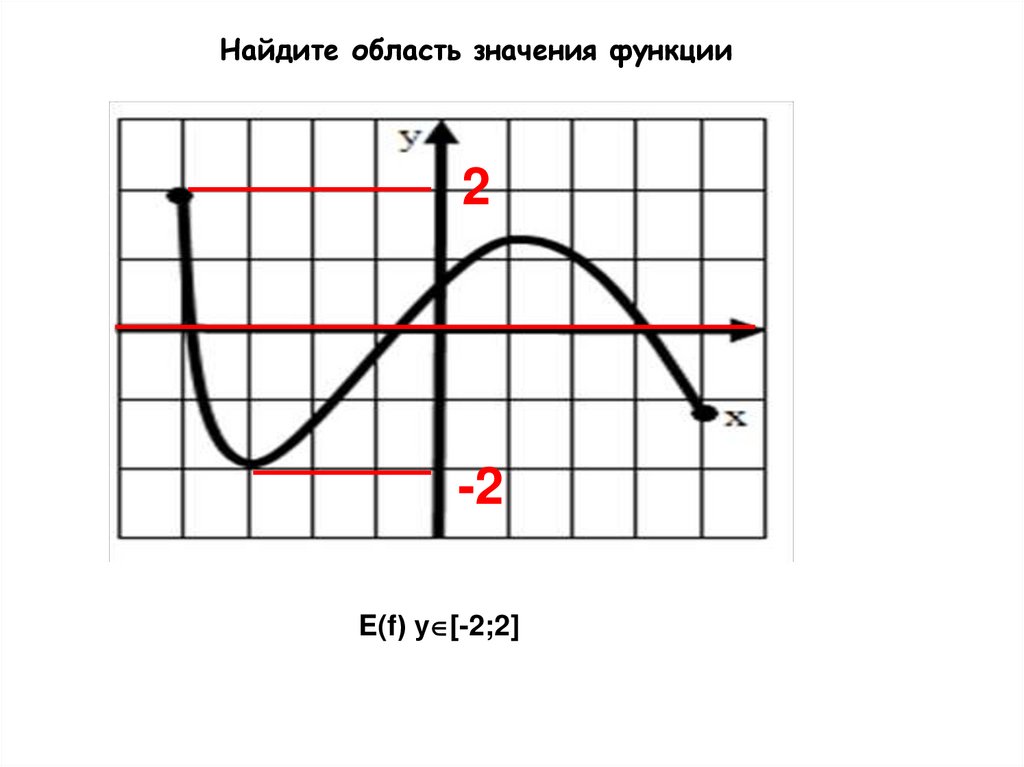
13.
Найдите область значения функции2
-2
E(f) у [-2;2]
14.
Функция у=f(x) называется чётной функцией, если выполняютсядва условия:
1) область определения функции – симметричное множество
относительно числа 0.
(Симметричным множеством чисел называется множество, где с
каждым числом х, присутствует и число –х.)
2) выполняется равенство f (-x) = f (x)
-2 и 2 принадлежат D(f)
6
f(-2)=4
4
f(2)=4
f (-x) = f (x)
2
6
6
4
2
0
x
2
4
График чётной функции расположен
симметрично относительно оси
ординат.
6
6
15.
Функция у=f(x) называется нечётной функцией, есливыполняются два условия:
1) область определения функции – симметричное
множество относительно числа 0.
2) выполняется равенство f(-x) = -f(x)
y=x3
10
0
D(f) (- ;+ )
5
6
4
f(-x) = (-x)3=-x3= -f(x)
0
2
2
4
6
5
0
График нечётной функции
расположен симметрично
относительно начала координат.
10
6
x
6
16. Выполните устно
1. Функция f (x) – четная,f ( 3 ) = 25 , тогда f ( -3 ) =25?
71
f ( -8 ) = 71, тогда f ( 8 ) = ?
2.Функция g ( x ) – нечетная,
g ( 7 ) = 43, тогда g ( -7 ) =-43
?
g ( - 2 ) = -64, тогда g ( 2 ) =64
?
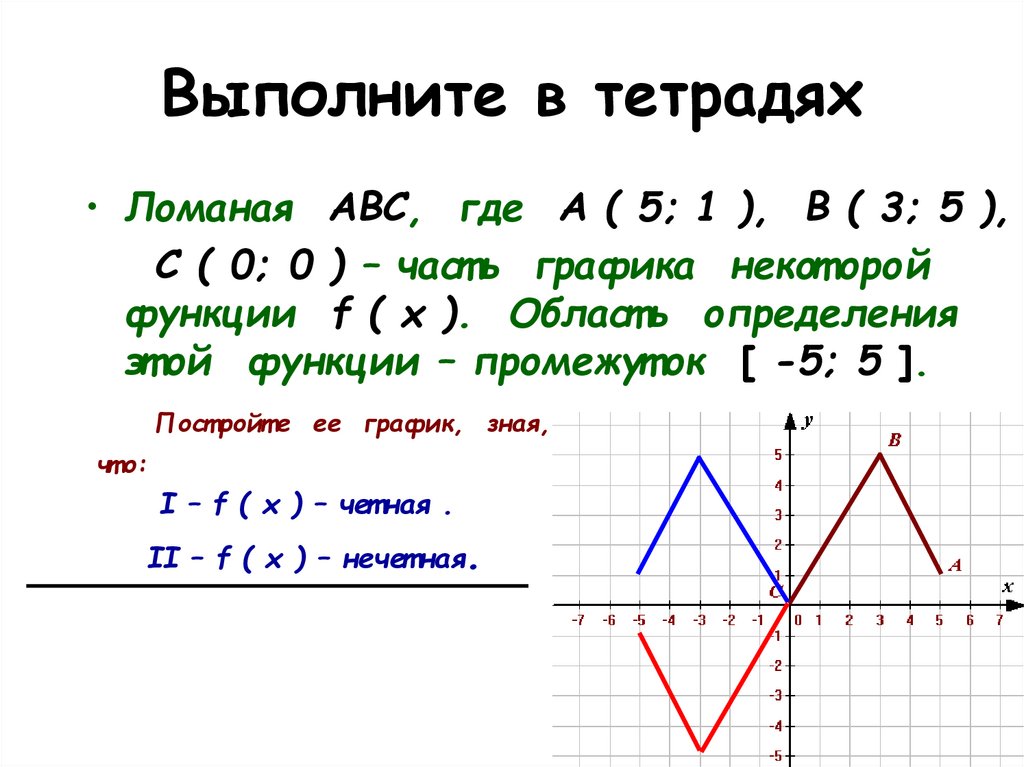
17. Выполните в тетрадях
• Ломаная АВС, где А ( 5; 1 ), В ( 3; 5 ),С ( 0; 0 ) – част ь графика некот орой
функции f ( x ). Област ь определения
эт ой функции – промежут ок [ -5; 5 ].
Пост ройт е ее график, зная,
чт о:
I – f ( x ) – чет ная .
II – f ( x ) – нечет ная.
18.
Нули функции– это те значения переменной, при которых значения функции
равны нулю f(x)=0.
Нули функции так же называют корнями функции.
Функция может иметь несколько нулей.
y=x(x+1)(x-3)
x(x+1)(x-3)=0
x=0, x=-1, x=3.
19.
Графически нуль функции– это абсцисса точки пересечения графика функции с осью
абсцисс.
На рис. представлен график функции y=x(x+1)(x-3) x [-2;2]
с нулями: x=-1, x=3 и x=0 .
10
10
5
x ( x 3) ( x 1)
А(-1;0)
-1
3
2
B(0;0)
0
1
0
5
10
10
C(3;0)
3
1
2
3
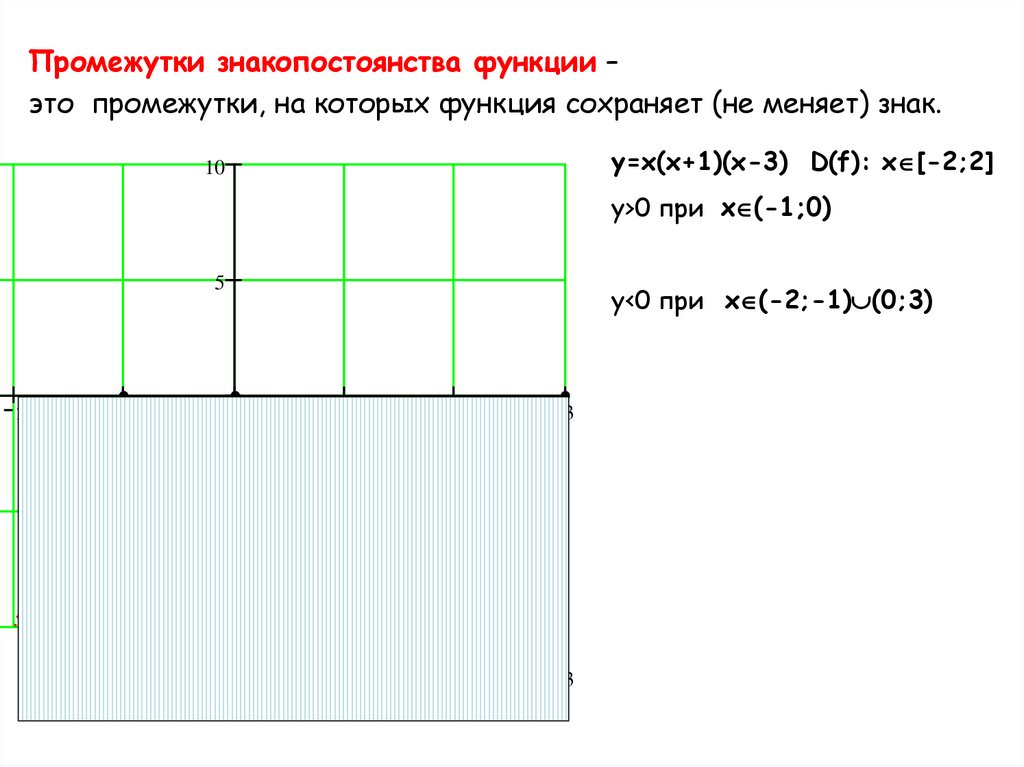
20.
Промежутки знакопостоянства функции –это промежутки, на которых функция сохраняет (не меняет) знак.
y=x(x+1)(x-3) D(f): x [-2;2]
10
y>0 при x (-1;0)
5
2
1
y<0 при x (-2;-1) (0;3)
0
1
2
3
5
10
x
3
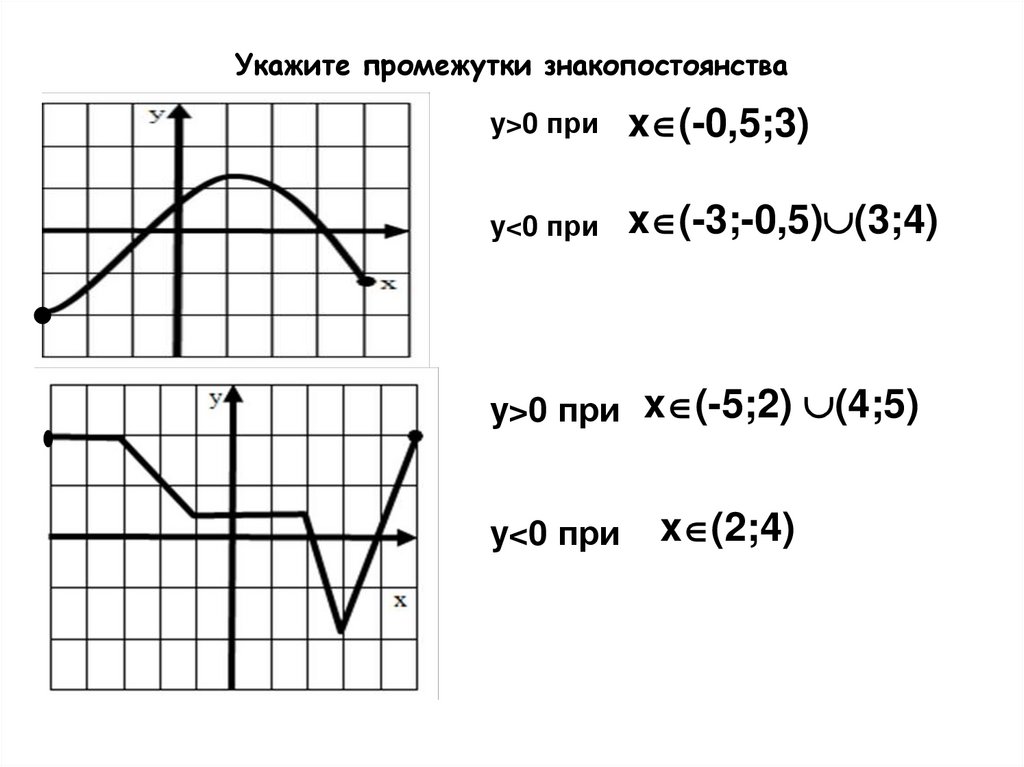
21. Укажите промежутки знакопостоянства
y>0 приx (-0,5;3)
y<0 при
x (-3;-0,5) (3;4)
y>0 при x (-5;2) (4;5)
y<0 при
x (2;4)
22.
Функция f(x) называется возрастающей на промежутке X, если-большему значению аргумента соответствует большее значение
функции.
- для любых двух значений аргумента x1 и x2 из этого
промежутка, таких что x2 > x1 следует f(x2)>f(x1).
10
f(x25)
x1
f(x2)
x2
x1
4
2
0
x2
2
4
f(x1)
f(x1)
5
x2 > x1
x2 > x1 f(x2)>f(x1)
f(x2) > f(x1)
10
x [-3;1,8]
x D(f)
x
5
23.
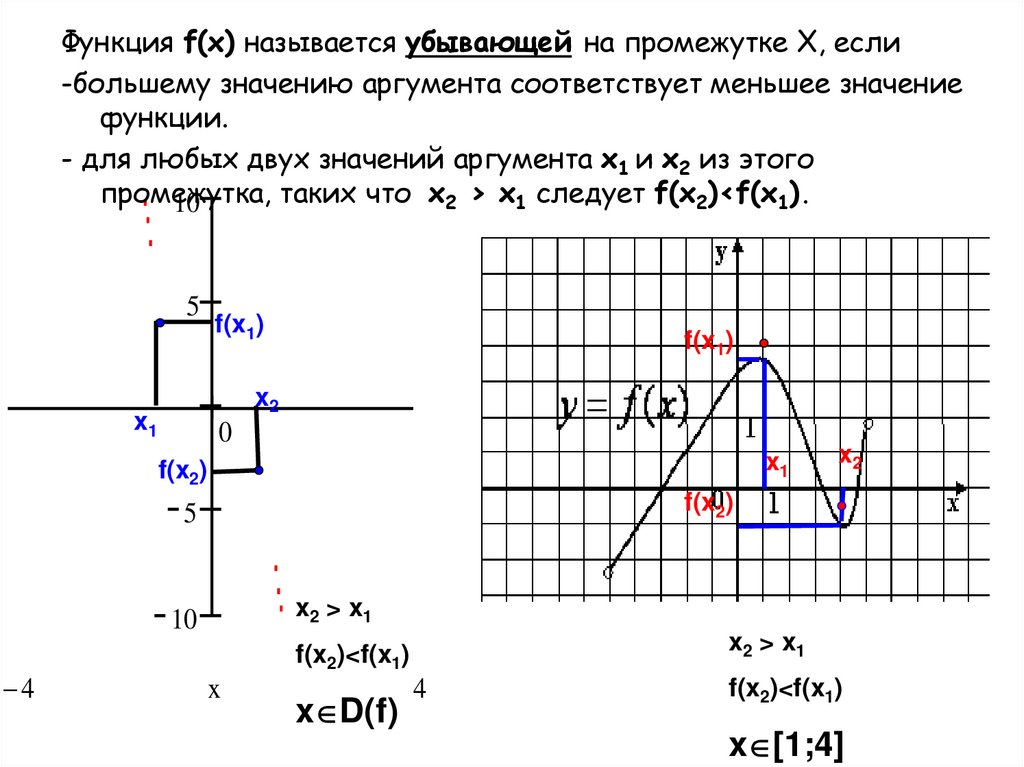
Функция f(x) называется убывающей на промежутке X, если-большему значению аргумента соответствует меньшее значение
функции.
- для любых двух значений аргумента x1 и x2 из этого
промежутка,
таких что x2 > x1 следует f(x2)<f(x1).
10
5
f(x1)
f(x1)
x2
x1
0
x1
f(x2)
f(x2)
5
x2 > x1
10
4
x2
x2 > x1
f(x2)<f(x1)
x
x D(f)
4
f(x2)<f(x1)
x [1;4]
24. Промежутки возрастания и убывания называют промежутками монотонностями
25.
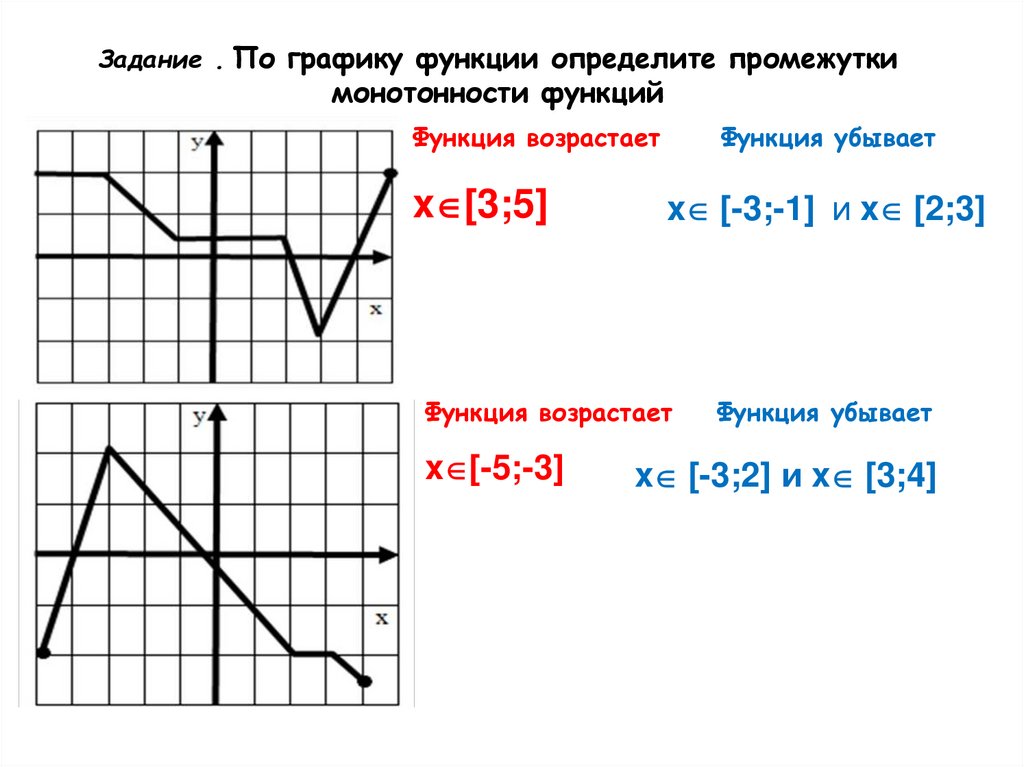
Задание . По графику функции определите промежуткимонотонности функций
Функция возрастает
x [3;5]
Функция убывает
x [-3;-1] и x [2;3]
Функция возрастает
x [-5;-3]
Функция убывает
x [-3;2] и x [3;4]
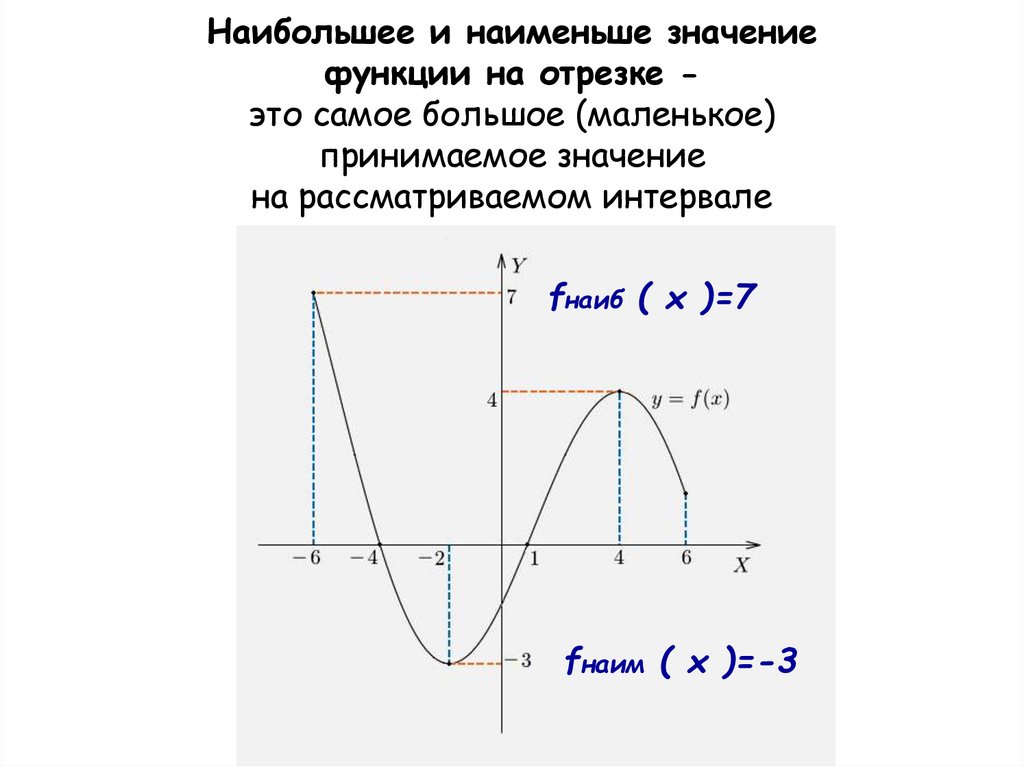
26. Наибольшее и наименьше значение функции на отрезке - это самое большое (маленькое) принимаемое значение на рассматриваемом
Наибольшее и наименьше значениефункции на отрезке это самое большое (маленькое)
принимаемое значение
на рассматриваемом интервале
fнаиб ( x )=7
fнаим ( x )=-3
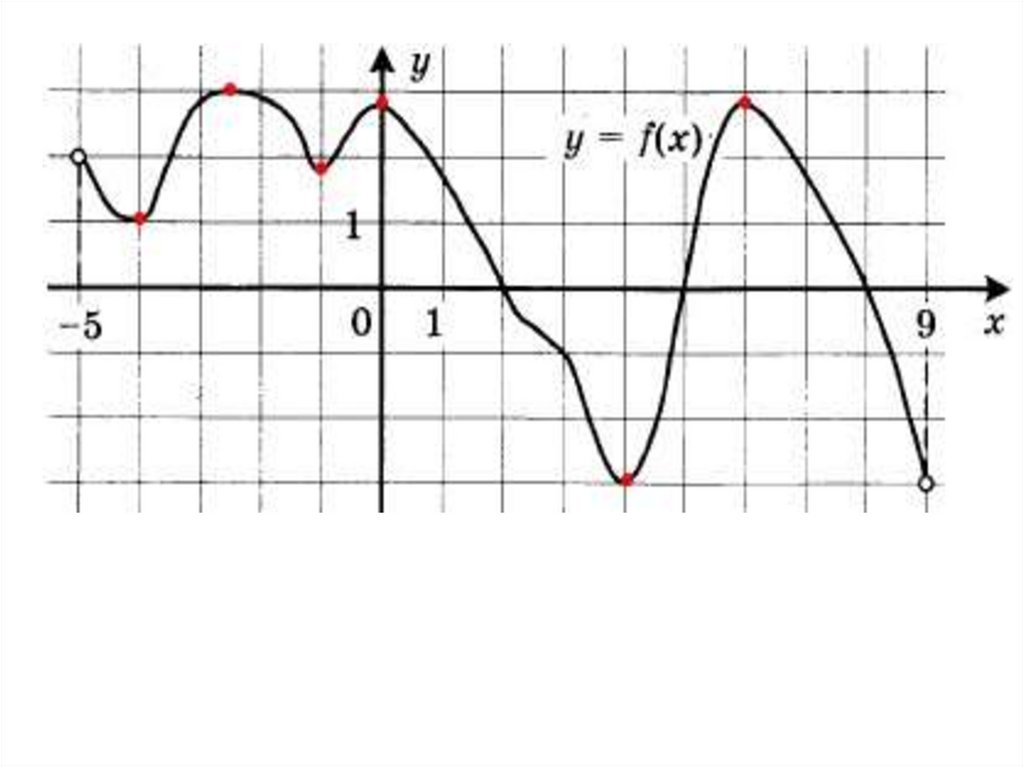
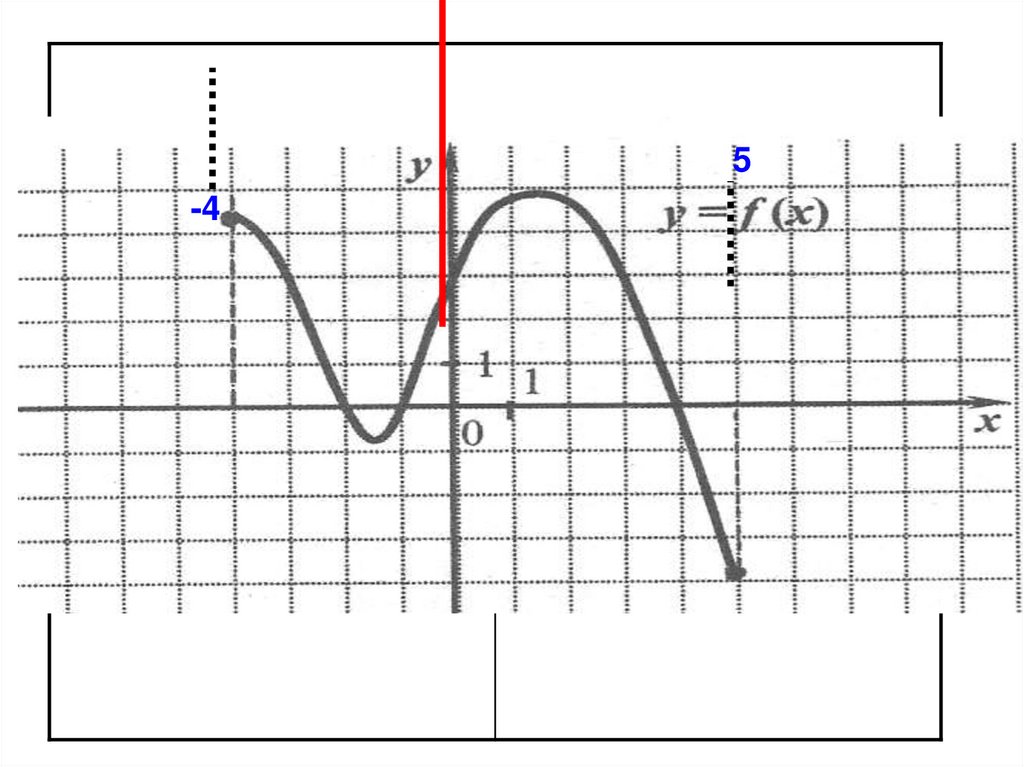
27. Укажите наибольшее и наименьшее значение функции на заданном отрезке
28.
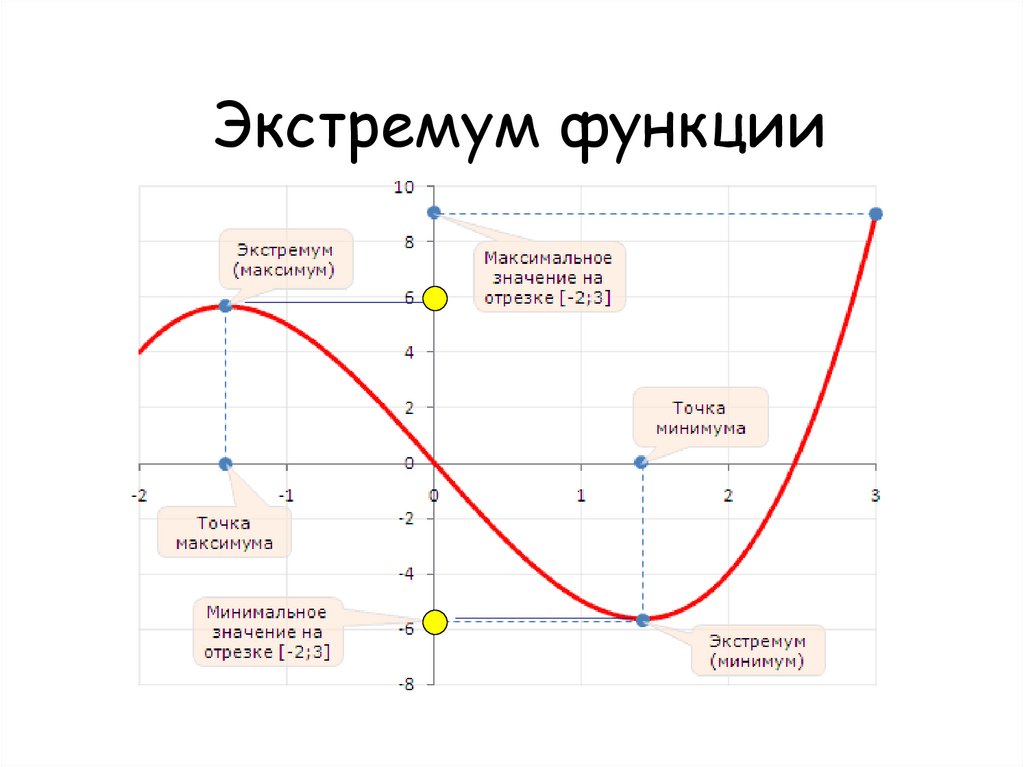
29. Точки максимума и минимума (точки экстремума)
30.
31.
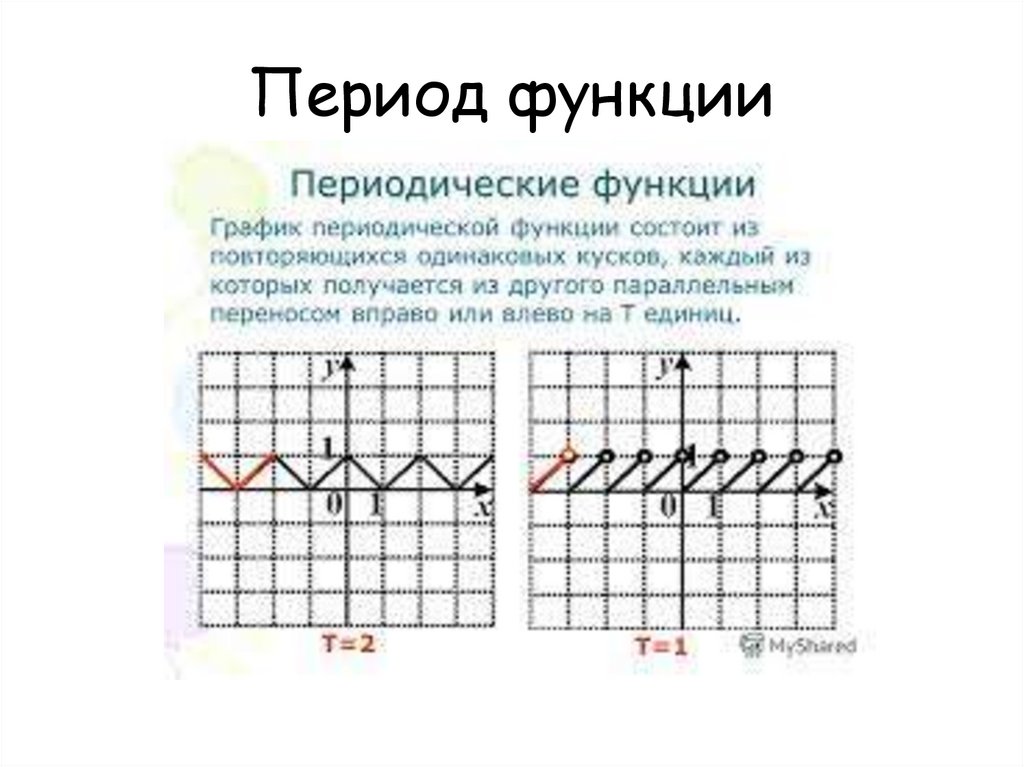
Экстремум функции32. Период функции
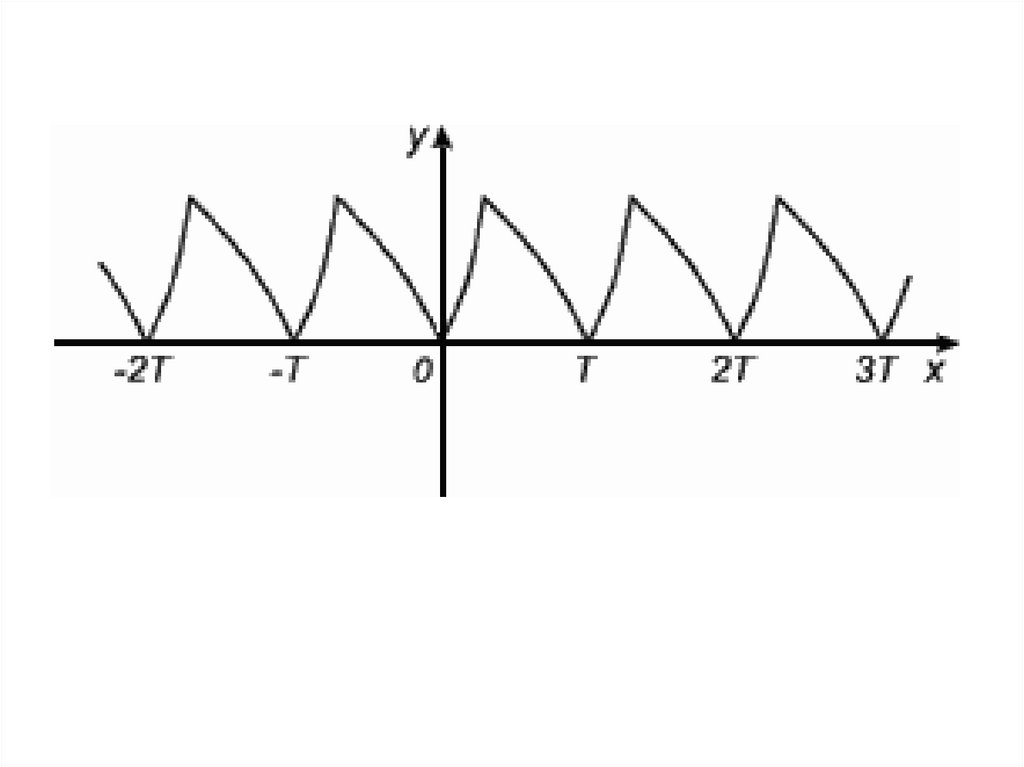
33.
34.
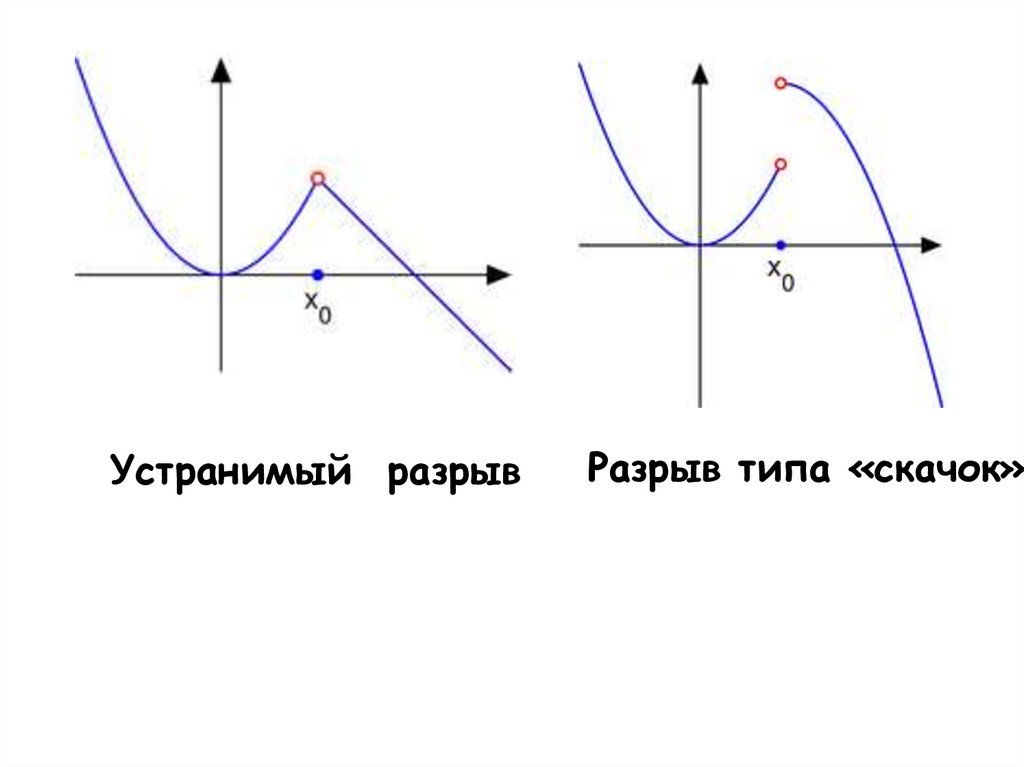
35. Непрерывность функции
С- точка разрыва функции36.
Устранимый разрывРазрыв типа «скачок»
37.
Х=0 - точка разрыва38.
Схема элементарного исследования функции1. Область определения (D(f)=…) и область значения (Е(f)=…);
2. Четность / нечетность. Функция является чётной, нечетной или
ни чётной ни нечётной (общего вида);
3. Периодичность функции (Т= …. );
4. Непрерывность .
5. Нули функции (графически – точки пересечения с осью Х) ;
6. Промежутки знакопостоянства функции;
7. Промежутки возрастания и убывания функции;
8. Наибольшее (наименьшее) значение функции на отрезке;
9. Точки экстремума (точки максимума и минимума)
10. Экстремум функции.
39.
5-4
40.
41.
42. Задание . Установите соответствие
13
2
4
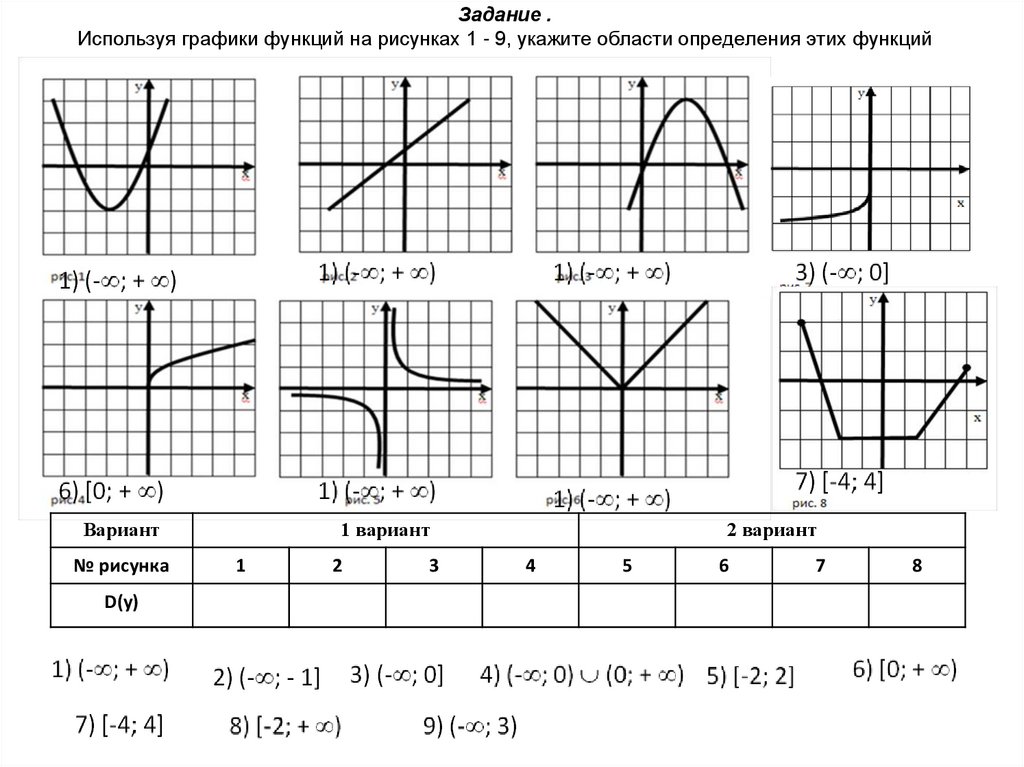
43. Задание . Используя графики функций на рисунках 1 - 9, укажите области определения этих функций
Вариант№ рисунка
D(у)
1 вариант
1
2
3
2 вариант
4
5
6
7
8
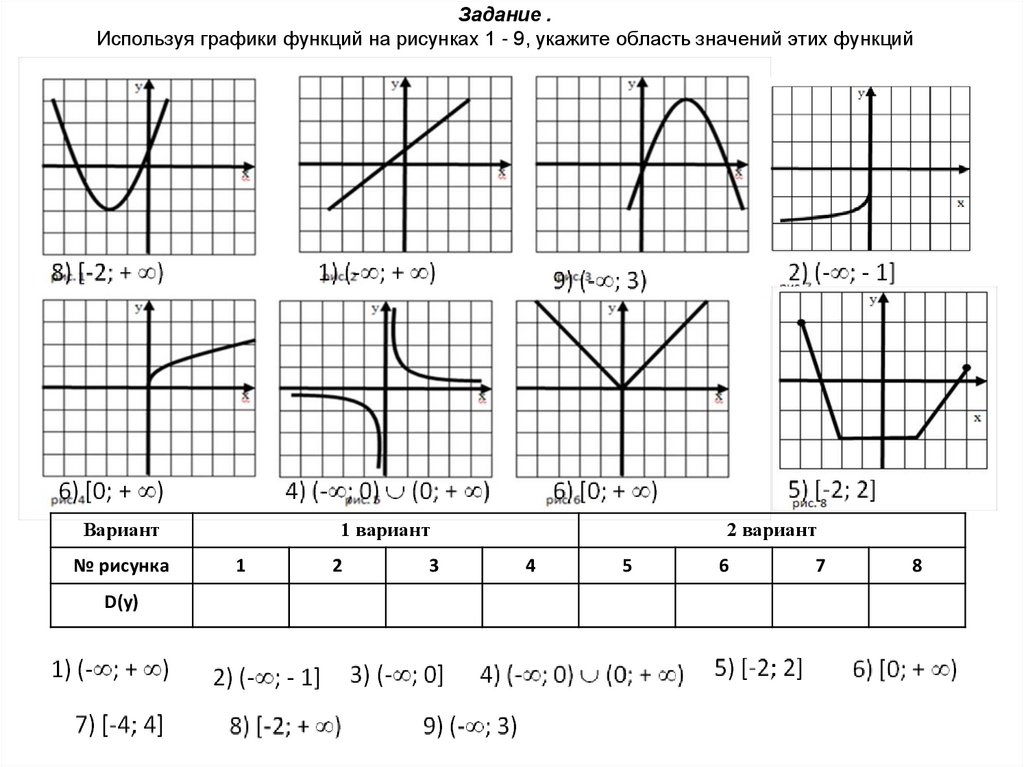
44. Задание . Используя графики функций на рисунках 1 - 9, укажите область значений этих функций
Вариант№ рисунка
D(у)
1 вариант
1
2
3
2 вариант
4
5
6
7
8


























 mathematics
mathematics