Функции и их свойства

1. Тема: Функции и их свойства

y
c
Тема:
Функции
и их свойства
y
0
x
xв
у в x1
x
x2

2.

Определение
Обозначение функции
у( х ) - функция
х - аргумент
зависимая переменная
независимая
переменная

3.

(х; у)- координаты точки в плоскости
у – ордината точки
(координата оси ОУ)
у( х )- функция
х – абсцисса точки
(координата оси ОХ)
х - аргумент

4. Свойства функции

Область
Все значения которые принимает независимая переменная –
определения D(х) аргумент х
Область
значения E(у)
Все допустимые значения которые принимает зависимая
переменная функция у
Промежутки
возрастания и
убывания
f(х) – возрастает, если наибольшему значению аргумента х
соответствует наибольшее значение функции f(х)
f(х) – убывает, если наибольшему значению аргумента х
соответствует наименьшее значение функции f(х)
Промежутки
Все значения аргумента х при которых функция принимает
знакопостоянства положительные значения у>0 или отрицательные значения у<0
Нули функции
Четность и
нечетность
функции
Ограниченность
Значения аргумента х, при котором значение функции равно
нулю ( у = 0).
f(х)–четная, если f(-х)=f(х), график четной фун.симметричен оси
ОУ
f(х) – нечетная, если f(-х) = - f(х), график нечетной функции
симметричен начала координат
Функция у = f(х) ограниченна снизу на множестве Х, если все
значения функции на множестве Х больше некоторого числа.
Функция у = f(х) ограниченна сверху на множестве Х, если все
значения функции на множестве Х меньше некоторого числа.

5.

Наибольшее и
наименьшее
значение функции
Непрерывность
Выпуклость
функции
Наибольшее значение функции – это число M= f(х0), такое
что f(х) ≤ f(х0)
Наименьшее значение функции - это число m= f(х0), такое
что f(х) ≥ f(х0)
Функция непрерывна на промежутке, если она
определена на этом промежутке и непрерывна
в каждой точке этого промежутка.
Непрерывность функции на промежутке Х
означает, что график функции на всей области
определения сплошной.
Функция выпукла вниз на промежутке Х если,
соединив любые две точки ее графика отрезком
прямой, мы обнаружим, что соответствующая
часть графика лежит ниже проведенного отрезка.
Функция выпукла вверх на промежутке Х, если соединив
любые две точки ее графика отрезком прямой,
мы обнаружим, что соответствующая часть
графика лежит выше проведенного отрезка .

6.

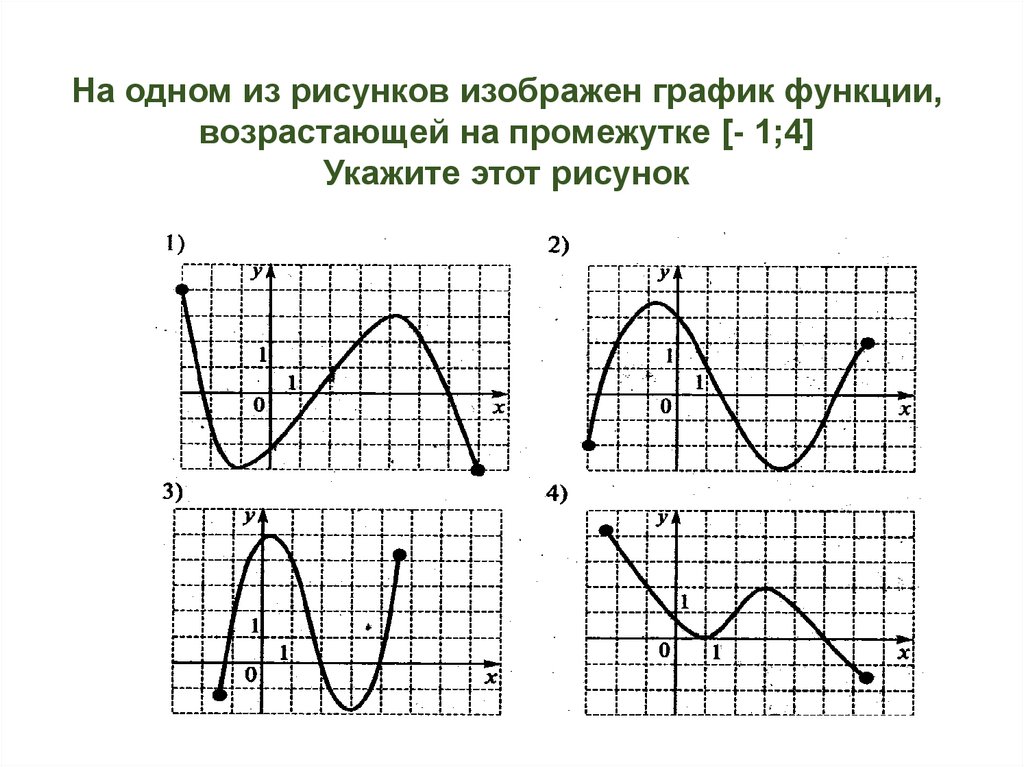
На одном из рисунков изображен график функции,
возрастающей на промежутке [- 1;4]
Укажите этот рисунок

7. На одном из рисунков изображен график функции, убывающей на промежутке [0 ; 3 ]. Укажите этот рисунок.

8.

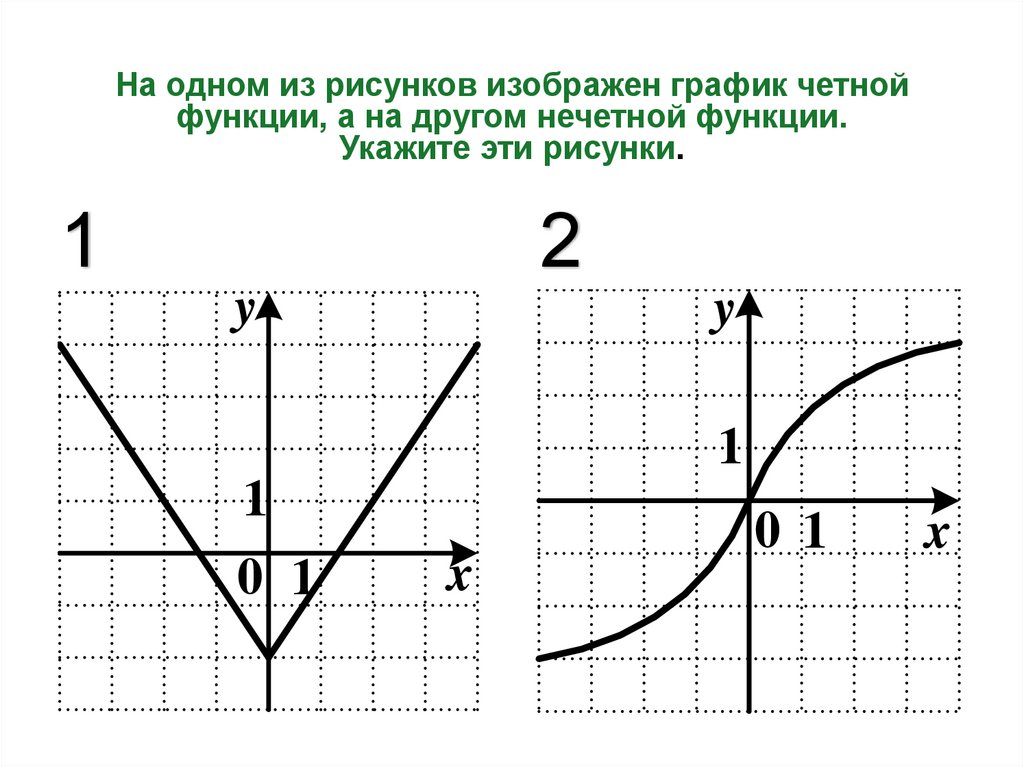
На одном из рисунков изображен график четной
функции, а на другом нечетной функции.
Укажите эти рисунки.
1
2
y
y
1
1
0 1
x
0 1
x

9.

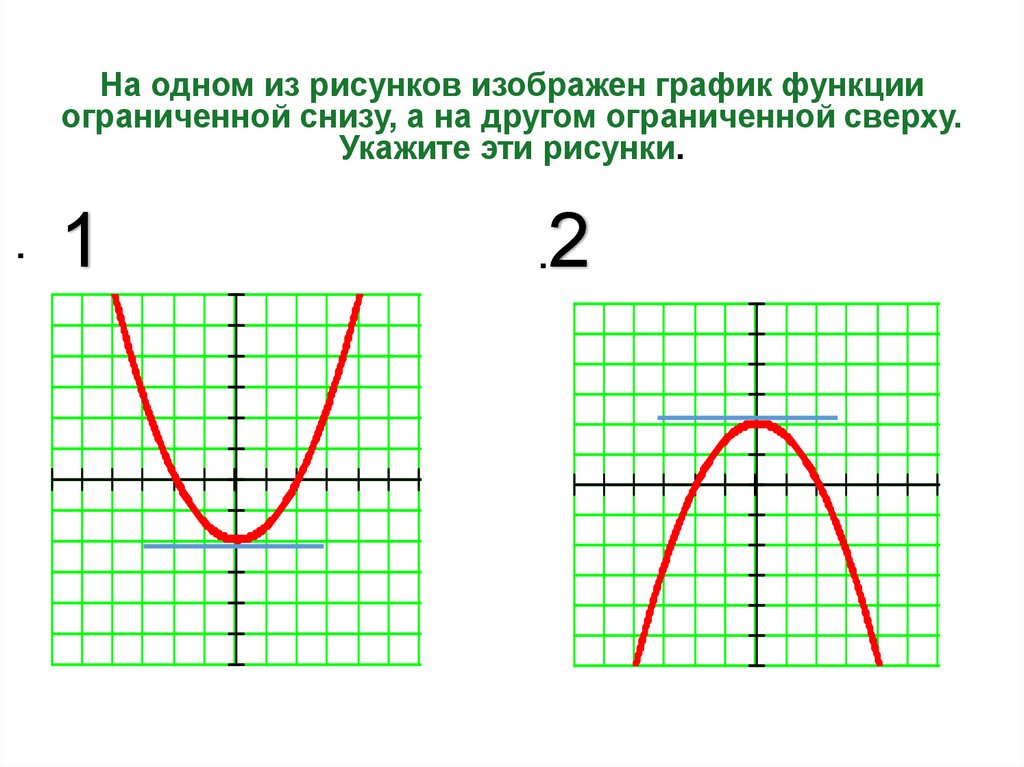
На одном из рисунков изображен график функции
ограниченной снизу, а на другом ограниченной сверху.
Укажите эти рисунки.
1
2

10.

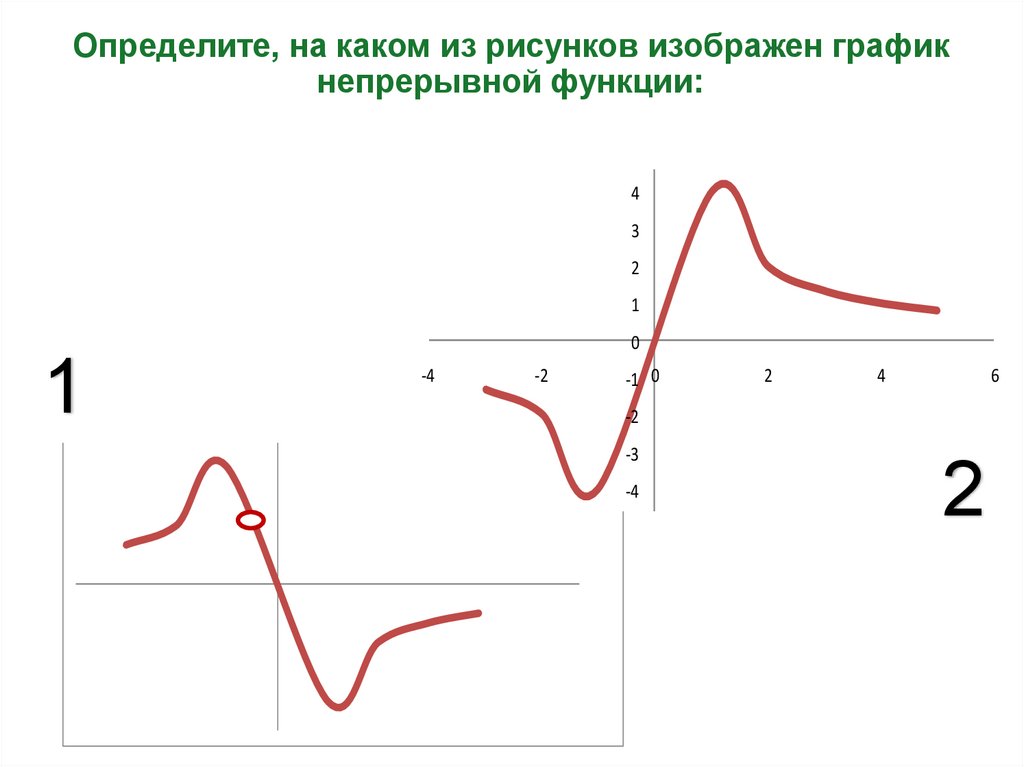
Определите, на каком из рисунков изображен график
непрерывной функции:
5
4
3
2
1
0
1
-4
-2
-1 0
2
4
6
-2
-3
-4
-5
2

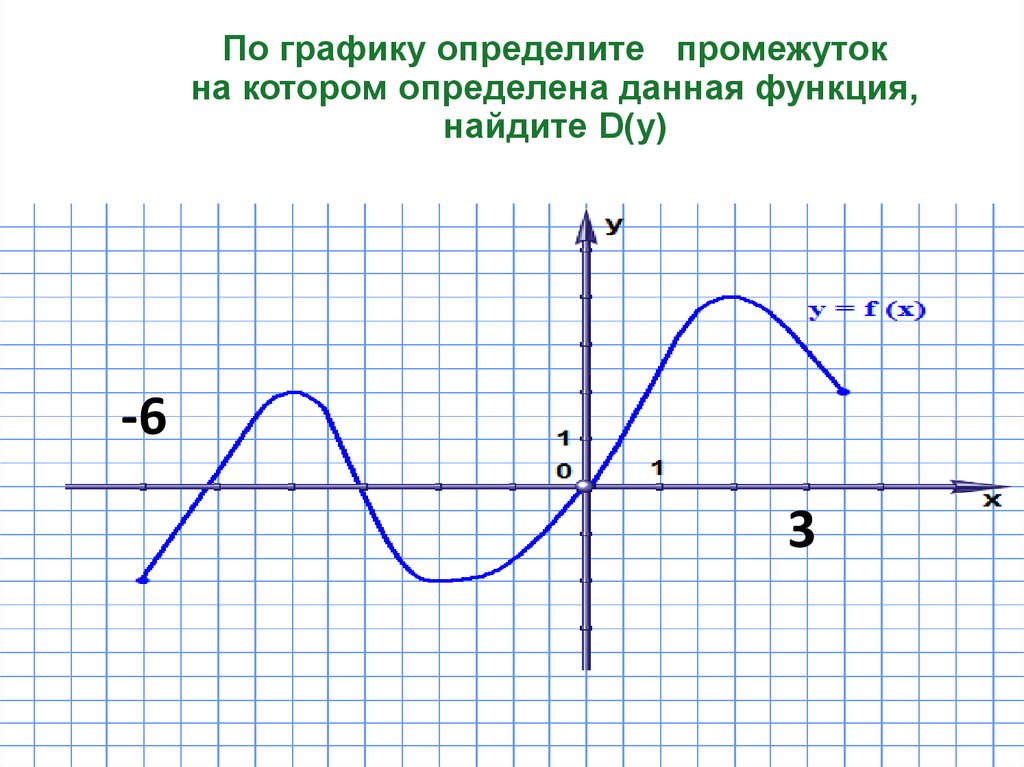
11. По графику определите промежуток на котором определена данная функция, найдите D(у)

-6
3

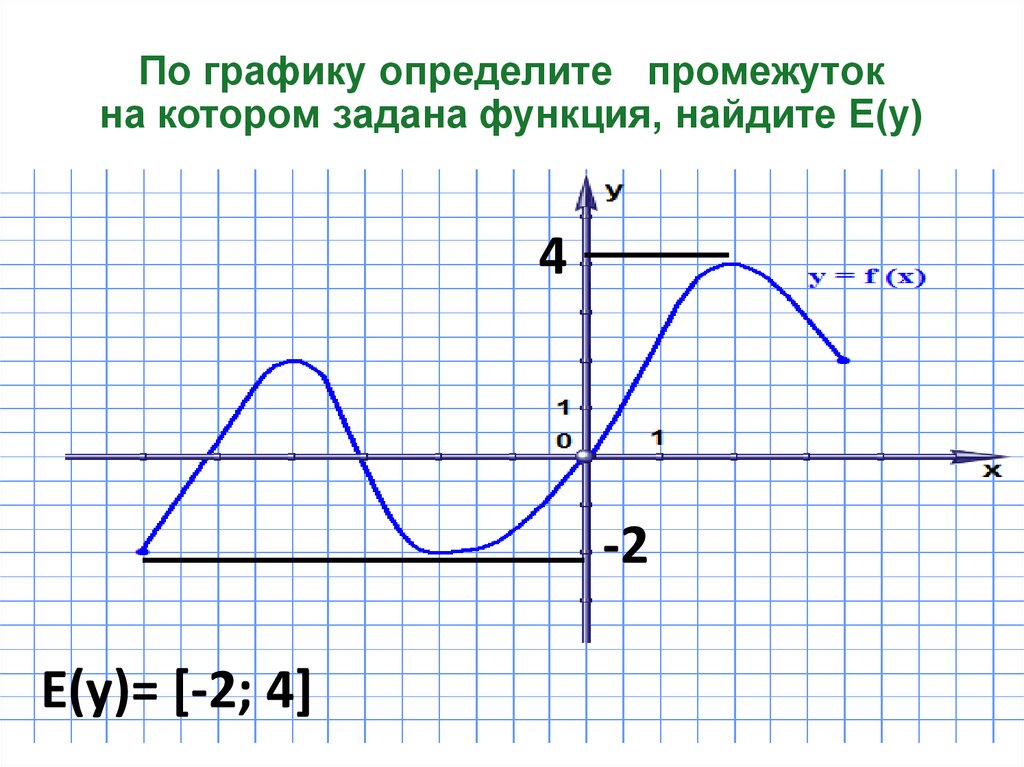
12. По графику определите промежуток на котором задана функция, найдите Е(у)

4
-2
Е(у)= [-2; 4]

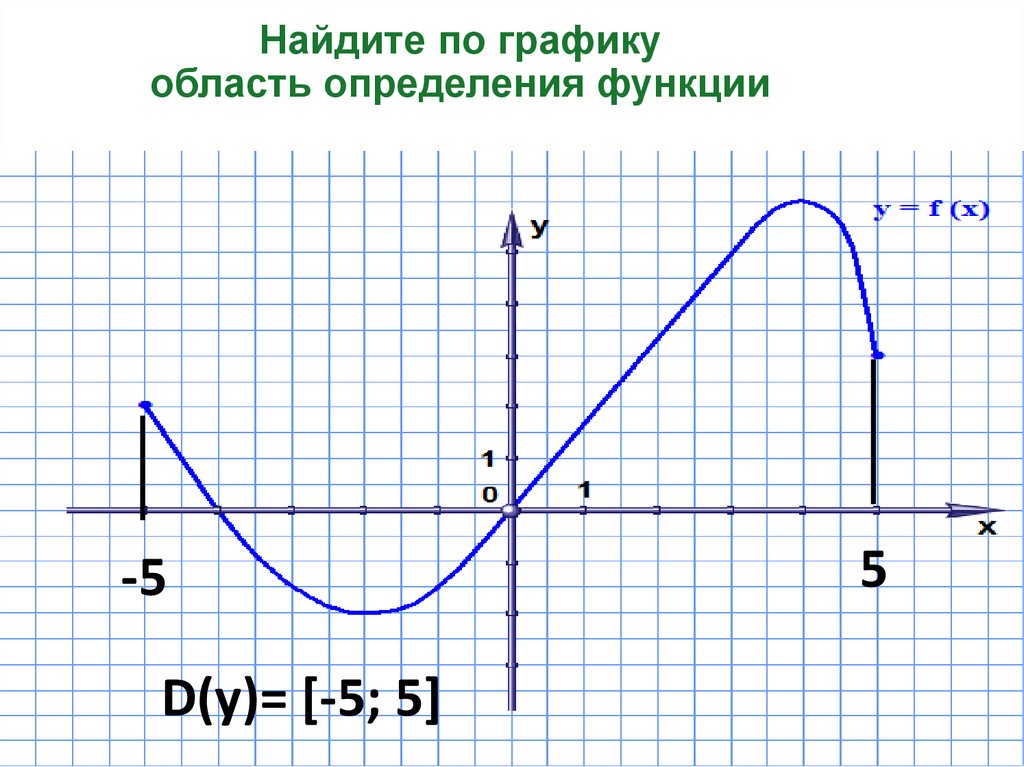
13. Найдите по графику область определения функции

-5
D(у)= [-5; 5]
5

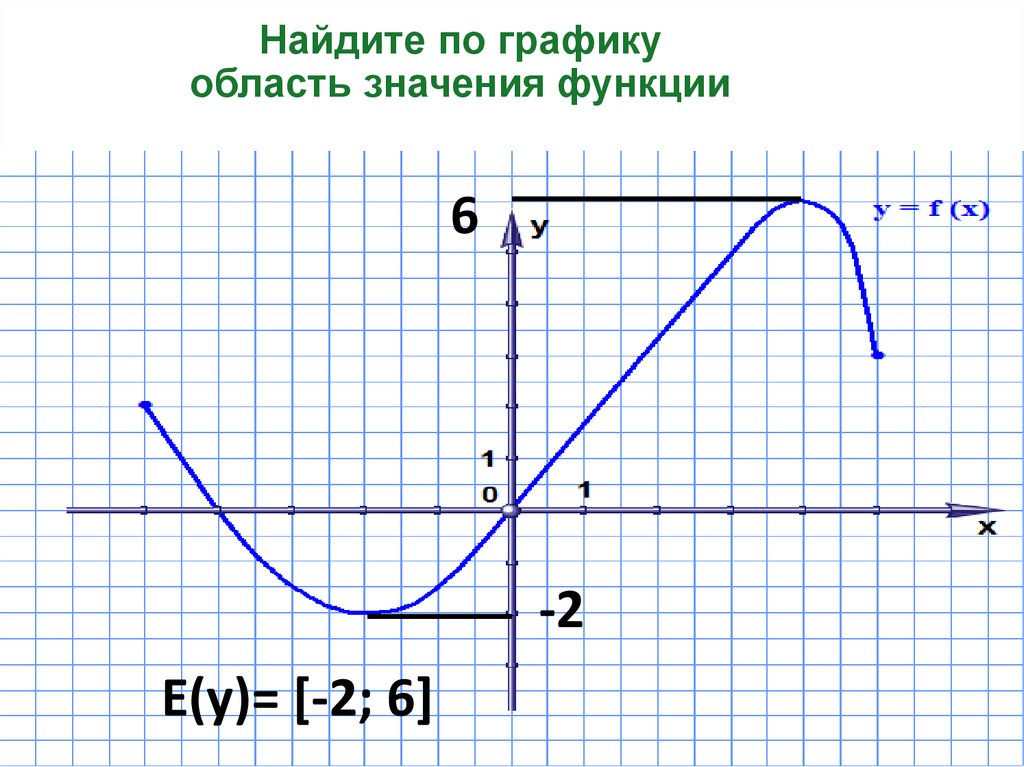
14. Найдите по графику область значения функции

6
-2
Е(у)= [-2; 6]

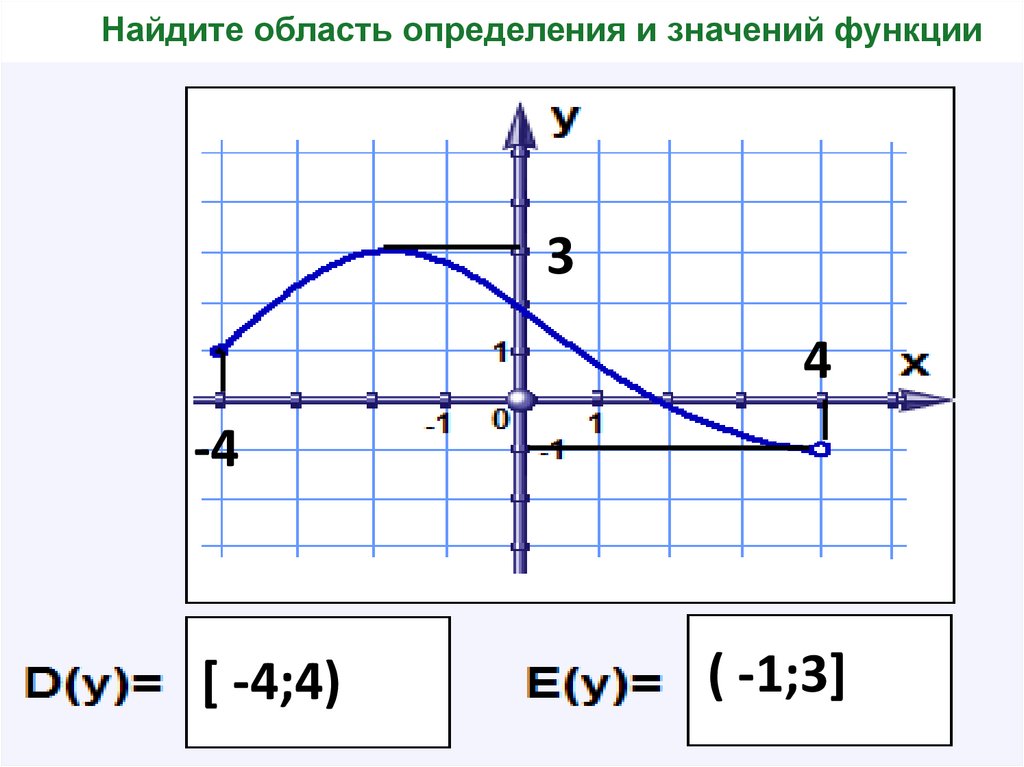
15. Найдите область определения и значений функции

3
4
-4
[ -4;4)
( -1;3]

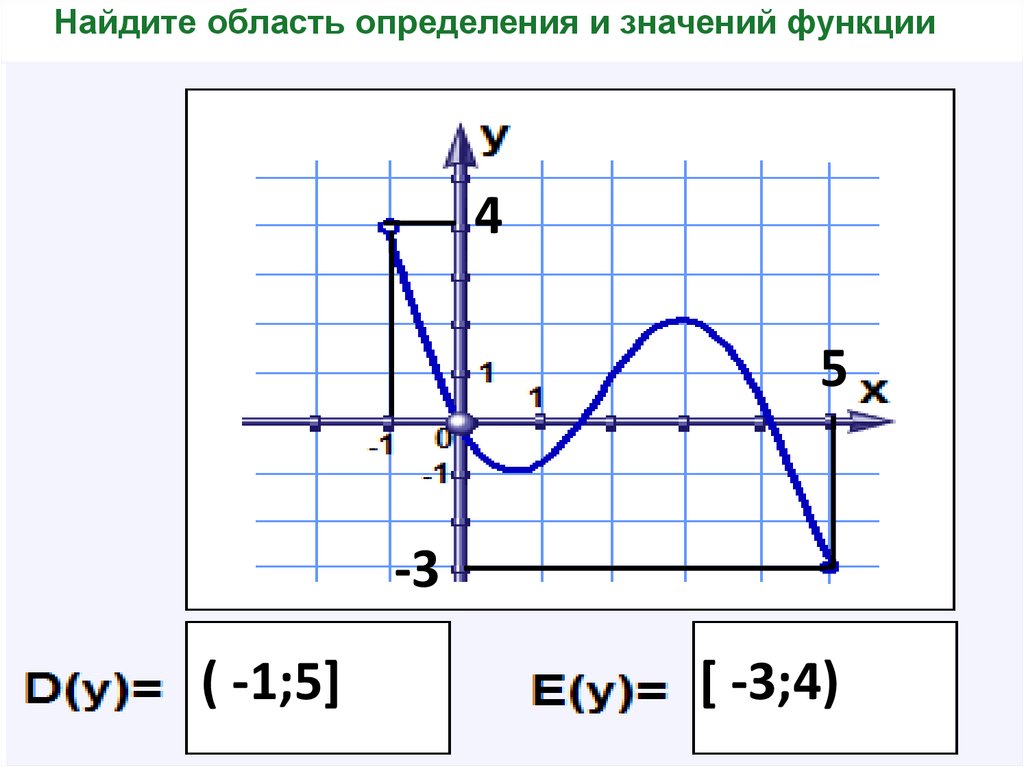
16. Найдите область определения и значений функции

4
5
-3
( -1;5]
[ -3;4)

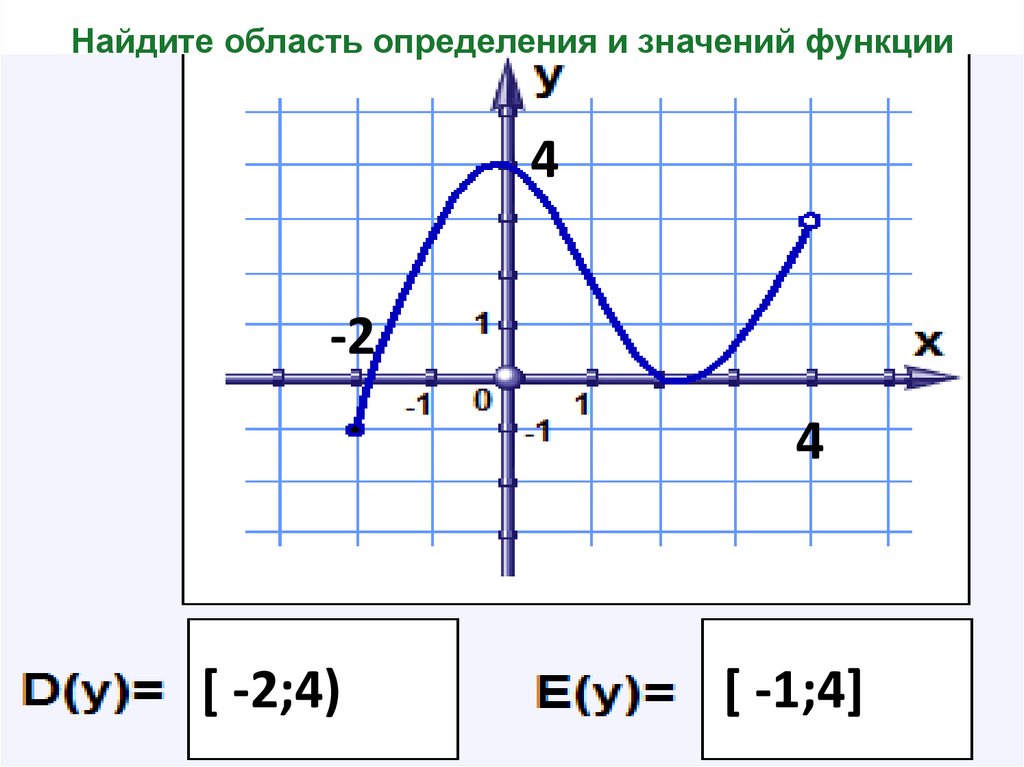
17. Найдите область определения и значений функции

4
-2
4
[ -2;4)
[ -1;4]

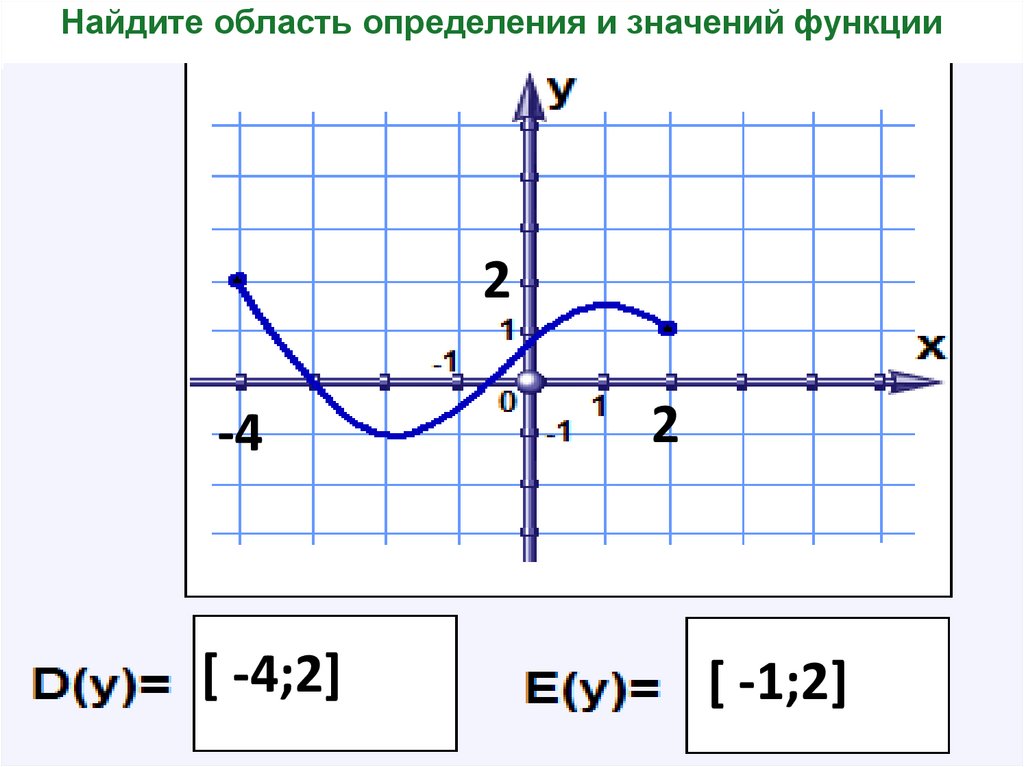
18. Найдите область определения и значений функции

2
-4
[ -4;2]
2
[ -1;2]

19.

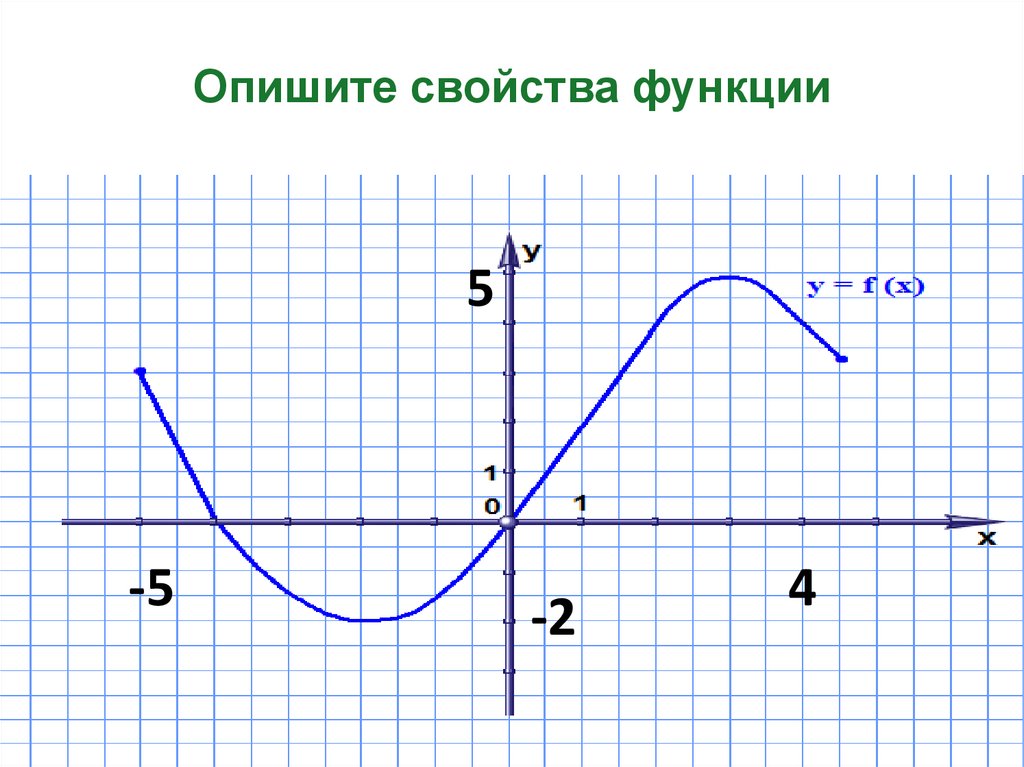
Опишите свойства функции
5
-5
-2
4