Готовимся к ГИА. Элементарные функции

1. Готовимся к ГИА Элементарные функции

(часть I)
Автор:
Драгунова С.А., учитель математики МБОУ СОШ № 19
г. Заполярный Мурманской области

2. ОГЛАВЛЕНИЕ

I. Функция, ее график и свойства
1. Определение функции
2. Свойства функции
II. Элементарные функции, их графики и свойства
1. Линейная функция
2. Функция прямой пропорциональности
3. Функция обратной пропорциональности
4. Функция y = x2
5. Функция y = аx2
6. Квадратичная функция
7. Функция y = x3
8. Функция y = kx3
9. Функция y = √x
10. Функция y =|x|
III. Задания для устной работы:
№ 1, № 2 , № 3, № 4, № 5, № 6, № 7, № 8.
Выход

3. Определение функции

Функциональная зависимость, или функция, - это такая
зависимость между двумя переменными, при которой каждому
значению независимой переменной соответствует единственное
значение зависимой переменной.
Независимую переменную называют аргументом. Значения
зависимой переменной называют значениями функции.
Графиком функции называют множество всех точек
координатной плоскости, абсциссы которых равны значениям
аргумента, а ординаты – соответствующим значениям функции.
М (х0; у0) – точка графика функции y = f(x), где х0 – аргумент
функции, у0 – значение функции.
y
у0
0
Оглавление
y = f(x)
М
х0
x

4. Свойства функции

1. Область определения:
D(у): х є [-5; 4].
y = f(x)
у>0
4
2. Множество значений функции:
Е(у): у є [-4; 4].
3. Нули функции:
у = 0 при х = - 3, х = 3.
4. Промежутки знакопостоянства:
у > 0 при х є (-3; 3);
у < 0 при х є [-5; -3) U (3; 4].
5. Промежутки монотонности:
функция возрастает при х є [-5; 0];
функция убывает при х є [0; 4].
Оглавление
-5
-5
-5
00
-3-3
-4
33 444
у<0

5. Линейная функция

Линейной функцией называется функция вида y = kx + b, где k,
b – числа, х – независимая переменная.
y
y = kx + b
b
(k > 0)
0
x
Графиком
линейной
функции является прямая,
k - угловой коэффициент,
b - показывает, в какой
точке график пересекает
ось ординат.
y
b
y = kx + b
(k < 0)
x
0
Если k = 0, то функция задается формулой y = b.
Графиком функции является прямая, параллельная оси абсцисс.
y
y=b
b
Оглавление
0
x
Свойства

6. Свойства линейной функции

y
y = kx + b
b
(k > 0)
x
0
y
b
y = kx + b
(k < 0)
0
x
1. Область
определения
D(у): х є R
2. Множество
значений
Е(у): у є R
3. Нули функции
точка пересечения графика с
осью Ох; у = 0, если х = - b/k
4. Промежутки
знакопостоянства
при k > 0
при k < 0
5. Промежутки
монотонности
Оглавление
у > 0, если х > - b/k;
у < 0, если х < - b/k
у > 0, если х < - b/k;
у < 0, если х > - b/k
если k > 0, то функция
возрастает; если k < 0, то
функция убывает

7. Функция прямой пропорциональности

Функцией прямой пропорциональности называется функция
вида y = kx , где k – число, х – независимая переменная.
y
y = kx
(k > 0)
0
Оглавление
x
Графиком
функции
прямой
пропорциональности
является
прямая,
проходящая
через
начало координат, k угловой коэффициент.
y
y = kx
(k < 0)
0
x
Свойства

8. Свойства функции прямой пропорциональности

1. Область
y = kx определения
y
(k > 0)
x
0
2. Множество
значений
3. Нули функции
y
y = kx
(k < 0)
0
Оглавление
x
D(у): х є R
Е(у): у є R
у = 0, если х = 0
4. Промежутки
знакопостоянства
при k > 0
при k < 0
у > 0, если х > 0; у < 0, если х < 0
у > 0, если х < 0; у < 0, если х > 0
5. Промежутки
монотонности
при k > 0 функция возрастает,
при k < 0 функция убывает

9. Функция обратной пропорциональности

Функцией обратной пропорциональности называется функция
вида y = k/x , где k ≠ 0, х – независимая переменная.
y
y = k/x
(k > 0)
0
Оглавление
x
y
График обратной
пропорциональности гипербола, состоящая
из двух ветвей.
y = k/x
(k < 0)
0
Свойства
x

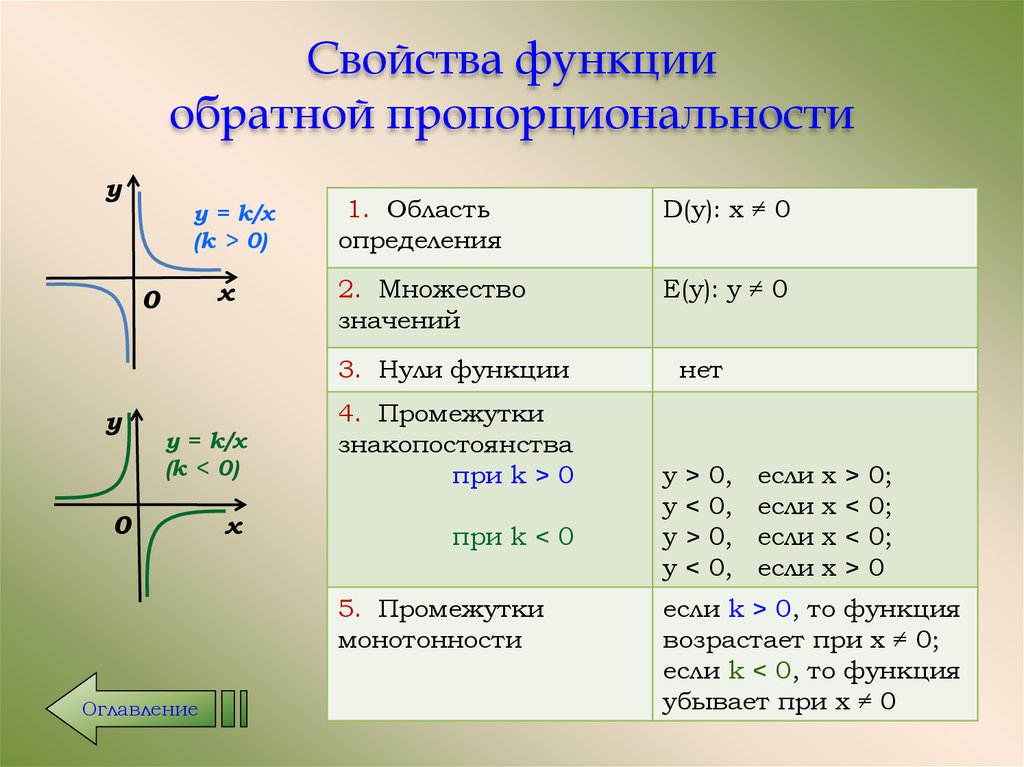
10. Свойства функции обратной пропорциональности

y
y = k/x
(k > 0)
x
0
1. Область
определения
D(у): х ≠ 0
2. Множество
значений
Е(у): у ≠ 0
3. Нули функции
y
y = k/x
(k < 0)
4. Промежутки
знакопостоянства
при k > 0
x
при k < 0
0
5. Промежутки
монотонности
Оглавление
нет
у
у
у
у
>
<
>
<
0,
0,
0,
0,
если
если
если
если
х
х
х
х
>
<
<
>
0;
0;
0;
0
если k > 0, то функция
возрастает при х ≠ 0;
если k < 0, то функция
убывает при х ≠ 0

11. Функция y = x2

График функции y = x2 – парабола, ветви которой
направлены вверх. Ось симметрии – ось ординат.
1. Область
определения
y
y = x2
0
x
2. Множество
Е(у): у ≥ 0
значений функции
3. Нули функции
у = 0, если х = 0
4. Промежутки
знакопостоянства
у > 0, если х ≠ 0
5. Промежутки
монотонности
Оглавление
D(у): х є R
при х ≥ 0 функция
возрастает;
при х ≤ 0 функция
убывает

12. Функция y = аx2

График y = аx2 (а ≠ 0) - парабола. Если а > 0, ветви параболы
направлены вверх, если а < 0, вниз. Ось симметрии – ось ординат.
y
аx2
y=
(а > 0)
0
x
1. Область
определения
2. Множество
а > 0: Е(у): у ≥ 0;
значений функции а < 0: Е(у): у ≤ 0
3. Нули функции
y
0
Оглавление
x
y = аx2
(а < 0)
D(у): х є R
у = 0, если х = 0
4. Промежутки
знакопостоянства
а > 0: у > 0, если х ≠ 0;
а < 0: у < 0, если х ≠ 0
5. Промежутки
монотонности
а > 0: при х ≥ 0 функция
возрастает; при х ≤ 0
функция убывает;
а < 0: при х ≤ 0 функция
возрастает; при х ≥ 0
функция убывает

13. Квадратичная функция

Функция вида y = аx2+bx+c, где а ≠ 0, b, c – числа, х –
независимая переменная, называется квадратичной функцией.
Квадратичная функция может быть задана формулой
y = а(x –m)2+n , где m = хв и n = ув .
y
y
аx2
y=
(а > 0)
0
ув
хв
x
График функции – парабола.
y = аx2
(а < 0) ув
0
хв x
Если а > 0, ветви параболы направлены вверх, если а < 0, вниз.
Ось симметрии – прямая, проходящая параллельно оси ординат
через вершину параболы. Координаты вершины:
Оглавление
х в=
в
2а
D
; ув= 4а
Свойства

14. Свойства квадратичной функции

аx2
y=
(а > 0)
y
y
y = аx2 у
в
(а < 0)
хв
0
ув
0
x
1. Область
определения
D(у): х є R
2. Множество
значений функции
а > 0: Е(у) = [ -D/(4a) ; +∞ )
а < 0: Е(у) = ( -∞ ; -D/(4a) ]
3. Нули функции
при D > 0
при D = 0
при D < 0
4. Промежутки
монотонности
Оглавление
два нуля:
один нуль:
нулей нет
хв x
b D
2a
- b/(2a)
а > 0: функция возрастает при х є [-b/(2a);+∞)
функция убывает при х є (-∞; -b/(2a)]
а < 0: функция возрастает при х є (-∞; -/(2a)]
функция убывает при х є [-b/(2a);+∞)
Свойства

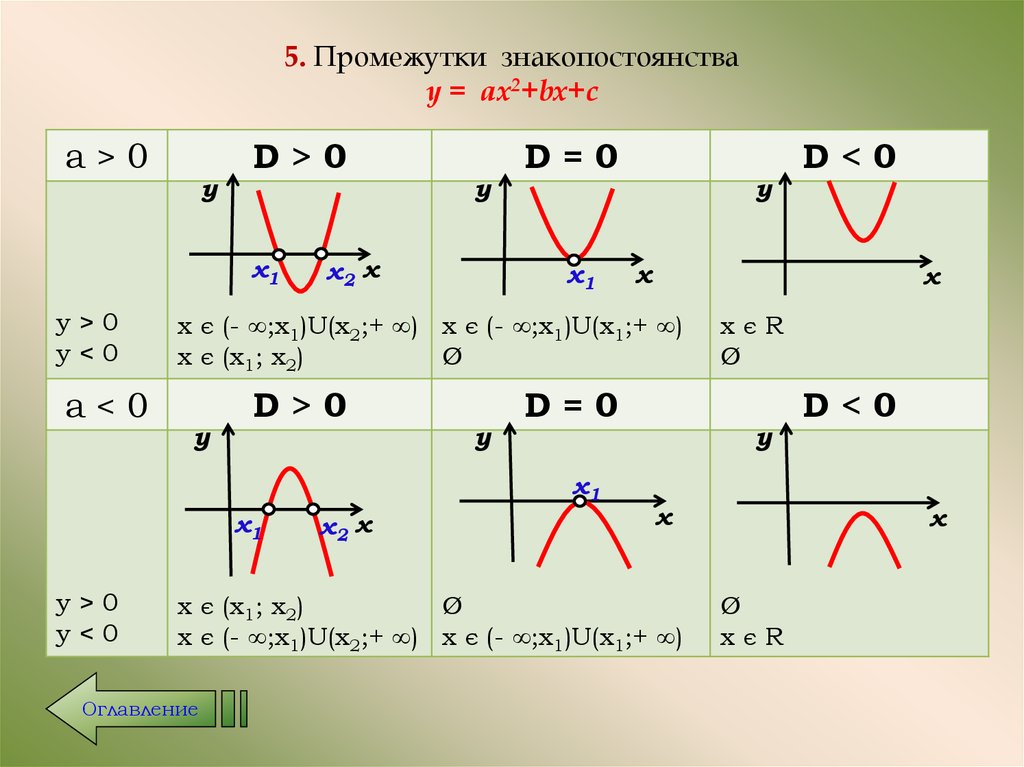
15. 5. Промежутки знакопостоянства у = ax2+bx+c

a>0
у
D>0
x1
y>0
y<0
a<0
у
x2 х
D=0
x1
х
х
х є (- ∞;x1)U(x2;+ ∞) х є (- ∞;x1)U(x1;+ ∞)
х є (x1; x2)
Ø
у
D>0
у
D=0
x1
x1
y>0
y<0
у
x2 х
хєR
Ø
у
х
х є (x1; x2)
Ø
х є (- ∞;x1)U(x2;+ ∞) х є (- ∞;x1)U(x1;+ ∞)
Оглавление
D<0
D<0
х
Ø
хєR

16. Функция y = x3

График y = x3 – кубическая парабола. График
симметричен относительно начала координат.
1. Область
определения
y
D(у): х є R
2. Множество
Е(у): у є R
значений функции
0
x
y = x3
Оглавление
3. Нули функции
у = 0, если х = 0
4. Промежутки
знакопостоянства
у > 0, если х > 0;
у < 0, если х < 0
5. Промежутки
монотонности
функция возрастает
при х є R

17. Функция y = kx3

График y = kx3 – кубическая парабола. График
симметричен относительно начала координат
y = kx3
(k > 0)
y
1. Область
определения
D(у): х є R
2. Множество
Е(у): у є R
значений функции
0
x
y = kx3
(k < 0)
Оглавление
3. Нули функции
4. Промежутки
знакопостоянства
при k > 0
при k < 0
5. Промежутки
монотонности
у = 0, если х = 0
у > 0,если х > 0; у < 0, если х < 0
у > 0,если х < 0; у < 0, если х > 0
если k > 0, то функция
возрастает, при х є R
если k < 0, то функция убывает,
при х є R

18. Функция y = √x

1. Область
определения
y
2. Множество
Е(у): у ≥ 0
значений функции
y = √x
0
Оглавление
D(у): х ≥ 0
x
3. Нули функции
у = 0, если х = 0
4. Промежутки
знакопостоянства
у > 0, если х > 0
5. Промежутки
монотонности
функция возрастает
при х ≥ 0

19. Функция y = |x|

График y = |x| симметричен относительно оси ординат.
1. Область
определения
y
y = |x|
0
Оглавление
x
D(у): х є R
2. Множество
Е(у): у ≥ 0
значений функции
3. Нули функции
у = 0, если х = 0
4. Промежутки
знакопостоянства
у > 0, если х ≠ 0
5. Промежутки
монотонности
при х ≥ 0 функция
возрастает;
при х ≤ 0 функция
убывает

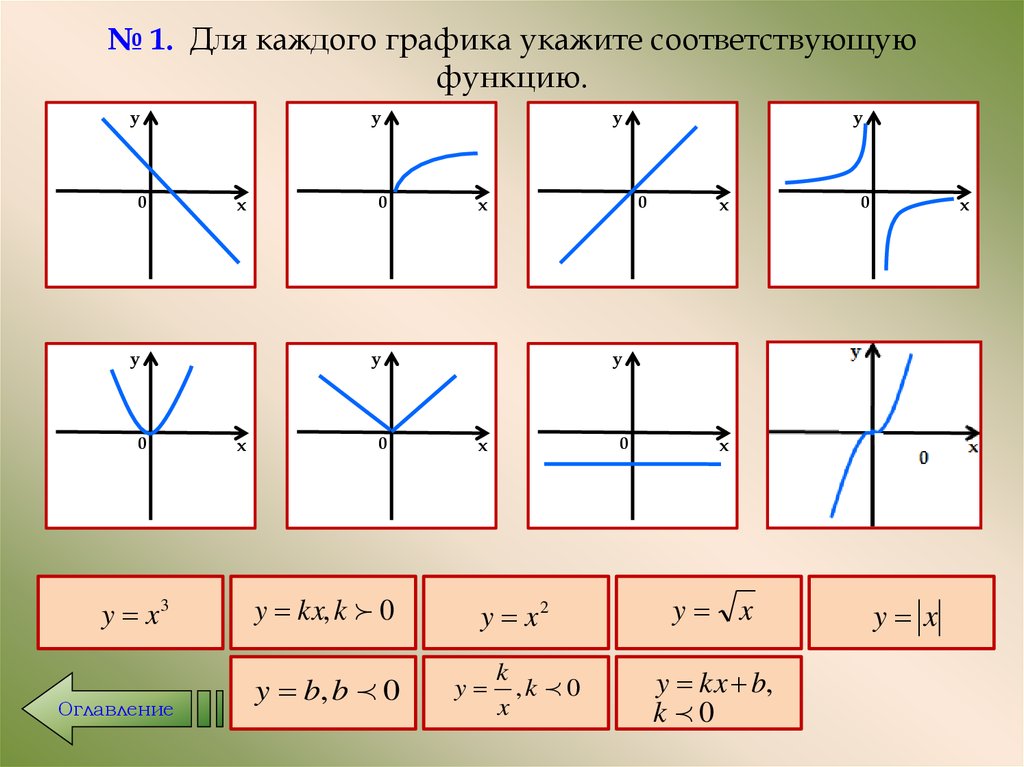
20. № 1. Для каждого графика укажите соответствующую функцию.

y
0
y
x
y
0
y x3
Оглавление
0
y
0
x
y
x
0
y kx, k 0
y b, b 0
y
x
0
x
y
0
x
y x2
y
k
,k 0
x
x
y x
y kx b,
k 0
y x

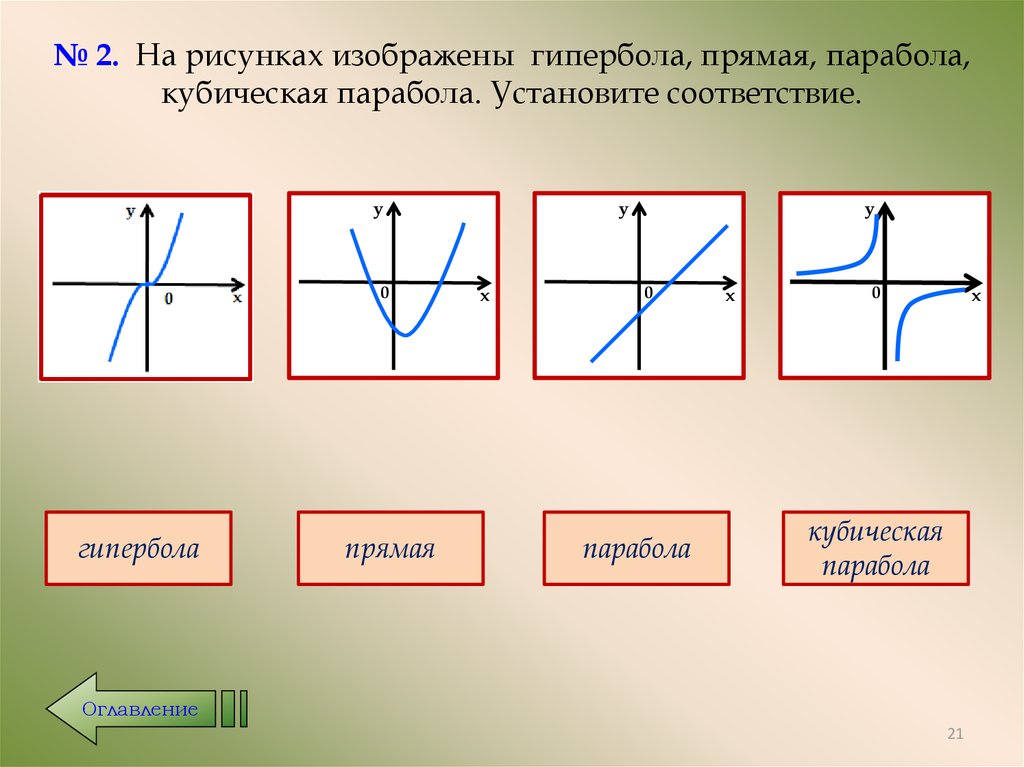
21. № 2. На рисунках изображены гипербола, прямая, парабола, кубическая парабола. Установите соответствие.

y
0
гипербола
прямая
y
x
y
0
парабола
x
0
x
кубическая
парабола
Оглавление
21

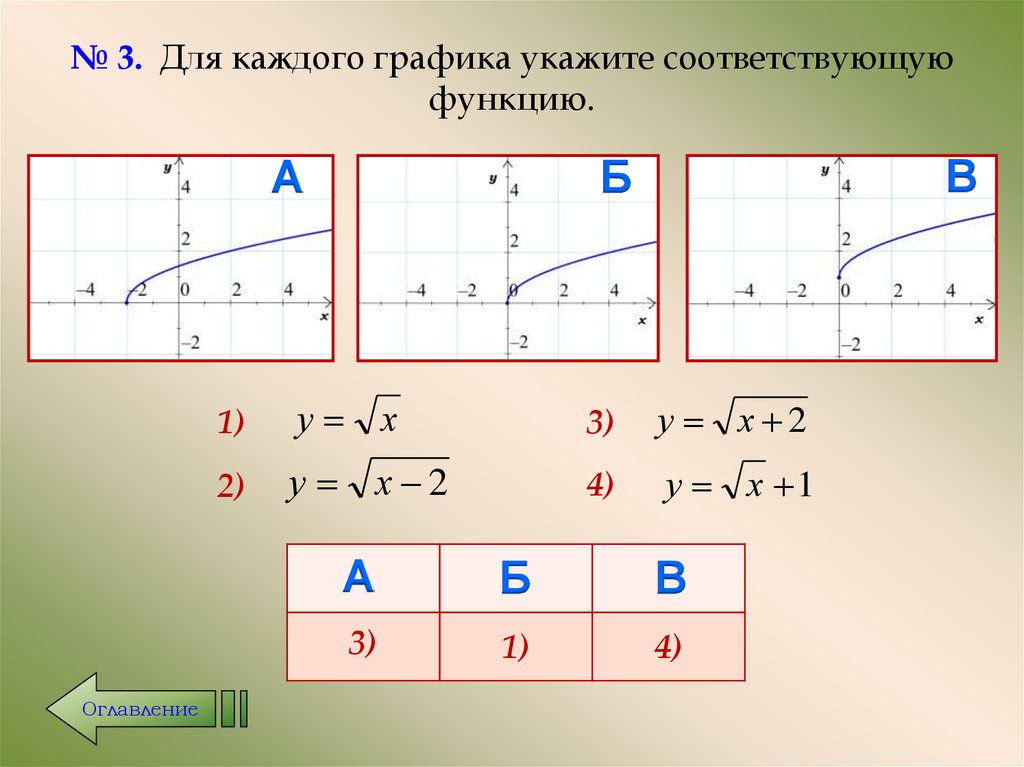
22. № 3. Для каждого графика укажите соответствующую функцию.

А
Оглавление
В
Б
1)
у х
3)
у х 2
2)
у х 2
4)
у х 1
А
Б
В
3)
1)
4)

23. № 4. Для каждого графика укажите соответствующую функцию.

А
1)
2)
Оглавление
Б
у = х³ - 1
у = (х – 1)³
3)
4)
В
у = х³ + 1
у = х³
А
Б
В
4)
1)
2)

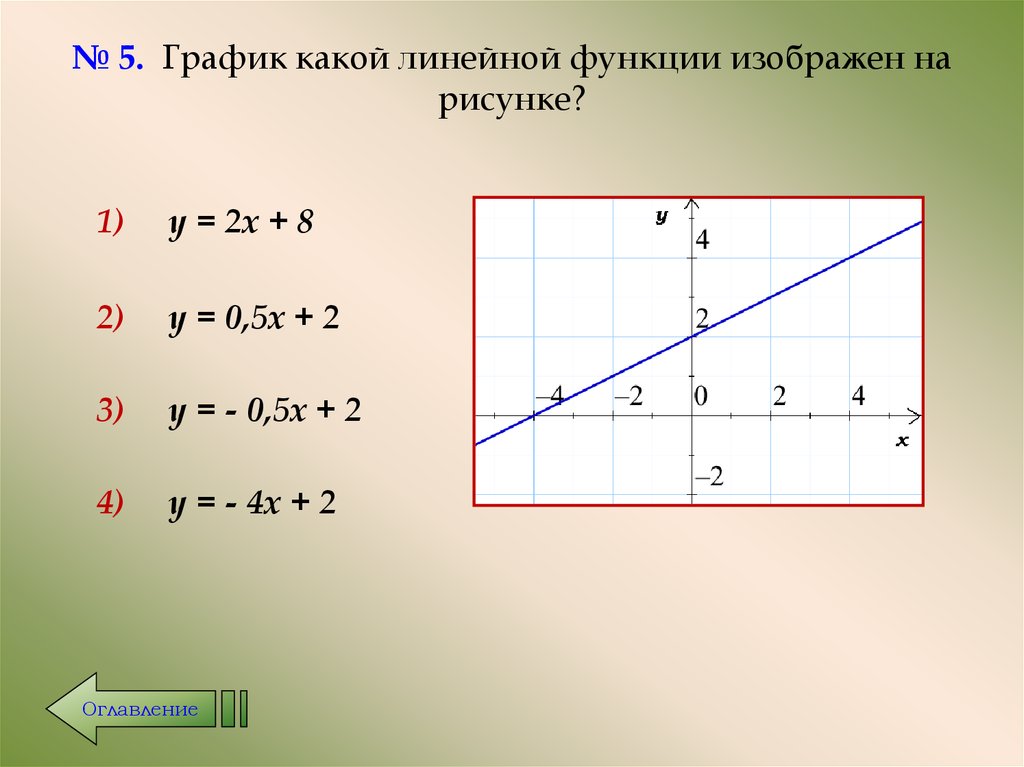
24. № 5. График какой линейной функции изображен на рисунке?

1)
у = 2х + 8
2)
у = 0,5х + 2
3)
у = - 0,5х + 2
4)
у = - 4х + 2
Оглавление

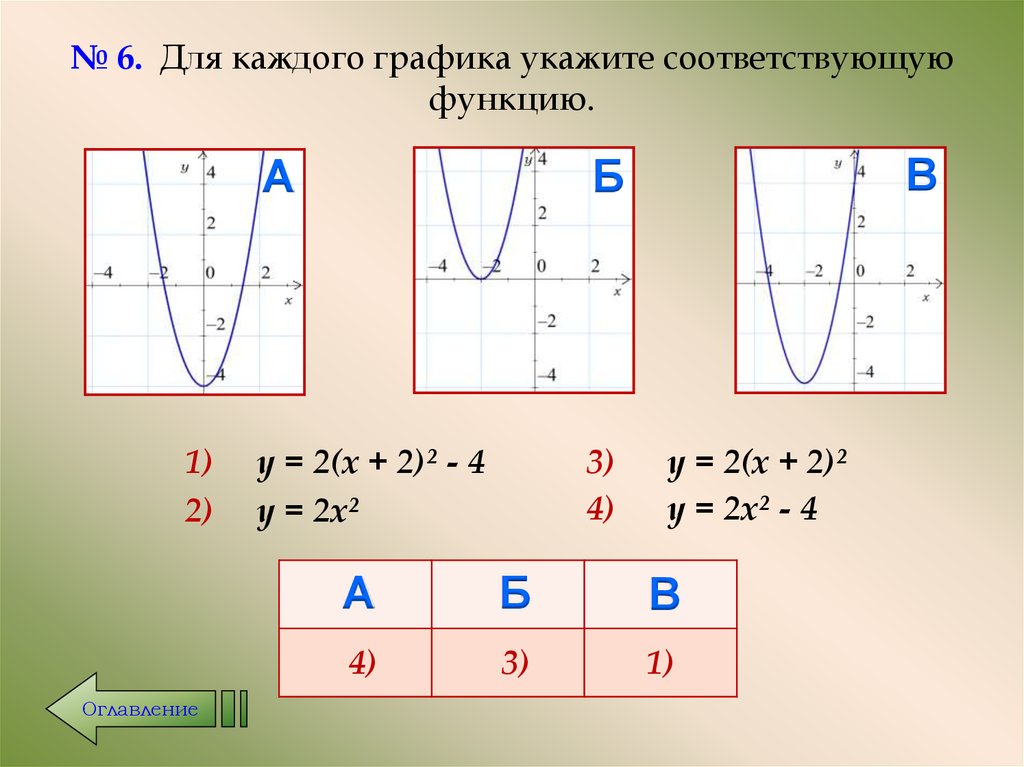
25. № 6. Для каждого графика укажите соответствующую функцию.

1)
2)
Оглавление
А
Б
у = 2(х + 2)² - 4
у = 2х²
3)
4)
В
у = 2(х + 2)²
у = 2х² - 4
А
Б
В
4)
3)
1)

26. № 7. На рисунке изображен график функции у = f (х), заданной на промежутке [- 2; 3,5]. Из приведенных ниже утверждений выберите верное.

1) f(x) > 0 при -1 < х < 3;
2) функция у = f(x)
возрастает на [0 ; 2];
3) f(0) = 1;
4) наименьшее значение
функции равно -1.
Оглавление

27.

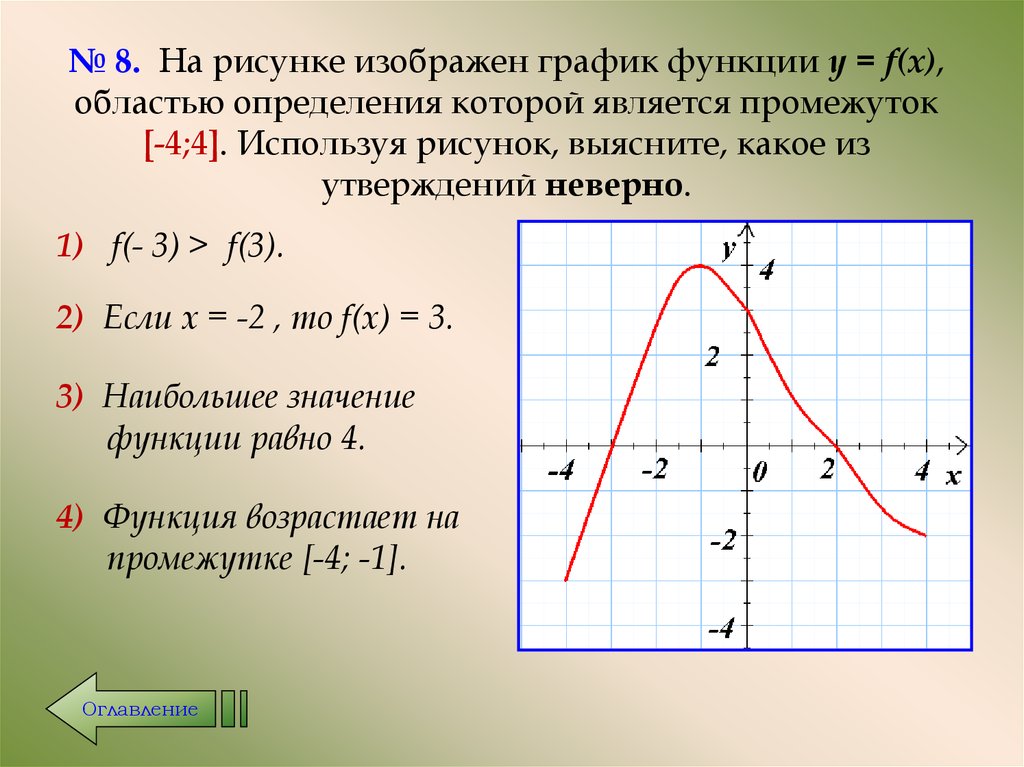
№ 8. На рисунке изображен график функции у = f(x),
областью определения которой является промежуток
[-4;4]. Используя рисунок, выясните, какое из
утверждений неверно.
1) f(- 3) > f(3).
2) Если х = -2 , то f(x) = 3.
3) Наибольшее значение
функции равно 4.
4) Функция возрастает на
промежутке [-4; -1].
Оглавление

28.

Литература
1. Кузнецова Л.В. и др. «Государственная аттестация
выпускников 9 классов в новой форме».
Математика. 2011/ ФИПИ. – М.: Интеллект-Центр,
2011.
2. Неискашова Е.В. «Алгебра: 50 типовых вариантов
экзаменационных работ для подготовки к ГИА: 9-й
класс. / Е.В. Неискашова. - М.: АСТ: Астрель, 2009.
Оглавление