Similar presentations:
Функция и её свойства
1. Функция и её свойства
9 классУрок повторения и обобщения
изученного материала
Церетели Н.К.
2. Содержание
Цели урока
Определение
Виды функций
Свойства функций
Задание 1
Задание 2
Тест
3. Цели урока
Закрепление свойств функцииРазвитие умений исследования
графиков функции
Выполнение упражнений и построение
графиков функций
4. Определение
Функция – зависимость одной переменнойот другой, причем для любых значений х
соответствует единственное значение
функции y.
График функции – множество всех точек
координатной плоскости, абсциссы которых
равны значениям аргумента, а ординаты
соответствующим значениям функции.
5. Виды функций
Линейная
Прямая пропорциональность
Обратная пропорциональность
Квадратичная
Квадратный корень
Модуль
Другие функции
6. Свойства функций
1. Область определения функции2. Множество значений функции
3. Монотонность
4. Четность
5. Ограниченность
6. Наибольшее, наименьшее значение
7. Точки экстремума
8. Выпуклость
9. Пересечение с осями координат
10. Промежутки знакопостоянства
7. Задание 1
• Изобразите схематически графики функцийy 2x 1
y x
y 3x
y x
4
y
x
y x
2
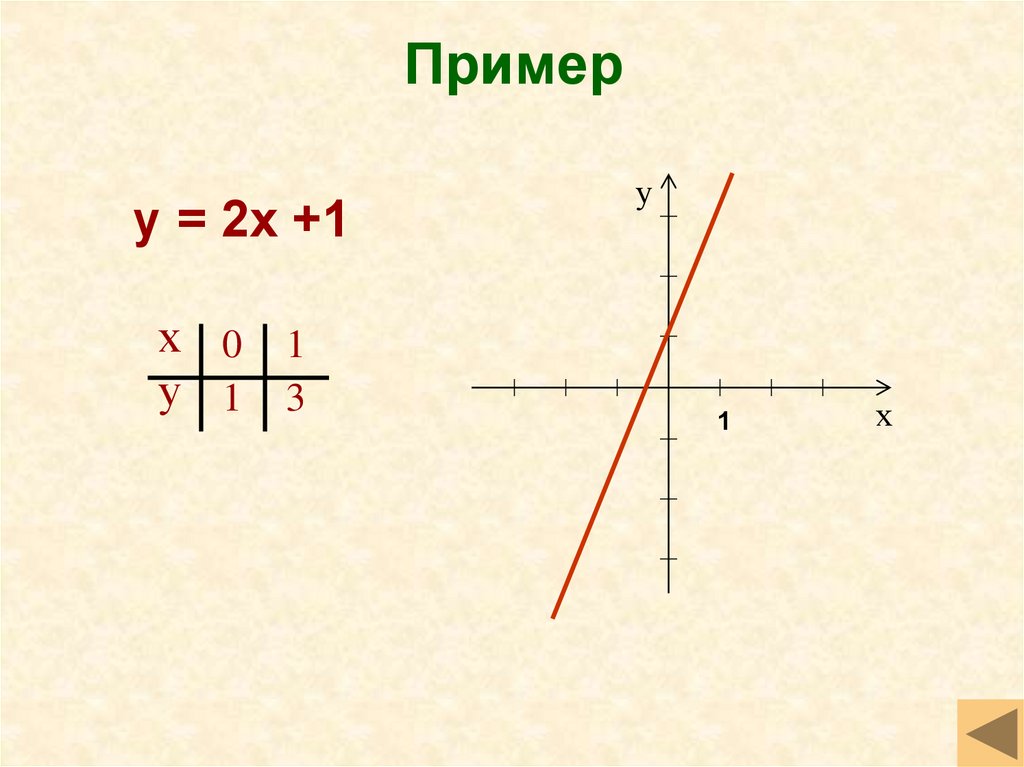
8. Пример
у = 2х +1х 0 1
у 1 3
у
1
х
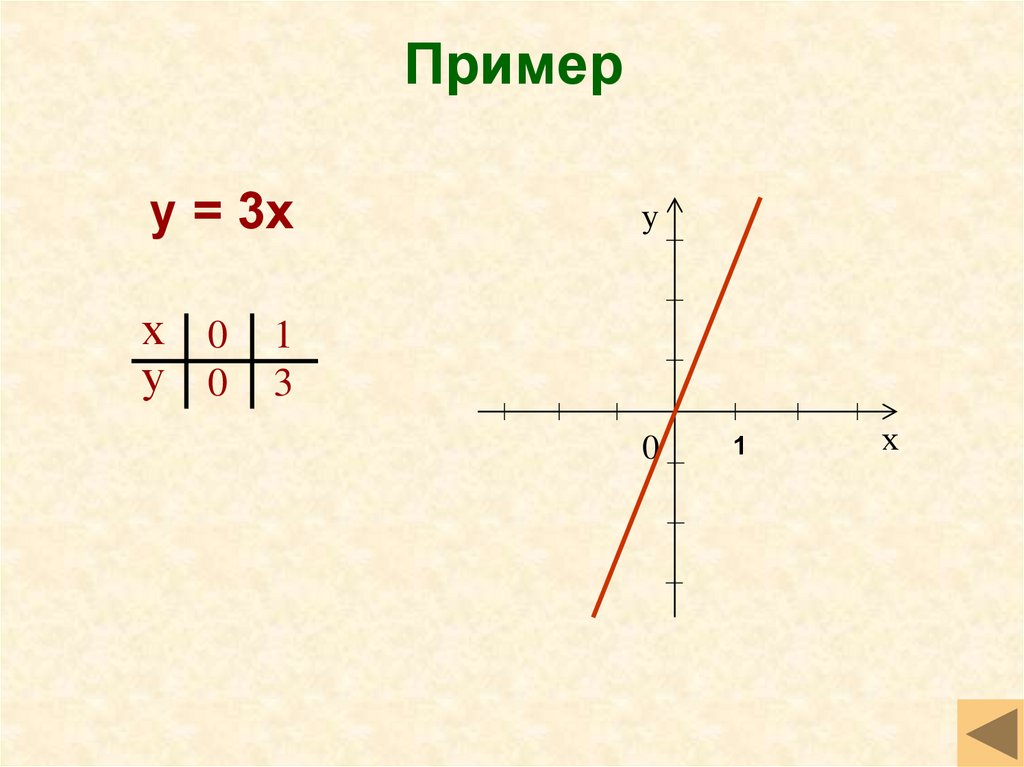
9. Пример
у = 3хх 0
у 0
у
1
3
0
1
х
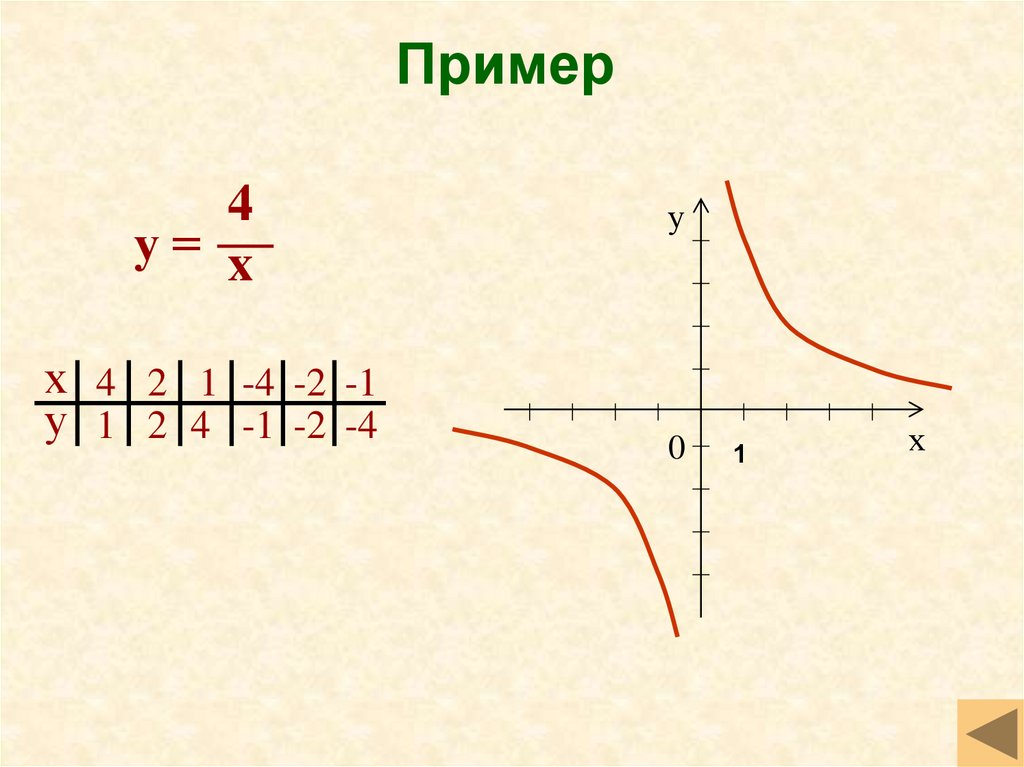
10. Пример
4у= x
х 4 2 1 -4 -2 -1
у 1 2 4 -1 -2 -4
у
0
1
х
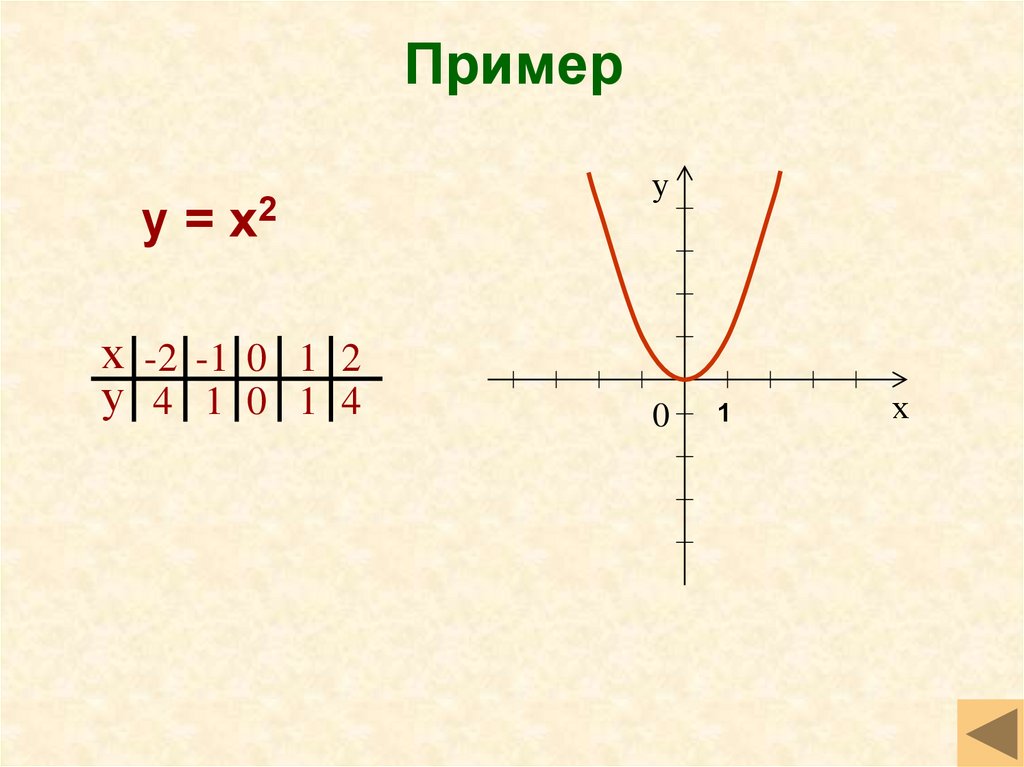
11. Пример
у = х2х -2 -1 0 1 2
у 4 1 0 1 4
у
0
1
х
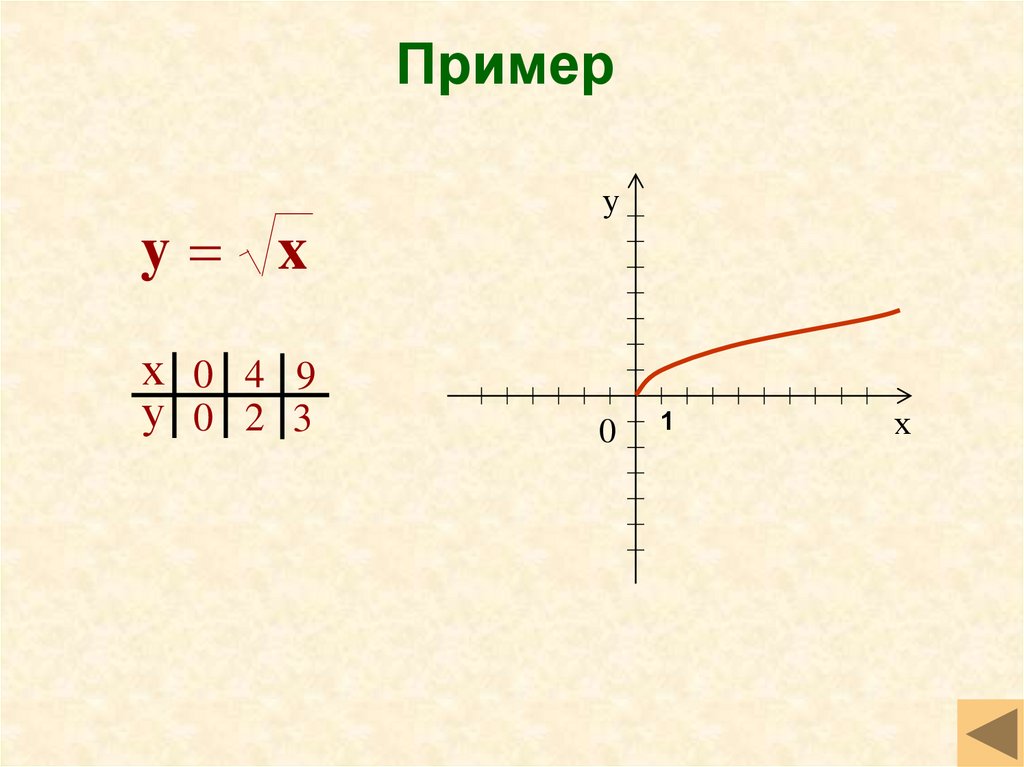
12. Пример
y xх 0 4 9
у 0 2 3
у
0
1
х
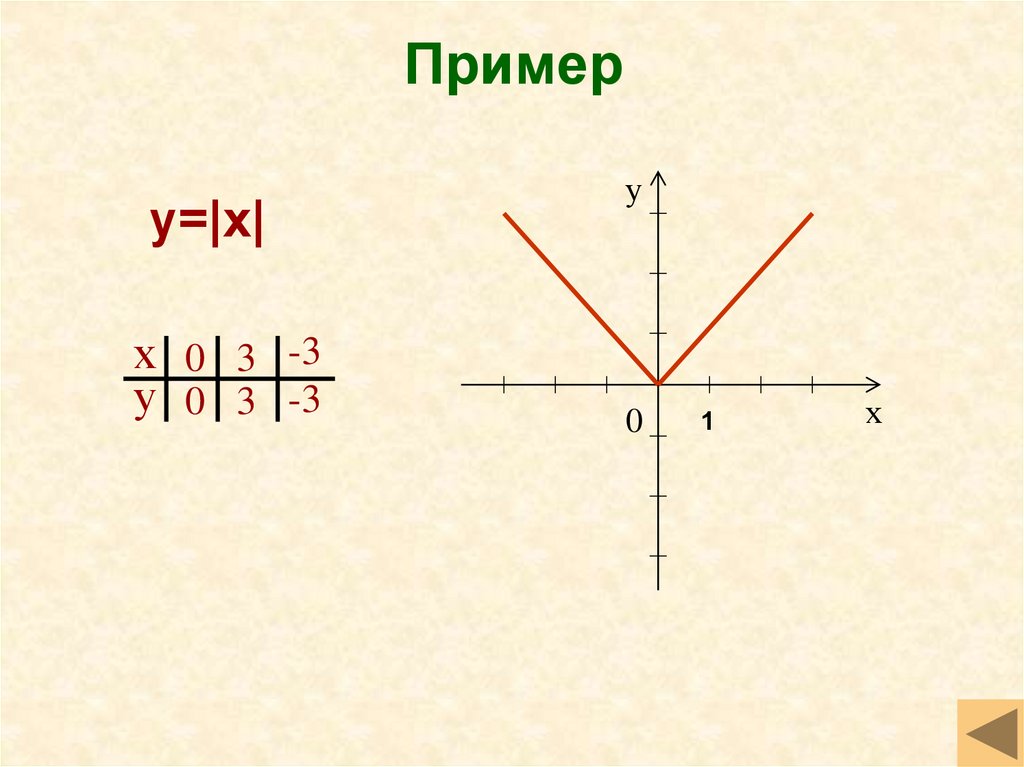
13. Пример
y=|x|х 0 3 -3
у 0 3 -3
у
0
1
х
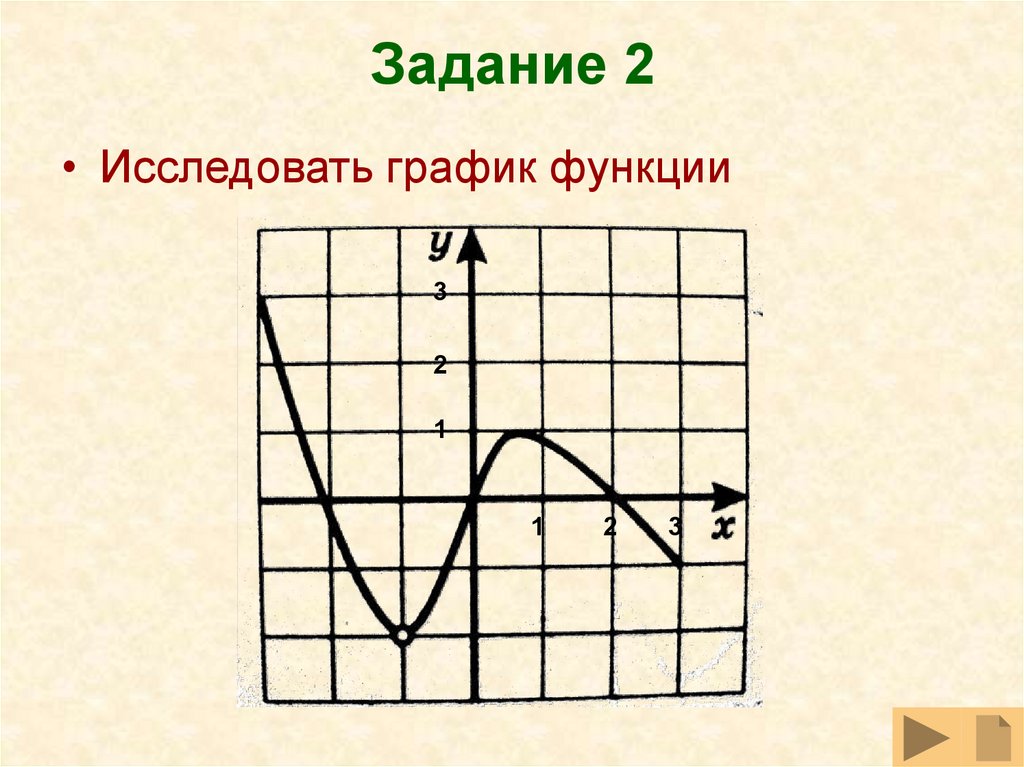
14. Задание 2
• Исследовать график функции3
2
1
1
2
3
15. Тест
1. Найдите область определения функцииy 4 2x
а)
а)
б)
б)
в)
в)
г)
г)
x 2
x 2
x 2
x 2
1
x 1
x 2
2
x 2
x 2
а)
а)
б)
б)
в)
в)
г)
г)
x 2
x 2
x 2
x 2
1
x 1
x 2
x 22
x 2
16.
2. Исследуйте на ограниченность функциюy 2x 3x 1
2
а) ограничена сверху
б) ограничена снизу
в) ограничена снизу и сверху
г) не ограничена ни снизу, ни сверху
17.
3. Среди заданных функций укажите1) yвозрастающие
2x
2
1)
y 2x
2)
y 5x 1
3)
y 3 x
4)
y x
а) 2, 4
б) 1, 2, 4
2
2)
y 5x 1
3)
y 3 x
4)
y x
в) 3
г) 1, 2
18.
1) y убывающиеx
4. Среди заданных функций укажите
2
2)
y 2x 3
1)
y x2
3)
y 4 x
2)
y 2x 3
4)
y x
3)
y 4 x
4)
y x
а) 1, 3
б) 3
в) 3, 4
г) 1
19.
1)y 2x
2)
y x
3)
y 5x
4)
y x
2
5. Среди заданных функций укажите четные
1)
y 2x
2)
y x
3)
y 5x
а) 1, 3 y x
4)
б) 1, 2
2
в) 3, 4
г) 1, 4
20. 6. Среди заданных функций укажите нечетные
1)y 2x
2
6. Среди заданных функций укажите нечетные
y 2x 2
3)
3
y
x
y 5x
3
y
x
y 5x
4)
y x
2)
1)
2)
3)
4)
а) 1, 3y x
б) 2, 4
в) 2, 3
г) 3, 4
21. 7. Найдите множество значений функций
y 4 xа)
а)
б)
б)
в)
в)
г)
г)
;4;4
;4;4
0;4
0;4
4;
4;
а)
а)
б)
б)
в)
в)
г)
г)
2
;4;4
;4;4
0;4
0;4
4;4;
22. Верно
23. Не верно
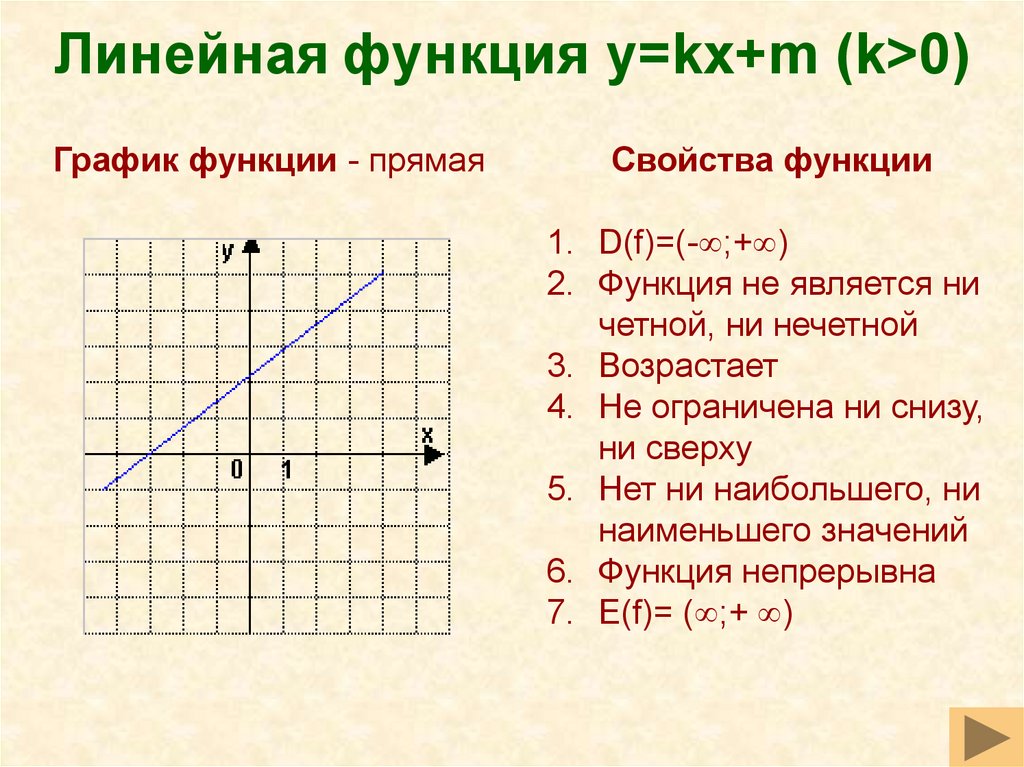
24. Линейная функция y=kх+m (k>0)
Линейная функция y=kх+m (k>0)График функции - прямая
1
Свойства функции
1. D(f)=(- ;+ )
2. Функция не является ни
четной, ни нечетной
3. Возрастает
4. Не ограничена ни снизу,
ни сверху
5. Нет ни наибольшего, ни
наименьшего значений
6. Функция непрерывна
7. Е(f)= ( ;+ )
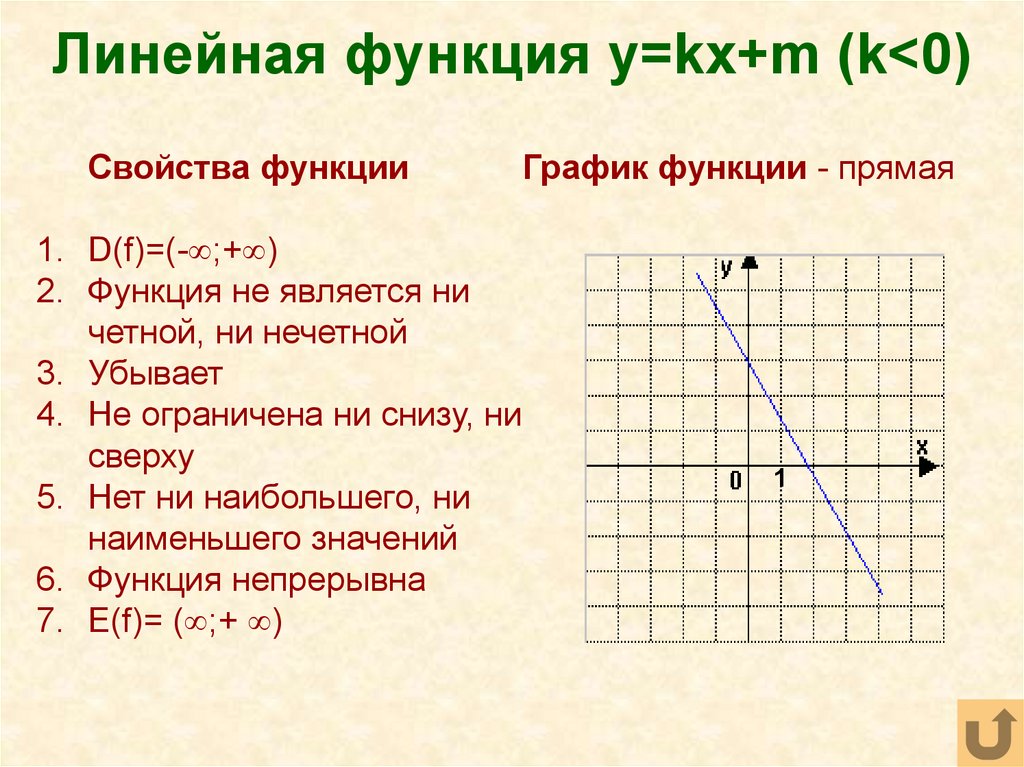
25. Линейная функция y=kx+m (k<0)
Линейная функция y=kx+m (k<0)Свойства функции
1. D(f)=(- ;+ )
2. Функция не является ни
четной, ни нечетной
3. Убывает
4. Не ограничена ни снизу, ни
сверху
5. Нет ни наибольшего, ни
наименьшего значений
6. Функция непрерывна
7. Е(f)= ( ;+ )
График функции - прямая
1
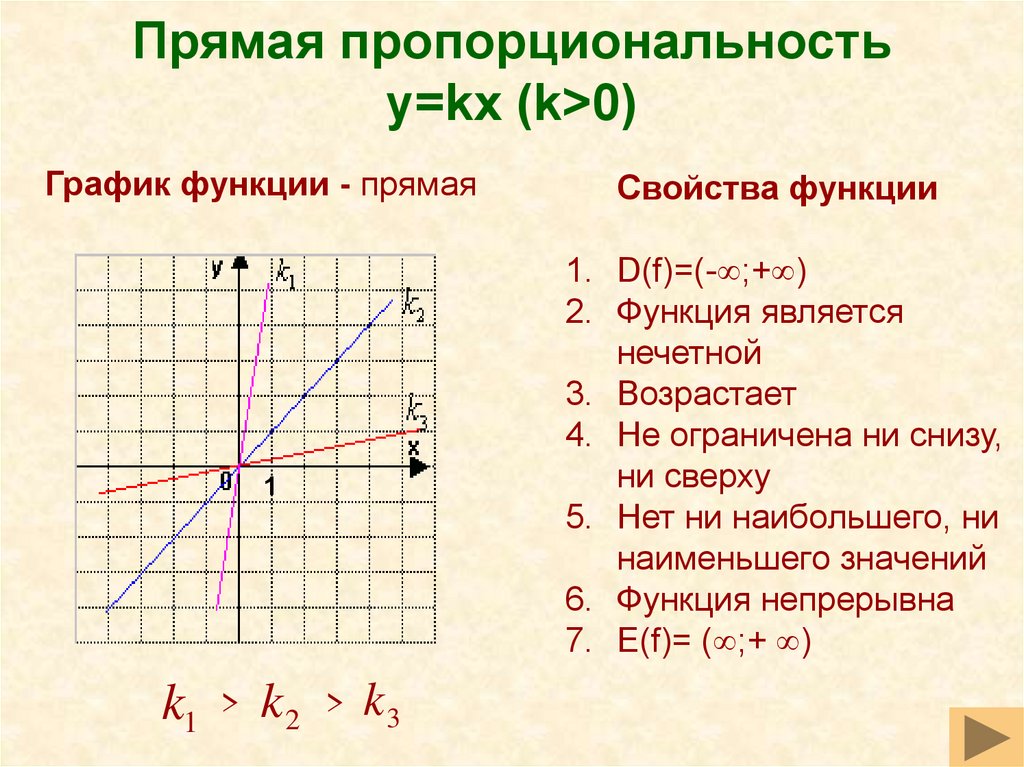
26. Прямая пропорциональность y=kx (k>0)
Прямая пропорциональностьy=kx (k>0)
График функции - прямая
1. D(f)=(- ;+ )
2. Функция является
нечетной
3. Возрастает
4. Не ограничена ни снизу,
ни сверху
5. Нет ни наибольшего, ни
наименьшего значений
6. Функция непрерывна
7. Е(f)= ( ;+ )
1
k1
>
k2
Свойства функции
>
k3
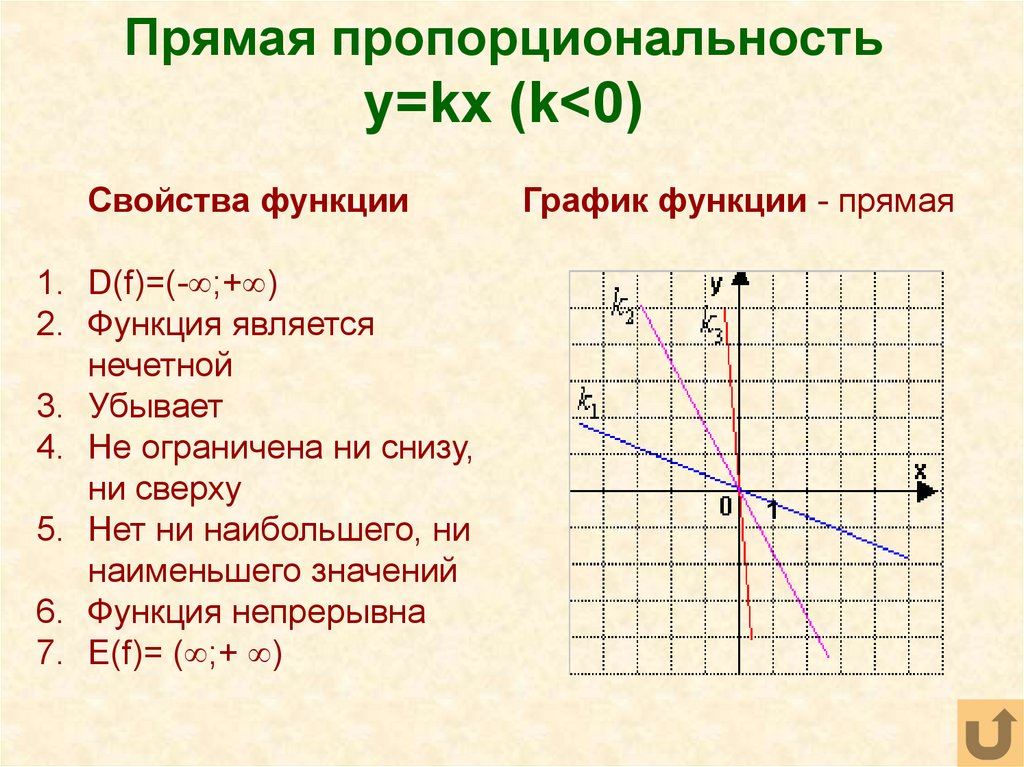
27. Прямая пропорциональность y=kx (k<0)
Прямая пропорциональностьy=kx (k<0)
Свойства функции
1. D(f)=(- ;+ )
2. Функция является
нечетной
3. Убывает
4. Не ограничена ни снизу,
ни сверху
5. Нет ни наибольшего, ни
наименьшего значений
6. Функция непрерывна
7. Е(f)= ( ;+ )
График функции - прямая
1
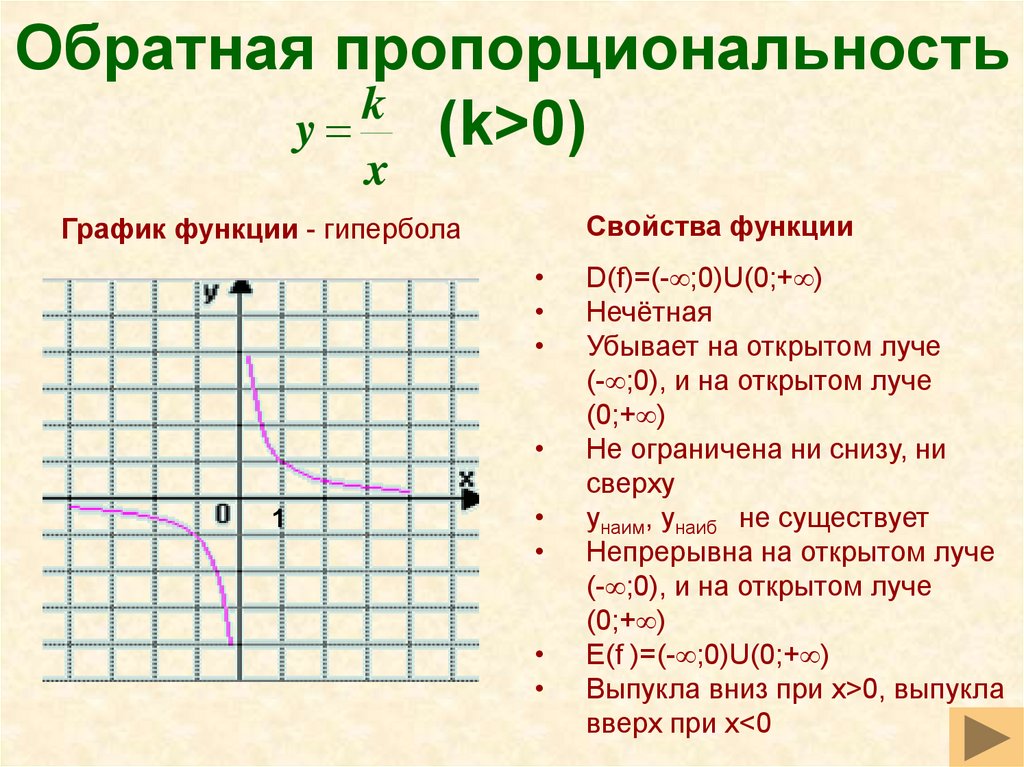
28. Обратная пропорциональность (k>0)
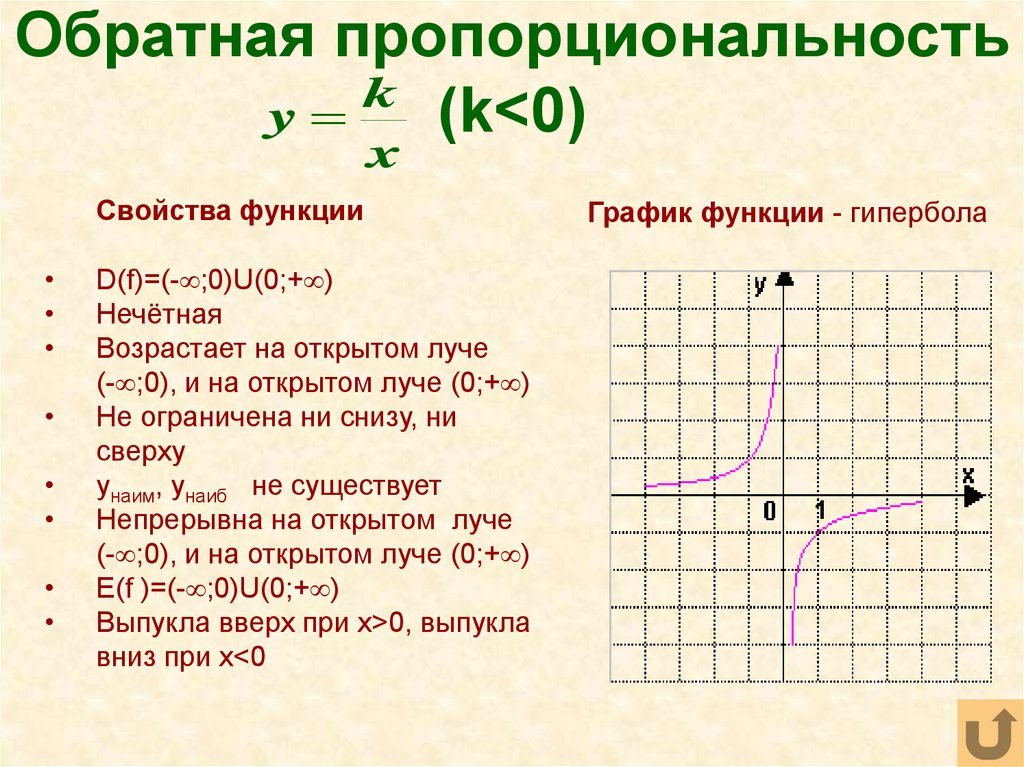
Обратная пропорциональностьk
y
(k>0)
x
Свойства функции
График функции - гипербола
1
D(f)=(- ;0)U(0;+ )
Нечётная
Убывает на открытом луче
(- ;0), и на открытом луче
(0;+ )
Не ограничена ни снизу, ни
сверху
yнаим, yнаиб не существует
Непрерывна на открытом луче
(- ;0), и на открытом луче
(0;+ )
E(f )=(- ;0)U(0;+ )
Выпукла вниз при x>0, выпукла
вверх при x<0
29. Обратная пропорциональность (k<0)
Обратная пропорциональностьk
y
(k<0)
x
Свойства функции
D(f)=(- ;0)U(0;+ )
Нечётная
Возрастает на открытом луче
(- ;0), и на открытом луче (0;+ )
Не ограничена ни снизу, ни
сверху
yнаим, yнаиб не существует
Непрерывна на открытом луче
(- ;0), и на открытом луче (0;+ )
E(f )=(- ;0)U(0;+ )
Выпукла вверх при x>0, выпукла
вниз при x<0
График функции - гипербола
1
30. Квадратичная функция y=kx2 (k>0)
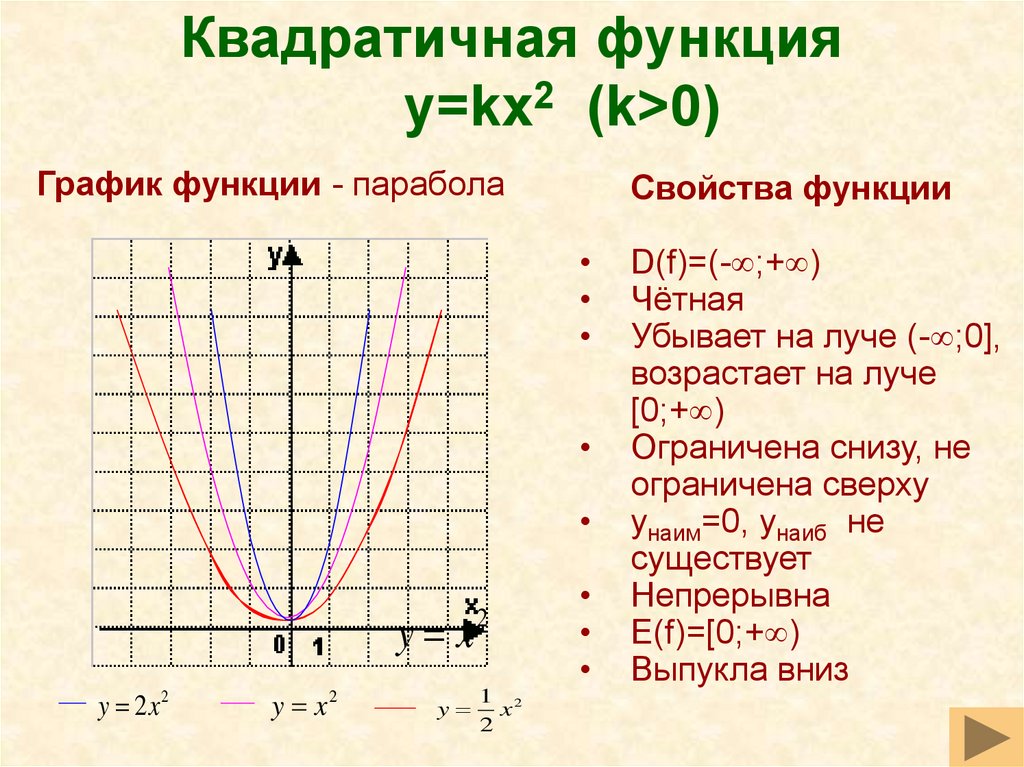
Квадратичная функцияy=kx2 (k>0)
График функции - парабола
Свойства функции
y x2
y 2x 2
y x2
y
1 2
x
2
D(f)=(- ;+ )
Чётная
Убывает на луче (- ;0],
возрастает на луче
[0;+ )
Ограничена снизу, не
ограничена сверху
yнаим=0, yнаиб не
существует
Непрерывна
E(f)=[0;+ )
Выпукла вниз
31. Квадратичная функция y=kx2 (k<0)
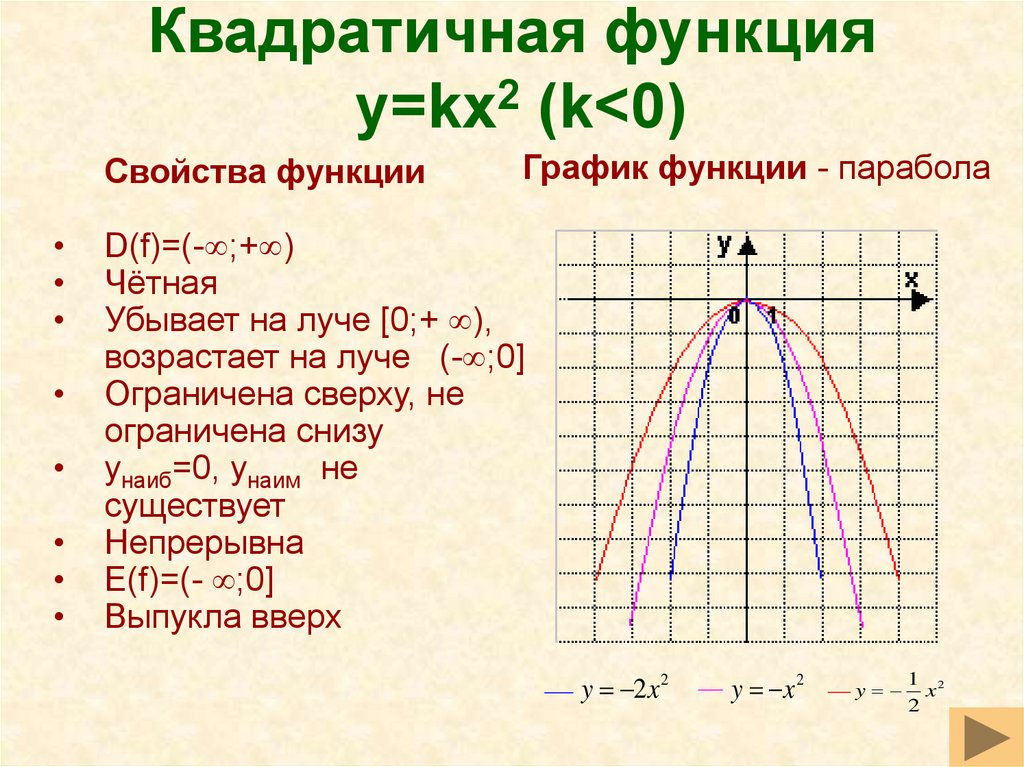
Квадратичная функцияy=kx2 (k<0)
Свойства функции
График функции - парабола
D(f)=(- ;+ )
Чётная
Убывает на луче [0;+ ),
возрастает на луче (- ;0]
Ограничена сверху, не
ограничена снизу
yнаиб=0, yнаим не
существует
Непрерывна
E(f)=(- ;0]
Выпукла вверх
y 2x 2
y x2
y
1 2
x
2
32. Квадратичная функция y=ax2+bx+c (a>0)
Квадратичная функцияy=ax2+bx+c (a>0)
График функции - парабола
Свойства функции
1. D(f)=(- ;+ )
2. Убывает на луче (- ; в ],
2а
возрастает на луче [ 2ва; + )
3. Ограничена снизу, не
ограничена сверху
4. yнаим= y0 , yнаиб – не существует
5. Непрерывна
1
6. E(f)=[y0 ;+ )
7. Выпукла вниз
33. Квадратичная функция y=ax2+bx+c (a<0)
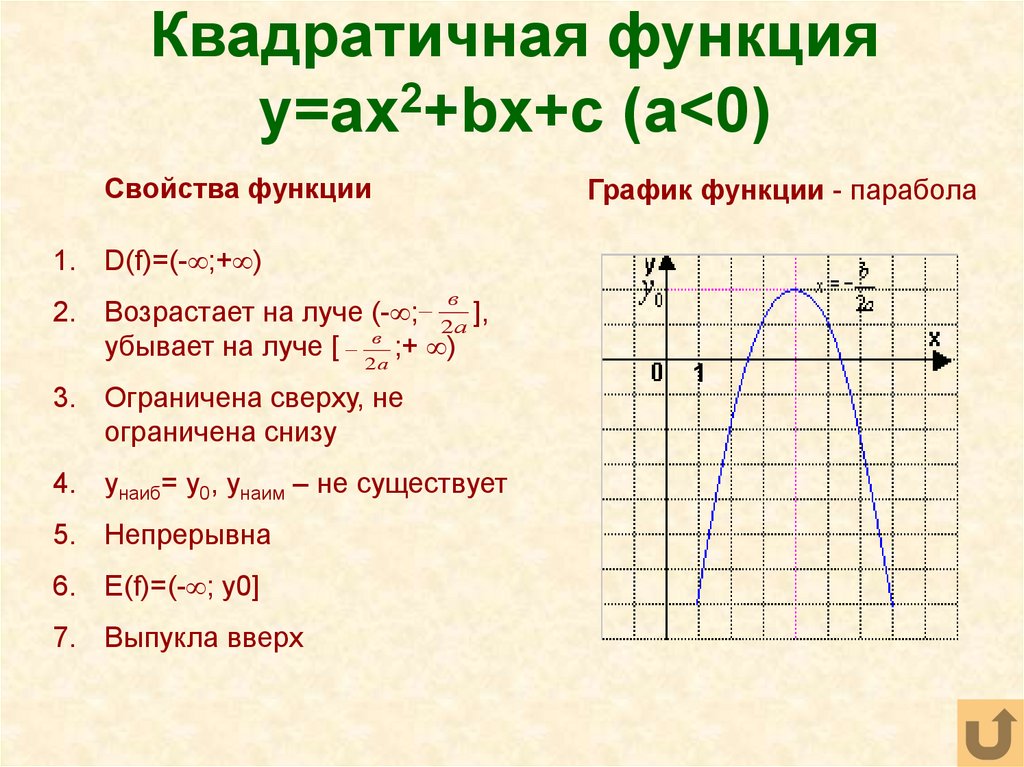
Квадратичная функцияy=ax2+bx+c (a<0)
Свойства функции
График функции - парабола
1. D(f)=(- ;+ )
в
2. Возрастает на луче (- ; 2а ],
убывает на луче [ 2ва ;+ )
3. Ограничена сверху, не
ограничена снизу
4. yнаиб= y0, yнаим – не существует
5. Непрерывна
6. E(f)=(- ; y0]
7. Выпукла вверх
1
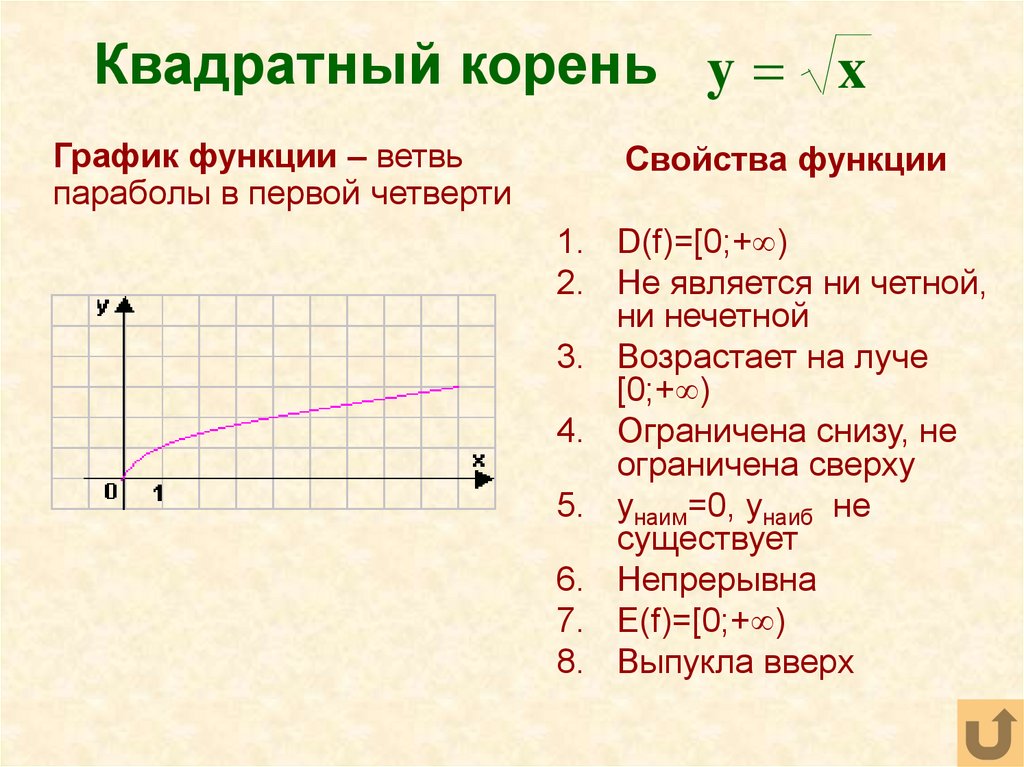
34. Квадратный корень
y xГрафик функции – ветвь
параболы в первой четверти
Свойства функции
1. D(f)=[0;+ )
2. Не является ни четной,
ни нечетной
3. Возрастает на луче
[0;+ )
4. Ограничена снизу, не
ограничена сверху
5. yнаим=0, yнаиб не
существует
6. Непрерывна
7. E(f)=[0;+ )
8. Выпукла вверх
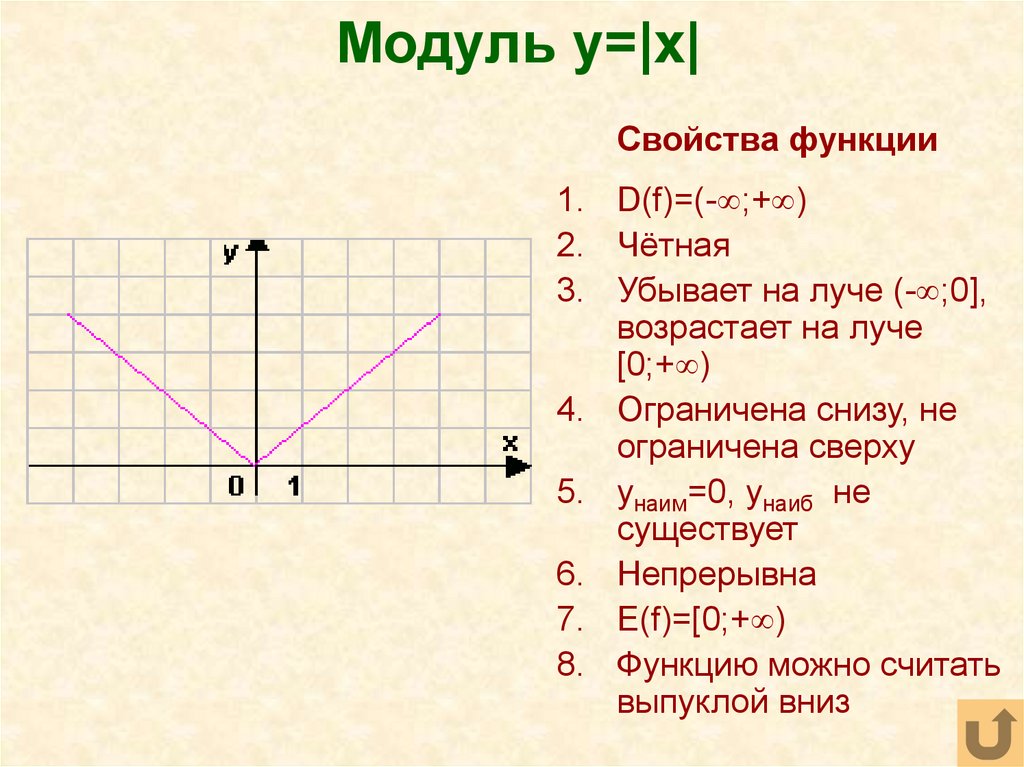
35. Модуль y=|x|
Свойства функции1. D(f)=(- ;+ )
2. Чётная
3. Убывает на луче (- ;0],
возрастает на луче
[0;+ )
4. Ограничена снизу, не
ограничена сверху
5. yнаим=0, yнаиб не
существует
6. Непрерывна
7. E(f)=[0;+ )
8. Функцию можно считать
выпуклой вниз
36. Функция y=x2n+1 (n N)
Свойства функции1.
2.
3.
4.
5.
6.
7.
8.
D(f)=(- ;+ )
Нечётная
Возрастает
Не ограничена ни снизу, ни
сверху
yнаим, yнаиб не существует
Непрерывна
E(f )=(- ;+ )
Выпукла вверх при x<0
Выпукла вниз при x>0
График функции кубическая парабола
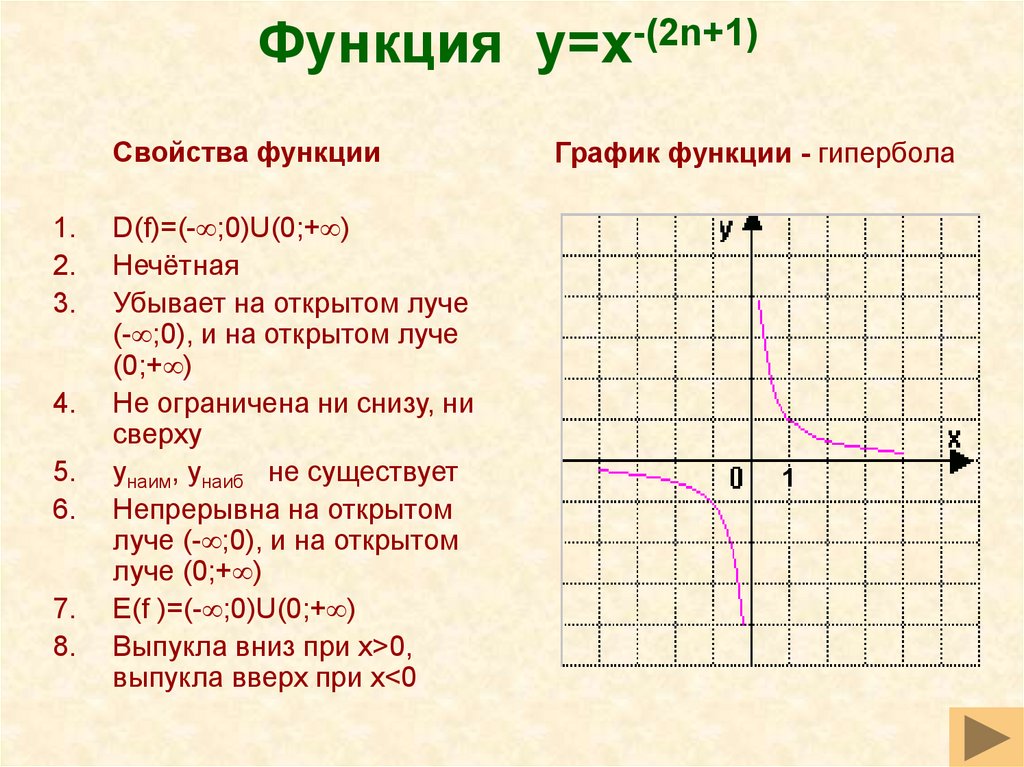
37. Функция y=x-(2n+1)
Свойства функции1.
2.
3.
4.
5.
6.
7.
8.
D(f)=(- ;0)U(0;+ )
Нечётная
Убывает на открытом луче
(- ;0), и на открытом луче
(0;+ )
Не ограничена ни снизу, ни
сверху
yнаим, yнаиб не существует
Непрерывна на открытом
луче (- ;0), и на открытом
луче (0;+ )
E(f )=(- ;0)U(0;+ )
Выпукла вниз при x>0,
выпукла вверх при x<0
График функции - гипербола
1
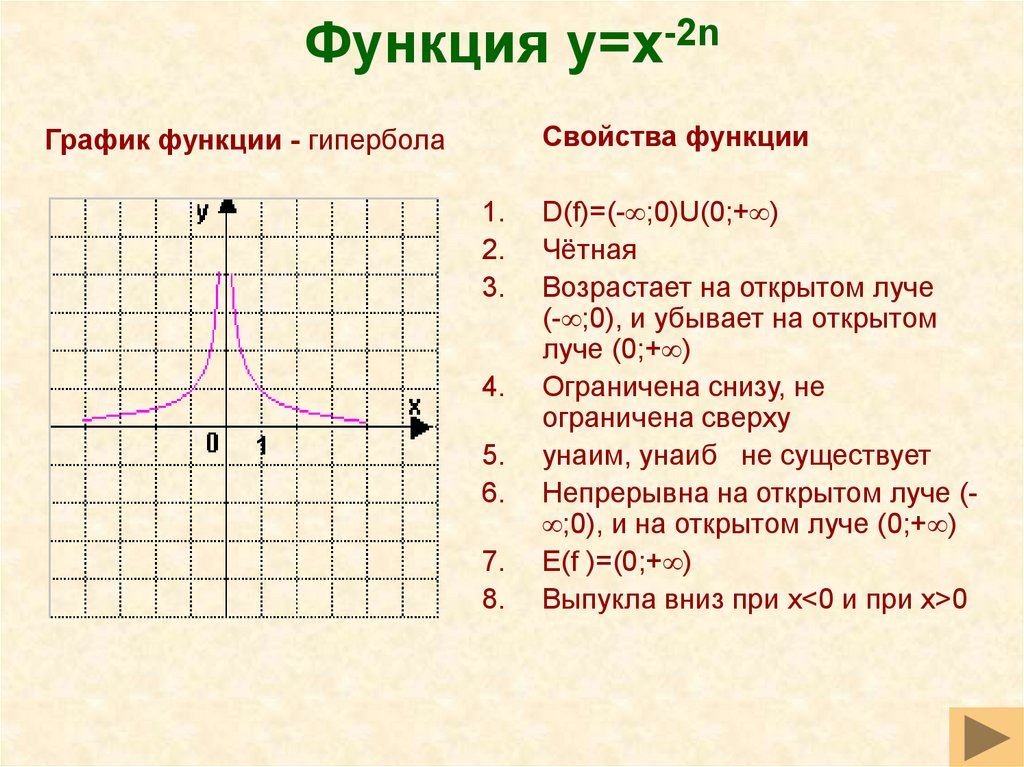
38. Функция y=x-2n
Свойства функцииГрафик функции - гипербола
1.
2.
3.
4.
1
5.
6.
7.
8.
D(f)=(- ;0)U(0;+ )
Чётная
Возрастает на открытом луче
(- ;0), и убывает на открытом
луче (0;+ )
Ограничена снизу, не
ограничена сверху
yнаим, yнаиб не существует
Непрерывна на открытом луче ( ;0), и на открытом луче (0;+ )
E(f )=(0;+ )
Выпукла вниз при x<0 и при x>0
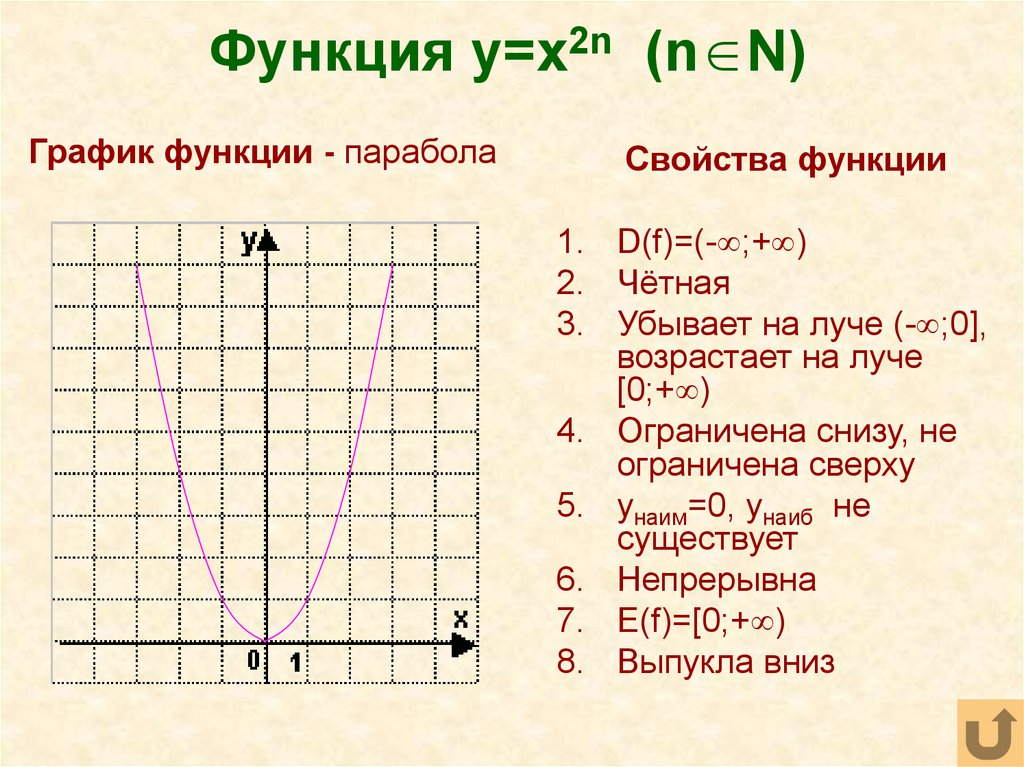
39. Функция y=x2n (n N)
График функции - параболаСвойства функции
1. D(f)=(- ;+ )
2. Чётная
3. Убывает на луче (- ;0],
возрастает на луче
[0;+ )
4. Ограничена снизу, не
ограничена сверху
5. yнаим=0, yнаиб не
существует
6. Непрерывна
7. E(f)=[0;+ )
8. Выпукла вниз


















 mathematics
mathematics








