Similar presentations:
Квадратичная функция, её график и свойства
1. КВАДРАТИЧНАЯ ФУНКЦИЯ, ЕЁ ГРАФИК И СВОЙСТВА
Обзорный материал.2. КВАДРАТИЧНАЯ ФУНКЦИЯ y = ax2 +bx +c И ЕЁ ГРАФИК
Квадратичной функциейназывается функция,
которую можно задать
формулой вида у =ax2+bx+c,
где х—независимая
переменная, a, b и cнекоторые числа, причём a≠0.
1.
2.
3.
Чтобы построить график
квадратичной функции
(параболу), нужно:
Найти координаты вершины
параболы и отметить её в
координатной плоскости.
Построить ещё несколько
точек, принадлежащих
параболе.
Соединить отмеченные
точки плавной линией.
3. ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ у = -х2+2х+8
Графиком функцииявляется парабола, ветви
которой направлены
вверх. Найдём координаты
хв и ув вершины этой
параболы:
хв =-b/2a=-(2)/2·(-1)=1;
y = -12+2·1+8=9.
Отметим эту точку (1;9) в
координатной плоскости.
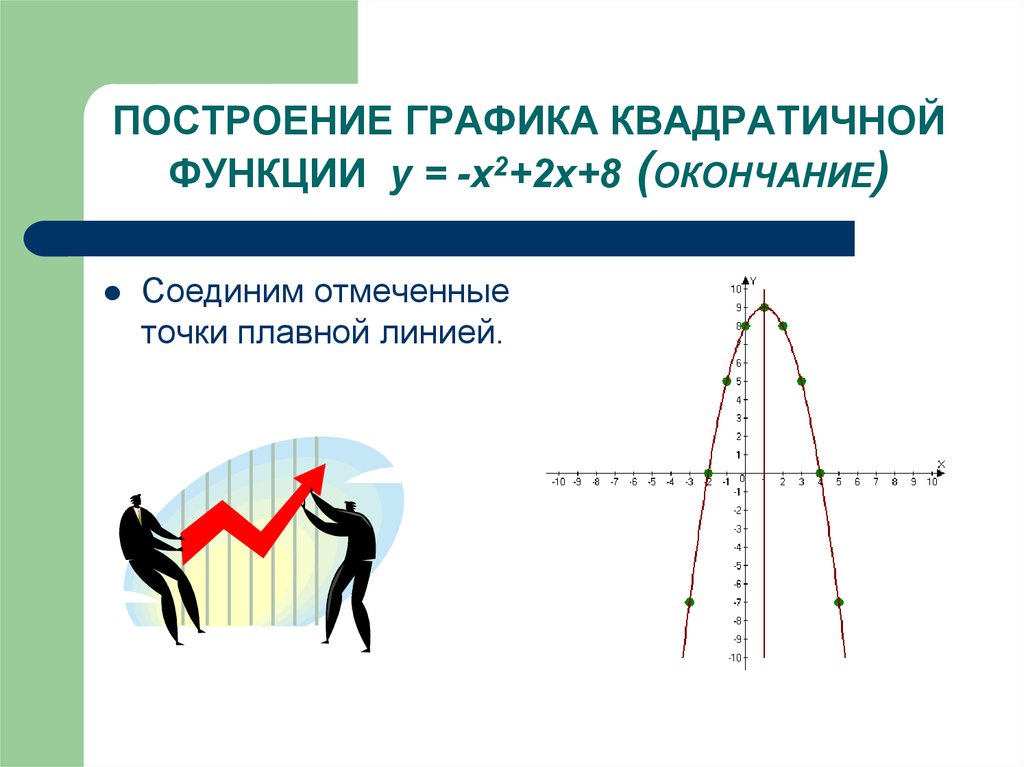
4. ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ у = -х2+2х+8 (продолжение)
Построим ещёнесколько точек,
принадлежащих
параболе:
х -3 -2 -1 0 2 3 4 5
у -7 0 5 8 8 5 0 -7
Прямая х = 1 - ось
симметрии параболы.
5. ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ у = -х2+2х+8 (ОКОНЧАНИЕ)
Соединим отмеченныеточки плавной линией.
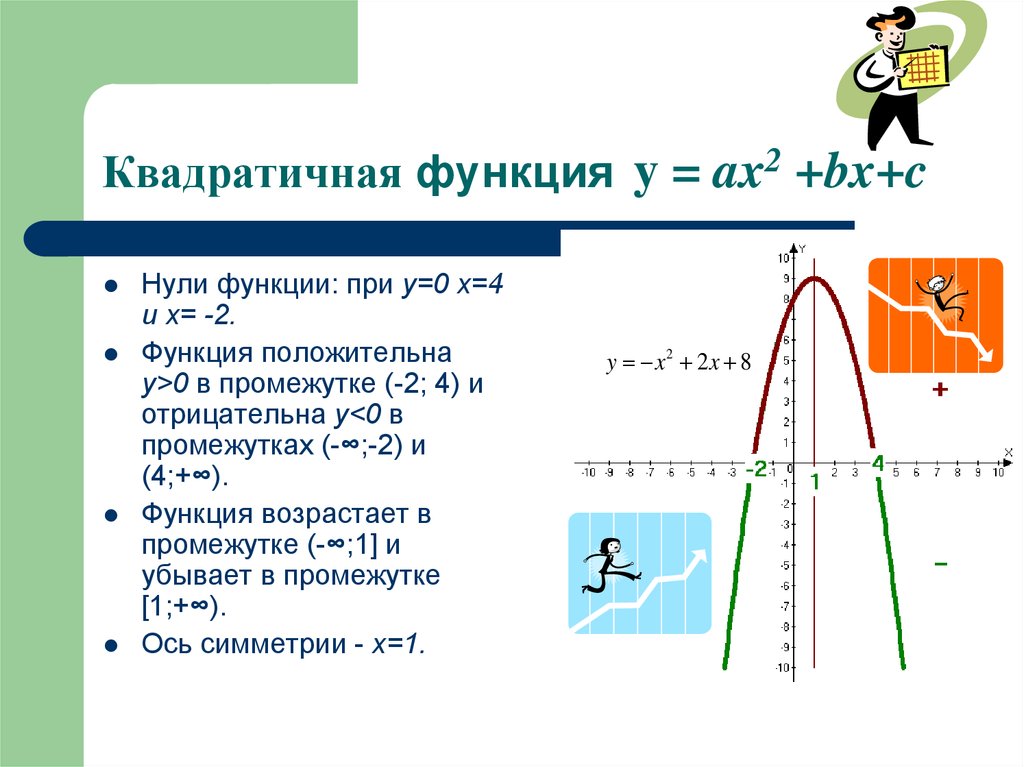
6. Квадратичная функция y = ax2 +bx+c
Нули функции: при у=0 х=4и х= -2.
Функция положительна
у>0 в промежутке (-2; 4) и
отрицательна у<0 в
промежутках (-∞;-2) и
(4;+∞).
Функция возрастает в
промежутке (-∞;1] и
убывает в промежутке
[1;+∞).
Ось симметрии - х=1.
y x2 2 x 8
7. Свойства функции y = ax2 при a>0
Свойства функции y = ax2 при a>0Если х=0, то у=0.
График функции
проходит через
начало координат.
Если х≠0, то у>0.
График функции
расположен в верхней
полуплоскости.
8. Свойства функции y = ax2 при a>0
Свойства функции y = ax2Противоположным
значениям аргумента
(х) соответствуют
равные значения
функции (у). График
функции симметричен
относительно оси у.
при a>0
9. Промежутки убывания и возрастания функции y = ax2
Функция убывает впромежутке (-∞; 0]
(«скатываемся с горки») и
возрастает в промежутке
[0; +∞) («лезем в горку).
Наименьшее значение,
равное нулю, функция
принимает при х=0,
наибольшего значения
функция не имеет.
Областью значений
функции является
промежуток [0;+∞)
10.
1) По графику квадратичной функцииy=f(x), изображённому на
рисунке найдите:
значение у при х=4;
Ответ: при х=4 у=-5;
2) значения х, при которых у=-5;
Ответ: при у=-5 х=0 и 4 ;
3) промежутки возрастания и
убывания функции;
Ответ: функция убывает в интервале
(-∞;2], возрастает-[2; +∞).








 mathematics
mathematics








