Квадратичная функция. Её свойства и график

1. Квадратичная функция. Её свойства и график.

2.

Определение квадратичной
функции
Квадратичной функцией
называется функция , которую можно
задать формулой вида:
y=
2
ax +bx
+c
где: a,b,c –
числа
Х – независимая переменная
а 0

3.

Определить, какие из данных функций
являются квадратичными:
у = 5х2 + 3х
у = х2 – 1
у = 6х3 – 5х2 + 7
у = 6х4 + 5х2 + 7
у = 5х + 2
у= -(х+3)2+2
у = 7х2 + 2х -1
у = х2 – 5х + 6

4.

-
.
Графиком квадратичной функции
у = ах2 + bх + с является парабола,
которая получается из параболы
у = ах2 параллельным переносом.
Вершина параболы - ( х0; уо) ,
b
где : хо = 2a
у0 =
4ac b
4a
2
Осью параболы будет прямая
b
х=2a

5.

Дискриминантом квадратного уравнения
ах2 + bх + с = 0 называется выражение
b2 – 4ac
Его обозначают буквой D, т.е. D= b2 – 4ac.
Возможны три случая:
D 0
D 0
D 0
• если дискриминант больше нуля, то парабола
пересекает ось абсцисс в двух точках,
• если дискриминант равен нулю, то парабола
касается оси абсцисс,
• если дискриминант меньше нуля, то парабола
не пересекает ось абсцисс,

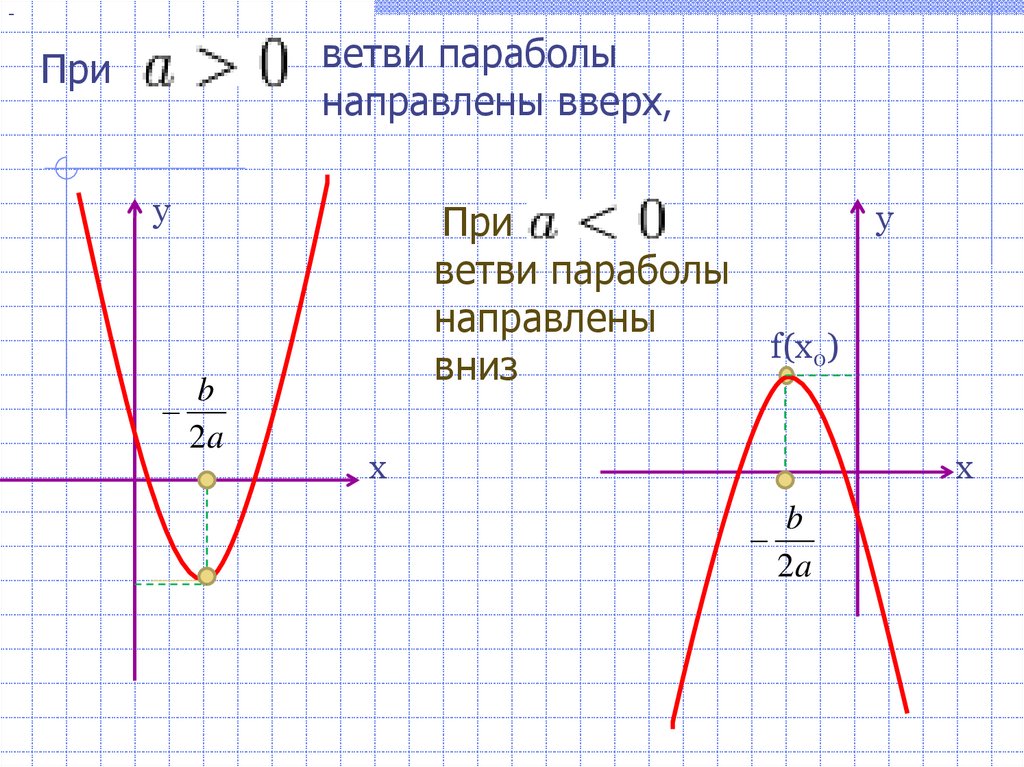
6.

-
ветви параболы
направлены вверх,
При
у
b
2a
При
ветви параболы
направлены
вниз
у
f(x0)
х
х
b
2a

7. Назовите те параболы, ветви которых будут направлены вниз

f(x) = ( х + 2 ) 2 – 3
f(x) = - 3х2 + 1
f(x) = 0,5 х2 – 6х + 5
f(x) = 7х2 + 2х -1
f(x) = - 2 ( х – 3 ) 2 + 4

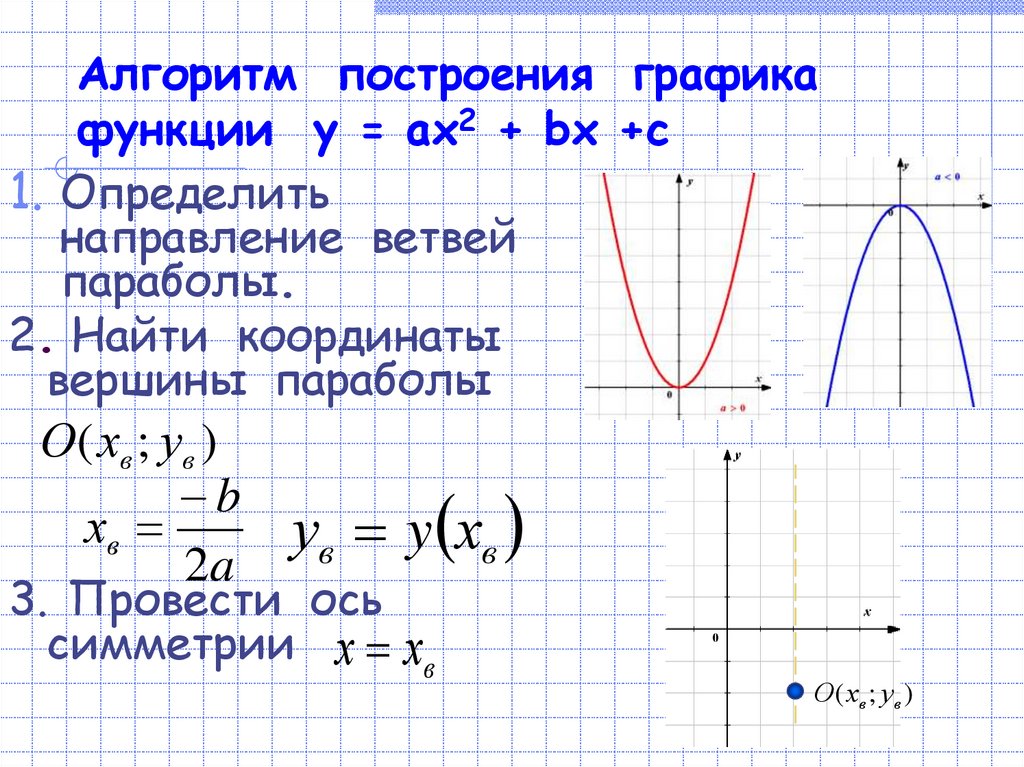
8. Алгоритм построения графика функции у = ах2 + bх +с

1. Определить
направление ветвей
параболы.
2. Найти координаты
вершины параболы
О ( хв ; ув )
b
хв
2a
ув y хв
3. Провести ось
симметрии х хв
О ( хв ; ув )

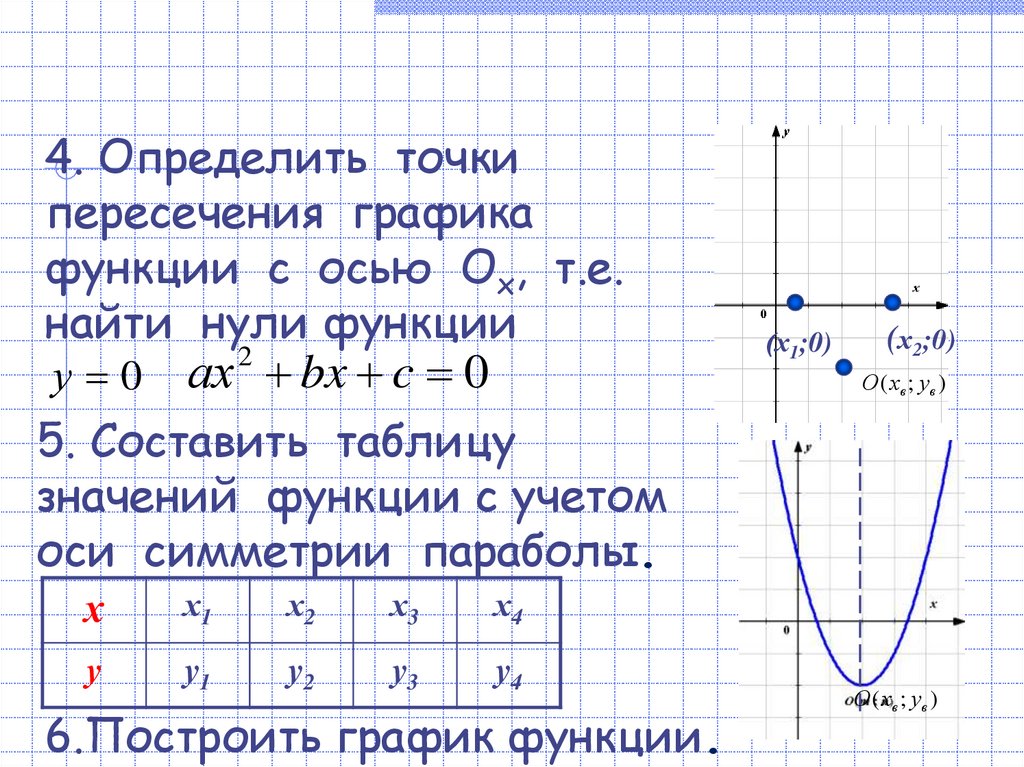
9.

4. Определить точки
пересечения графика
функции с осью Ох, т.е.
найти нули функции
2
у 0 ах bx c 0
(х1;0)
(х2;0)
О ( хв ; ув )
5. Составить таблицу
значений функции с учетом
оси симметрии параболы.
х
х1
х2
х3
х4
у
у1
у2
у3
у4
6.Построить график функции.
О ( хв ; ув )

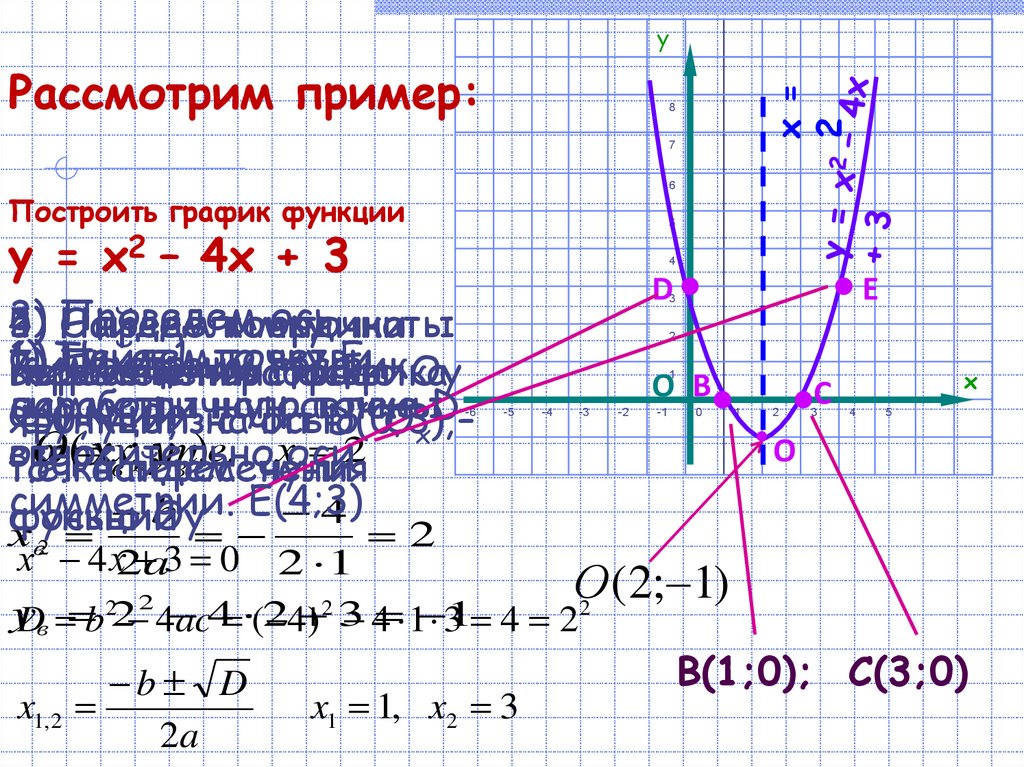
10.

Рассмотрим пример:
х =
2
у
8
7
6
Построить график функции
5
у = х2 – 4х + 3
4
3)
Проведем
ось
2) Найдем
4)
5)
Определим
координаты
точку
точки
1)
6)
Т.к.
Найдем
а=1,параболы
то
точку
Е Оу
симметрии
7)
Построим
график
вершины
пересечения
пересечения
светви
графика
осью
параболы
симметричную
направлены
точке
функции
х=0,
функции
у=3, значит
с осью
D(0;3)
ОхD, –
х;в ,ут
.е. хоси
2
Ох ( хнайдем
вверх.
относительно
впересечения
в)
т.е.
точка
нули
симметрии.
Е(4;3)
b
4
функции
с
осью
Оу
х
2
-6
D
Е
3
2
1
О В
-5
-4
-3
-2
-1
0
1
2
С
3
х
4
5
О
хв2 4 х2 a3 0 2 1
О
(
2
;
1
)
2
уDв b22 4
ac4 (2
4
)2 3
4 1 31 4 22
x1, 2
b D
2a
x1 1, x2 3
В(1;0); С(3;0)

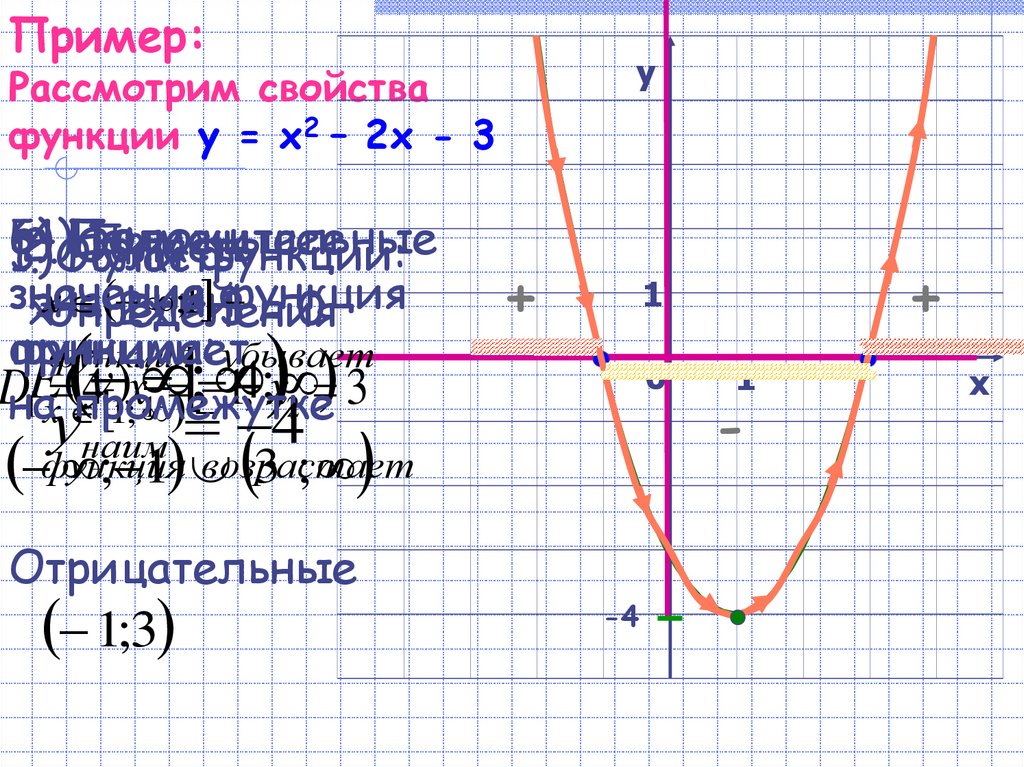
11. Пример: Рассмотрим свойства функции у = х2 – 2х - 3

Пример:
у
Рассмотрим свойства
функции у = х2 – 2х - 3
6)
5)
4)Область
Положительные
Наименьшее
При функции:
Область
3)
Нули
1.2.
значения
значение
функция
2 –
хопределения
;1- 3
=0
хзначений
2х
принимает
функции:
функция убывает
Е
(
у
)
4
;
;
Dна
4
x
1
,
x
3
1х
1
2
промежутке
у 1; 4
+
0
возрастает
функция
3 ;
; 1
наим
Отрицательные
1;3
+
1
-4
1
-
х

12.

Решив квадратное
уравнение х 2 - 6 х + 8 =0
определяем нули функции
Х=2 иХ=4
а > 0 (Ветви параболы
направлены вверх)
Точка пересечения с осью
ординат (0 ; 8)
Ось симметрии
Построим график
у =х2-6х +8
х = -(b/ 2a)
y=9-18+8=-1
( 3; -1)- вершина параболы

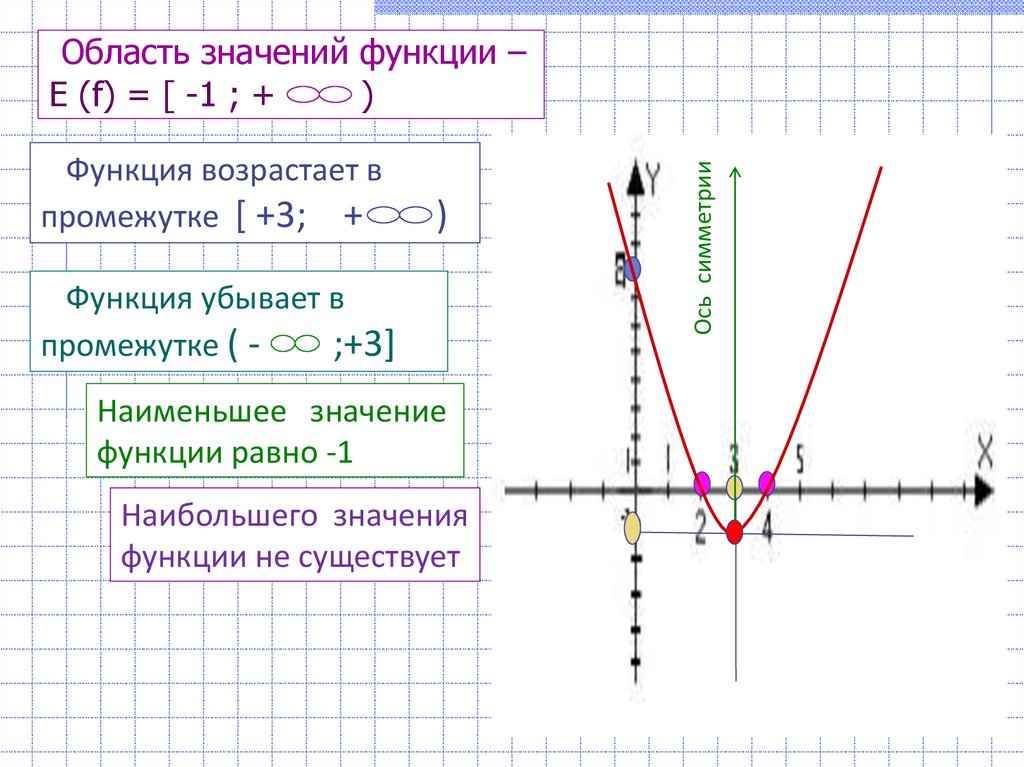
13. Область значений функции – Е (f) = [ -1 ; + )

Функция возрастает в
промежутке [ +3; +
)
Функция убывает в
промежутке ( ;+3]
Наименьшее значение
функции равно -1
Наибольшего значения
функции не существует
Ось симметрии
Область значений функции –
Е (f) = [ -1 ; +
)

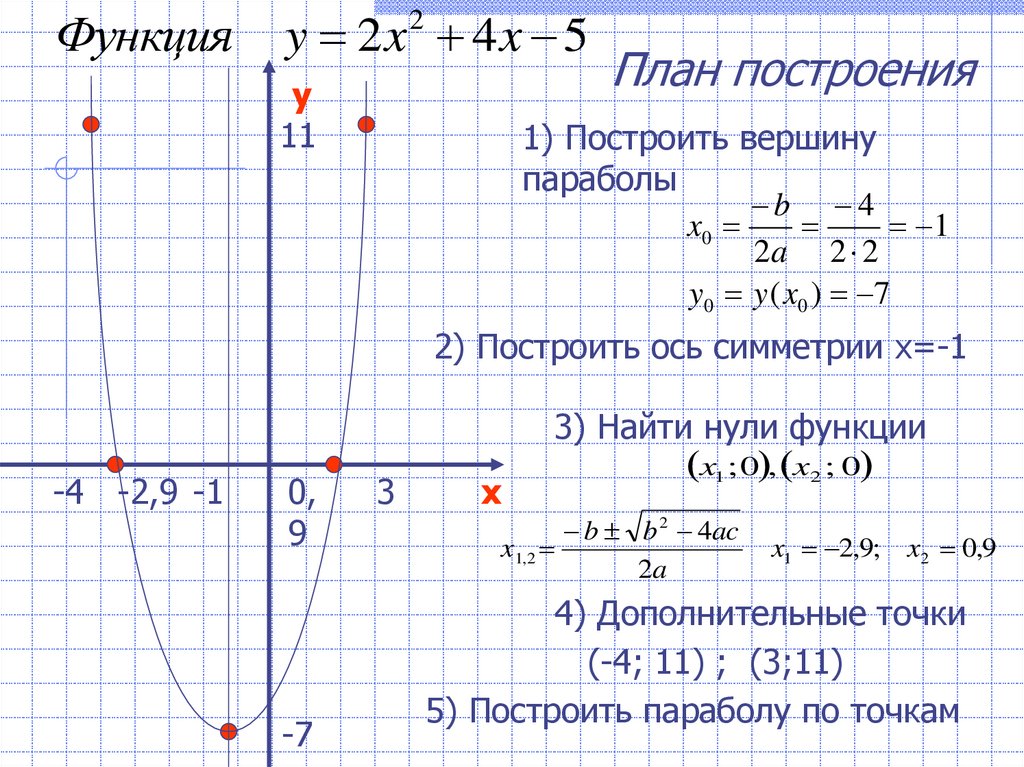
14.

Функция
y 2x 4x 5
2
y
11
План построения
1) Построить вершину
параболы
b 4
x0
1
2a 2 2
y 0 y ( x0 ) 7
2) Построить ось симметрии x=-1
-4 -2,9 -1
0,
9
-7
3
x
3) Найти нули функции
x1 ; 0 , x2 ; 0
b b 2 4ac
x1, 2
2a
x1 2,9; x2 0,9
4) Дополнительные точки
(-4; 11) ; (3;11)
5) Построить параболу по точкам

15.

Спасибо
за
внимание!