Similar presentations:
Квадратичная функция, ее график и свойства
1. Квадратичная функция. Её свойства и график.
2.
Определение квадратичнойфункции
Квадратичной функцией называется
функция , которую можно задать формулой
вида:
y=
2
ax +bx
+c
где: a, b, c –
числа
Х – независимая переменная
а 0
График квадратичной функции – парабола.
3. Алгоритм построения параболы у = ах2 + bх + с :
1. Найти координаты вершины параболы, построитьна координатной плоскости соответствующую точку,
провести ось симметрии.
2.
Определить направление ветвей параболы.
3. Найти координаты еще нескольких точек,
принадлежащих искомому графику ( в частности,
координаты точки пересечения параболы с осью у и
нули функции, если они существуют).
4. Отметить на координатной плоскости
найденные точки и соединить их плавной линией.
4.
-.
Графиком квадратичной функции
у = ах2 + bх + с является парабола, которая получается из
параболы
у = ах2 параллельным переносом.
Вершина параболы - ( х0; уо) ,
b
где : хо = 2a
у0 =
4ac b 2
4a
Осью параболы будет прямая
b
х=2a
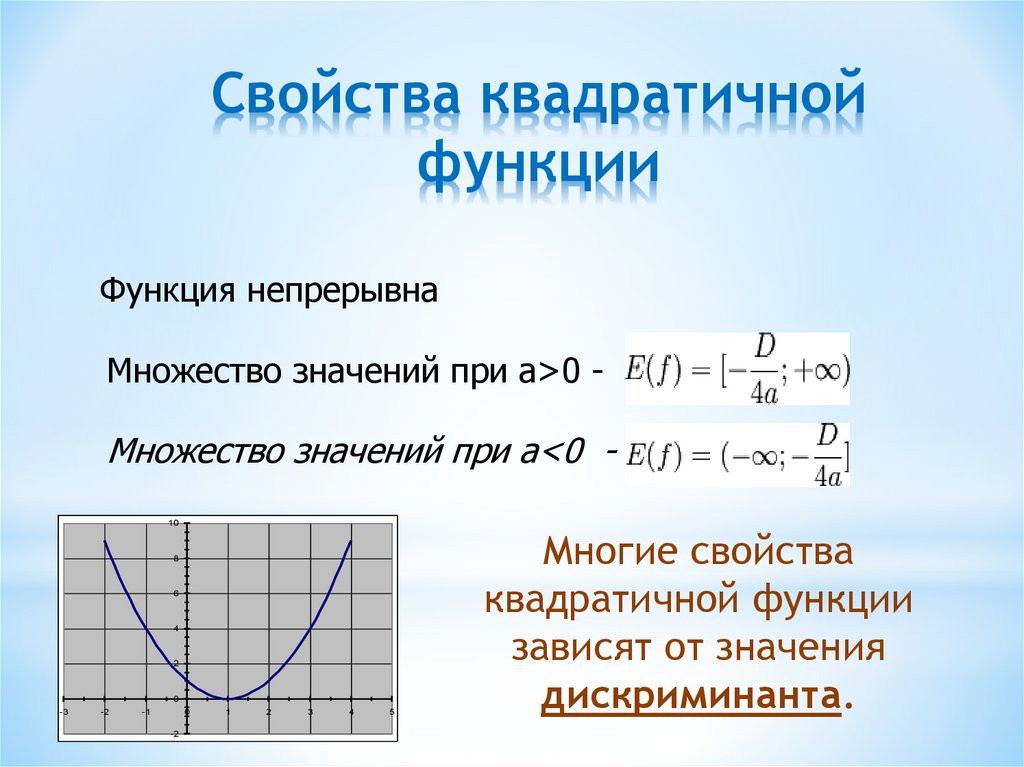
5. Свойства квадратичной функции
Функция непрерывнаМножество значений при a>0 -
Множество значений при a<0 10
8
6
4
2
0
-3
-2
-1
0
-2
1
2
3
4
5
Многие свойства
квадратичной функции
зависят от значения
дискриминанта.
6.
Дискриминантом квадратного уравненияах2 + bх + с = 0 называется выражение
D =b2 – 4ac
Возможны три случая:
D 0
D 0
D 0
7.
если дискриминант больше нуля, то параболапересекает ось абсцисс в двух точках,
если дискриминант равен нулю, то парабола
касается оси абсцисс,
если дискриминант меньше нуля, то парабола не
пересекает ось абсцисс,
абсцисса вершины параболы равна
8.
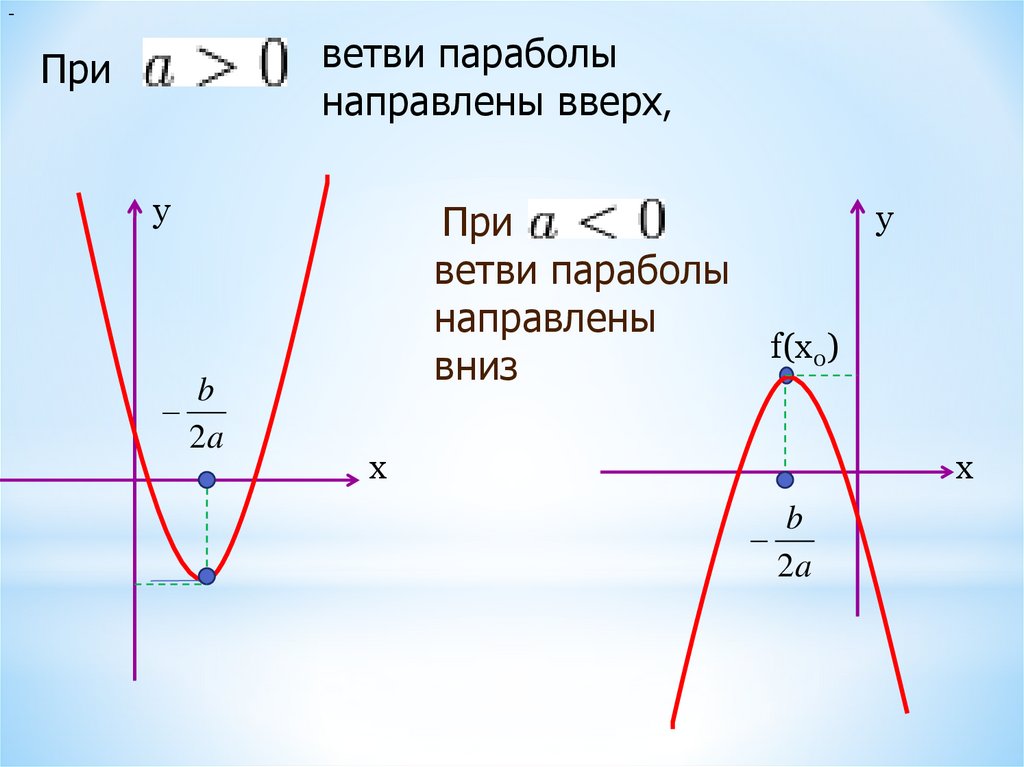
-ветви параболы
направлены вверх,
При
у
b
2a
При
ветви параболы
направлены
вниз
у
f(x0)
х
х
b
2a
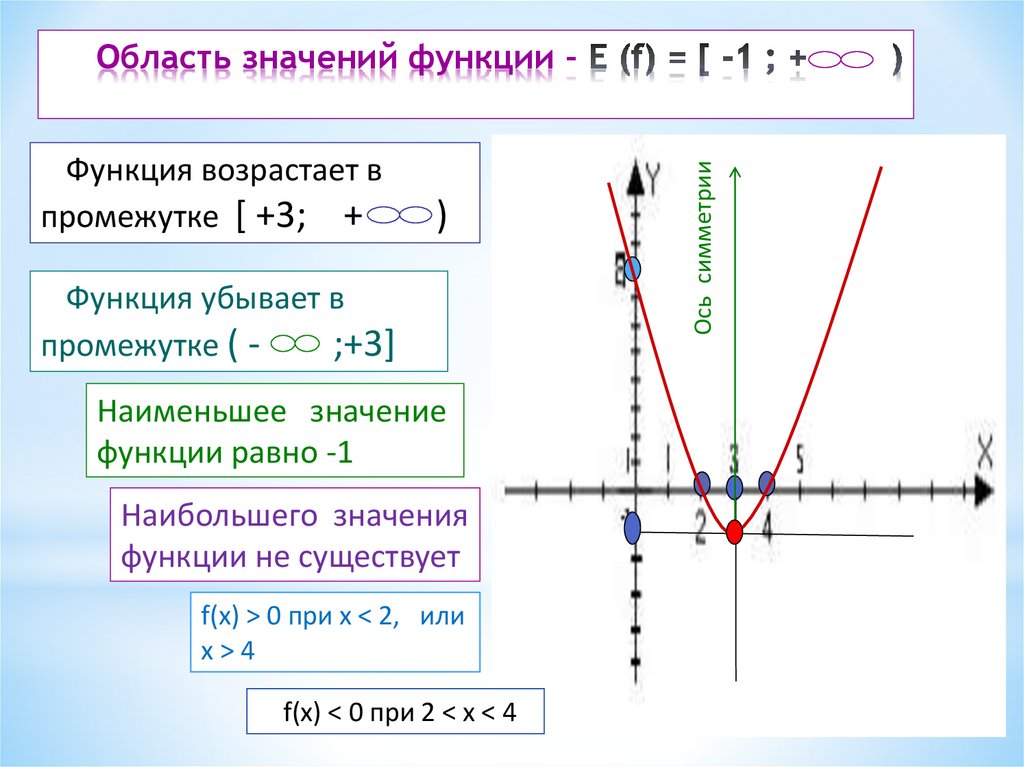
9. Область значений функции – Е (f) = [ -1 ; + )
Функция возрастает впромежутке [ +3; +
)
Функция убывает в
промежутке ( ;+3]
Наименьшее значение
функции равно -1
Наибольшего значения
функции не существует
f(x) > 0 при х < 2, или
х>4
f(x) < 0 при 2 < х < 4
Ось симметрии
Область значений функции –
10. Постройте график функции у=2х²+4х-6, опишите его свойства
11.
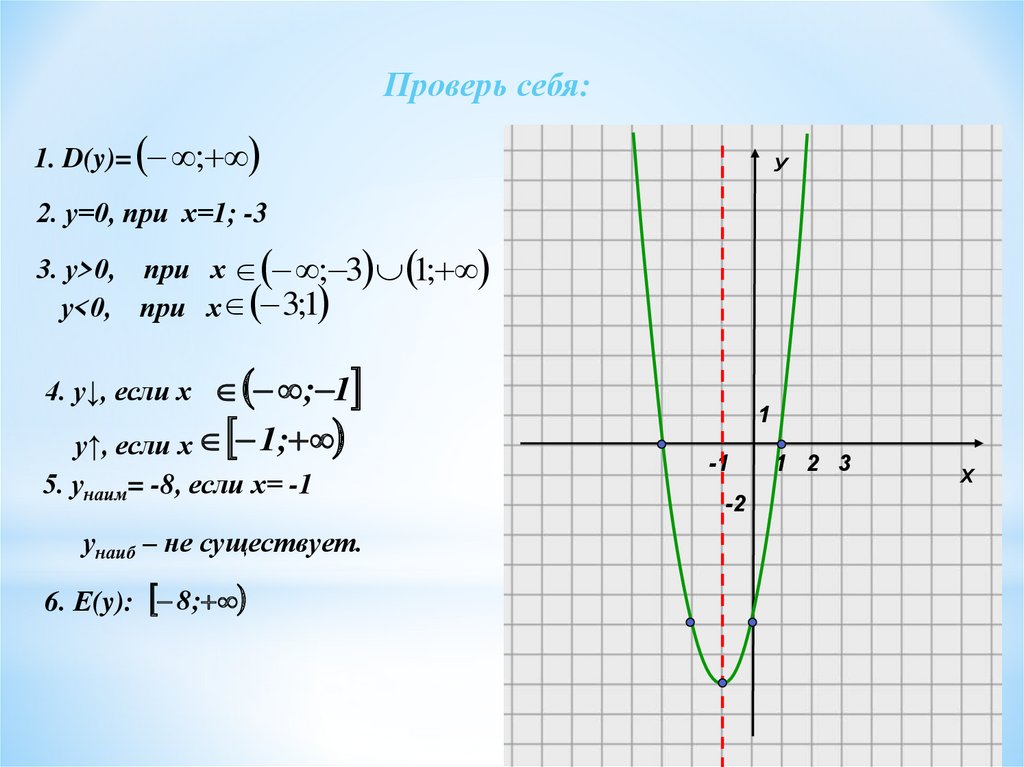
Проверь себя:1. D(y)=
;
У
2. у=0, при х=1; -3
3. у>0, при х ; 3 1;
у<0, при х 3;1
4. у↓, если х ; 1
у↑, если х 1;
5. унаим= -8, если х= -1
унаиб – не существует.
6. Е(y): 8 ;
1
-1
-2
1 2 3
Х
12.
Задание1. Построить график функции и
описать ее свойства у=2х²+4х-1
2. Построить график функции и
описать ее свойства у= -7х²-х+3








 mathematics
mathematics







