Similar presentations:
Квадратичная функция, ее график и свойства
1. Квадратичная функция, ее график и свойства
КВАДРАТИЧНАЯ ФУНКЦИЯ, ЕЕ ГРАФИКИ СВОЙСТВА
2.
00
3.
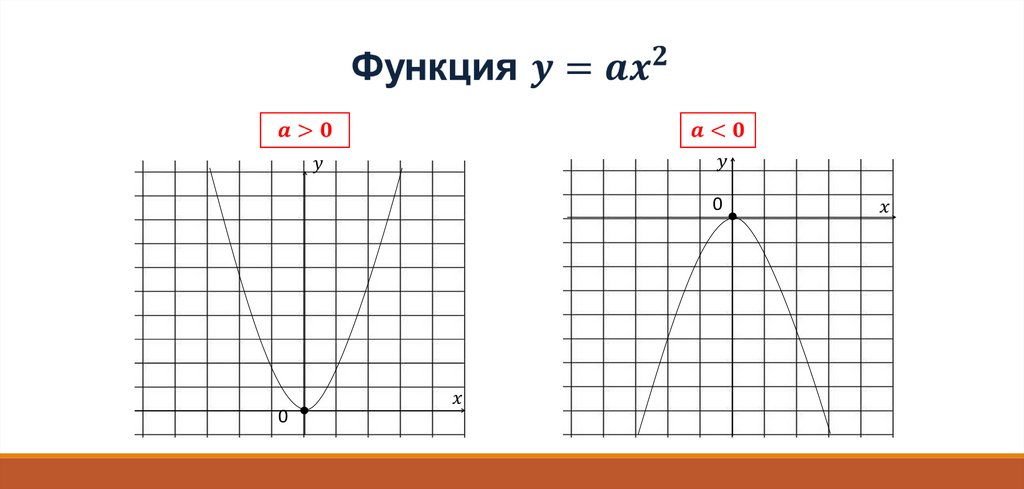
Графиком функциипри любом а = 0 является парабола с
вершиной в начале координат
Ось симметрии – Ось ординат
При а > 0 ветви параболы направлены вверх
При а < 0 ветви параболы направлены вниз
4.
Определение.2
ах +bх+с,
Функция вида у =
где а, b, c – заданные числа,
а ≠ 0, х – действительная переменная,
называется квадратичной функцией.
5.
Графиком функцииу=
2
ах +bх+с
при любом а = 0 является парабола
При а > 0 ветви параболы направлены вверх
При а < 0 ветви параболы направлены вниз
6.
1.Коэффициент а влияет на направление
ветвей параболы:
при а > 0 – ветви направлены вверх,
при а < 0 – вниз.
2. Коэффициент b влияет на расположение
вершины параболы:
при b = 0 вершина лежит на оси ОУ.
3.
Коэффициент
с
показывает
точку
пересечения параболы с осью ОУ.
7.
Найти координаты вершины параболы:У =2(х-4)² +5
(4;5)
У =-6(х-1)²
(1;0)
У = -х²+12
(0;12)
У = х²+4
(0;4)
У = (х+7)² - 9
(-7;-9)
У = 6 х²
(0;0)
8.
Найти координаты вершины параболы:У =2(х-4)² +5
(4;5)
У = -х²+12
(0;12)
У = (х+7)² - 9
(-7;-9)
У =-6(х-1)²
(1;0)
У = х²+4
(0;4)
У = 6 х²
(0;0)
9.
Алгоритм построения графика функции10.
Алгоритм исследования графика функции1. найти Область определения функции
2. найти Область значения функции
3. Определить промежутки, в которых функция возрастает/убывает
4. Определить промежутки, в которых функция принимает
положительные/отрицательные значения
5. Определить наибольшее (наименьшее) значение параболы
11.
Построить график функцииy=
2
х
+ 2х - 8
12.
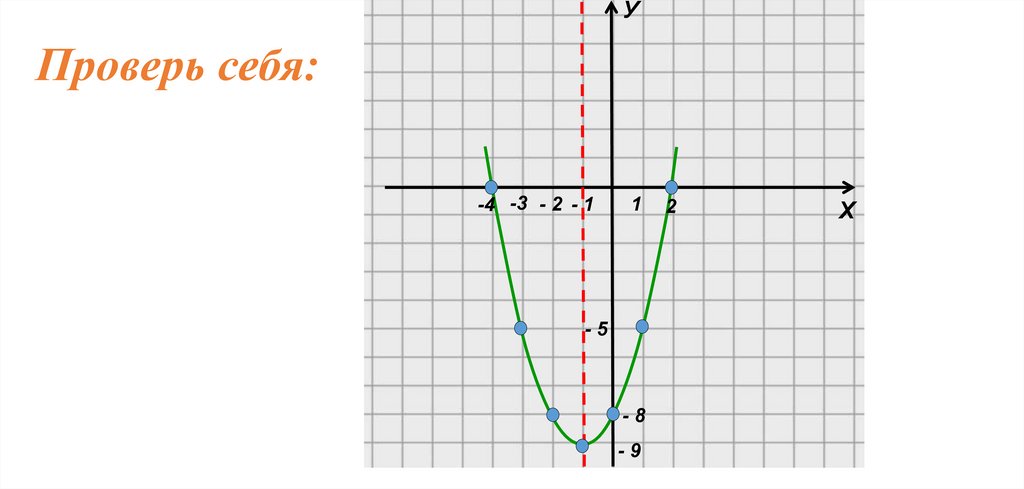
Проверь себя:y=
2
х
+ 2х - 8
1. Ветви параболы направлены вверх, т. к. а = 1 (1>0)
2. Вершина параболы: т. А (-1; - 9)
3. Ось симметрии: х0 = - 1
4. Нули функции:
Точки пересечения с ОХ : (- 4; 0); (2; 0)
Точки пересечения с ОУ : (0; - 8)
5.
х - 3 - 2 -1 0 1
у -5 -8 -9 -8 -5
13.
УПроверь себя:
-4 -3 - 2 - 1
1
-5
-8
-9
2
Х
14.
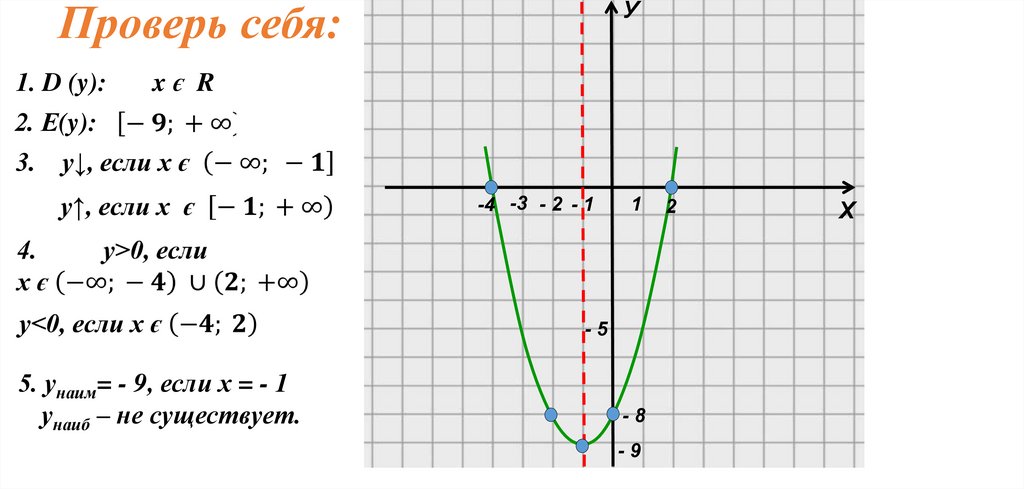
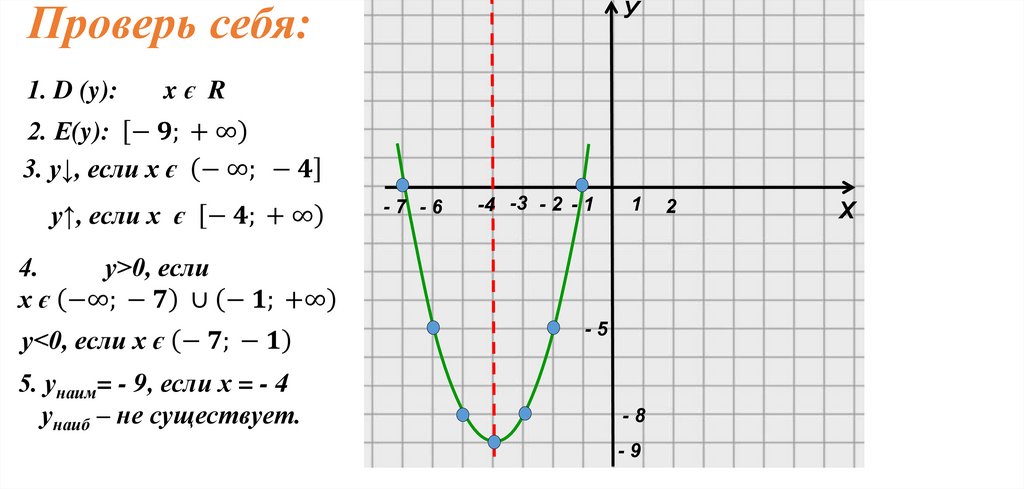
Проверь себя:1. D (y):
У
xє R
2. Е(y):
-4 -3 - 2 - 1
1
-5
5. унаим= - 9, если х = - 1
унаиб – не существует.
-8
-9
2
Х
15.
Построить график функцииy=
2
х
+ 8х + 7
16.
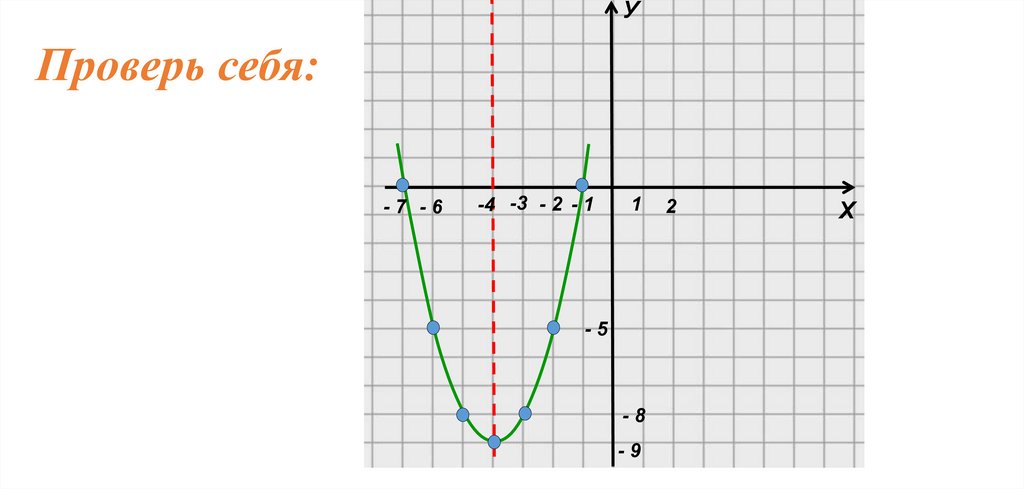
Проверь себя:y=
2
х
+ 8х + 7
1. Ветви параболы направлены вверх, т. к. а = 1 (1>0)
2. Вершина параболы: т. А (-4; - 9)
3. Ось симметрии: х0 = - 4
4. Нули функции:
Точки пересечения с ОХ : (- 7; 0); (- 1; 0)
Точки пересечения с ОУ : (0; 7)
х
7
6
5
4
5.
у
0
-5
-8
-9
-3
-2
-1
-8
-5
0
17.
УПроверь себя:
-7 -6
-4 -3 - 2 - 1
1
-5
-8
-9
2
Х
18.
Проверь себя:1. D (y):
У
xє R
2. Е(y):
-7 -6
-4 -3 - 2 - 1
1
-5
5. унаим= - 9, если х = - 4
унаиб – не существует.
-8
-9
2
Х
19.
20.
Резервное задание:Не выполняя построения графика функции у = определите направление её ветвей.
2
4х
+ 4х + 3, ,
Не выполняя построения графика функции, найдите значение
х, при котором функция у = - 4х2 + 4х + 3 принимает
наибольшее значение, и найдите это значение
2
4х
Не выполняя построения графика функции у = + 4х + 3, ,
определите промежутки возрастания (убывания) функции
21.
Итоги урокаСформулируйте алгоритм построения квадратичной
функции
Если а > 0 то, какое значение имеет функция?
Если а < 0 то, какое значение имеет функция?
В какой точке функция у = ах2 + bх + с принимает
наибольшее или наименьшее значение?













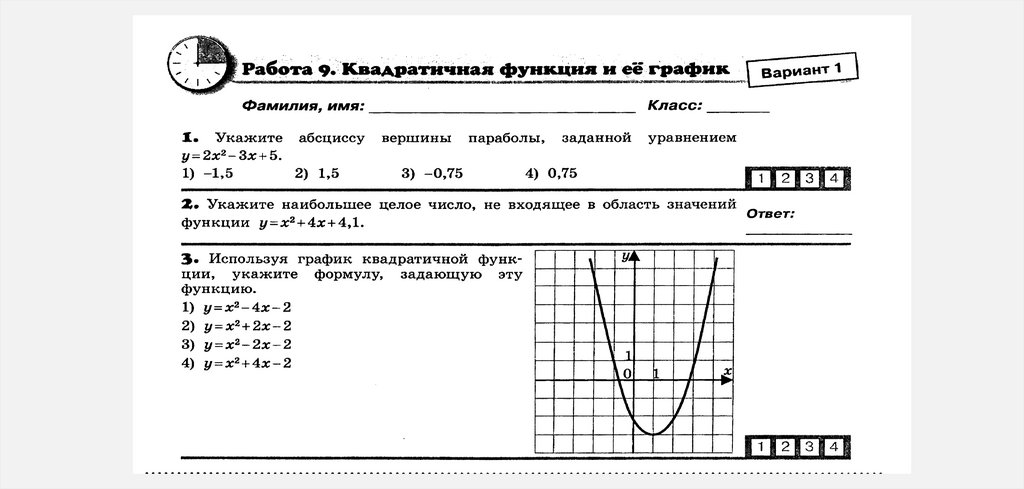


 mathematics
mathematics







