Квадратичная функция. Ее свойства и график

1. Падение баскетбольного мяча

2. Параболический фонтан

3. Библиотека с крышей в форме параболы в норвегии

4. Лучи прожектора

5. Параболическая солнечная электростанция в калифорнии, США

6. Вращающийся сосуд с жидкостью

7.

8.

9.

Квадратичная
функция

10.

Определение:
Квадратичной функцией
называется функция, которую
можно записать формулой вида
y = ax2 + bx + c, где x – независимая
переменная, a, b и c – некоторые
числа, причем a≠0.

11.

Из предложенных функций
выберите квадратичную функцию
4
1
) у
х
2
2
) у 6 х
х
3
) у 2
х 8
4
) у 5 6х
5
) у (х 7
) 1
2
6
) у 6х

12.

Алгоритм построения графика
функции у = ах2 + bх +с
1. Определить
направление ветвей
параболы.
2. Найти координаты
вершины параболы
О(хв ; ув )
b
хв
2a
ув y хв
О(хв ; ув )

13.

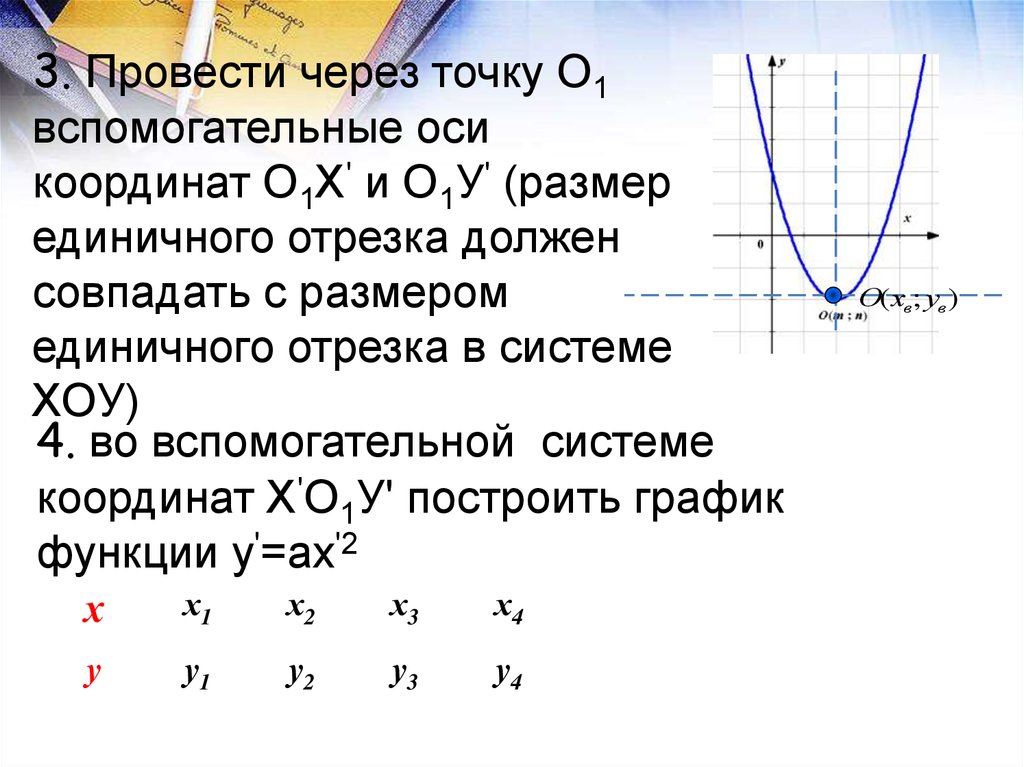
3. Провести через точку О1
вспомогательные оси
координат О1Х' и О1У' (размер
единичного отрезка должен
совпадать с размером
единичного отрезка в системе
ХОУ)
4. во вспомогательной системе
координат Х'О1У' построить график
функции у'=ах'2
х
х1
х2
х3
х4
у
у1
у2
у3
у4
О(хв ; ув )

14.

у
х = 2
Рассмотрим пример:
8
7
6
Построить график функции
5
у = х2 – 4х + 3
4
4)
во вспомогательной
системе
3)
Проведем
2)
Найдем
координаты
1) Т.к. а=1, то' ветви
координат
Х
О
У'
постройте
дополнительные
оси
1
вершины
параболы
параболы направлены
график функции у'=ах'2
х
.е
. х
2
О
(
хвх
;в,
ут
вверх.
в)
-6
-5
b
4
х
2
в
2
a
2
1
2
у
2
4
2
3
1
в
-4
-3
D3
Е
2
О1
-2
-1
х
С
0
1
2
О
3
4
5
О(2; 1)
В(1;0); С(3;0)

15.

Свойства квадратичной функции
у = ах2 + bх +с, при а>0
D>0
D=0
D<0
1. Область
определения
2. Область
значений
3. Нули функции
4.Возрастание
убывание
функции
5.Положительны
е отрицательные
значения функции
6.Наибольшее
или наименьшее
значение функции
Для у=ах2+bх+с, при а<0, заполните таблицу самостоятельно

16.

Пример:
у
Рассмотрим свойства
функции у = х2 – 2х - 3
6)
5)
4)Область
Положительные
Наименьшее
При функции:
Область
3)
Нули
1.2.
значения
значение
функция
2
х
;1
= 0
хзначений
–
2х
- 3
определения
принимает
функции:
функция
убывает
Е
(у
)
4
;
;
D
4
x
1
,
x
3
1
1
2
на
промежутке
х 1;
у
4
+
0
функция
возрастает
3;
;
1
наим
Отрицательные
1;3
+
1
-4
1
-
х

17.

Ответьте на
вопросы:
1. Назовите координаты
вершины параболы;
2. Назовите ось
симметрии параболы;
3. Назовите нули
функции;
4. Назовите промежутки
возрастания и убывания
функции;
5. При каких значениях х,
значения функции
положительны, а при
каких отрицательны;
6. Назовите наибольшее
или наименьшее
значение функции.
у
1
0
1
х

18.

Спасибо за урок.