Similar presentations:
Квадратичная функция. Её свойства и график
1. Квадратичная функция. Её свойства и график.
2.
Определение.Функция вида у = ах2+bх+с,
где а, b, c – заданные числа,
а ≠ 0, х – действительная
переменная,
называется
квадратичной функцией.
3.
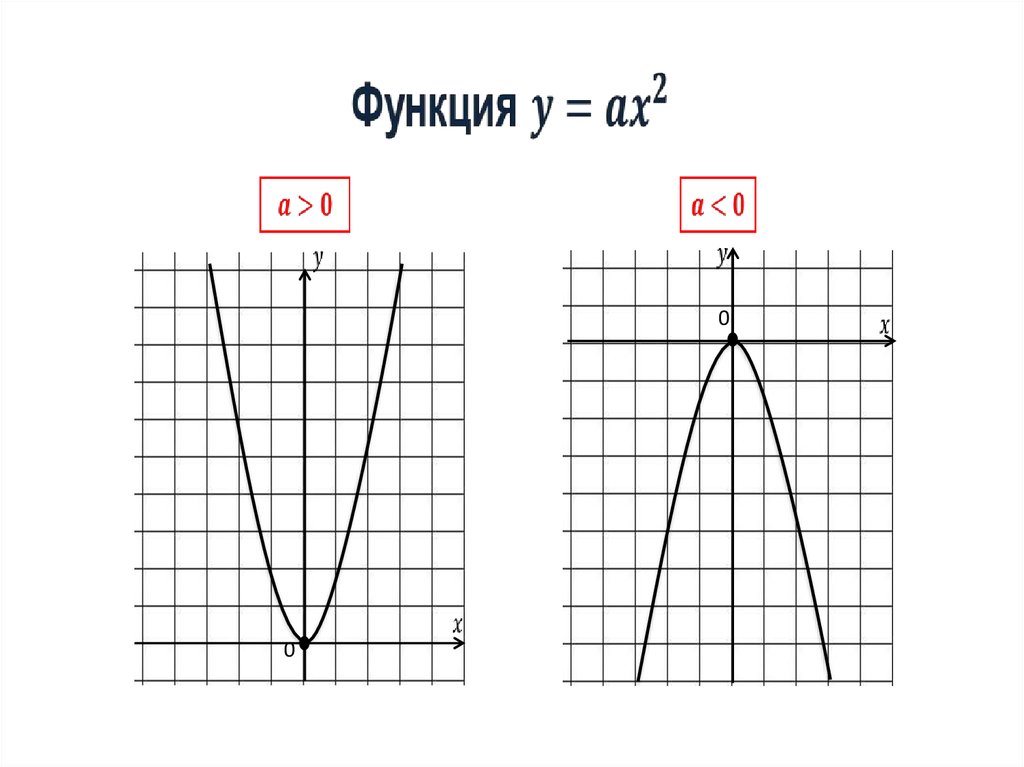
Коэффициент а влияет на направлениеветвей параболы:
при а > 0 – ветви направлены вверх,
при а < 0 – вниз.
2. Коэффициент b влияет на расположение
вершины параболы:
при b = 0 вершина лежит на оси ОУ.
3.
Коэффициент
с
показывает
точку
пересечения параболы с осью ОУ.
1.
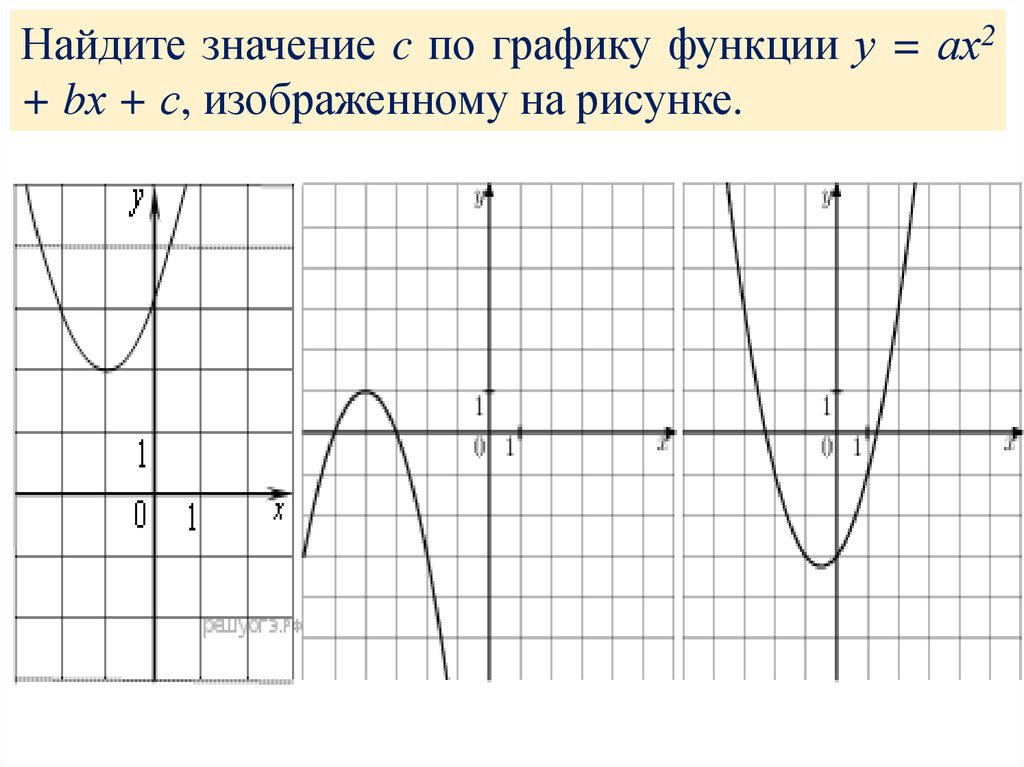
4.
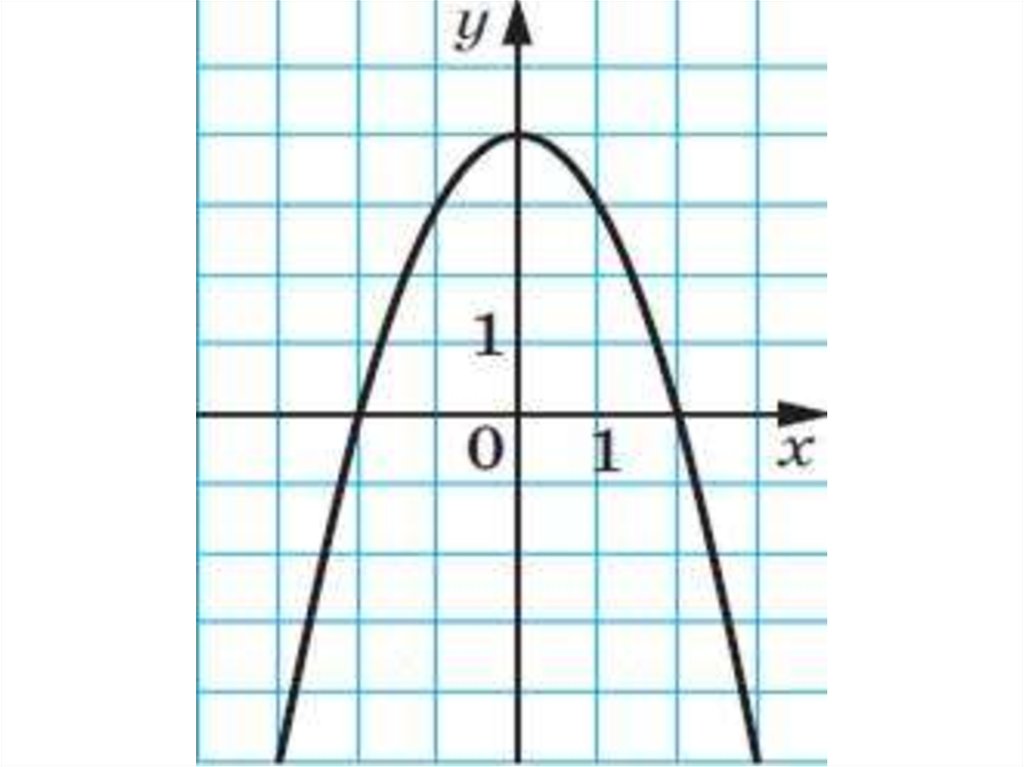
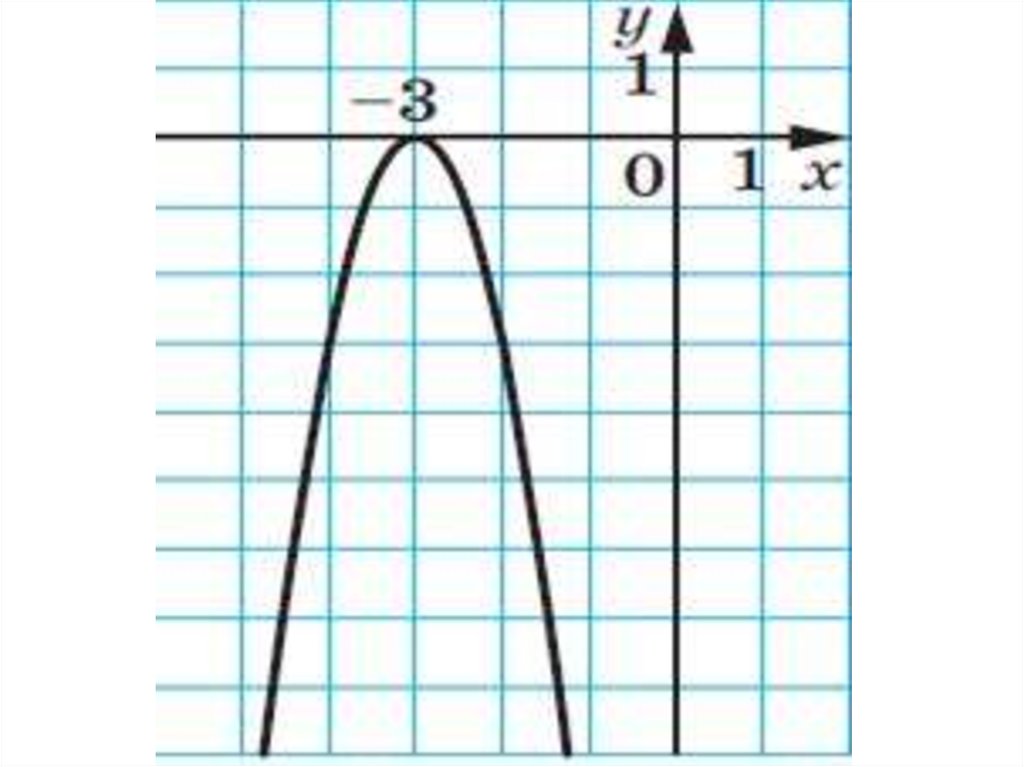
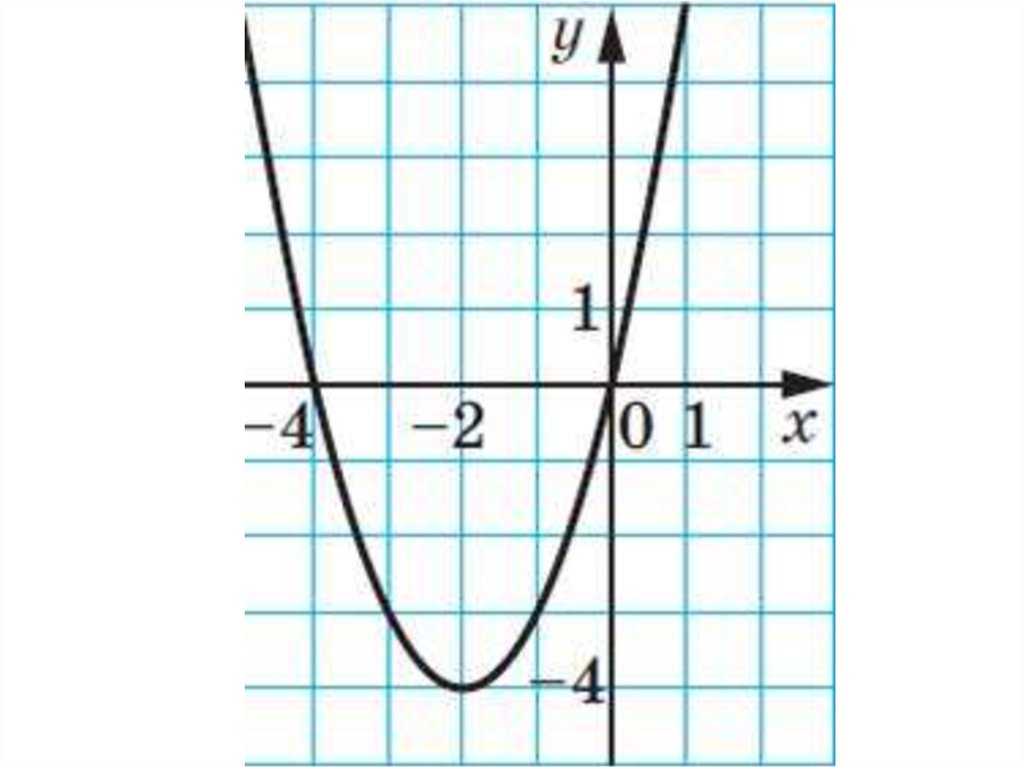
Найдите значение c по графику функции у = ах2+ bх + с, изображенному на рисунке.
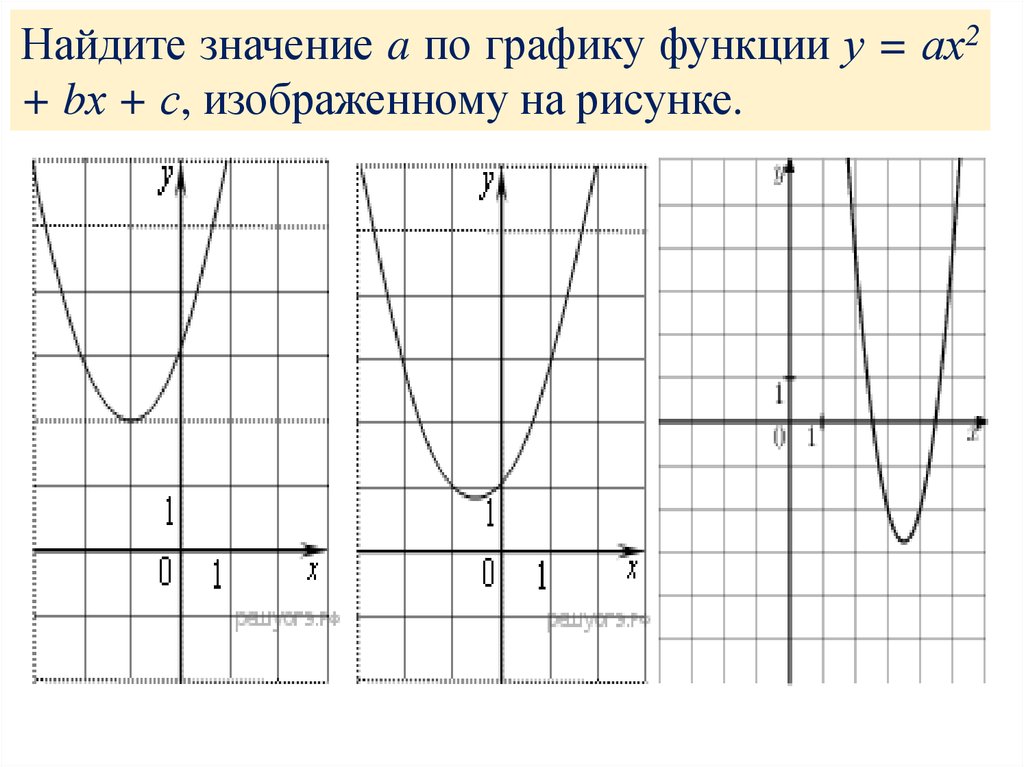
5.
Найдите значение a по графику функции у = ах2+ bх + с, изображенному на рисунке.
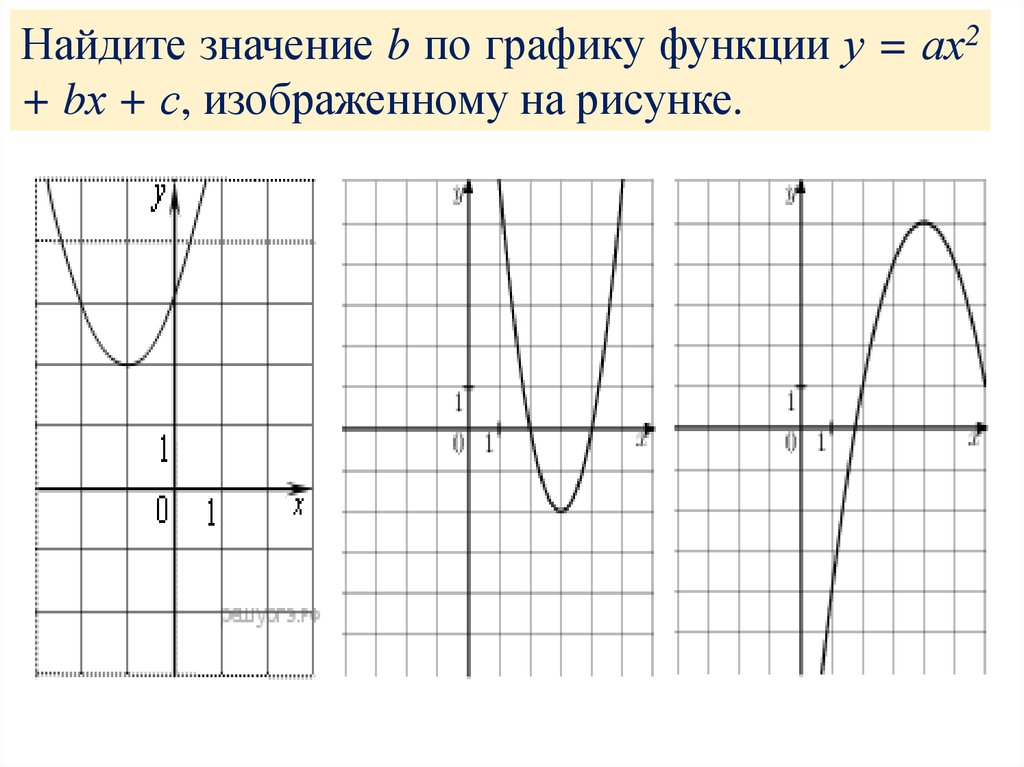
6.
Найдите значение b по графику функции у = ах2+ bх + с, изображенному на рисунке.
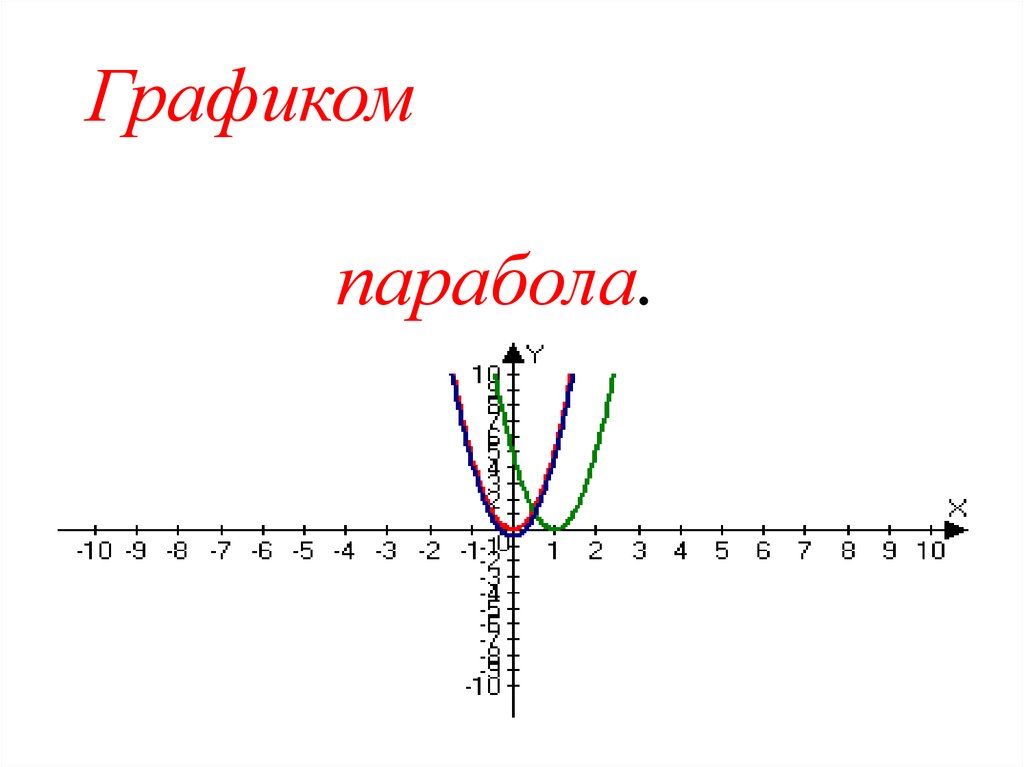
7. Графиком квадратичной функции является парабола.
8.
00
9.
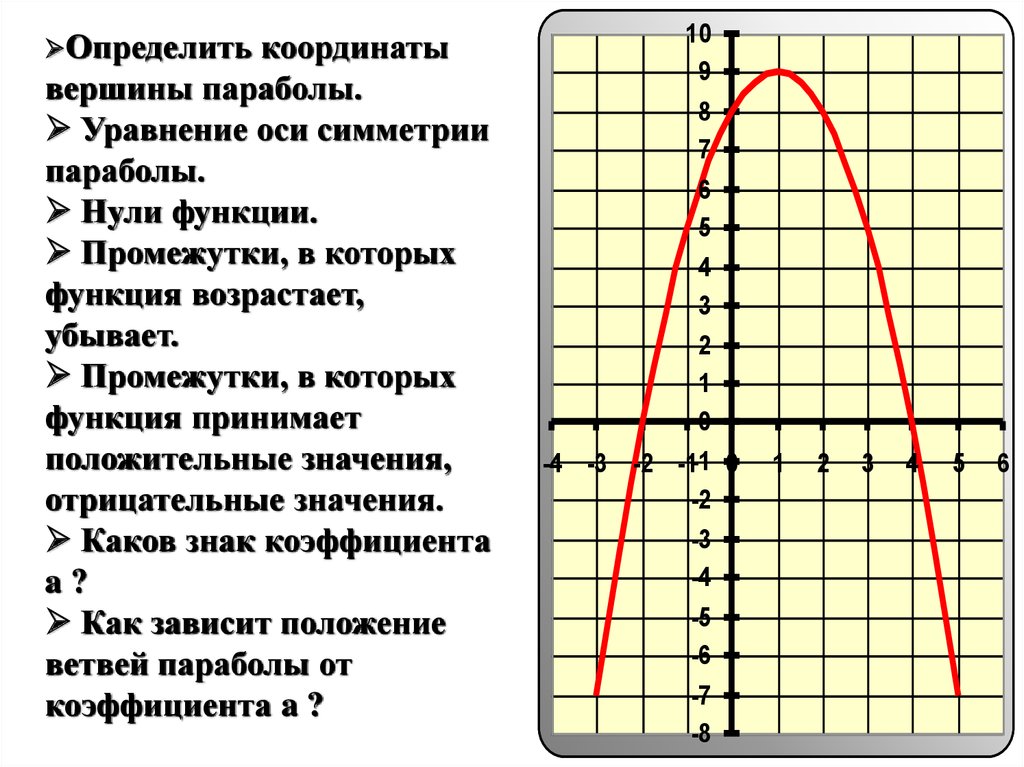
Определитькоординаты
вершины параболы.
Уравнение оси симметрии
параболы.
Нули функции.
Промежутки, в которых
функция возрастает,
убывает.
Промежутки, в которых
функция принимает
положительные значения,
отрицательные значения.
Каков знак коэффициента
a?
Как зависит положение
ветвей параболы от
коэффициента a ?
10
9
8
7
6
5
4
3
2
1
0
-4 -3 -2 -1-1 0
-2
-3
-4
-5
-6
-7
-8
1
2
3
4
5
6
10.
Заполни пропуски …1).Функция у = aх2 + bx + c, где а, b, c – заданные действительные
числа, а 0, х – действительная переменная, называется … функцией.
квадратичной
2).График функции у = ах2 при любом а 0 называют
параболой
….
3).Функция у = х2 является … (возрастающей, убывающей) на
промежутке х 0.
убывающей
4).Значения х, при которых квадратичная функция равна нулю, называют
функции.
нулями функции
5).Точку пересечения параболы с осью симметрии называют …
параболы.
вершиной параболы
6).При а >0 ветви параболы у = ах2 направлены … .
вверх
7).Если а< о и х 0, то функция у = ах2 принимает
… (положительные, отрицательные) значения.
отрицательные
11.
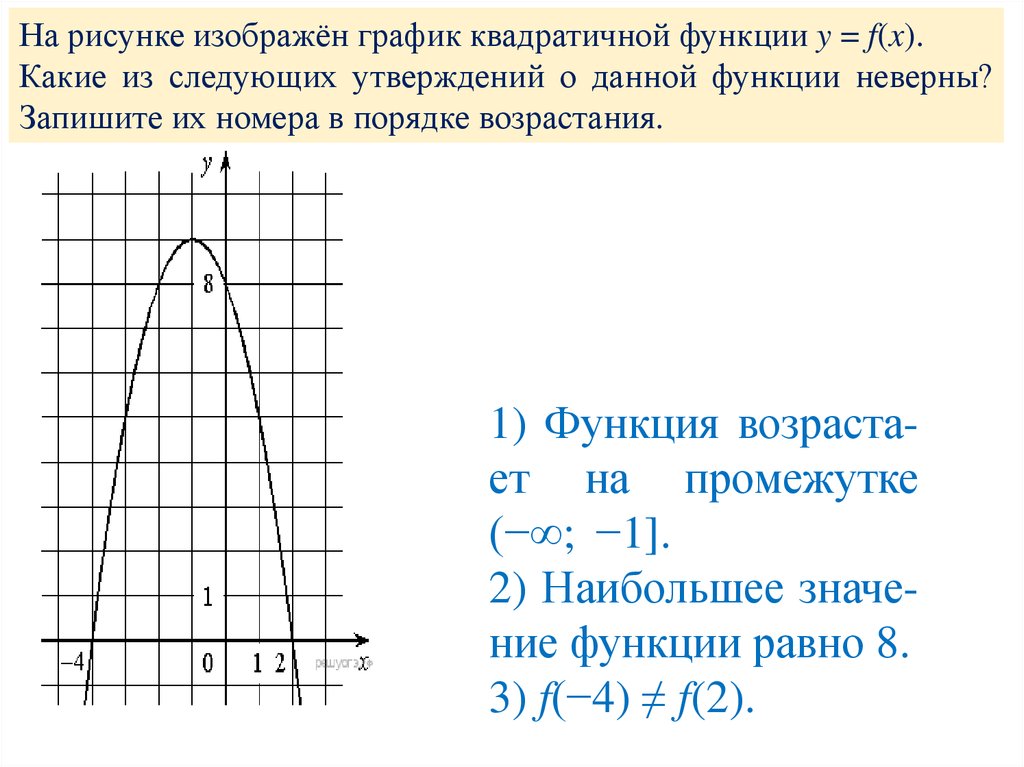
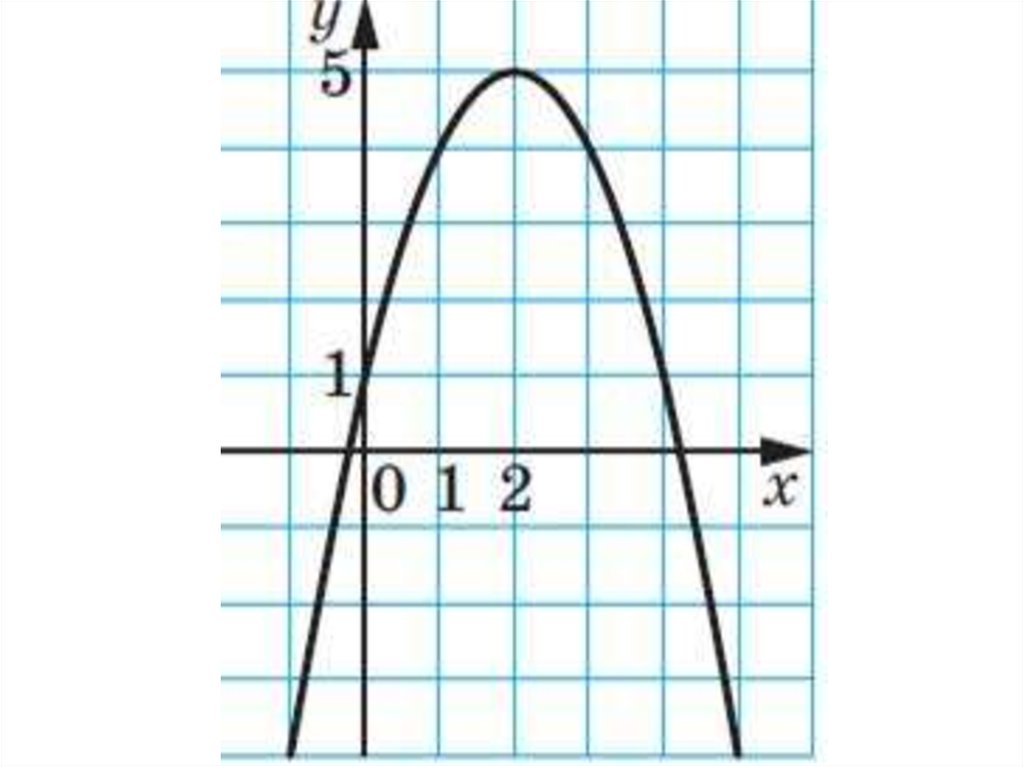
На рисунке изображён график квадратичной функции y = f(x).Какие из следующих утверждений о данной функции неверны?
Запишите их номера в порядке возрастания.
1) Функция возрастает на промежутке
(−∞; −1].
2) Наибольшее значение функции равно 8.
3) f(−4) ≠ f(2).
12.
13.
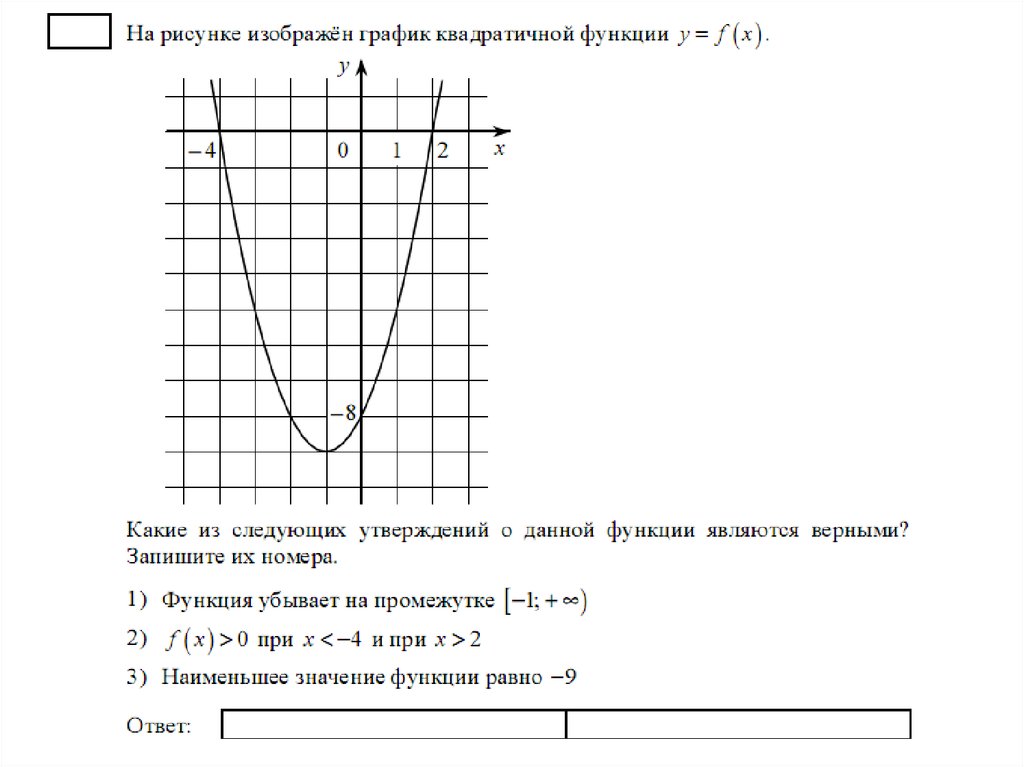
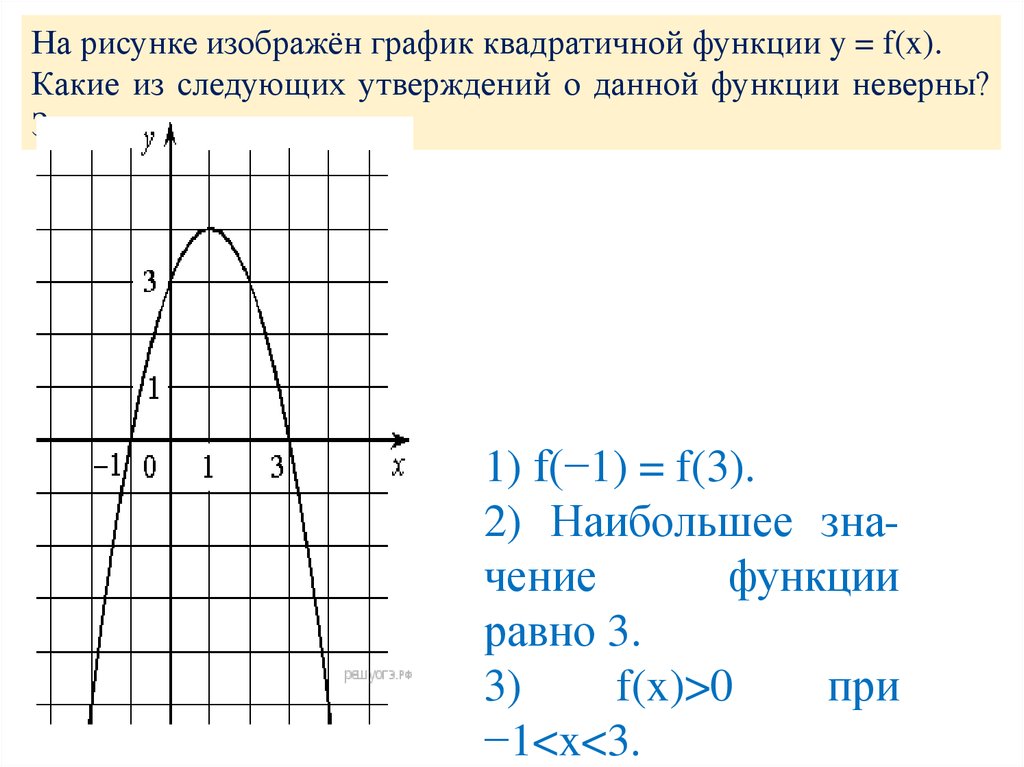
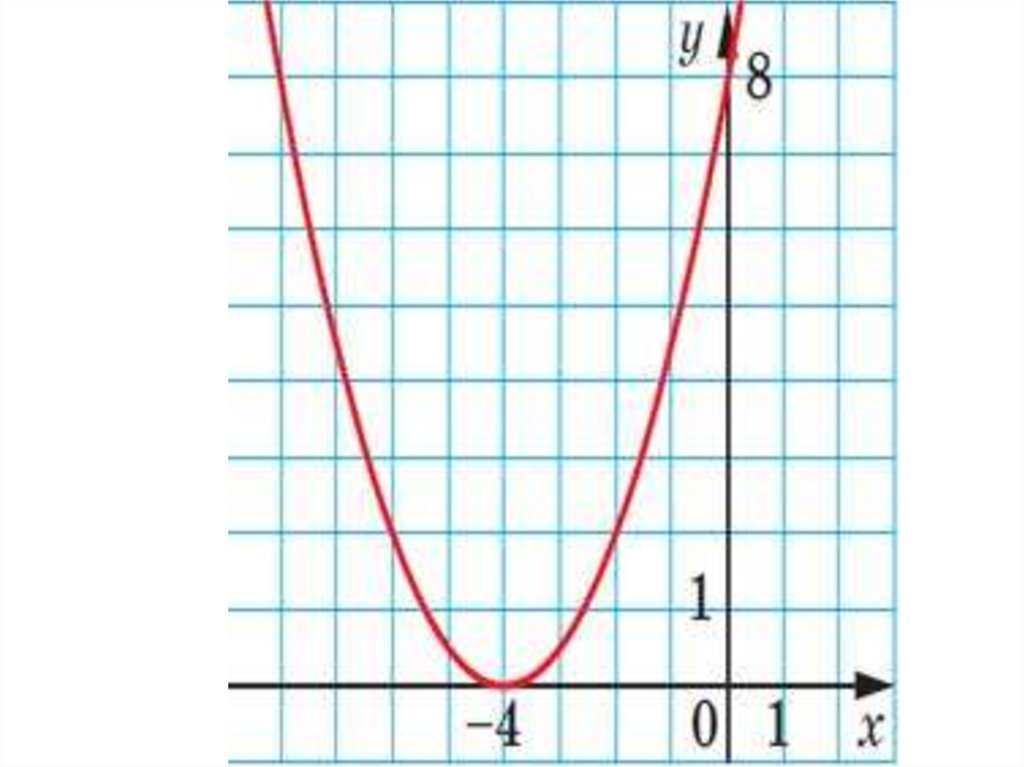
На рисунке изображён график квадратичной функции y = f(x).Какие из следующих утверждений о данной функции неверны?
Запишите их номера.
1) f(−1) = f(3).
2) Наибольшее значение
функции
равно 3.
3)
f(x)>0
при
−1<x<3.
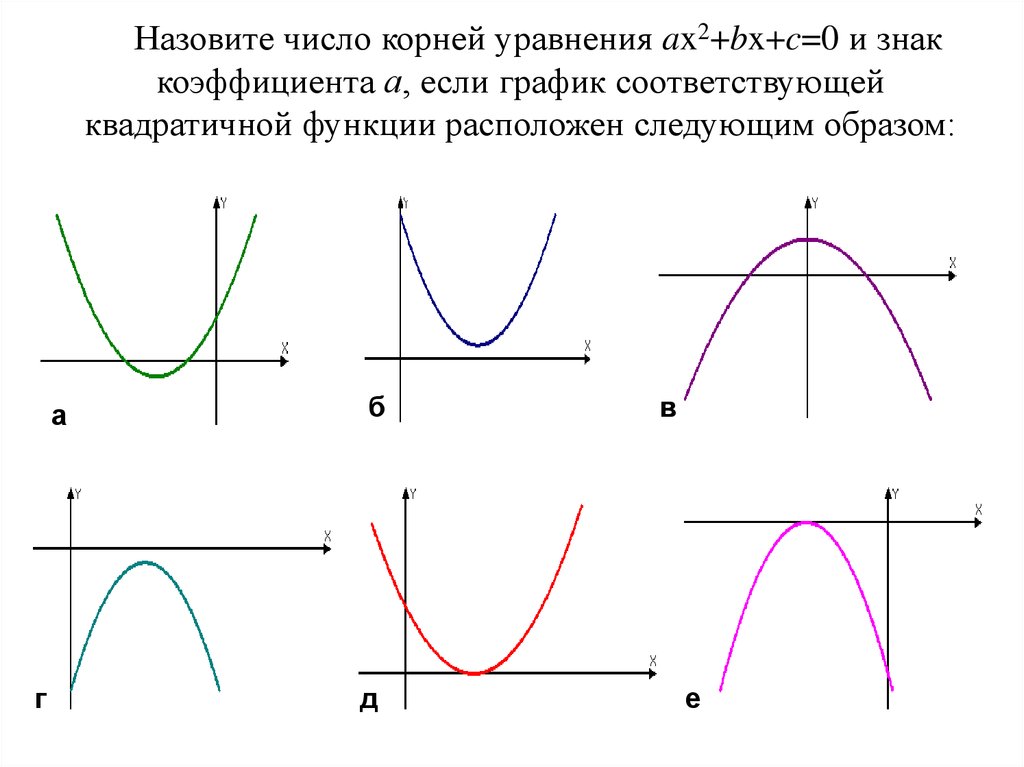
14. Назовите число корней уравнения ax2+bx+c=0 и знак коэффициента а, если график соответствующей квадратичной функции расположен
следующим образом:а
г
б
д
в
е
15.
Преобразования графикаквадратичной функции
Преобразования
графика
Симметрия
Растяжение,
сжатие
Сдвиг
16.
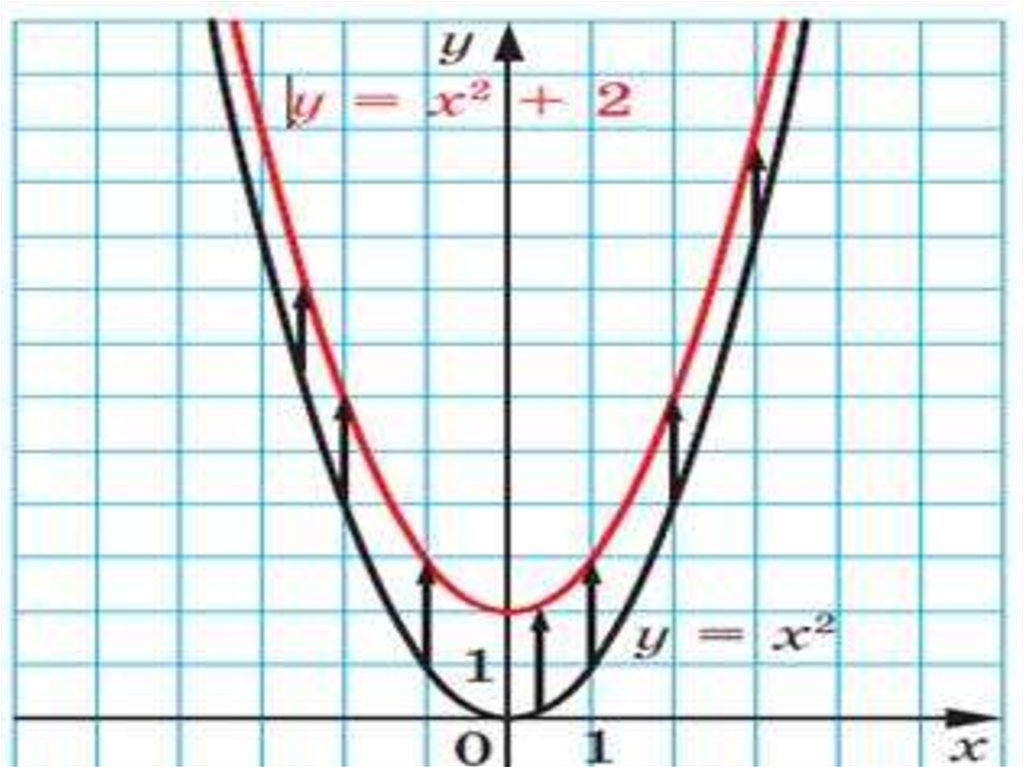
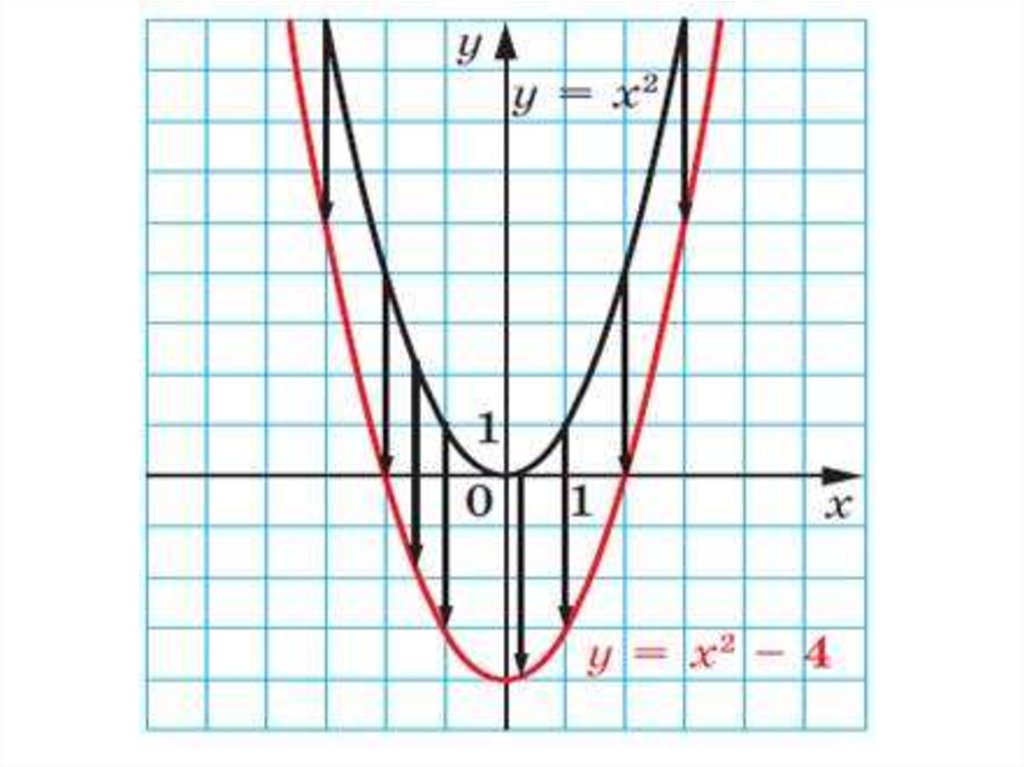
Функция у =ах2+п, ее свойства и график.График функции у=ах2+п является
параболой,
которую
можно
получить из графика функции
у =ах2 с помощью параллельного
переноса вдоль оси у на п единиц
вверх, если п>0, или на –п единиц
вниз, если п<0.
17.
18.
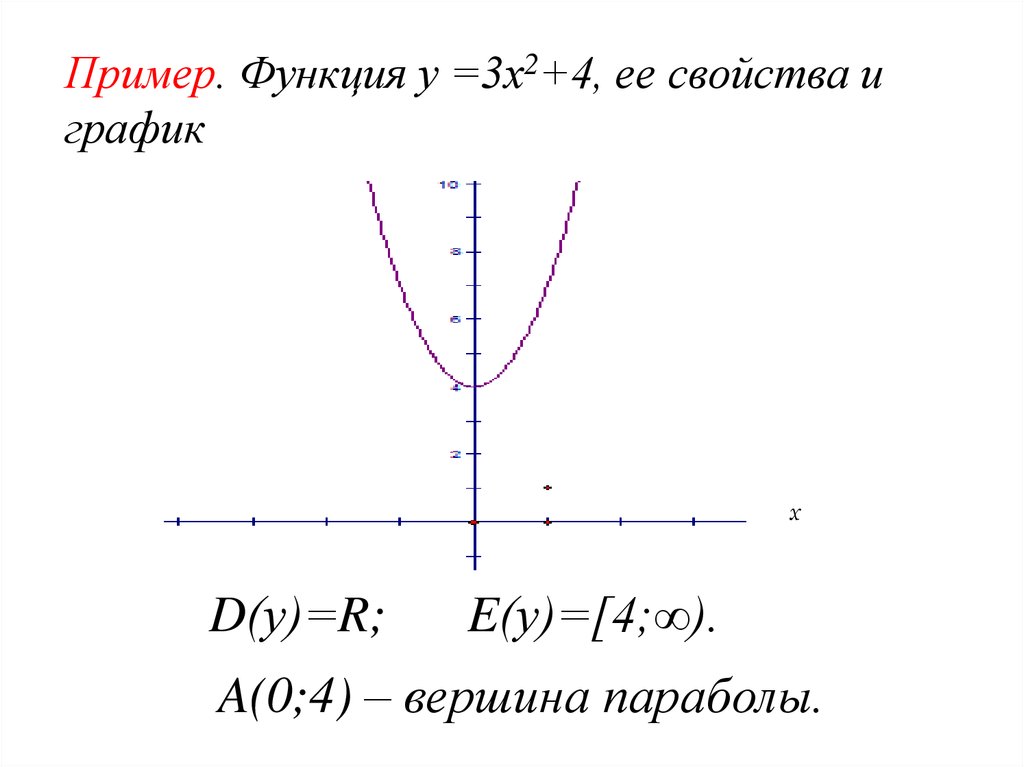
Пример. Функция у =3х2+4, ее свойства играфик
у
А
О
D(у)=R;
х
х
E(у)=[4;∞).
A(0;4) – вершина параболы.
19.
20.
Функция у =-2х2-3, ее свойства и графику
О
В
D(у)=R E(у)=(-∞; -3]
В(0;-3) – вершина параболы
х
у=-
х2-3
21.
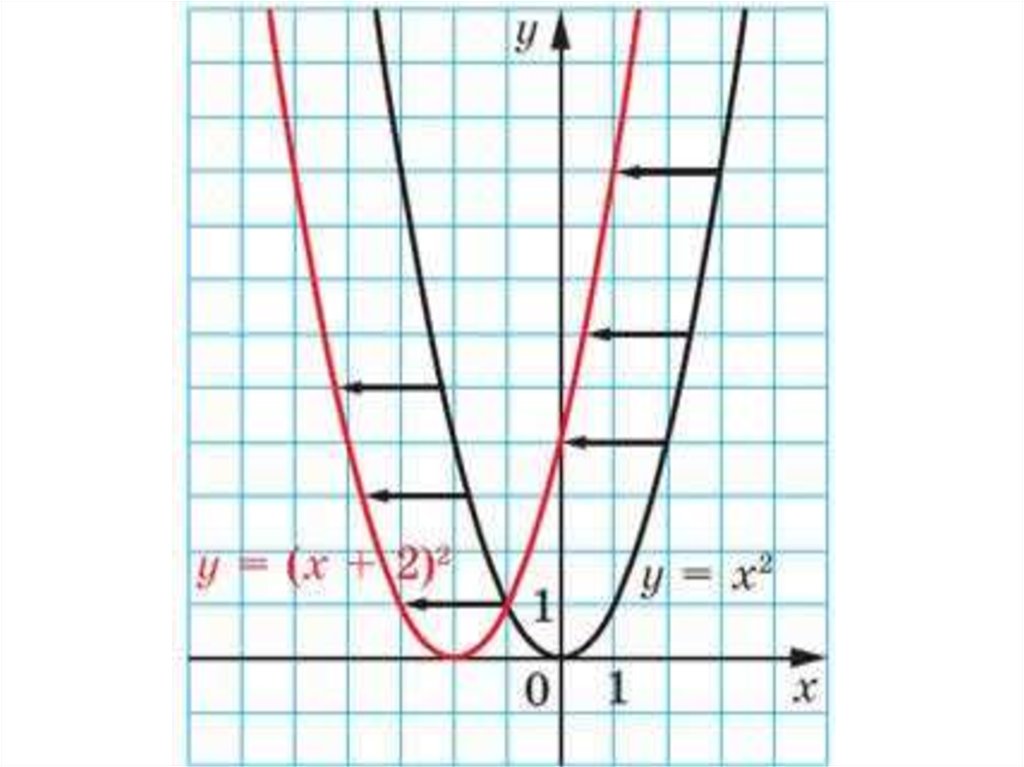
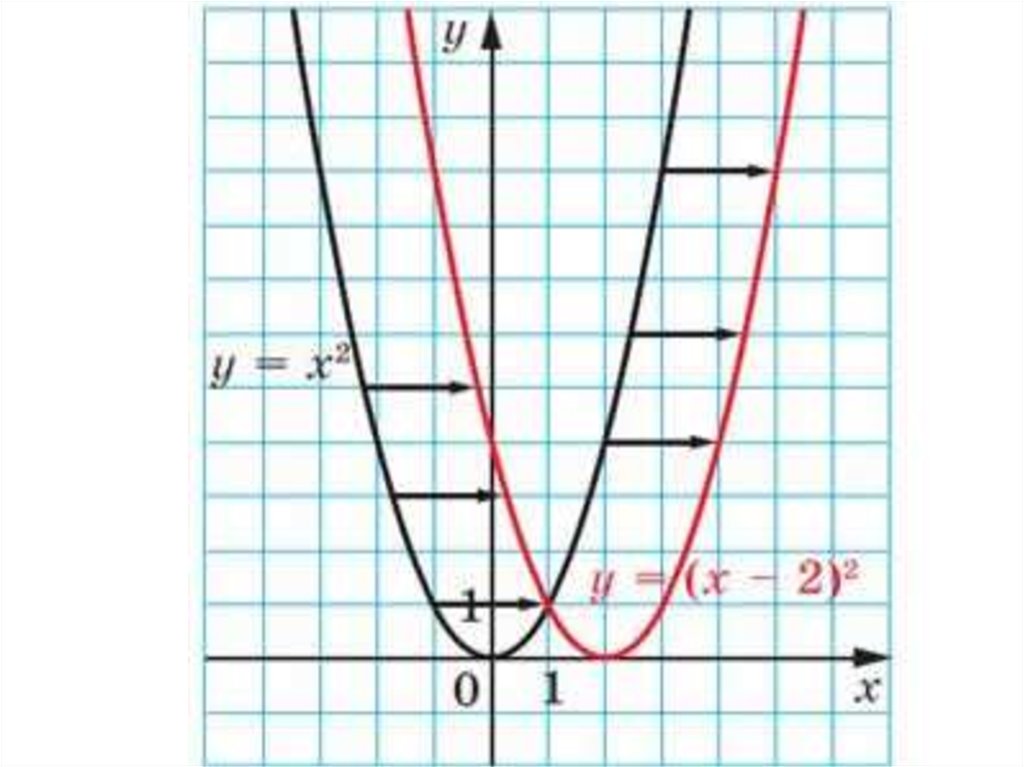
График функции у = а (х - т)2является параболой, которую
можно получить из графика
функции у = ах2 с помощью
параллельного переноса вдоль оси х
на т единиц вправо, если т>0, или
на –т единиц влево, если т<0.
22.
23.
24.
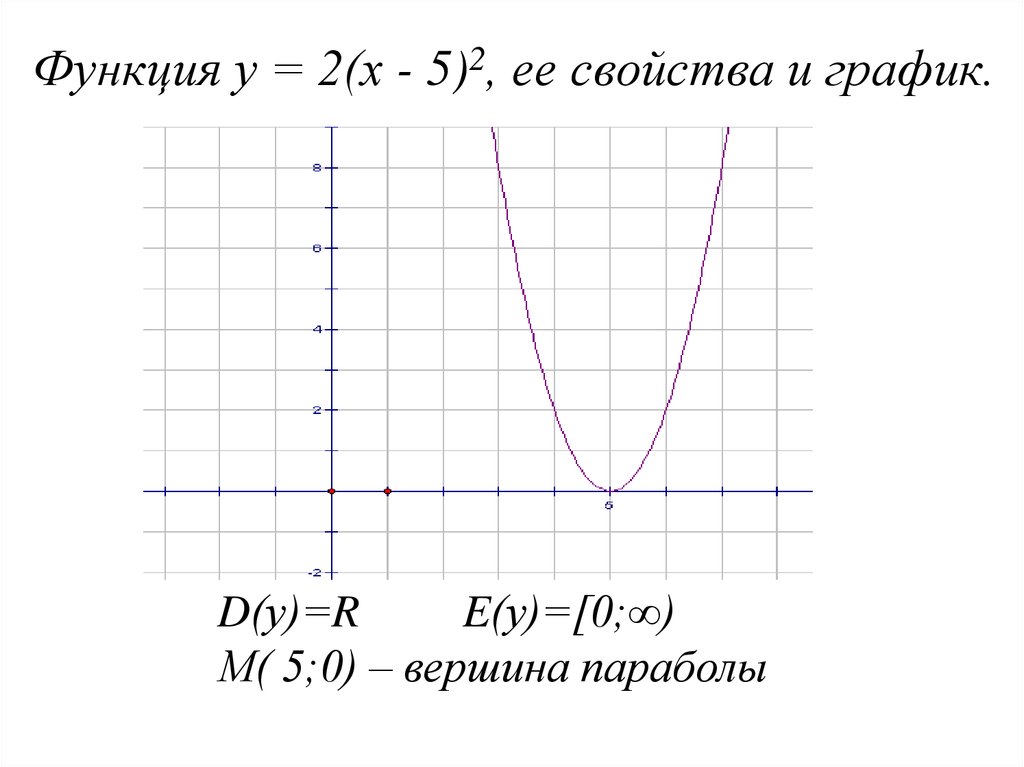
Функция у = 2(х - 5)2, ее свойства и график.у
О
М
D(у)=R
E(у)=[0;∞)
М( 5;0) – вершина параболы
х
25.
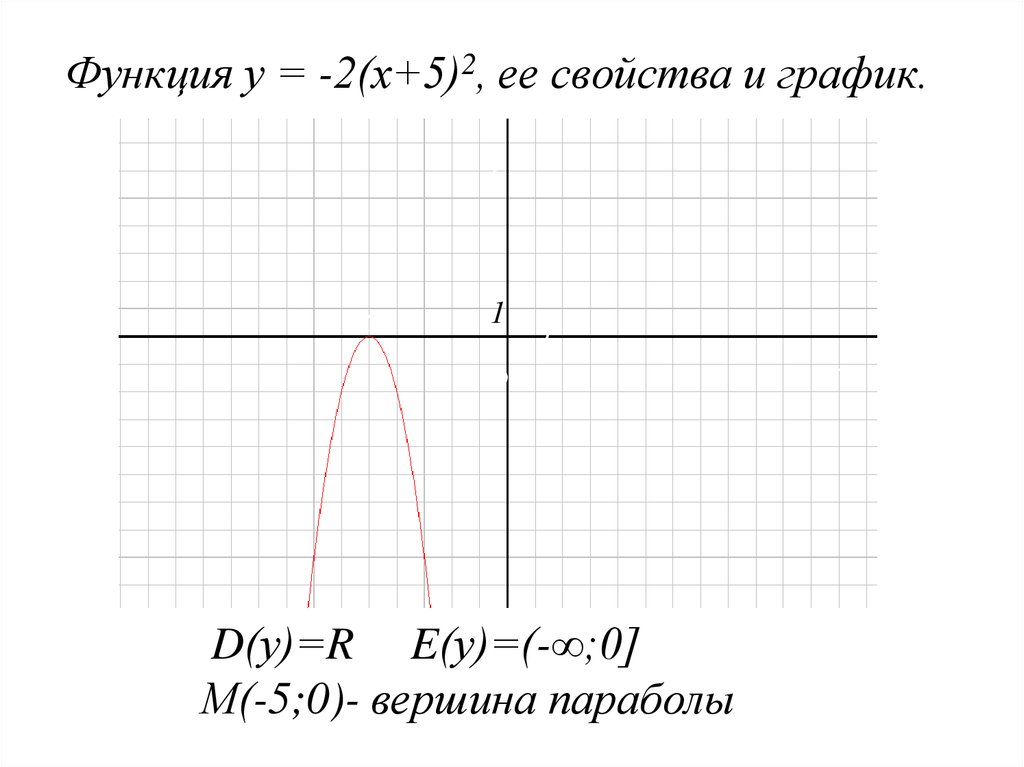
Функция у = -2(х+5)2, ее свойства и график.у
-5
1
1
О
D(у)=R E(у)=(-∞;0]
М(-5;0)- вершина параболы
х
26.
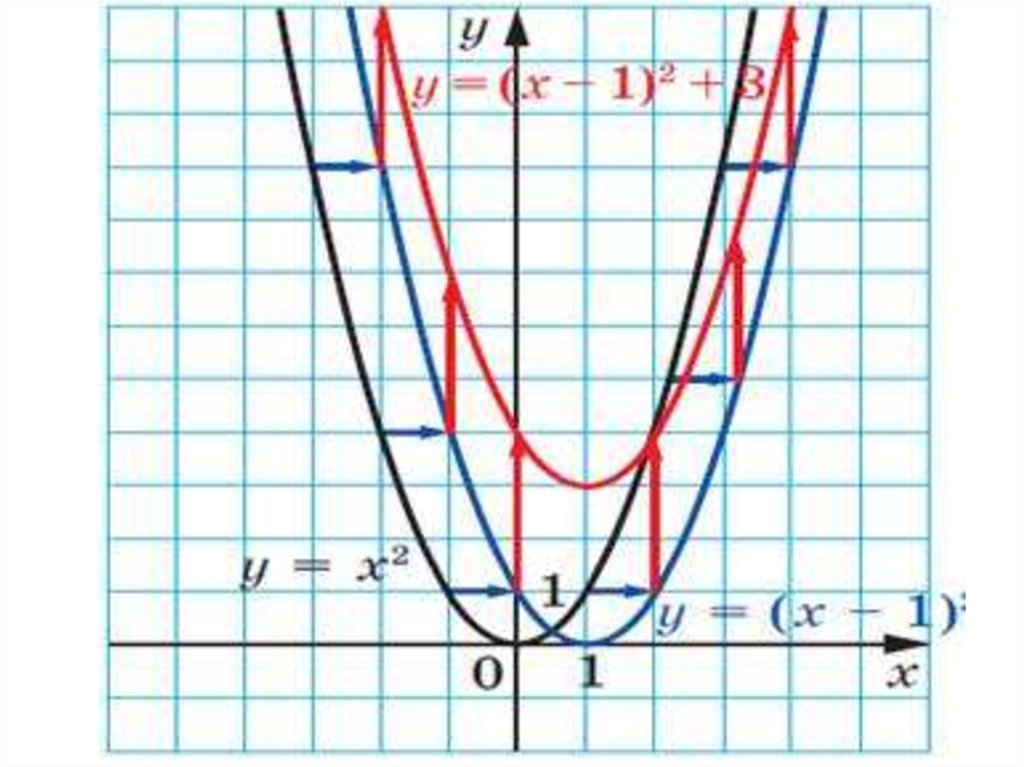
Определение.График функции у = а (х - т)2 + п является
параболой, которую можно получить из
графика функции у = ах2 с помощью двух
параллельных переносов: сдвига вдоль оси
х на т единиц вправо, если т>0, или
на –т единиц влево, если т<0, и сдвига
вдоль оси у на п единиц вверх, если п >0,
или на – п единиц вниз, если п <0.
27.
28.
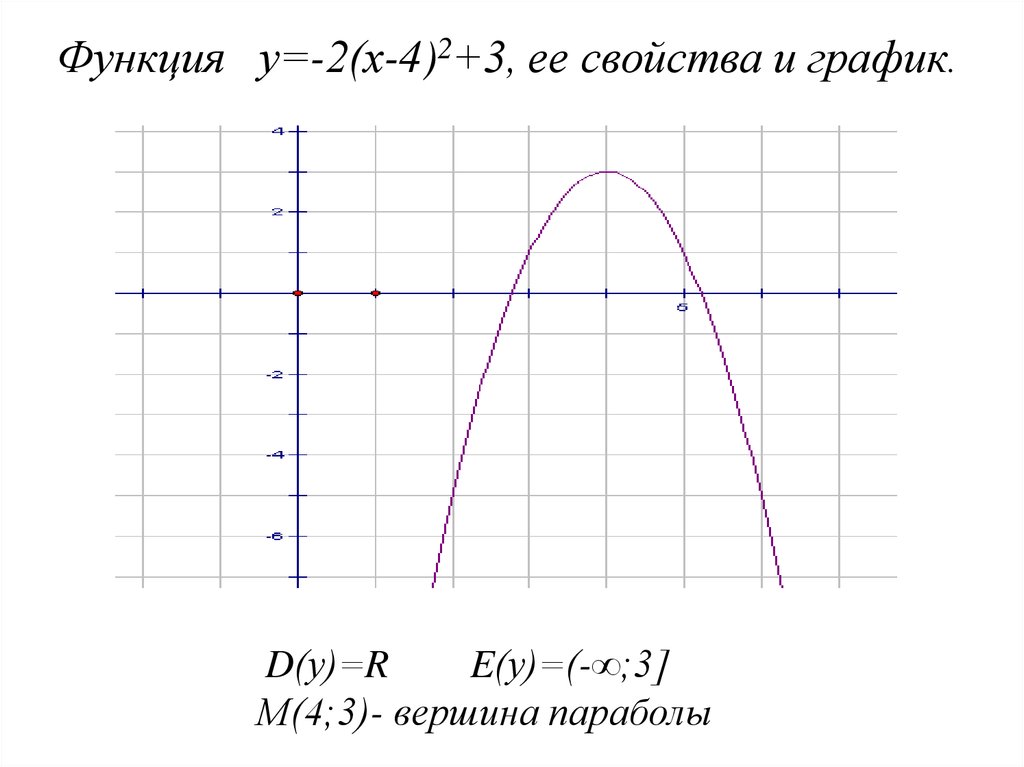
Функция у=-2(х-4)2+3, ее свойства и график.у
М
О
D(у)=R
E(у)=(-∞;3]
М(4;3)- вершина параболы
х
29.
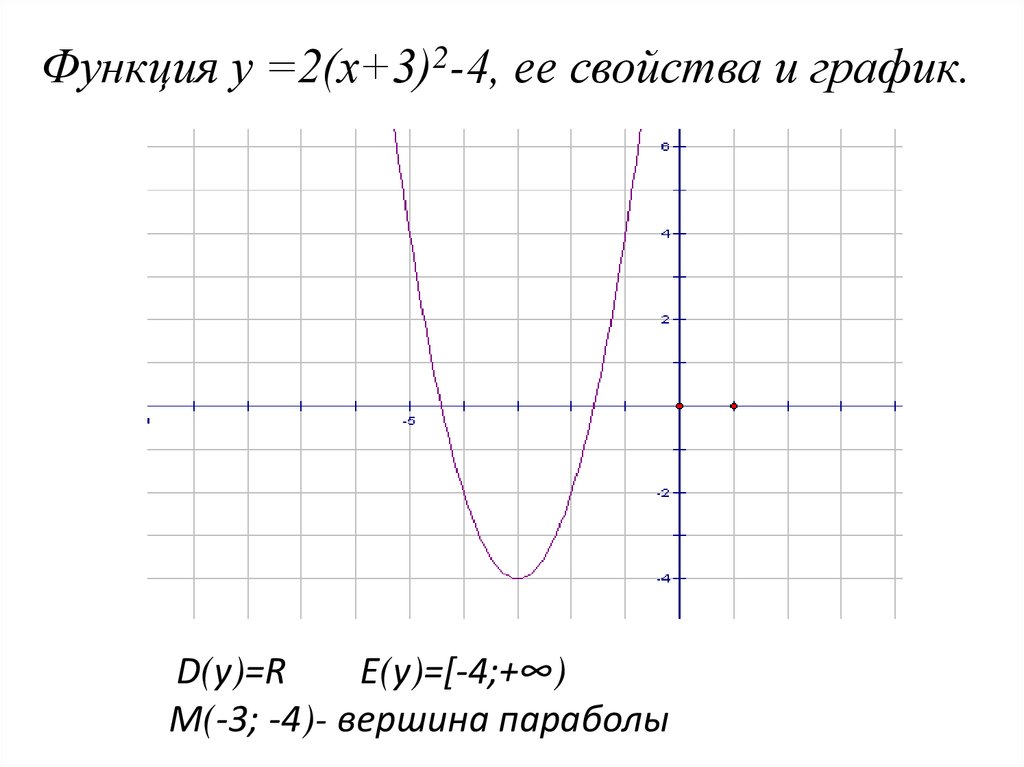
Функция у =2(х+3)2-4, ее свойства и график.у
О
х
М
D(у)=R
E(у)=[-4;+∞)
М(-3; -4)- вершина параболы
30.
12
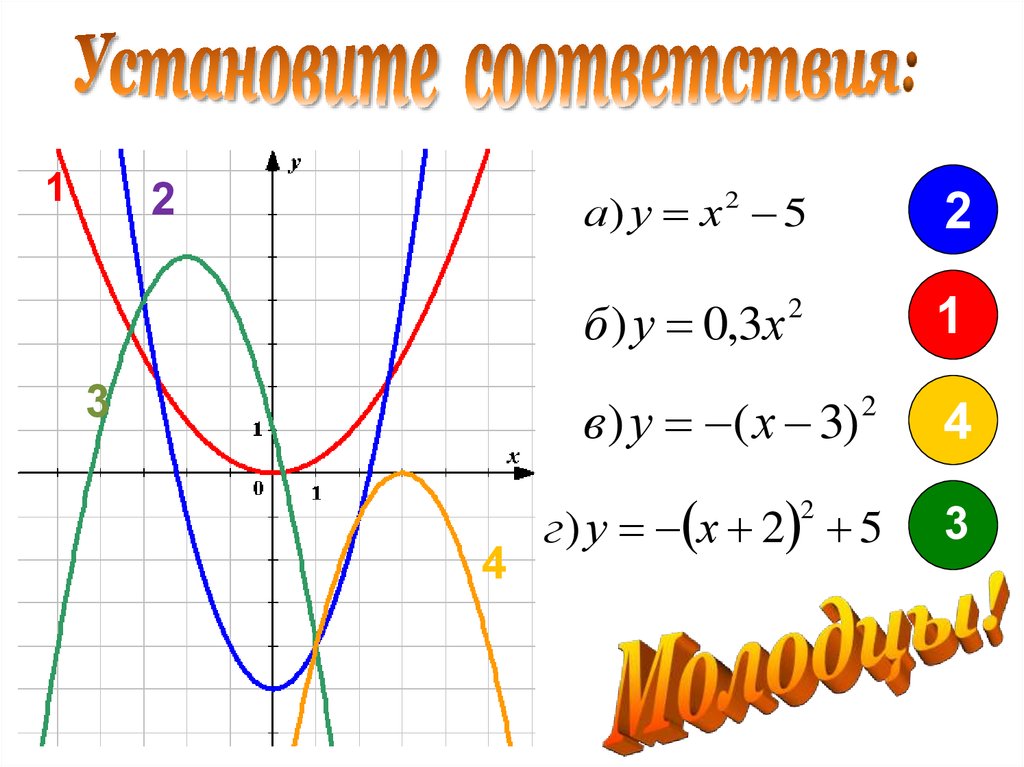
а) у х 5
2
б ) у 0,3х
1
2
3
2
в) у ( х 3)
г ) у х 2 5
2
4
2
4
3
31.
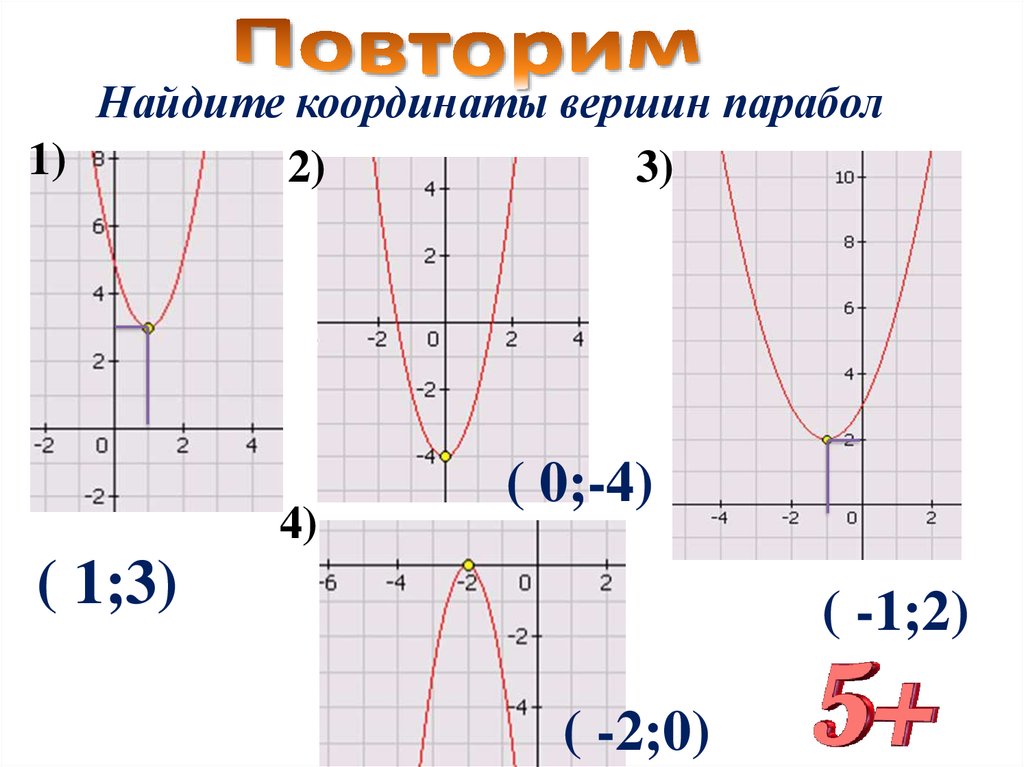
Найдите координаты вершин парабол1)
2)
3)
4)
( 0;-4)
( 1;3)
( -1;2)
( -2;0)









 mathematics
mathematics






