Квадратные неравенства

1. Презентация к уроку Тема «Квадратные неравенства» 9 класс, алгебра Учебник: Алгебра 9 под редакцией Г.В.Дорофеева

Автор: Питимирова Н.А
учитель математики
МКОУ «Чебаклинская СОШ»
Омская область, Большеуковский район, с.Чебаклы

2. Квадратные неравенства

3.

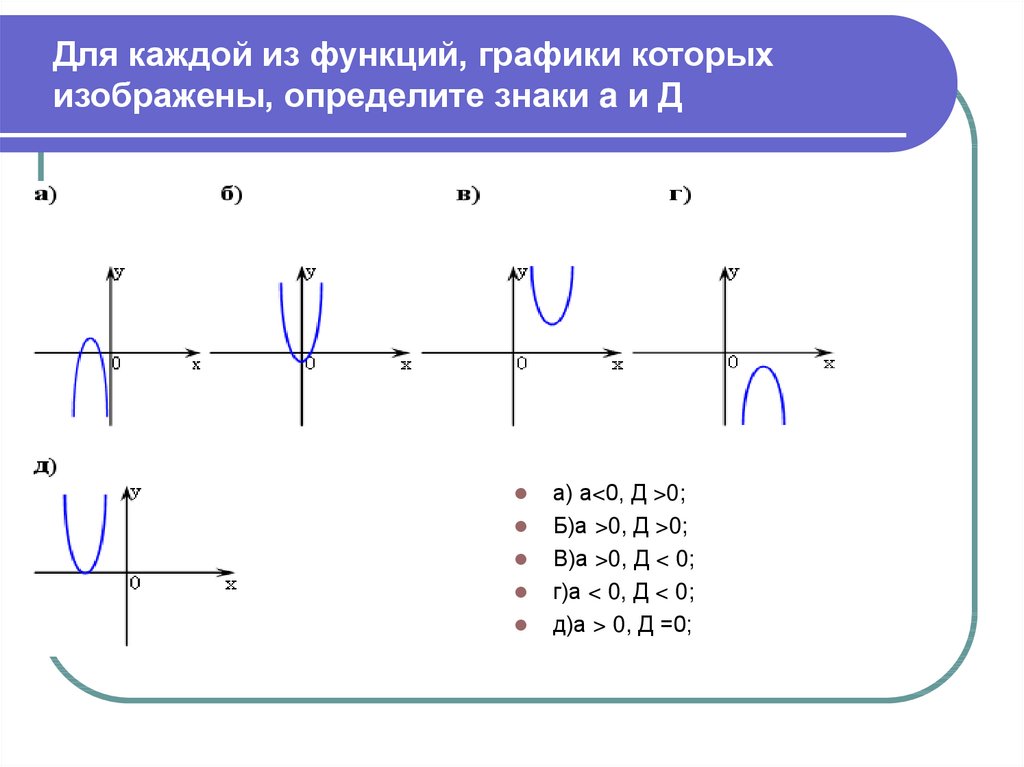
Для каждой из функций, графики которых
изображены, определите знаки a и Д
а) а<0, Д >0;
Б)а >0, Д >0;
В)а >0, Д < 0;
г)а < 0, Д < 0;
д)а > 0, Д =0;

4.   Найдите  значения x, при которых  у>0,  y<0.

Найдите значения x, при которых у>0, y<0.
А) y<0 при любом х (х є R)
Б) y<0 при х≠-1
В) у>0 при х <0 и при х>1, y<0 при 0 < х <1
Г) у< 0 при х <-1 и при х>0, y> 0 при -1 < х<0
д) y> 0 при любом х (х є R)

5.

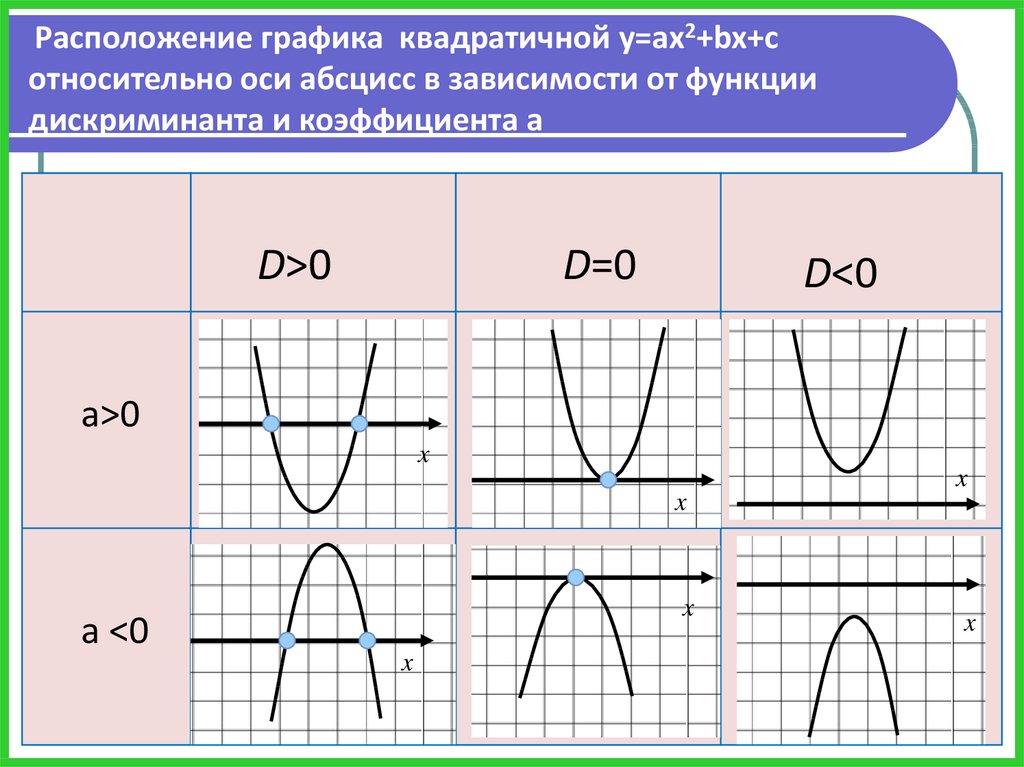
Расположение графика квадратичной у=aх2+bx+c
относительно оси абсцисс в зависимости от функции
дискриминанта и коэффициента а
D>0
D=0
D<0
а>0
x
x
x
x
а <0
x
x

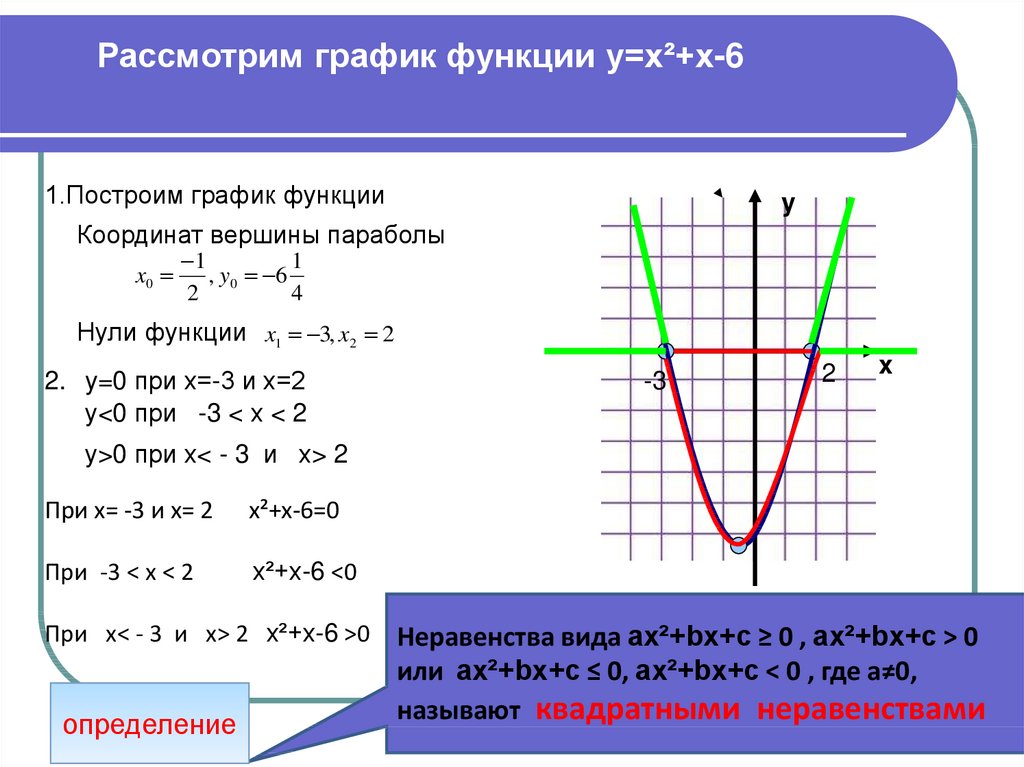
6. Рассмотрим график функции y=x²+x-6

1.Построим график функции
y
Координат вершины параболы
x0
1
1
, y0 6
2
4
Нули функции x1 3, x2 2
2. y=0 при х=-3 и х=2
у<0 при -3 < х < 2
-3
2
x
у>0 при х< - 3 и х> 2
При х= -3 и х= 2
x²+x-6=0
При -3 < х < 2
x²+x-6 <0
При х< - 3 и х> 2 x²+x-6 >0
определение
Неравенства вида ax²+bx+c ≥ 0 , ax²+bx+c > 0
или ax²+bx+c ≤ 0, ax²+bx+c < 0 , где а≠0,
называют квадратными неравенствами

7. Алгоритм решения квадратного неравенства

Рассмотреть функцию у=ах2 + bx +c
1.Найти нули функции (решить уравнение
ах2 + bx +c=0)
2.Определить направление ветвей параболы
3.Схематично построить график функции.
4.Учитывая знак неравенства, выписать ответ.

8.

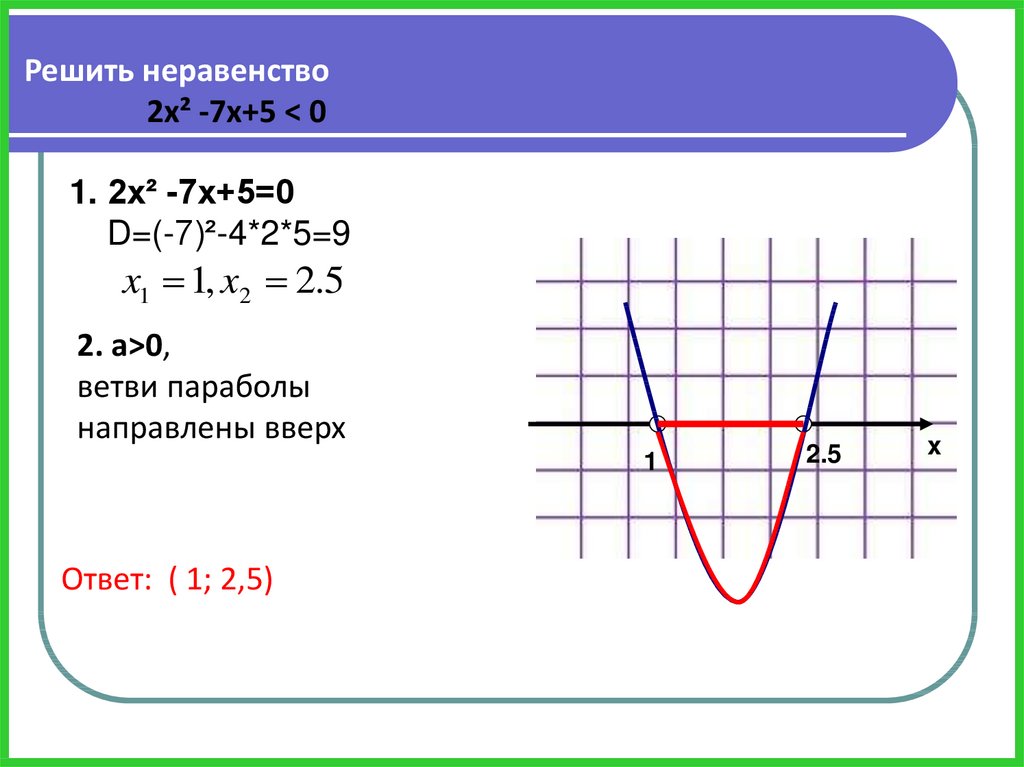
Решить неравенство
2х² -7х+5 < 0
1. 2х² -7х+5=0
D=(-7)²-4*2*5=9
x1 1, x2 2.5
2. а>0,
ветви параболы
направлены вверх
1
Ответ: ( 1; 2,5)
2.5
x

9. Решите неравенство

а) x² -2x -3 >0
Ответ:(-∞ ; -1 ) U ( 3 +∞)
б) x² -2x -3 ≥ 0
Ответ:(-∞ ; -1 ] U [ 3 +∞)
в) x² -2x -3 < 0
Ответ:( -1; 3 )
г) x² -2x -3 ≤ 0
Ответ:[ -1; 3 ]
-1
3
х

10.

Решить неравенство
- 4х2+2х≥0
2
1. -4x +2х=0
2
4х -2х=0
2х(2х -1) =0
Х1 =0
х2 =0,5
2. а <0
Ветви направлены вниз
Ответ:[ 0 ; 0,5 ]
0
0,5

11.

Решить неравенство
1) х² +4≥0
1. х² +4 =0
х² = -4, корней нет
2.а>0, ветви параболы
направлены вверх
Ответ:(-∞ ; +∞)
2) х² +4 < 0
Ответ: {Ǿ}

12.

Решить неравенство
а)
( x 2) 2 0
1 ( x 2) 0, x 2
2. а <0,
ветви направлены вниз
2
Ответ: Х =2
б) ( x 2) 2 0
Ответ: {Ǿ}
в) ( x 2) 2 0
Ответ: х≠2
г) ( x 2) 2 0
Ответ:(-∞ ; +∞)
2

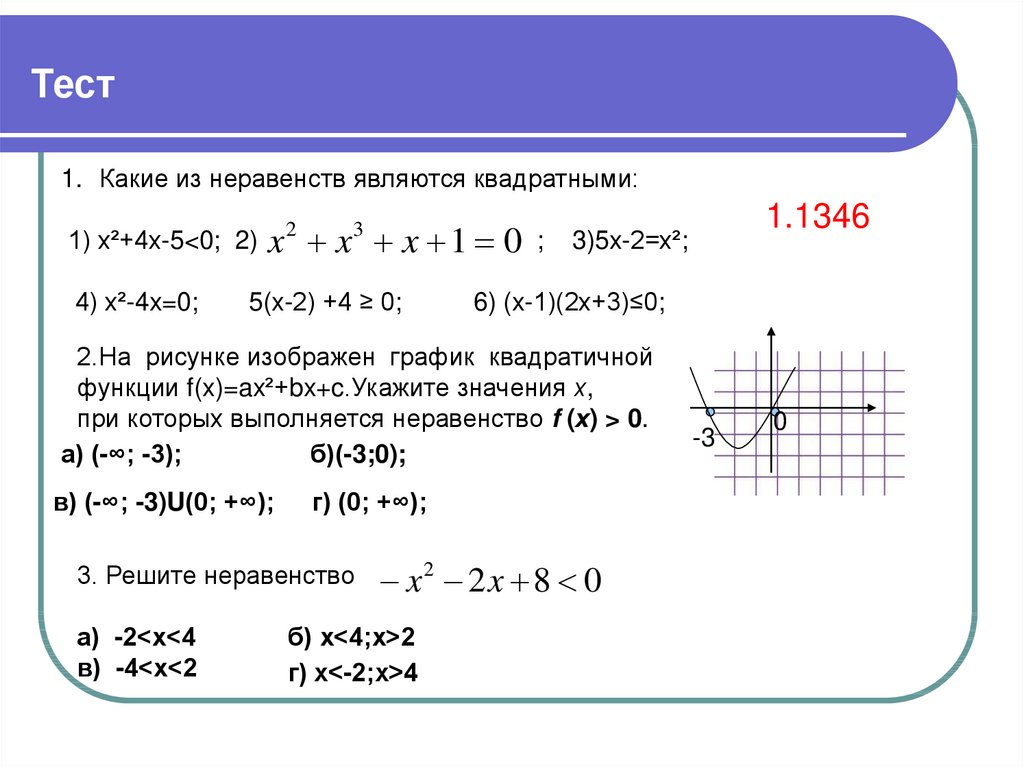
13. Тест

1. Какие из неравенств являются квадратными:
1) x²+4x-5<0; 2)
4) x²-4x=0;
x x x 1 0
2
3
5(x-2) +4 ≥ 0;
;
6) (x-1)(2x+3)≤0;
2.На рисунке изображен график квадратичной
функции f(x)=ax²+bx+c.Укажите значения х,
при которых выполняется неравенство f (х) > 0.
а) (-∞; -3);
б)(-3;0);
в) (-∞; -3)U(0; +∞);
г) (0; +∞);
3. Решите неравенство
а) -2<х<4
в) -4<х<2
x2 2x 8 0
б) х<4;х>2
г) х<-2;х>4
1.1346
3)5x-2=x²;
-3
0

14. Домашнее задание

П 2.5
№289,
№292(а,в)
№294(а,в)

15. Литература:

Учебник: Алгебра 9 класс под редакцией Г.В.Дорофеева Москва
«Просвещение» 2011г
2.Петров К. Квадратичная функция и её применение: Кн.для учащихся.- М.:
Просвещение, 1995.
3.Математика.9 класс. Подготовка к ГИА – 2012.Учебно – методическое
пособие /Под ред. Ф.Ф. Лысенко, С.Ю. Кулабухова. -Ростов – на – Дону:
Легион – М, 2011.
1.