4.15M

Category: $mathematics$ mathematics

Диаграммы Венна. Операции над множествами

1.

Конспект лекций по дисциплине «Дискретная математика»
лектор – Гонтовая Наталия Викторовна
ГОУ ВПО ЛНР «Донбасский государственный технический университет»
2015-2016 учебный год
Тема 3:
Диаграммы Венна.
Операции над
множествами.
ДМ, лектор – Гонтовая Н.В.

2.

стр.2
ПЛАН к теме 3:
1. Логические диаграммы. Диаграммы Венна
2. Операции над множествами. Свойства операций
3. Законы алгебры множеств
3.1 Законы де Моргана
3.2 Закон поглощения
3.3 Закон склеивания
4. Примеры решения задач по теме 3
5. Задания на самопроработку по теме 3
БЛОК 3.1
ДМ, лектор – Гонтовая Н.В.

3.

стр.3
1
Логические диаграммы (ЛД) – графический аппарат
теории множеств и математической логики.
Разновидностями логических диаграмм являются
диаграммы Эйлера, диаграммы Венна, диаграммы Вейча,
карты Карно и др.
Идея ЛД известна, начиная со средних веков.
Графические способы представления множеств
использовались в работах таких ученых как
Г.В. Лейбниц, Л. Эйлер, Э. Шрёдер, Ч.Л. Доджсон,
Дж. Вэнн и др.
ДМ, лектор – Гонтовая Н.В.

4.

стр.4
Готфрид Вильгельм Лейбниц (1646-1716) – немецкий
математик-логик-физик-философ-языковед-юрист-дипломат
Леонард Эйлер (1707-1783) – математик-физик-механикастроном. Эйлер впервые подробно и обоснованно
изложил идею использования ЛД («круги Эйлера»)
«Л. Эйлер. Письма … к немецкой принцессе (1768 г.)»
Эрнст Шрёдер (1841-1902) – немецкий математик-логик
ДМ, лектор – Гонтовая Н.В.

5.

стр.5
Чарлз Лютвидж Доджсон (1832-1898) – он же
Льюис Кэррол («Алиса в стране чудес») – английский
математик-логик-писатель, автор логических парадоксов.
Доджсон разработал удобную графическую технику решения
логических задач.
«Ч.Л.Доджсон. Символическая логика»
«Ч.Л.Доджсон. Логическая игра»
Доджсон сформулировал общие правила и алгоритмы для
получения правильного вывода из суждений, лишенных, на
первый взгляд, здравого смысла. Особого мастерства
достиг в составлении, анализе и решении таких логических
задач как «силлогизмы» и «сориты».
???
ДМ, лектор – Гонтовая Н.В.

6.

стр.6
Джон Венн (1834 – 1923) – английский математик-логик
Диграммы Венна (разновидность логических диаграмм) –
способ схематического представления множеств и
операций над множествами.
Диаграммы Венна используются при решении любых
логических задач, в том числе для иллюстрации
логических высказываний в булевой алгебре, находят
применение в приложениях математической логики и
теории автоматов, в частности при решении задач,
связанных с использованием нейронных цепей.
Диаграммы Венна (ДВ) представляются в виде замкнутых
кривых (как правило, – кругов), ограничивающих области,
которым ставятся в соответствие те или иные множества.
ДМ, лектор – Гонтовая Н.В.

7.

стр.7
На диаграммах Венна можно продемонстрировать
сходство, различия и взаимосвязи между понятиями,
категориями, группами и др. объектами, представленными
в виде множеств.
При этом сходство между отдельными множествами
(общие элементы множеств) представляется на ДВ
перекрывающимися частями кругов, а различия –
неперекрывающимся частями кругов.
Если множества не имеют общих элементов, то их
изображают на ДВ непересекающимися кругами.
На ДВ универсальное множество (…) изображают в виде
прямоугольника.
ДМ, лектор – Гонтовая Н.В.

8.

стр.8
U - универсум
U
C
B
ДМ, лектор – Гонтовая Н.В.

9.

стр.9
1 2 3 4 5 6
ДМ, лектор – Гонтовая Н.В.

10.

см. Тема 2, п.9
стр.10
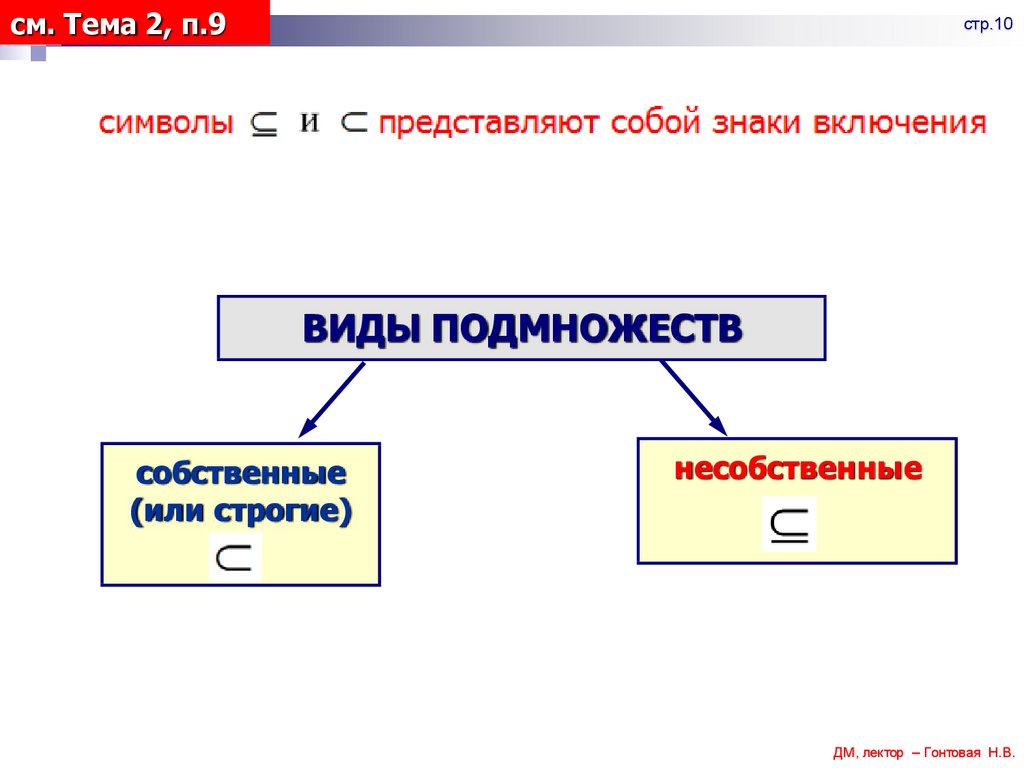
ВИДЫ ПОДМНОЖЕСТВ
собственные
(или строгие)
несобственные
ДМ, лектор – Гонтовая Н.В.

11.

см. Тема 2, п.9
стр.11
Множество В называют собственным подмножеством множества
при следующих условиях:
А
при этом множество А содержит хотя бы один элемент,
не принадлежащий подмножеству В.
Форма записи собственных подмножеств:
Говорят: «множество В строго включено в множество А»
Если множество В является собственным подмножеством множества А,
то мощность множества В меньше мощности множества А:
ДМ, лектор – Гонтовая Н.В.

12.

см. Тема 2, п.9
стр.12
Подмножество В называют несобственным подмножеством
множества
А
при следующих условиях:
Форма записи несобственных подмножеств:
!!! Запись
более конкретна, чем
Записывая
, мы гарантируем, что
тогда как запись
.
,
не исключает случая
ДМ, лектор – Гонтовая Н.В.

13.

стр.13
Примеры диаграмм Венна – см. рисунок 1, 2, 3.
!!! При всей своей наглядности, диаграммы Венна являются
всего лишь иллюстрацией (визуализацией) взаимного
соотношения множеств, но не могут использоваться в
качестве инструмента строгого формального
доказательства логических выводов.
ДМ, лектор – Гонтовая Н.В.

14.

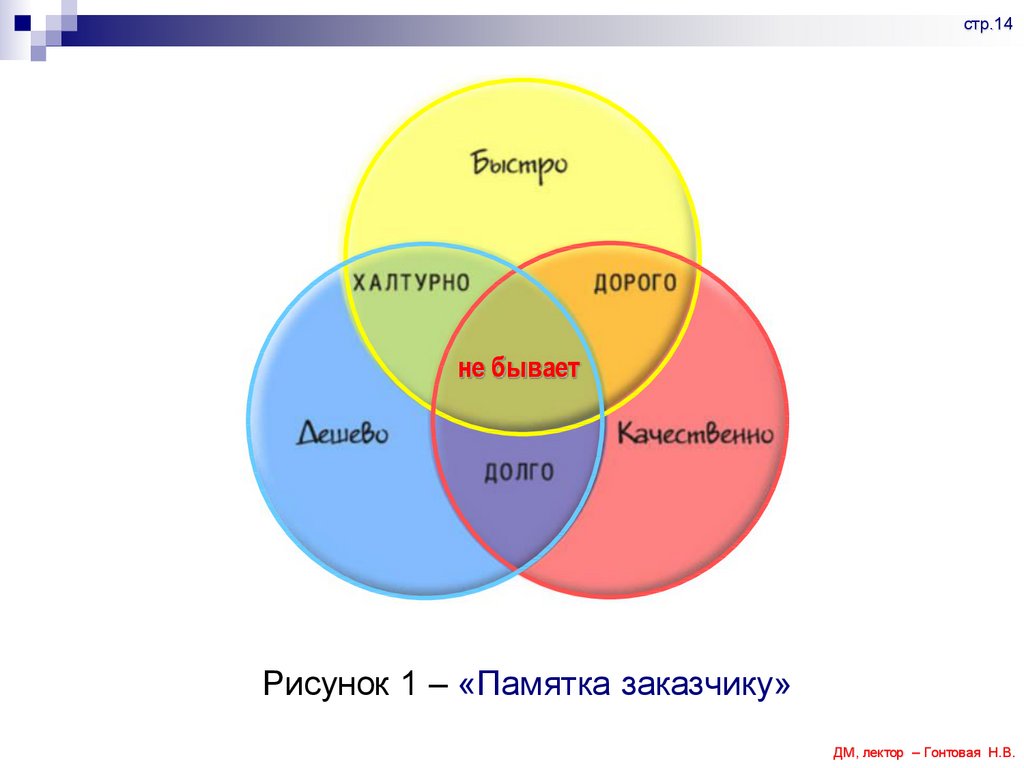
стр.14
не бывает
Рисунок 1 – «Памятка заказчику»
ДМ, лектор – Гонтовая Н.В.

15.

стр.15
Рисунок 2 – Представления И. Канта о формах государства
ДМ, лектор – Гонтовая Н.В.

16.

стр.16
Греческий
Латинский
Русский
Рисунок 3 – Что общего у русского, греческого и латинского
алфавитов (заглавные буквы)?
ДМ, лектор – Гонтовая Н.В.

17.

стр.17
Греческий алфавит:
ДМ, лектор – Гонтовая Н.В.

18.

стр.18
Инструменты рисования диаграмм Венна:
1
Создание диаграммы Венна с помощью
Gliffy
Gliffy – онлайн-программа для создания схем, графиков,
планов помещений, диаграмм (в том числе Venn diagrams,
BPMN, UML, UI Design, SWOT и др).
Запустить приложение можно без установки, просто зайти
на сайт
www.gliffy.com
Высокий уровень функционала при работе в Gliffy
достигается благодаря использованию Flash-технологии.
http://fevt.ru/load/gliffy_diagrams/104-1-0-839
ДМ, лектор – Гонтовая Н.В.

19.

стр.19
2
Создание диаграммы Венна с помощью приложения
Office (в виде графического элемента SmartArt
на основе макета диаграмм Венна)
https://support.office.com
ДМ, лектор – Гонтовая Н.В.

20.

стр.20
ДМ, лектор – Гонтовая Н.В.

21.

2
стр.21
Операции над множествами – это процедуры, с помощью
которых из заданных множеств можно сконструировать
новые множества (или другими словами – это способы
конструирования новых множеств на основе заданных
множеств).
ДМ, лектор – Гонтовая Н.В.

22.

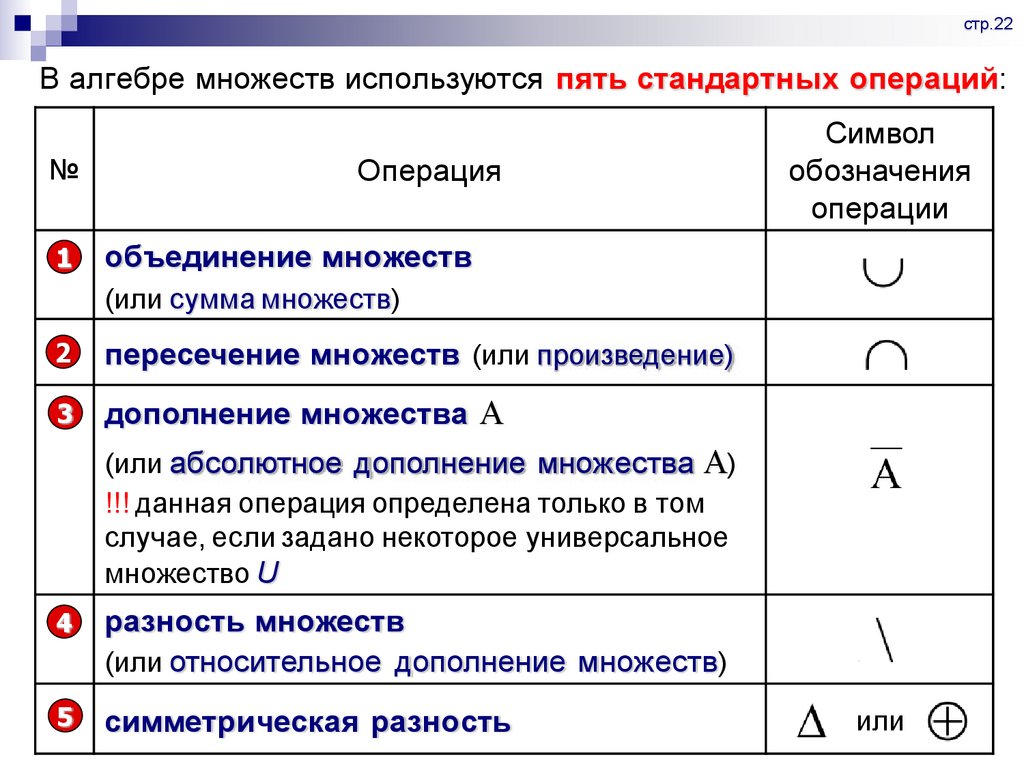
стр.22
В алгебре множеств используются пять стандартных операций:
№
1
Операция
Символ
обозначения
операции
объединение множеств
(или сумма множеств)
2
пересечение множеств (или произведение)
3
3
дополнение множества А
(или абсолютное дополнение множества А)
!!! данная операция определена только в том
случае, если задано некоторое универсальное
множество U
4
разность множеств
(или относительное дополнение множеств)
5
симметрическая разность
или

23.

Операция
стр.23
1
Объединением (или суммой) множеств
А и В называется
х таких, что х принадлежит хотя бы
одному из 2-х множеств А или В :
множество элементов
В общем случае, объединением n множеств
называется множество , состоящее из элементов, входящих
хотя бы в одно из этих n множеств :
где
– обозначение логической операции «ИЛИ»
ДМ, лектор – Гонтовая Н.В.

24.

стр.24
Пример 1:
Операция объединения множеств:
ДМ, лектор – Гонтовая Н.В.

25.

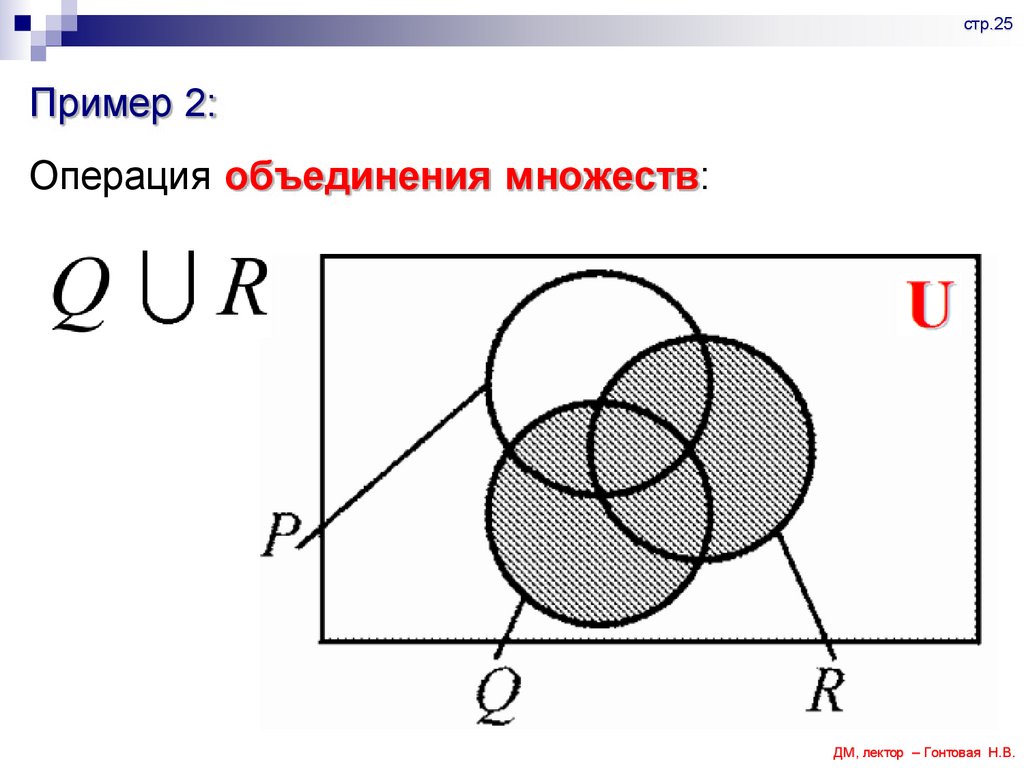
стр.25
Пример 2:
Операция объединения множеств:
ДМ, лектор – Гонтовая Н.В.

26.

стр.26
Свойства операции объединения множеств:
1) Объединение множеств коммутативно
(свойство коммутативности объединения множеств)
ДМ, лектор – Гонтовая Н.В.

27.

стр.27
2) Объединение множеств ассоциативно
(свойство ассоциативности объединения множеств)
а значит, при записи нескольких множеств,
соединённых знаком операции объединения,
скобки можно не использовать.
ДМ, лектор – Гонтовая Н.В.

28.

стр.28
3) Если
или
, то
ДМ, лектор – Гонтовая Н.В.

29.

стр.29
Следствия из свойства 3 :
ДМ, лектор – Гонтовая Н.В.

30.

стр.30
4)* Дистрибутивность объединения множеств
относительно пересечения этих множеств
(или свойство дистрибутивности …)
Дистрибутивный (от лат.«distributivus» – распределительный)
!!! Благодаря свойству дистрибутивности можно раскрывать
скобки в сложных выражениях.
ДМ, лектор – Гонтовая Н.В.

31.

Операция
стр.31
2
А и В
называется множество элементов х таких, что х принадлежит
и множеству А, и множеству В :
Пересечением (или произведением) множеств
Пересечением (или произведением)
n
множеств
называется множество
которого принадлежит каждому из этих
где
, каждый элемент
n множеств:
– обозначение логической операции «И»
ДМ, лектор – Гонтовая Н.В.

32.

стр.32
Например:
Операция пересечения множеств:
ДМ, лектор – Гонтовая Н.В.

33.

стр.33
Свойства операции пересечения множеств:
1) Пересечение множеств коммутативно
(свойство коммутативности пересечения множеств)
ДМ, лектор – Гонтовая Н.В.

34.

стр.34
2) Пересечение множеств ассоциативно
(свойство ассоциативности пересечения множеств)
а значит, при записи нескольких множеств,
соединённых знаком операции пересечения,
скобки можно не использовать.
ДМ, лектор – Гонтовая Н.В.

35.

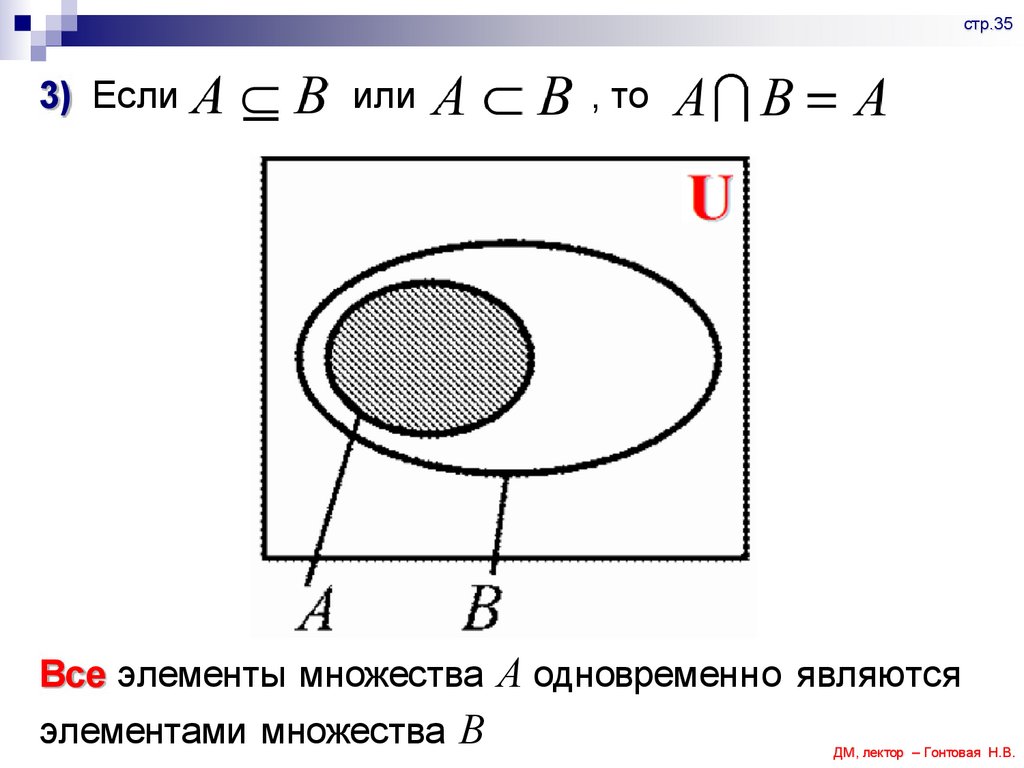
стр.35
3) Если
или
, то
Все элементы множества А одновременно являются
элементами множества В
ДМ, лектор – Гонтовая Н.В.

36.

стр.36
Следствия из свойства 3 :
ДМ, лектор – Гонтовая Н.В.

37.

стр.37
4)* Дистрибутивность пересечения относительно
объединения (или свойство дистрибутивности …)
!!! Не путать со свойством:
Дистрибутивность объединения относительно
пересечения
ДМ, лектор – Гонтовая Н.В.

38.

стр.38
5)* Дистрибутивность пересечения множеств
относительно симметрической разности
(или свойство дистрибутивности …)
Контроль:
Дистрибутивный (от лат.« … » – … )
!!! Благодаря свойству дистрибутивности можно … в сложных
выражениях.
ДМ, лектор – Гонтовая Н.В.

39.

стр.39
!!! Приоритет выполнения операций:
если в выражении встречаются операции
и
то первой выполняется операция пересечения множеств
а затем – операция объединения множеств
.
,
Благодаря такому соглашению многие формулы
допускается записывать без скобок, и использовать их
только в тех случаях, когда порядок действий
необходимо изменить.
ДМ, лектор – Гонтовая Н.В.

40.

Операция
Если
стр.40
3
U – универсальное множество, то дополнением множества
А называется
множество всех тех элементов, которые являются
элементами множества
U, но не входят в множество А :
Варианты обозначения операции «дополнение множеств»:
Например:
Пусть
U–
множество всех возможных десятичных цифр
Тогда если множество
то дополнением множества
А
является множество
ДМ, лектор – Гонтовая Н.В.

41.

стр.41
U
ДМ, лектор – Гонтовая Н.В.

42.

стр.42
Дополнение множества
А возможно не только до
универсального множества, но и до любого другого
множества
Q , при условии, что
где верхний индекс
при символе
(т.е.
)
означает, что операция дополнения осуществляется
до множества
Например, если
то
ДМ, лектор – Гонтовая Н.В.

43.

стр.43
Свойства операции дополнения множеств:
1) Если
2) Если
3)
4)
5)
ДМ, лектор – Гонтовая Н.В.

44.

Операция
стр.44
4
(или относительным дополнением множеств)
А и В называется называется множество
всех элементов х , принадлежащих множеству А, но
не входящих в множество В :
Разностью множеств
Аналогично определяется разность множеств
ВиА:
ДМ, лектор – Гонтовая Н.В.

45.

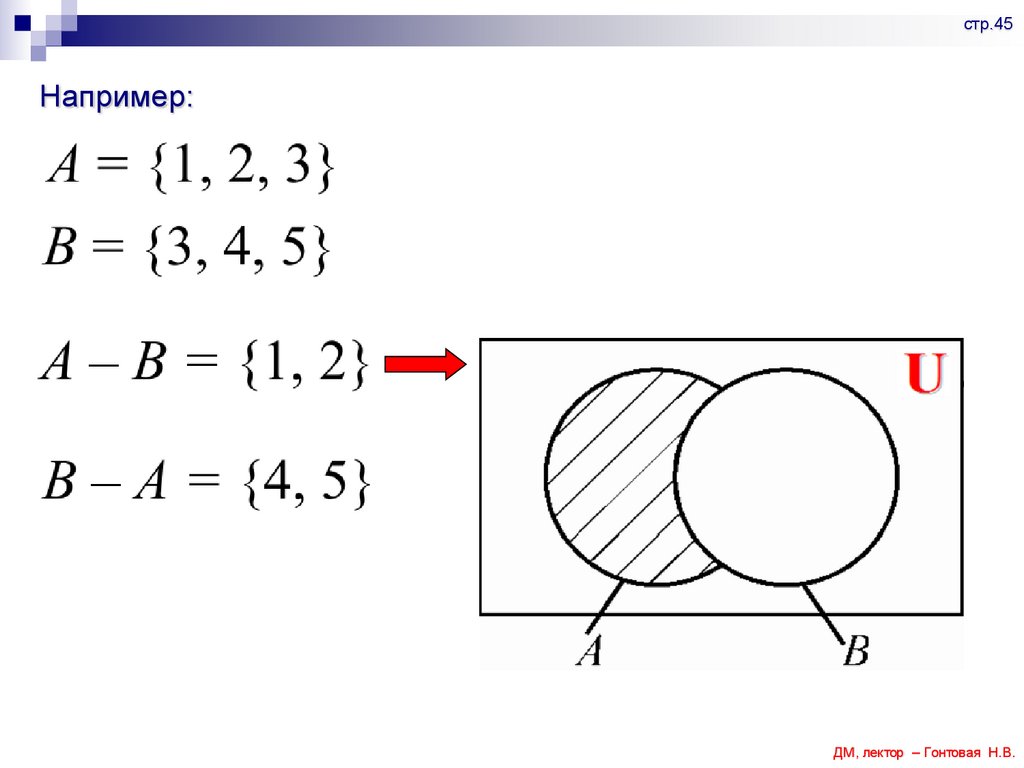
стр.45
Например:
ДМ, лектор – Гонтовая Н.В.

46.

стр.46
!!! Если
, то
!!!
То есть чтобы найти множество
, нужно
из множества А удалить все элементы,
принадлежащие множеству В.
В результате получится пустое множество.
ДМ, лектор – Гонтовая Н.В.

47.

стр.47
!!!
Если
То есть при
, то
разность
с дополнением множества
совпадает
А до множества В.
ДМ, лектор – Гонтовая Н.В.

48.

стр.48
!!! В тех случаях, когда разность множеств применяется к трём и
более множествам, необходимо использовать скобки, поскольку
то есть
разность множеств неассоциативна.
ДМ, лектор – Гонтовая Н.В.

49.

Операция
5
стр.49
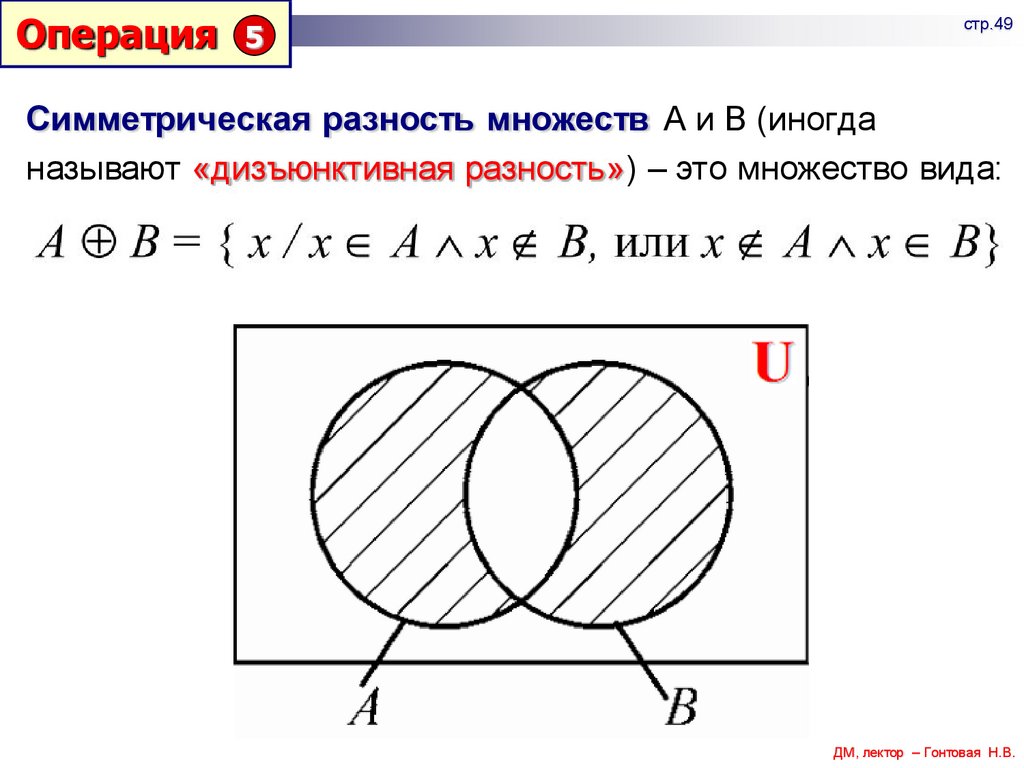
Симметрическая разность множеств А и В (иногда
называют «дизъюнктивная разность») – это множество вида:
ДМ, лектор – Гонтовая Н.В.

50.

стр.50
Симметрическая разность может быть выражена через
разность множеств и операцию объединения множеств:
Например, если
то
ДМ, лектор – Гонтовая Н.В.

51.

стр.51
Симметрическая разность может быть выражена через
операции дополнения, пересечения и объединения
множеств:
(1)
!!! В булевой алгебре операция
называется
«сложение по модулю 2» или «неравнозначность».
ДМ, лектор – Гонтовая Н.В.

52.

стр.52
Свойства симметрической разности:
1) свойство коммутативности
2) свойство ассоциативности
3) свойство дистрибутивности пересечения множеств
относительно симметрической разности
ДМ, лектор – Гонтовая Н.В.

53.

стр.53
Благодаря свойству дистрибутивности можно
раскрывать скобки в сложных выражениях.
Например:
ДМ, лектор – Гонтовая Н.В.

54.

стр.54
!!! Операция симметрической разности множеств
не является дистрибутивной относительно
пересечения этих множеств.
(2)
Для доказательства утверждения (2) следует выразить
обе части неравенства (2) через операции
объединения, пересечения и дополнения,
и результаты преобразования множеств представить
в виде диаграмм Венна.
ДМ, лектор – Гонтовая Н.В.

55.

стр.55
Преобразуем левую часть неравенства (2) в соответствии
с формулой (1):
ДМ, лектор – Гонтовая Н.В.

56.

стр.56
Аналогично преобразуем правую часть неравенства (2):
ДМ, лектор – Гонтовая Н.В.

57.

стр.57
Левая часть неравенства (2)
Правая часть неравенства (2)
На диаграммах Венна видно, что множества,
соответствующие левой и правой частям неравенства (2),
не совпадают, чтд.
ДМ, лектор – Гонтовая Н.В.

58.

стр.58
3
3.1 Законы де Моргана
Огастес (Августус) де Морган (1806 – 1871) – шотландский
математик-логик
Законы де Моргана устанавливают связь между операциями
объединения, пересечения и дополнения множеств.
ДМ, лектор – Гонтовая Н.В.

59.

стр.59
Закон 1: Дополнение объединения множеств есть
пересечение дополнений этих множеств:
Закон 2: Дополнение пересечения множеств есть
объединение дополнений этих множеств:
Д/З: Найти иллюстрации законов де Моргана на
диаграммах Венна
ДМ, лектор – Гонтовая Н.В.