1554190

1.

Множество, операции над
множествами. Диаграммы
Эйлера – Венна.

2.

Определение
Множество есть совокупность определенных вполне различаемых
объектов (субъектов), которые называются элементами, объединенных
некоторым свойством.
«Множество есть
многое, мыслимое нами как единое».
Основоположник
теории множеств немецкий математик
Георг Кантор
(1845-1918)

3.

Объекты, составляющие данное множество, называют его элементами.
Множество может быть конечным . Например, множество делителей числа
1 состоит из одного элемента – 1 – это множество является конечным.
Может быть бесконечным. Например, множество общих кратных чисел 2 и
3(6,12,18,24,…).
Может быть пустым. Например, множество чисел, делящихся на нуль.
Имеет специальное обозначение «
ø ».

4.

Множество обычно обозначают
большими латинскими буквами, а
элементы множества − малыми
латинскими буквами.
Элементы
множества
записываются в фигурных скобках:
А {а,в,с}.
Великий математик XVIII в.
Леонардо
Эйлер
предложил
изображать множества кругами, а
элементы множеств – точками
внутри этих кругов.

5.

В математике часто исследуются так называемые числовые множества,
т.е.
множества,
элементами
которых
являются
числа.
Для самых основных числовых множеств утвердились следующие
обозначения:

6.

Объединение множеств ( сложение )
Множество
элементов,
принадлежащих хотя бы одному из
множеств А и В , называют
объединением множеств А и В.
А В

7.

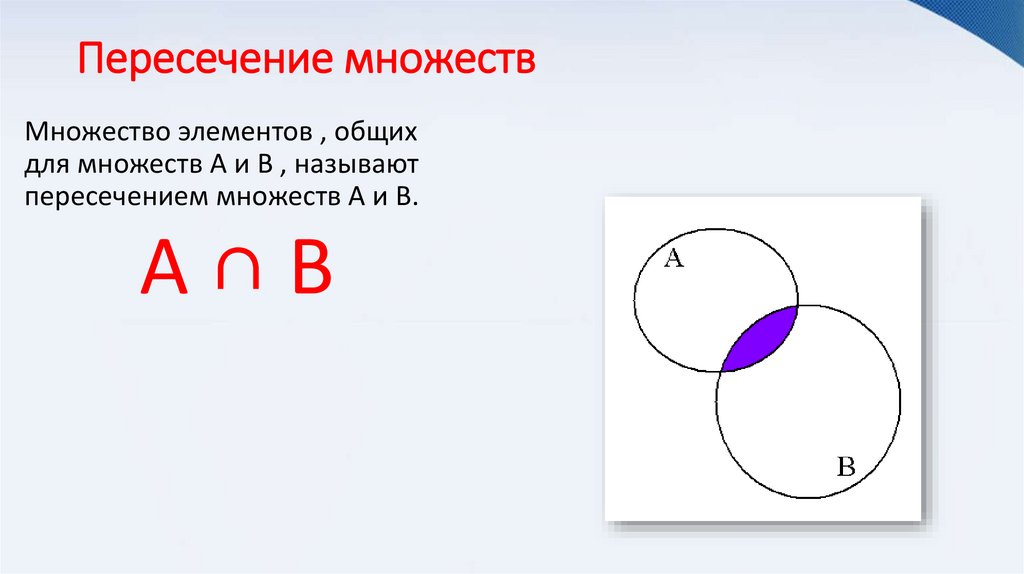
Пересечение множеств
Множество элементов , общих
для множеств А и В , называют
пересечением множеств А и В.
А∩В

8.

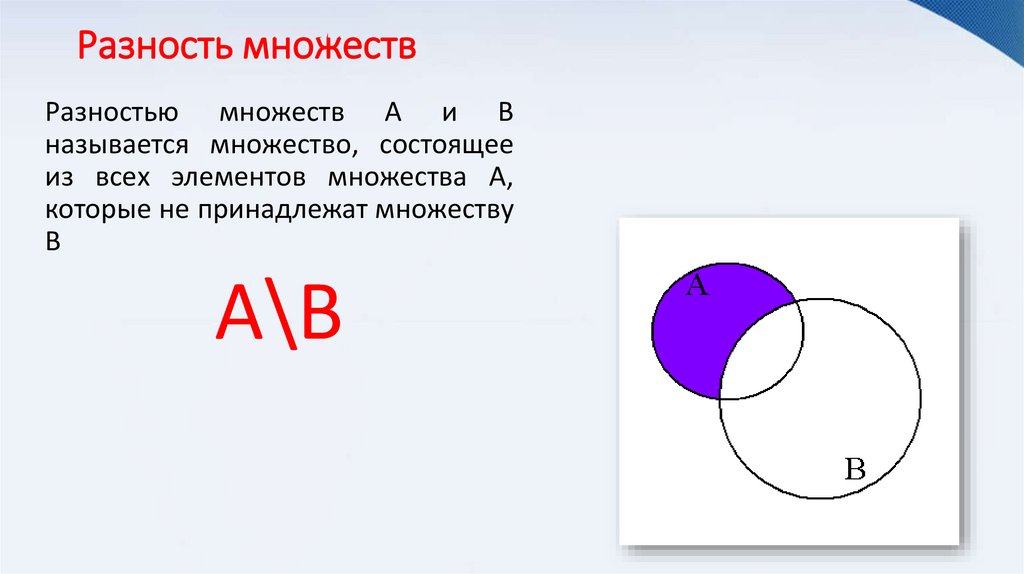
Разность множеств
Разностью множеств А и В
называется множество, состоящее
из всех элементов множества А,
которые не принадлежат множеству
В
А\В

9.

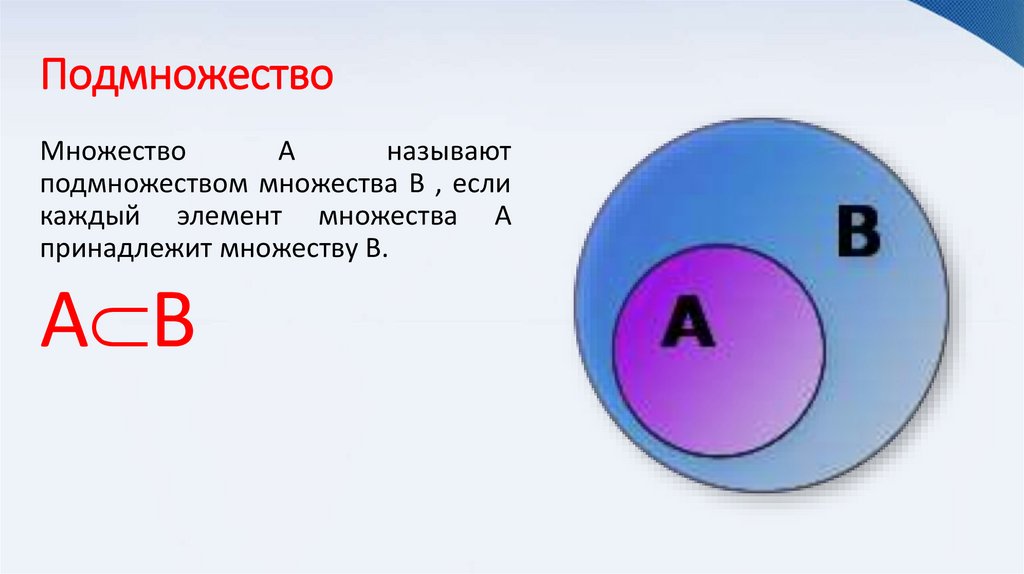
Подмножество
Множество
А
называют
подмножеством множества В , если
каждый элемент множества А
принадлежит множеству В.
А В

10.

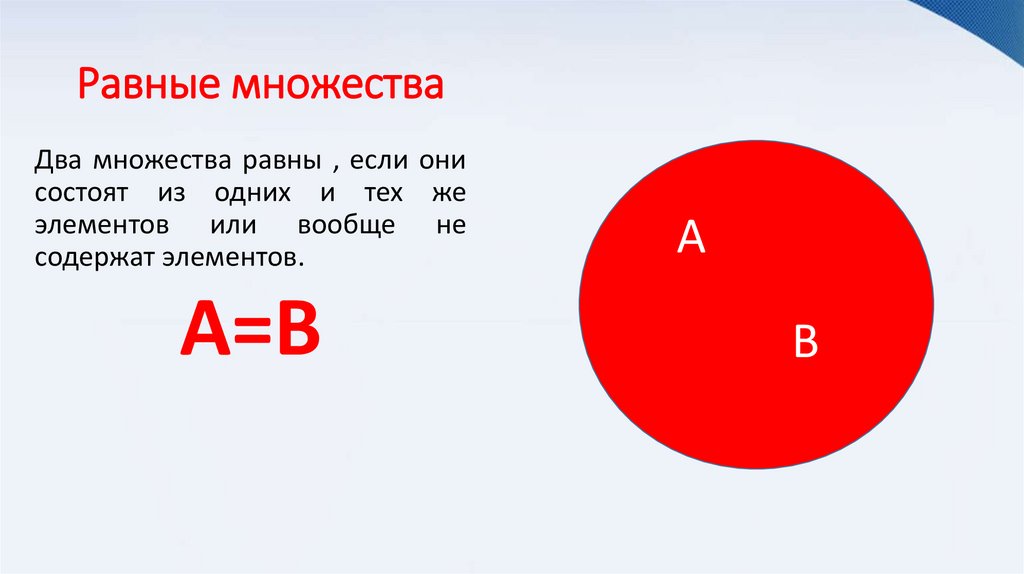
Равные множества
Два множества равны , если они
состоят из одних и тех же
элементов или вообще не
содержат элементов.
А=В
А
В

11.

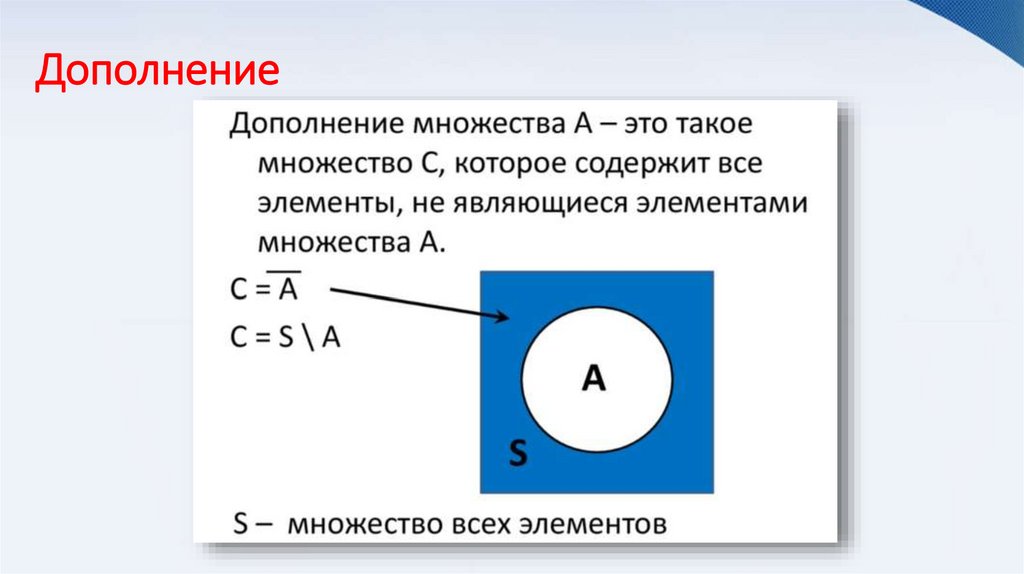
Дополнение

12.

Задание 1
Найдём все подмножества
множества {0, 1, 2}.
Решение
Это ∅, {0}, {1}, {2}, {0, 1}, {0, 2}, {1, 2},
{0, 1, 2}.

13.

Домашнее задание
1. Запишите все подмножества множества В = 3; 6: 9; 12}.