Similar presentations:
Множество, операции над множествами. Диаграммы Эйлера-Венна
1.
Множество, операции надмножествами. Диаграммы
Эйлера – Венна.
Подготовила:
Учитель математики
МБОУ Г.ГОРЛОВКИ «ШКОЛА № 42»
Рыбина М.В.
2.
ОпределениеМножество есть совокупность определенных вполне различаемых
объектов (субъектов), которые называются элементами, объединенных
некоторым свойством.
«Множество есть
многое, мыслимое нами как единое».
Основоположник
теории множеств немецкий математик
Георг Кантор
(1845-1918)
3.
Объекты, составляющие данное множество, называют его элементами.Множество может быть конечным . Например, множество делителей числа
1 состоит из одного элемента – 1 – это множество является конечным.
Может быть бесконечным. Например, множество общих кратных чисел 2 и
3(6,12,18,24,…).
Может быть пустым. Например, множество чисел, делящихся на нуль.
Имеет специальное обозначение «
ø ».
4.
Множество обычно обозначаютбольшими латинскими буквами, а
элементы множества − малыми
латинскими буквами.
Элементы
множества
записываются в фигурных скобках:
А {а,в,с}.
Великий математик XVIII в.
Леонардо
Эйлер
предложил
изображать множества кругами, а
элементы множеств – точками
внутри этих кругов.
5.
В математике часто исследуются так называемые числовые множества,т.е.
множества,
элементами
которых
являются
числа.
Для самых основных числовых множеств утвердились следующие
обозначения:
6.
Объединение множеств ( сложение )Множество
элементов,
принадлежащих хотя бы одному из
множеств А и В , называют
объединением множеств А и В.
А В
7.
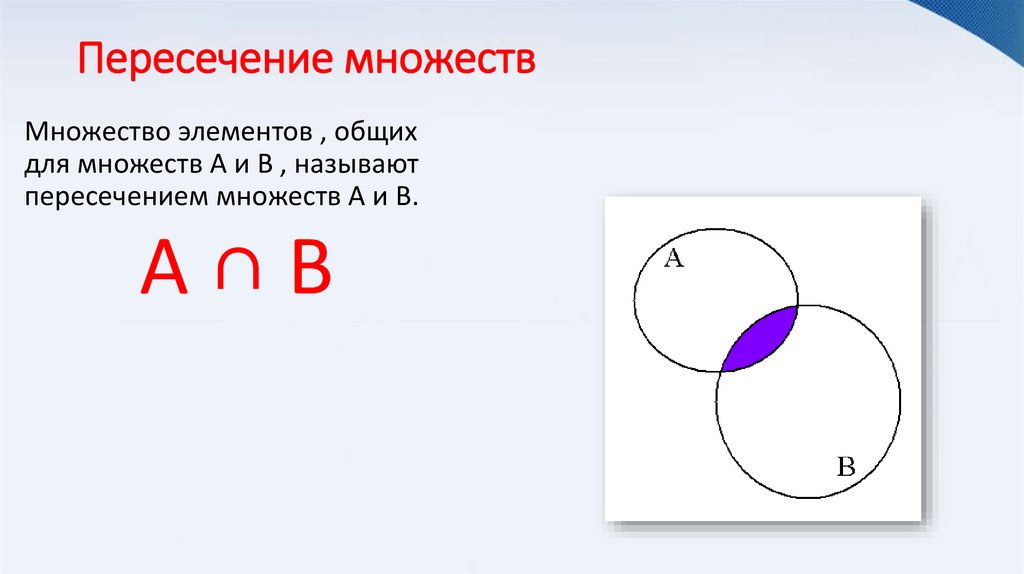
Пересечение множествМножество элементов , общих
для множеств А и В , называют
пересечением множеств А и В.
А∩В
8.
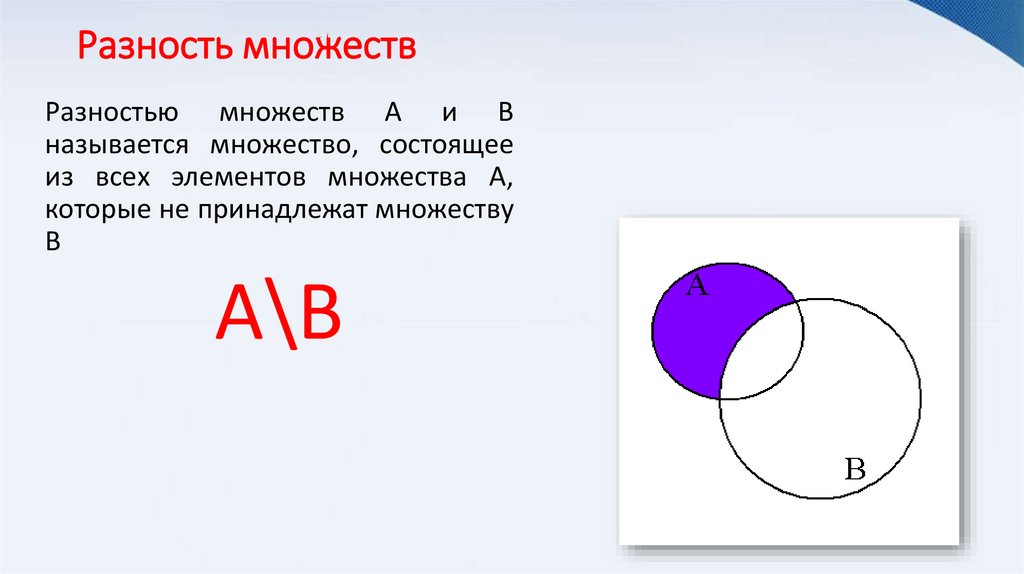
Разность множествРазностью множеств А и В
называется множество, состоящее
из всех элементов множества А,
которые не принадлежат множеству
В
А\В
9.
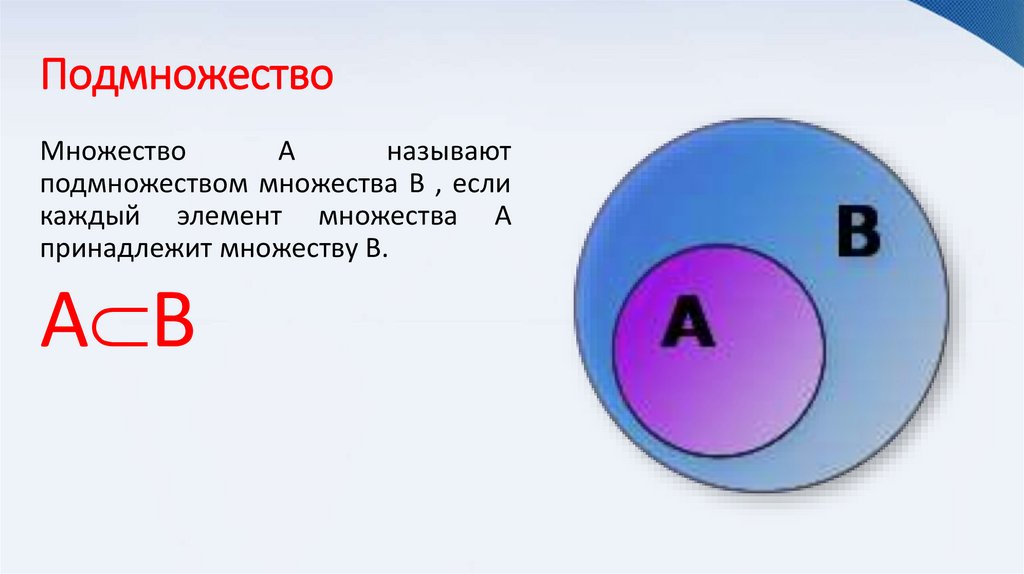
ПодмножествоМножество
А
называют
подмножеством множества В , если
каждый элемент множества А
принадлежит множеству В.
А В
10.
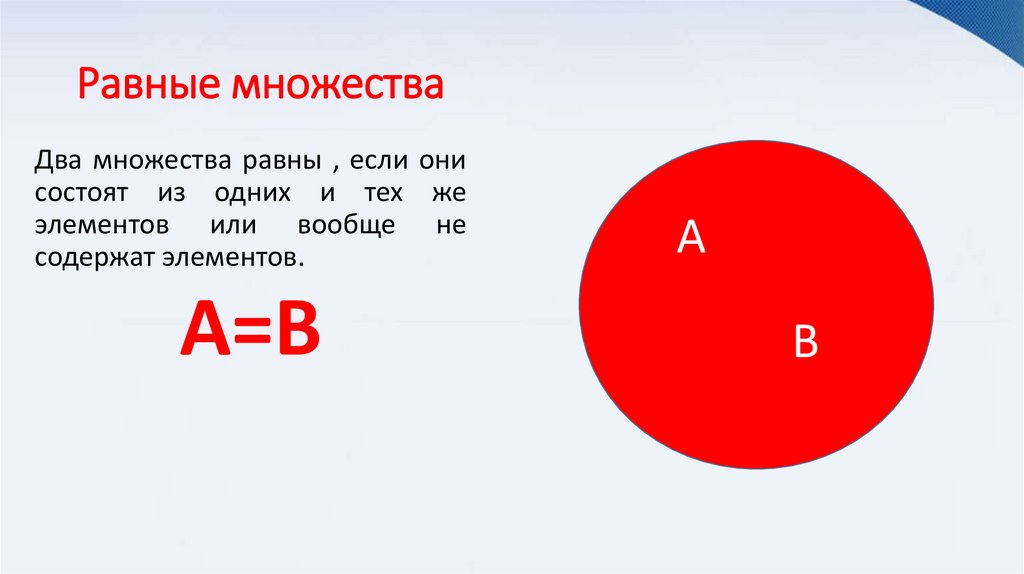
Равные множестваДва множества равны , если они
состоят из одних и тех же
элементов или вообще не
содержат элементов.
А=В
А
В
11.
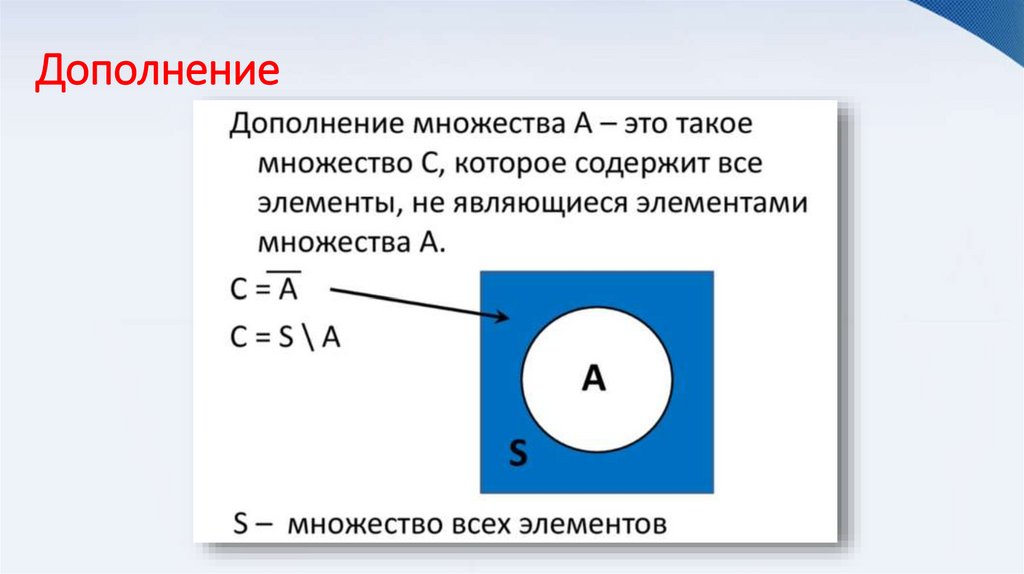
Дополнение12.
Задание 1Найдём все подмножества
множества {0, 1, 2}.
Решение
Это ∅, {0}, {1}, {2}, {0, 1}, {0, 2}, {1, 2},
{0, 1, 2}.
13.
Задание 2Пусть A = {1, 2, 3, 4, 5}, B = {1, 3, 5, 7, 9, 11}.
Найти A∪B, A ∩ B, A/B, B/А
Решение
A∪B = {1, 2, 3, 4, 5, 7, 9, 11}
A ∩ B = {1, 3, 5}
A/B = {2, 4}
B/А = {7, 9, 11}
14.
Задания 3 - 63. А = {простые числа, которые меньше 20 , В = {четные числа, которые
меньше 20}.
Найти А В, А В, А\В, В\А.
4. А = − 3; 5 , В = 2; 7 . Найдите А В, А В, А\В, В\А.
5. А = − 2; 4 , В = − ∞; 1 . Найдите А В, А В, А\В, В\А.
6. А = − 3; 4 , В = 1; +∞ . Найдите А В, А В, А\В, В\А.
15.
Домашнее задание1. Перечислите элементы множества В – множества простых чисел,
которые меньше 20.
2. Запишите все подмножества множества В = 3; 6: 9; 12}.
3. А = множество чисел кратных 3 и меньших 20},
В = { множество чисел кратных 2 и меньших 20}.
Найдите А В, А В, А\В, В\А.
4. А = − 4; 7 , В = 1; 9 . Найдите А В, А В, А\В, В\А.
5. А = − 3; 5 , В = − ∞; 2 . Найдите А В, А В, А\В, В\А.
6. А = − 2; 5 , В = 2; +∞ . Найдите А В, А В, А\В, В\А.










 mathematics
mathematics








