Similar presentations:
Множества. Отношения и операции над множествами. Диаграммы Эйлера-Венна
1.
МНОЖЕСТВАОТНОШЕНИЯ И ОПЕРАЦИИ
НАД МНОЖЕСТВАМИ
ДИАГРАММЫ ЭЙЛЕРА – ВЕННА
2.
Под множеством понимают, следуяоснователю теории Г. Кантору, «многое,
мыслимое как единое».
Множество
есть
совокупность
определенных вполне различаемых объектов
(субъектов),
которые
называются
элементами,
объединенных
некоторым
свойством.
3.
4.
5.
6.
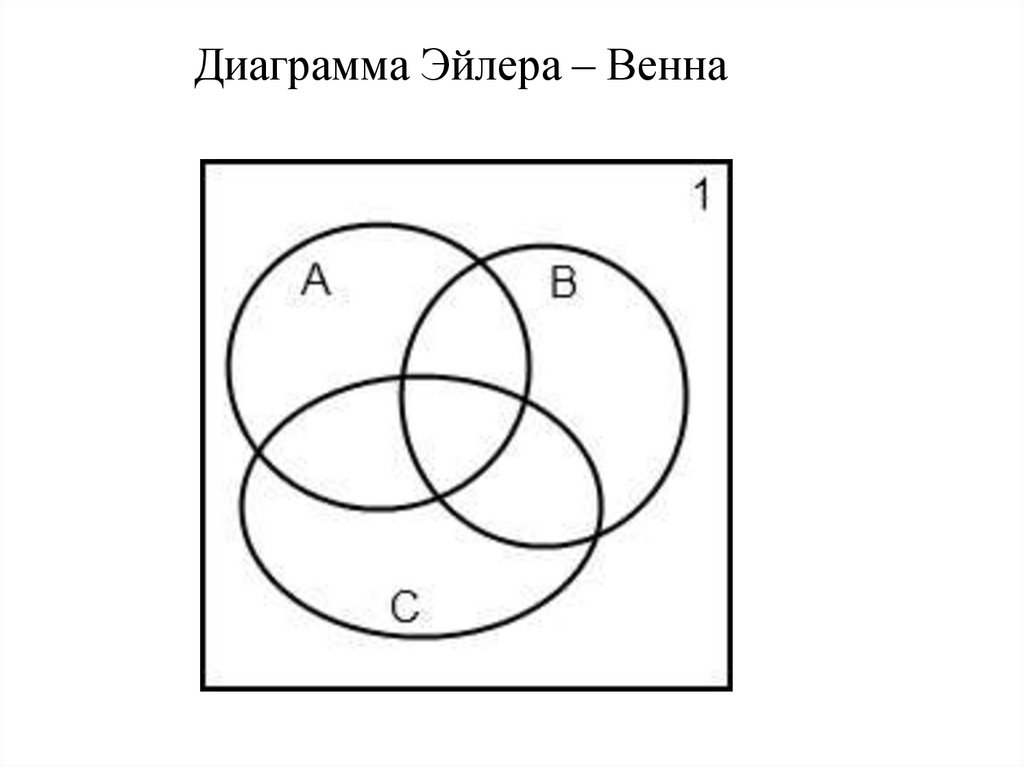
Диаграмма Эйлера – Венна7. Таблица отношений и операций над множествами
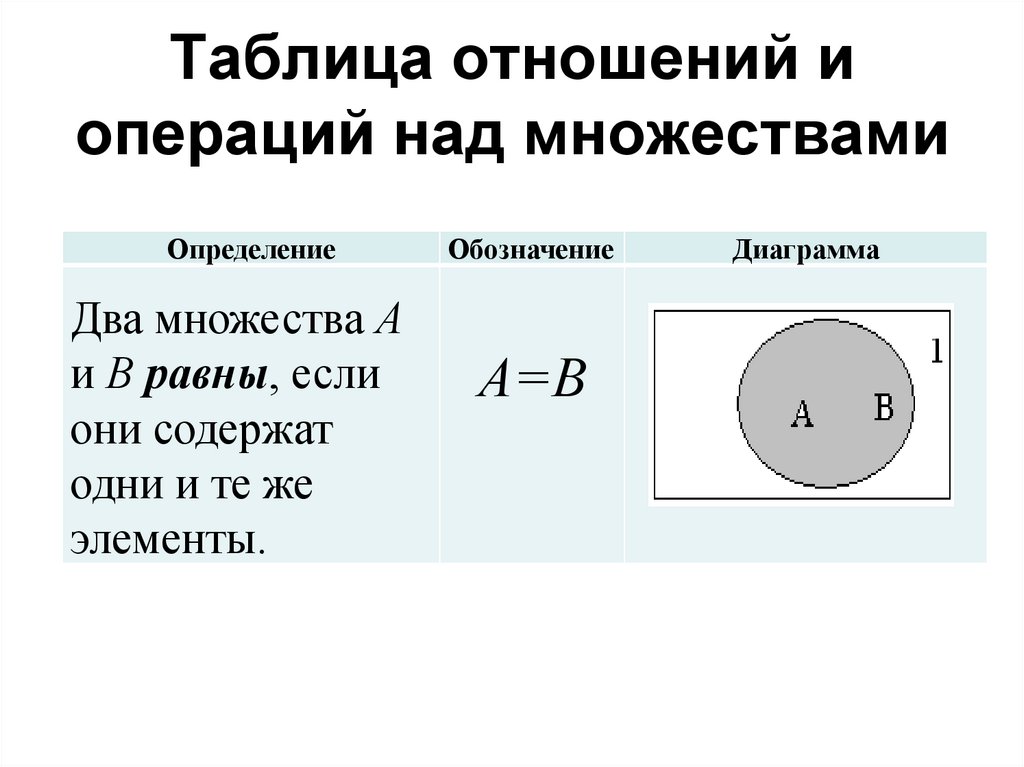
ОпределениеДва множества А
и В равны, если
они содержат
одни и те же
элементы.
Обозначение
А=В
Диаграмма
8.
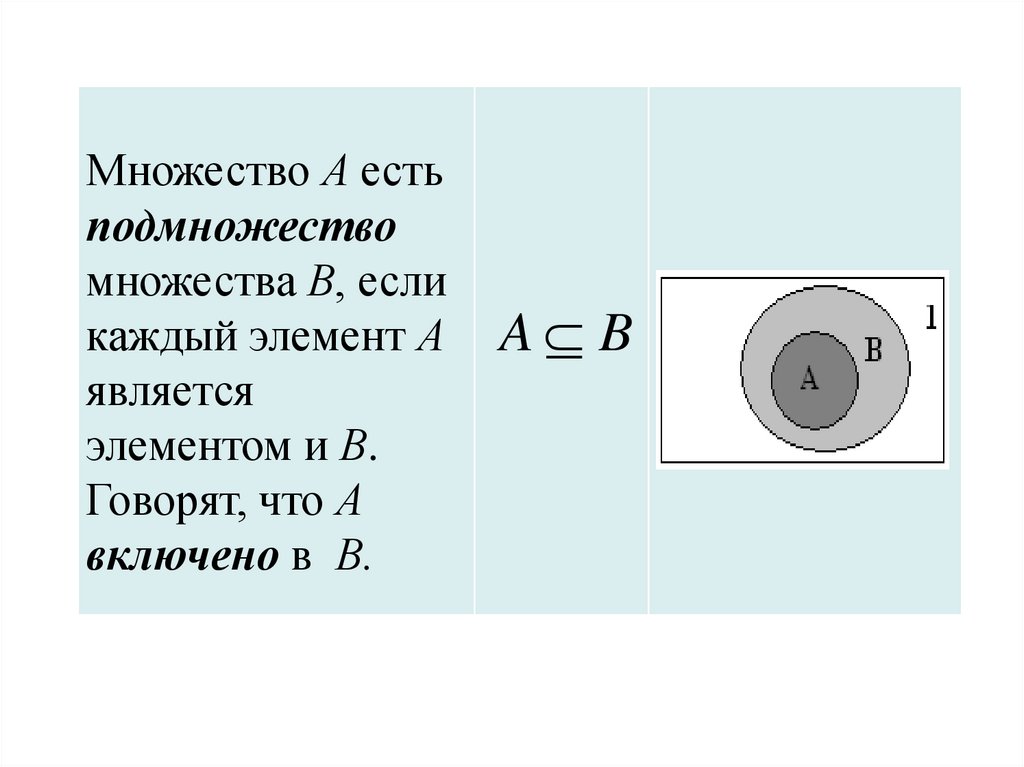
Множество А естьподмножество
множества В, если
каждый элемент А
является
элементом и В.
Говорят, что А
включено в В.
A B
9.
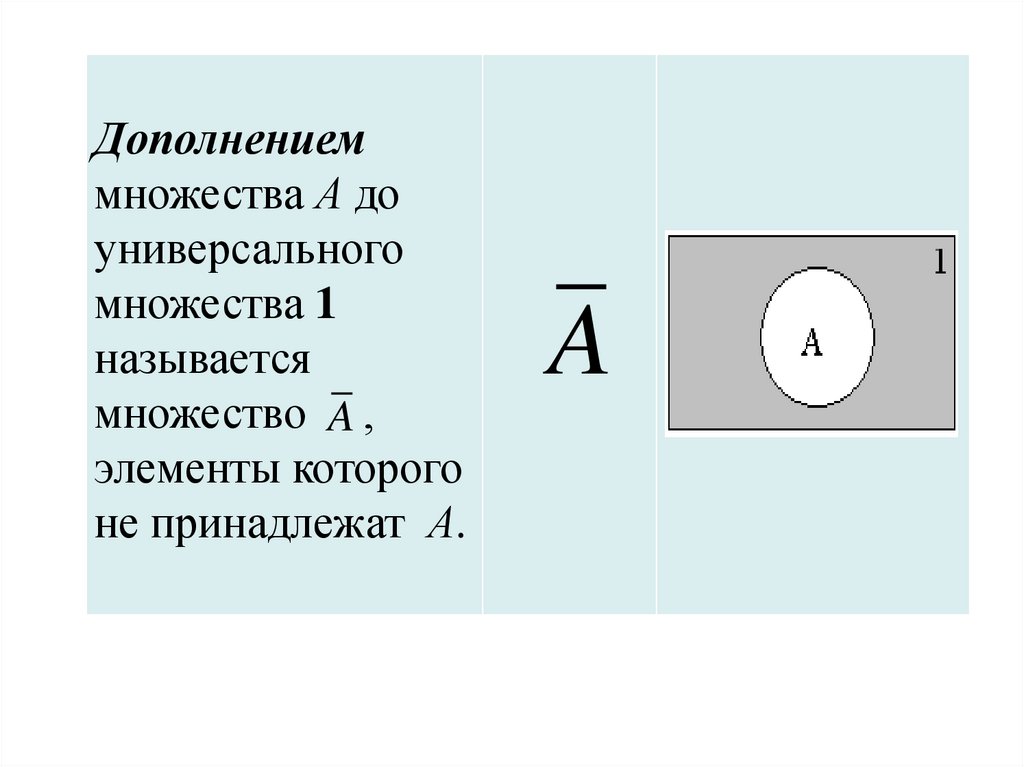
Дополнениеммножества А до
универсального
множества 1
называется
множество A ,
элементы которого
не принадлежат А.
A
10.
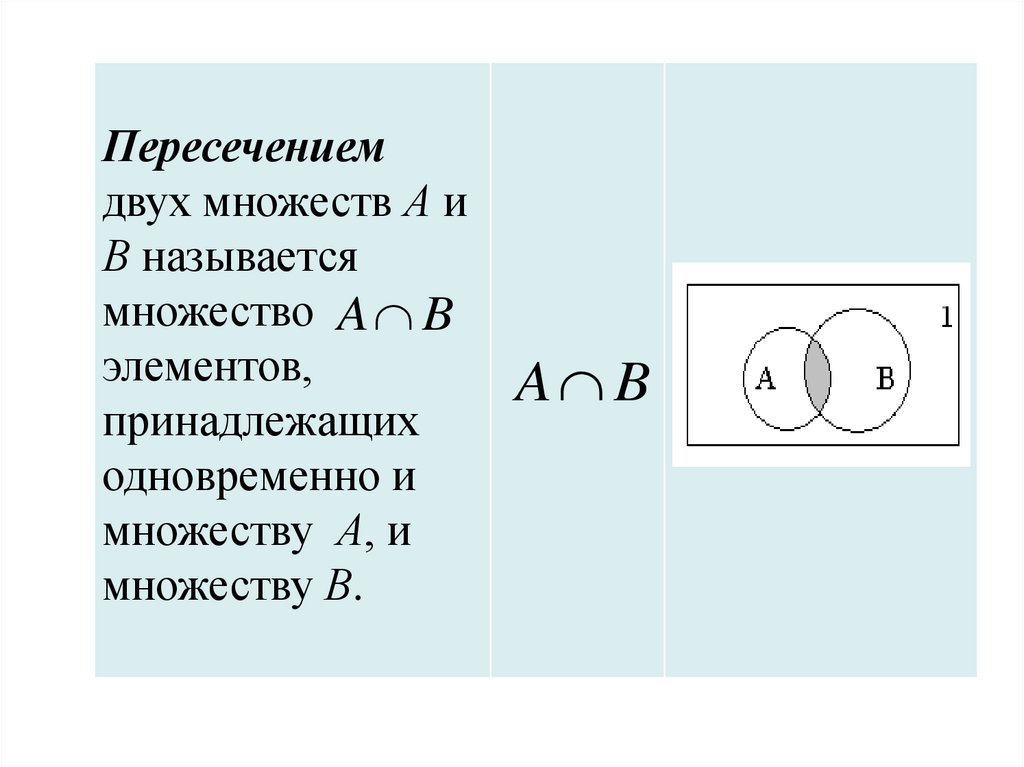
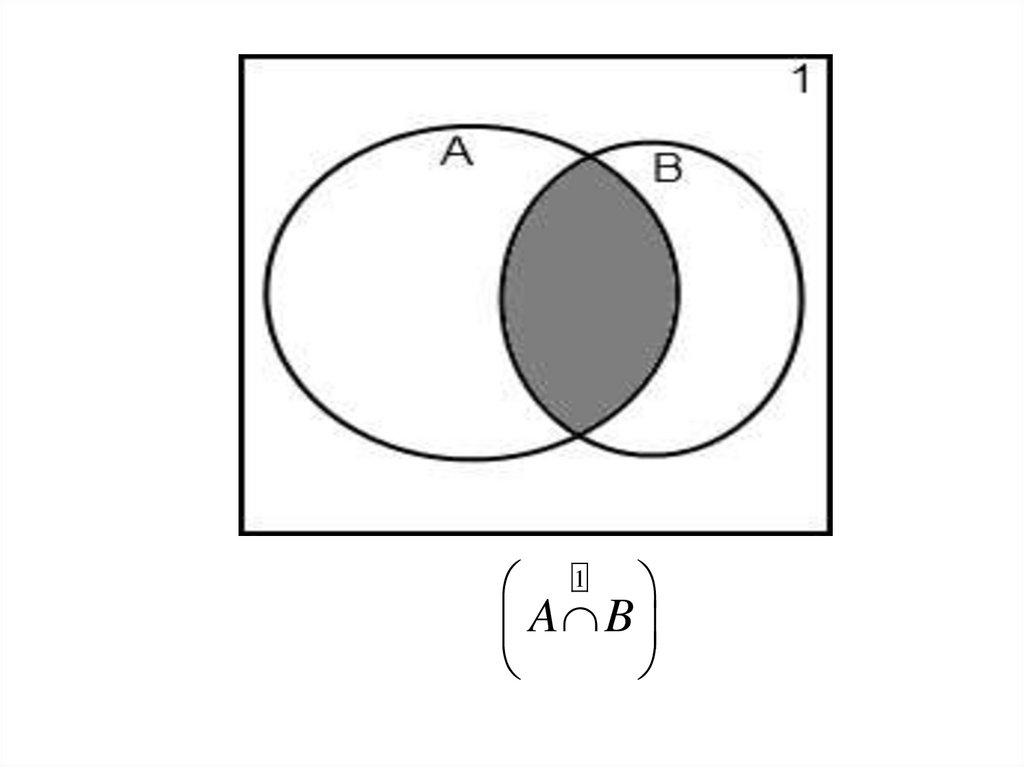
Пересечениемдвух множеств А и
В называется
множество A B
элементов,
принадлежащих
одновременно и
множеству А, и
множеству В.
A B
11.
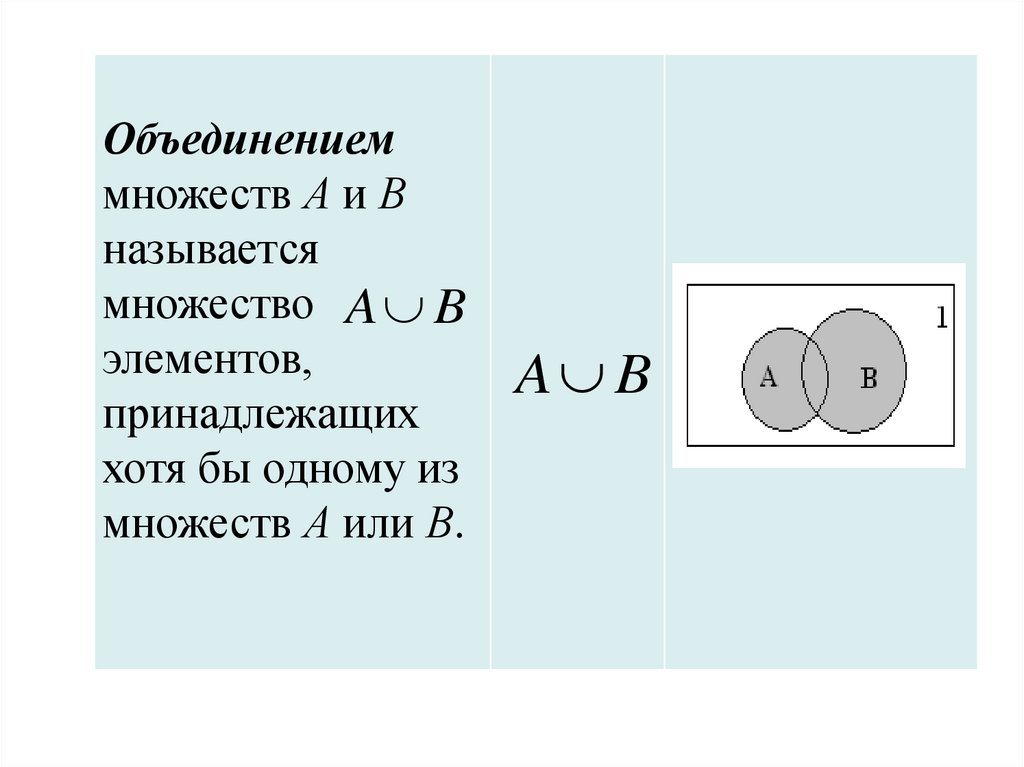
Объединениеммножеств А и В
называется
множество A B
элементов,
принадлежащих
хотя бы одному из
множеств А или В.
A B
12.
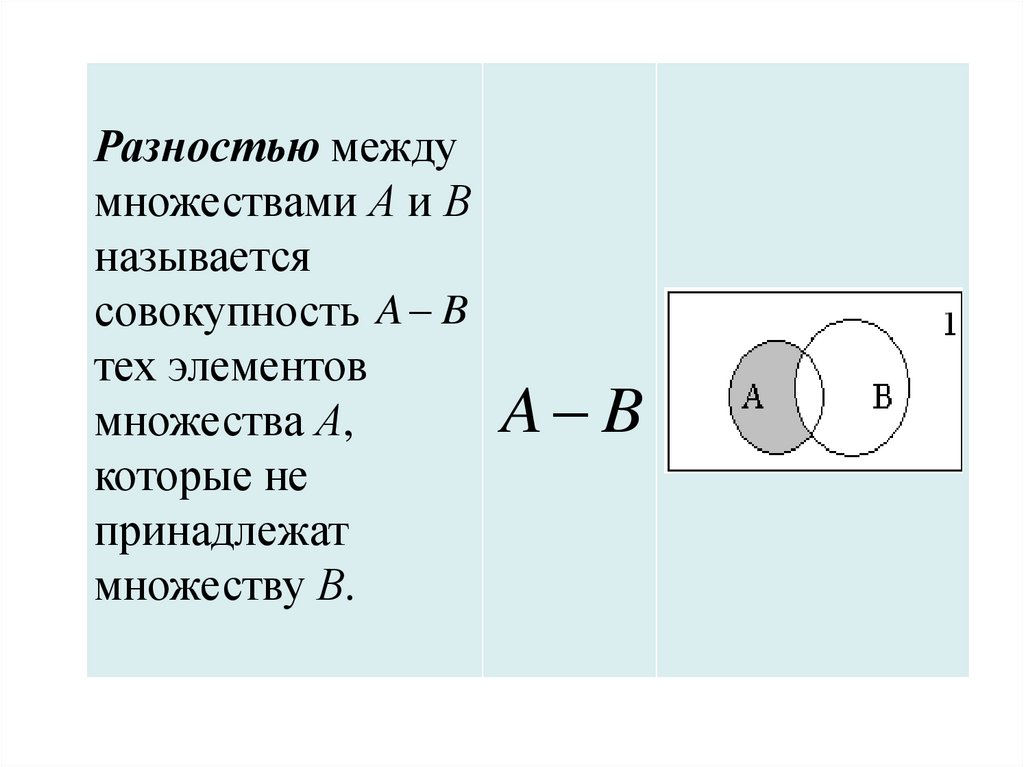
Разностью междумножествами А и В
называется
совокупность A B
тех элементов
A B
множества А,
которые не
принадлежат
множеству В.
13.
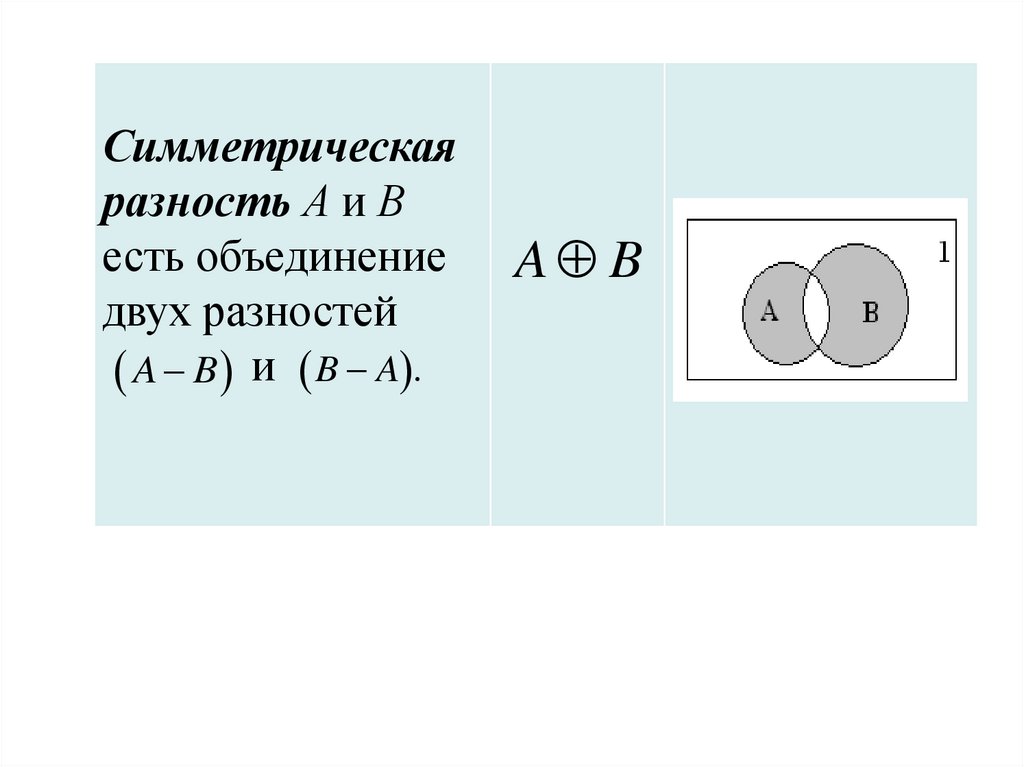
Симметрическаяразность А и В
есть объединение
двух разностей
A B и B A .
A B
14.
Пример, иллюстрирующий диаграммамиЭйлера – Венна справедливость следующего
отношения включения:
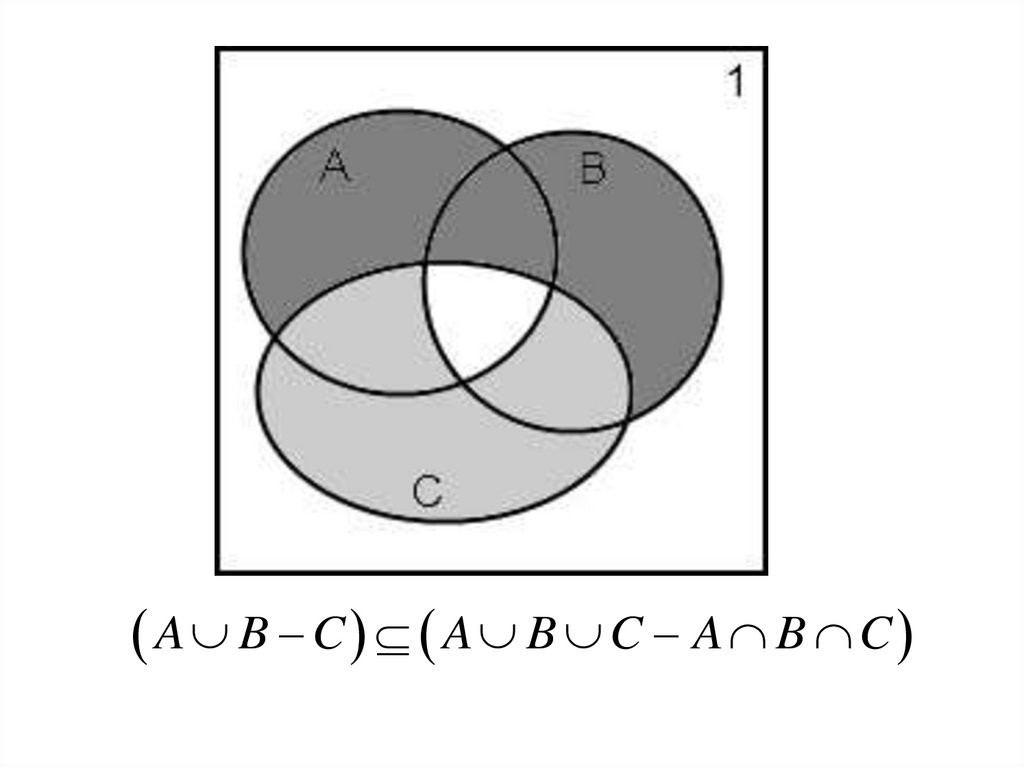
A B C A B C A B C
Порядок выполнения операций:
1 2 5 6 7 3 4
A B C A B C A B C
15.
Диаграмма Эйлера – Венна16.
1A B
17.
2A B C
18.
3A B
19.
4A B C
20.
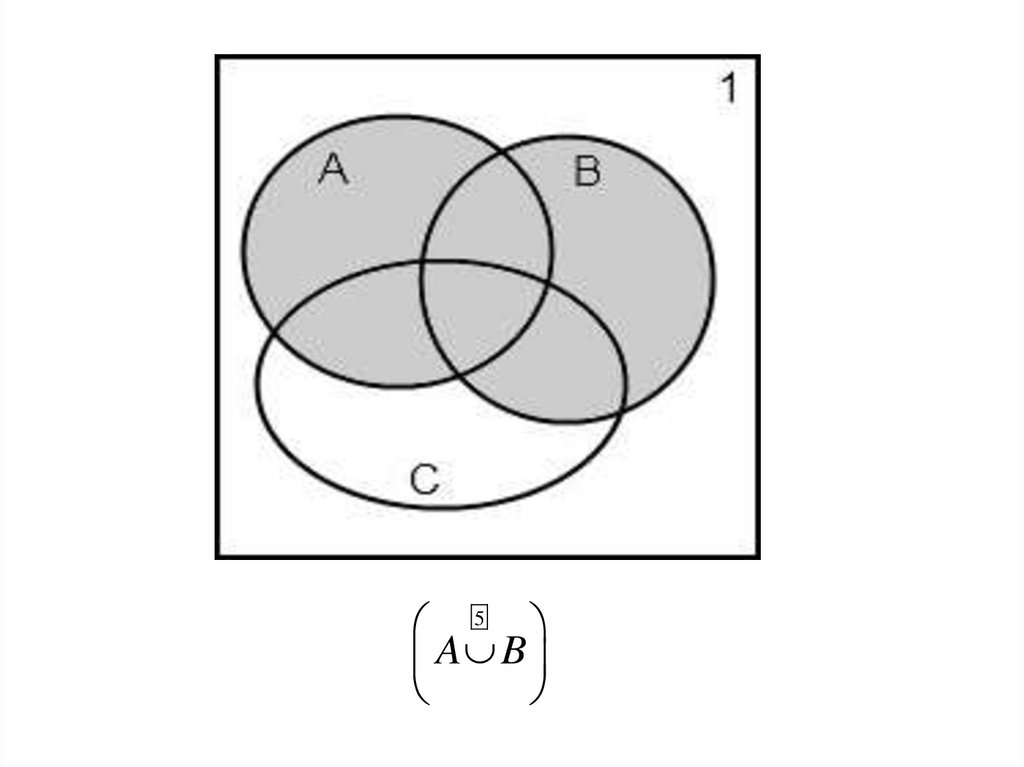
5A B
21.
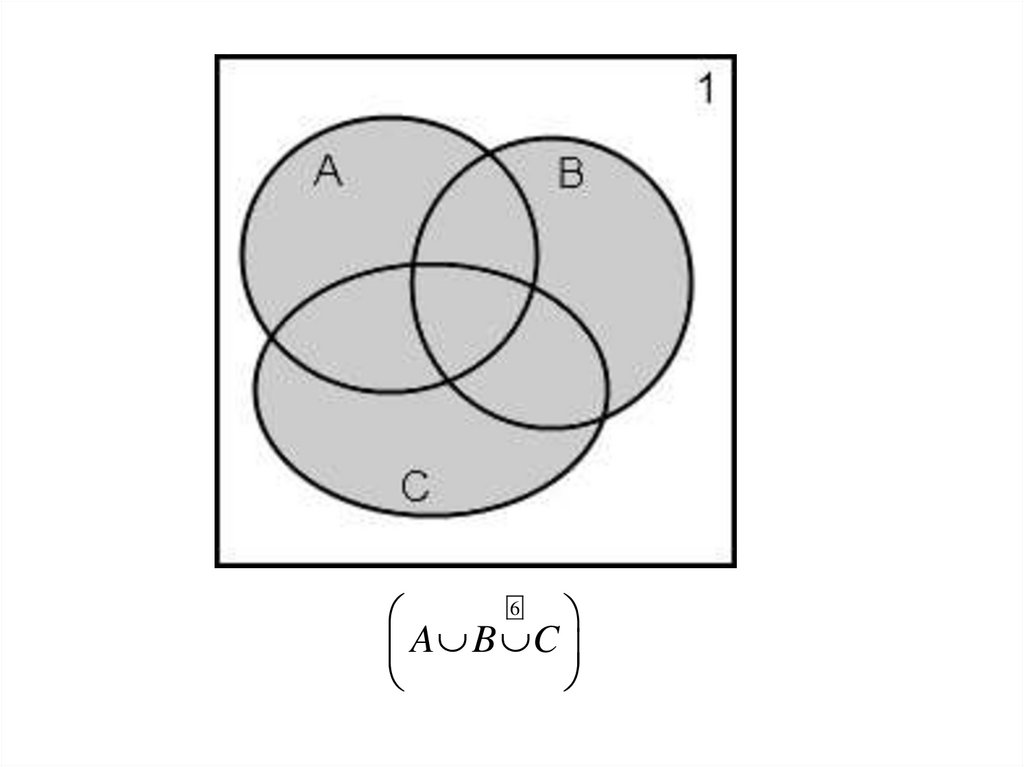
6A B C
22.
7A B C A B C
23.
A B C A B C A B C24.
Пример, иллюстрирующий диаграммамиЭйлера – Венна равенство множеств
A B A B A B
Порядок выполнения операций:
A B A B A B
3
2
1
4
25.
Диаграмма Эйлера – Венна26.
1A B
27.
B A B2
28.
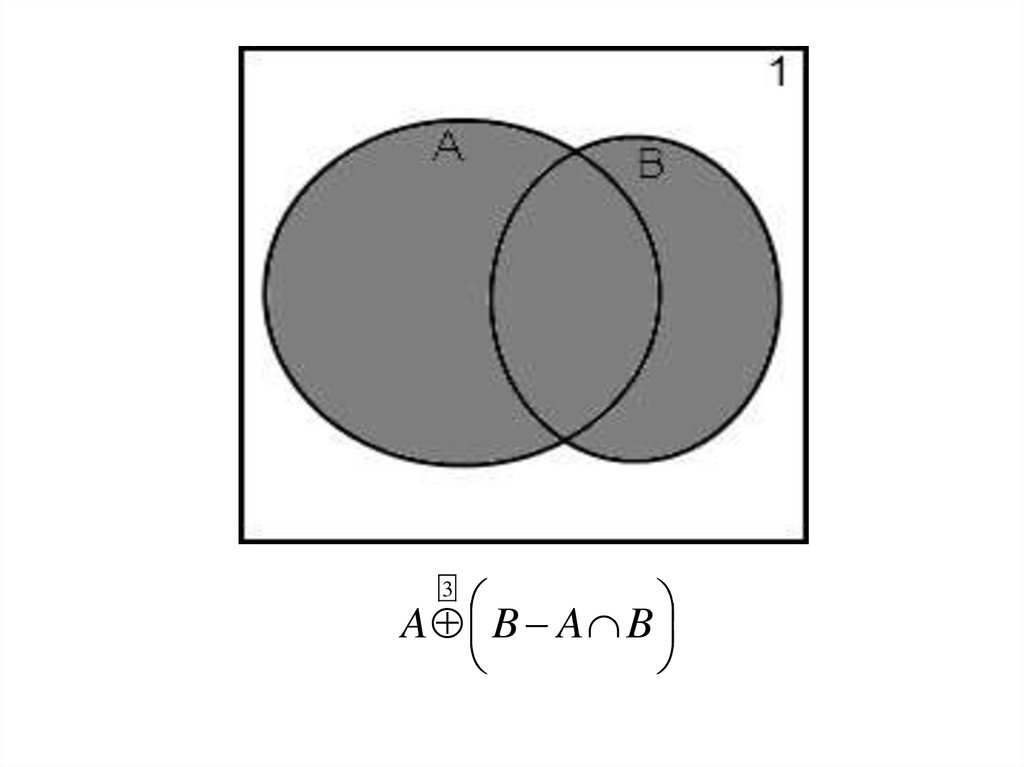
A B A B3
29.
4A B
















 mathematics
mathematics








