Similar presentations:
Множества. Отношения множеств. Операции над множествами
1. Множества. Отношения множеств. Операции над множествами.
12. Содержание
1.2.
3.
4.
Определение и обозначение множеств
Способы задания множеств
Отношения между множествами
Операции над множествами
2
3. Определение и обозначение множеств
Множество – основное понятие теориимножеств, возникшей в конце XIX века, её
основатель – немецкий ученый Георг
Кантор.
Множество – группа объектов,
объединенных общими признаками.
Множества обозначают заглавными
латинскими буквами, элементы множеств
заключают в фигурные скобки через
запятую.
A = {1,3,5,7,9}
B = {1,3,4 }
3
4.
Множества могут быть конечными и бесконечными.Конечные множества состоят из конечного числа
элементов.
Например: А={1,3,5,7,9} -однозначное, натуральное,
нечетное.
Бесконечные множества имеют бесконечное число
элементов.
Примеры бесконечных множеств:
{N} – множество натуральных чисел
{Z} – множество целых чисел
{Q} – множество рациональных чисел
{R} – множество действительных чисел
Пустое множество – множество, не содержащее ни
одного элемента.
Обозначение: {Ø}
4
5. Способы задания множеств
а) Перечислениевсех элементов
через запятую
б) Указание
характеристического
свойства
Данный способ
позволяет задавать
как конечные, так и
бесконечные
множества.
5
6.
Характеристическоесвойство – свойство,
которым обладает каждый элемент
данного множества и не обладает ни один
элемент, ему не принадлежащий.
Пример 1.
Указать характеристическое свойство множества
А = {12,22,32,42,52,62,72,82,92};
Решение: Все перечисленные элементы являются
натуральными, двузначными и оканчиваются
цифрой 2.
6
7. Отношения множеств
Элементы одного множества могут бытьодновременно элементами и других
множеств, то есть быть подмножествами
множеств.
Множество В является подмножеством
множества А, если каждый элемент
множества В является одновременно
элементом множества А.
Обозначение: В⊂А, если А = {2,4,6,8};
В = {4,6,8}
7
8. Подмножества множеств
Множество, состоящее из n-элементовимеет 2n подмножеств.
Пустое множество является подмножеством
любого множества.
Каждое множество считается
подмножеством самого себя.
8
9. Пример 2. Найти все подмножества множества А
Пусть А = {1;2;3;4}, состоит из 4-ёхэлементов, значит n=4. Тогда множество
А имеет 24 =16 подмножеств:
{1 }; { 2 }; { 3 }; { 4 }, {1;2}, {1; 3}, {1; 4}, {2;3}, {2;4},
{3;4}, {1;2;3}, {1;2;4}, {2;3;4}, {1;3;4}, {1;2;3;4}, {Ø}.
9
10.
Равные множестваМножества А и В называют равными ,если
они состоят из одних и тех же элементов,
причем порядок их расстановки не имеет
значения.
Обозначение: А = В, если А = {2,4,6,8};
В = {4,8,2,6}.
Множество, состоящее из n элементов, имеет
n! равных множеств.
10
11. Операции над множествами
1.2.
3.
4.
5.
Пересечение множеств
Объединение множеств
Разность множеств
Дополнение множеств
Декартово произведение
11
12. Пересечение множеств
— пересечением множествА и В называется множество, содержащее все
элементы, которые принадлежат и множеству А и
множеству В.
Пересечение: А ∩ В
Пусть А = {1;2;3;4}, В = {3;4;5;6;7}, тогда А∩В = {3;4}
12
13. Объединение множеств
— объединениеммножеств А и В называется множество,
содержащее все элементы обоих множеств,
причем одинаковые элементы дважды не
перечисляются.
Объединение: А ∪ В
Пусть A = {1,2,3,4},B = {3,4,5,6,7}, тогда
А∪В = {1,2,3,4,5,6,7}
13
14. Разность множеств
Разностью множеств А и В называется множество,содержащее все элементы множества А, не
принадлежащие множеству В.
Разность: А\В
Пусть А = {1,2,3,4}, В = {3,4,5,6,7}, тогда
А\В = {1,2}
14
15. Дополнение множества
Дополнением множества А до множества Вназывается множество, содержащее все элементы
множества В, которые не принадлежат множеству
А.
В\А
Дополнение множества А до В обозначается В\А
Пусть А = {1,2,3,4}, В = {3,4,5,6,7}, тогда дополнением
множества А до В
В\А = {5,6,7}
15
16. Декартово произведение
Декартовым произведением множеств А и Вназывается множество всех пар, образованных из
элементов обоих множеств, первая компонента
которых принадлежит множеству А, а вторая
компонента принадлежит множеству В.
Декартово произведение множеств А и В
обозначают А×В. Используя это обозначение,
декартово произведение можно записать так:
А ×В= {(х;y)|х ∈ А , у ∈ В}
16
17.
Задача 1. Найдите декартово произведениемножеств А и В, если:
а) А={m;p}, B={e,f,k};
б) А=В= {3,5}
Решение: а) Действуем согласно
определению – образуем все пары, первая
компонента которых выбирается из А, а
вторая – из В.
А × В={(m;e),(m;f),(m;k),(p;e),(p;f),(p;k)}
б) Декартово произведение равных
множеств находят, образуя все возможные
пары из элементов данного множества:
А × А= {(3;3),(3;5),(5;3),(5;5)}
17
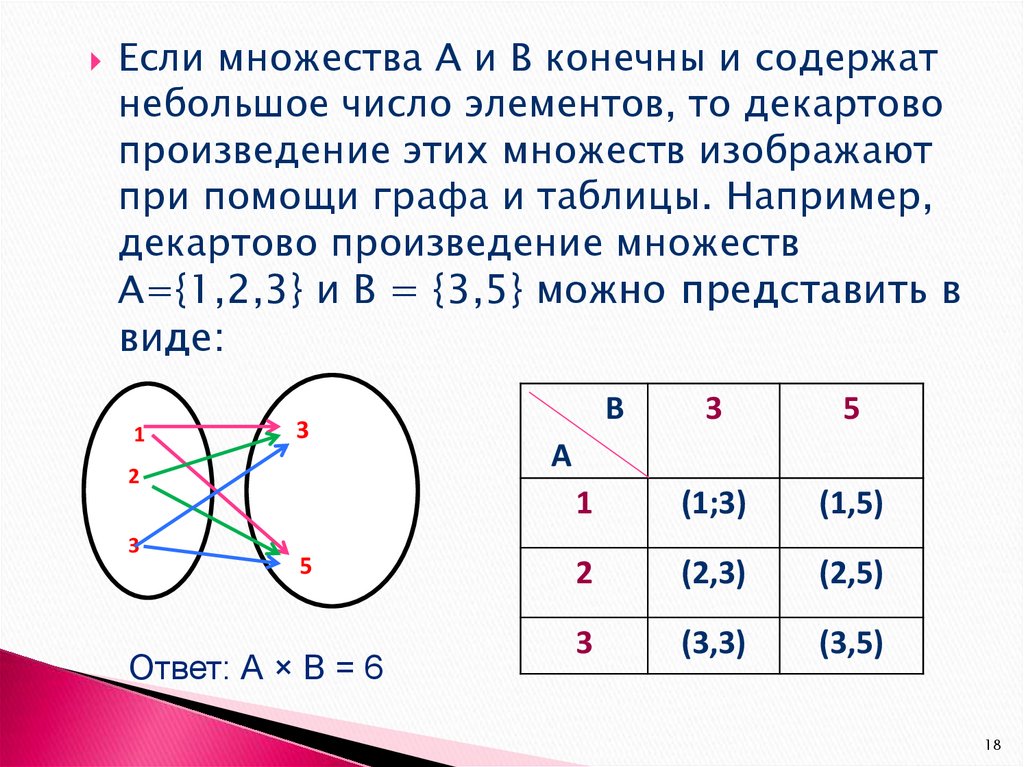
18.
Если множества А и В конечны и содержатнебольшое число элементов, то декартово
произведение этих множеств изображают
при помощи графа и таблицы. Например,
декартово произведение множеств
А={1,2,3} и В = {3,5} можно представить в
виде:
1
3
2
3
5
Ответ: А × В = 6
В
3
5
1
(1;3)
(1,5)
2
(2,3)
(2,5)
3
(3,3)
(3,5)
А
18

















 mathematics
mathematics








