2025_Лекция_1_Основные_понятия_теории_множеств_и_бинарных_отношений

1. Основные понятия теории множеств и бинарных отношений

Компьютерная дискретная математика
Основные понятия теории
множеств и бинарных
отношений

2.

2

3. Множество. Элементы множества

Множество – это некоторая совокупность
элементов, объектов, понятий.
Элементы множества – это объекты, которые
образуют данное множество, могут обладать
некоторыми свойствами и находиться в некоторых
отношениях между собой или с элементами других
множеств.
Порядок элементов в множестве не имеет значения
3

4. Обозначения

Множества обозначают заглавными, а
элементы множеств – строчными латинскими
буквами или строчными латинскими буквами с
индексами.
Запись А={a,b,d,h} означает, что множество
А состоит из четырех элементов a, b, d, h.
Утверждение, что конечное множество A
состоит из n элементов, записывается так:
A={a1,a2,...,an}.
4

5.

5

6.

6

7. Обозначения

Принадлежность
элемента
множеству
обозначается символом : a A (читают: элемент
а принадлежит множеству А).
В противном случае обозначают a A
(читают: элемент а не принадлежит множеству А).
Элементами множеств могут быть другие
множества, тогда эти элементы могут обозначаться
заглавными буквами.
7

8. Обозначения

Пример.
A = {D,C},
D={a, b},
C={c, d, e}.
При этом D A, C A, но a A и с A.
Пример.
A = {{x,y},z}.
Эта запись означает, что множество A содержит
два элемента: множество {x,y} и элемент z.
8

9. Конечные и бесконечные множества

Множество называется конечным, если оно
содержит
конечное
число
элементов
и
бесконечным, если оно содержит неограниченное
число элементов.
Пример.
Множество A={1,2,3,4,5,6,7,8,9,0}
цифр в
десятичной системе счисления конечно.
Множество точек окружности бесконечно.
9

10. Упорядоченные множества

Упорядоченным считается такое множество, в
котором важен порядок следования элементов.
Например,
упорядоченным
является
множество, в котором каждый элемент имеет свой
порядковый номер.
Обозначают упорядоченное множество, как
правило, либо
круглыми, либо треугольными
скобками.
A=<1,2,3>, в общем случае: A=<a1,a2,..,an>, n N;
В=(а,b,с).
10

11.

11

12. Способы задания множеств

Перечисление элементов
А = {a1, a2,... , an}.
Пример.
Например, множество студентов обозначим Zс и
зададим его перечислением:
Zс = {Иванов, Петров, Сидоров, Кукушкина}
12

13. Равенство множеств

Пример.
Пусть A - множество остатков, получаемых
при последовательном делении натуральных
чисел {3, 4, 5, 6,…} на 3:
A={0, 1, 2, 0, 1, 2, 0, 1, 2, 0, …}.
Это множество содержит всего три элемента:
0, 1, 2.
Поэтому его можно записать в виде
A={0, 1, 2}.
13

14.

14

15.

15

16.

16

17. Способы задания множеств

Задание с помощью характеристического
свойства
Множество Х = {х | Р(x)}, где Р(х) означает,
что элемент х обладает свойством P(x).
Пример.
Множество N10 всех натуральных чисел,
меньших 10 можно задать так:
N10={x | x N, x<10}.
17

18.

18

19. Подмножество

Множество А, все элементы которого принадлежат
множеству
В, называется подмножеством
множества В.
Обозначение: A B; A B.
Пример.
A – множество действительных чисел;
B – множество натуральных чисел.
Множество В является подмножеством множества А.
19

20.

20

21.

21

22. Равенство множеств

Неупорядоченные множества равны, если
они содержат одинаковый набор элементов.
Обозначается A=B.
Если множества не равны, это обозначается
A B.
22

23. Равенство множеств. Двухстороннее включение

А=В тогда и только тогда, когда из условия
x A следует x B и из условия y B следует y A.
Пример.
Пусть заданы множества
A = {1,2,3,4,5};
B – множество натуральных чисел от 1 до 5;
С = {c | 1 c 5, c N};
D = {4,1,5,2,3}.
Эти множества содержат один набор
элементов, поэтому
A=B=C=D
23

24. Строгое и нестрогое включение

Нестрогое включение обозначается А В,
означает, что А – подмножество множества В,
возможно совпадающее с В.
Строгое включение обозначается А В, и
означает, что А – подмножество множества В, не
совпадающее с B.
А В читается “А включено в В”.
24

25. Строгое и нестрогое включение. Равенство множеств

Выполнение соотношений А В и В А
возможно только при А = В. А = В, если А В и
B А.
Эти соотношения являются признаком
равенства
множеств
через
отношение
включения.
Иногда в литературе символом обозначают
"нестрогое"
включение,
допускающее
и
равенство множеств. В этом случае символ не
используется, а строгое включение записывают
двумя соотношениями A B, A B.
25

26. Строгое и нестрогое включение

Пример.
X – множество студентов группы КН-05-7,
Y – множество отличников в группе КН-05-7.
Тогда Y X,
Z – множество студентов потока КН-05-7,8,9,10.
Тогда X Z.
Включение X в Z строгое, поскольку кроме
учеников класса Х, в школе обязательно
присутствуют ученики других классов.
26

27. Универсальное множество

Универсальным называется
содержащее
все
возможные
встречающиеся в данной задаче.
Универсальное
символом U.
множество
множество,
элементы,
обозначается
Универсальное
множество
U
может
отличаться для каждой отдельной задачи и
определяется условием задачи.
27

28. Пустое множество

Пустым называется такое множество,
которое не содержит никаких элементов.
Пустое множество обозначается специальным
символом .
Пустое
множество
является
подмножеством любого множества, т.е. А,
где А – любое множество.
28

29. Пустое множество

Пустое множество – это множество,
поэтому, если некоторое множество A не
содержит ни одного элемента, то A= ; |A|=0.
Запись A={ } означает, что A содержит один
элемент – , |A|=1.
29

30. Множество-степень (булеан)

Множество всех подмножеств множества X
назовем множеством-степенью X или булеаном и
обозначим P (X).
Для произвольного множества X из n элементов
его множество-степень P (X) содержит 2n элементов:
P (X) = 2X =2 X = 2n
Пример.
A={a, b, c}.
2A={ ,{a},{b},{c},{a,b},{b,c},{a,c},{a,b,c}}
Пустое
множество
имеет
только
одно
подмножество – само пустое множество, поэтому
P( )={ }.
30

31.

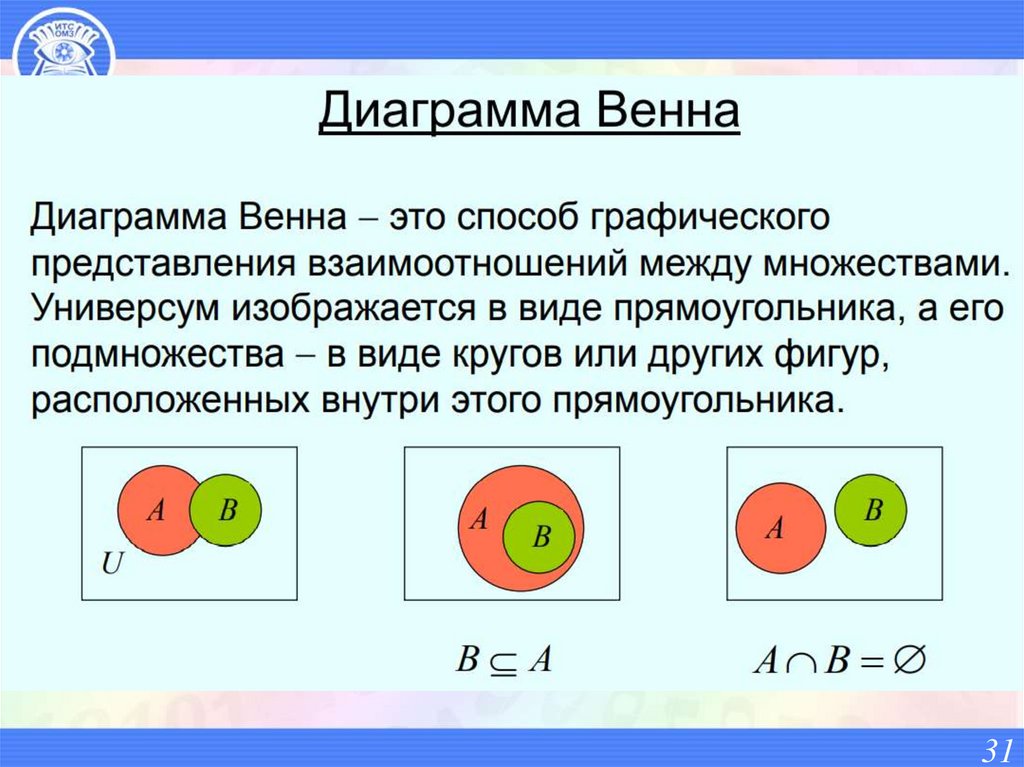
31

32. Геометрическая интерпретация множеств : диаграммы Венна

Построение диаграммы Венна заключается в
разбиении плоскости на 2n ячеек с помощью n
замкнутых фигур (где n – число изображаемых
множеств). Каждая фигура на диаграмме
представляет отдельное из 2n подмножеств
множество.
32

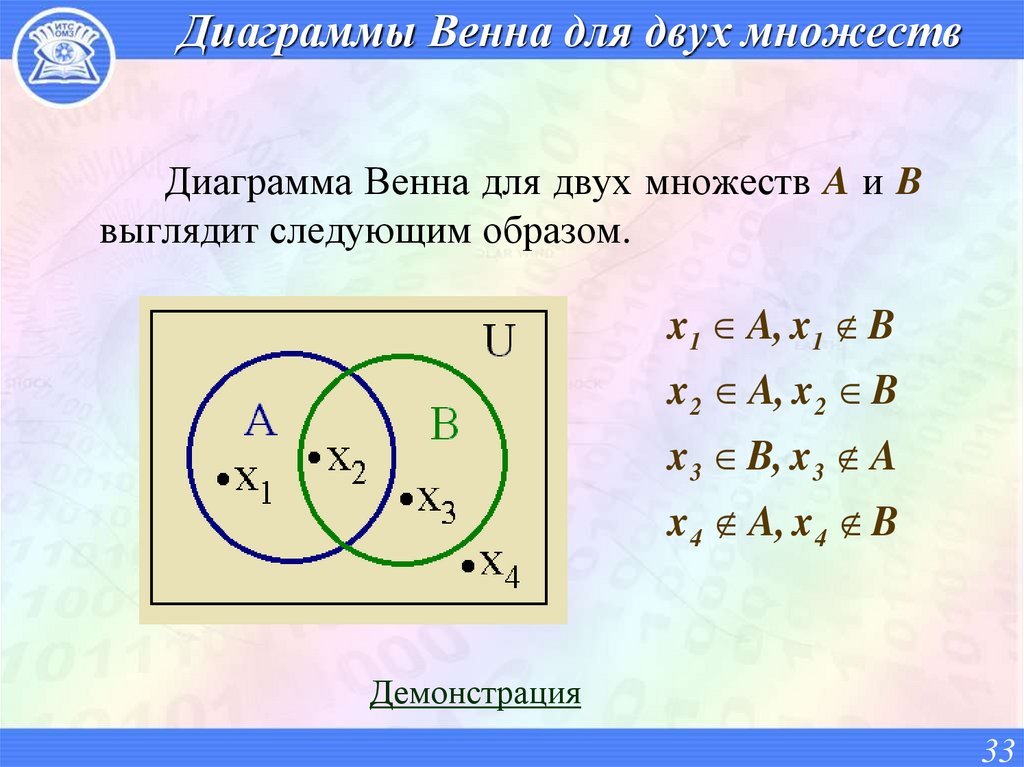
33. Диаграммы Венна для двух множеств

Диаграмма Венна для двух множеств A и B
выглядит следующим образом.
x1 A, x1 B
x 2 A, x 2 B
x 3 B, x 3 A
x 4 A, x 4 B
Демонстрация
33

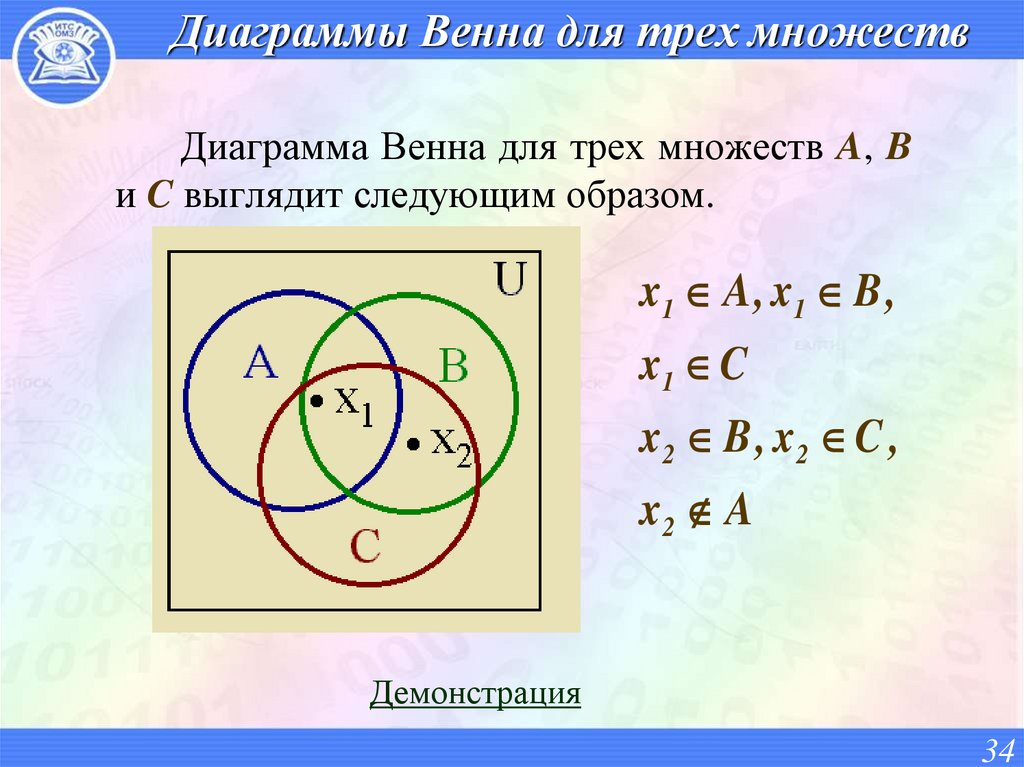
34. Диаграммы Венна для трех множеств

Диаграмма Венна для трех множеств A, B
и C выглядит следующим образом.
x1 A , x1 B ,
x1 C
x2 B , x2 C ,
x2 A
Демонстрация
34

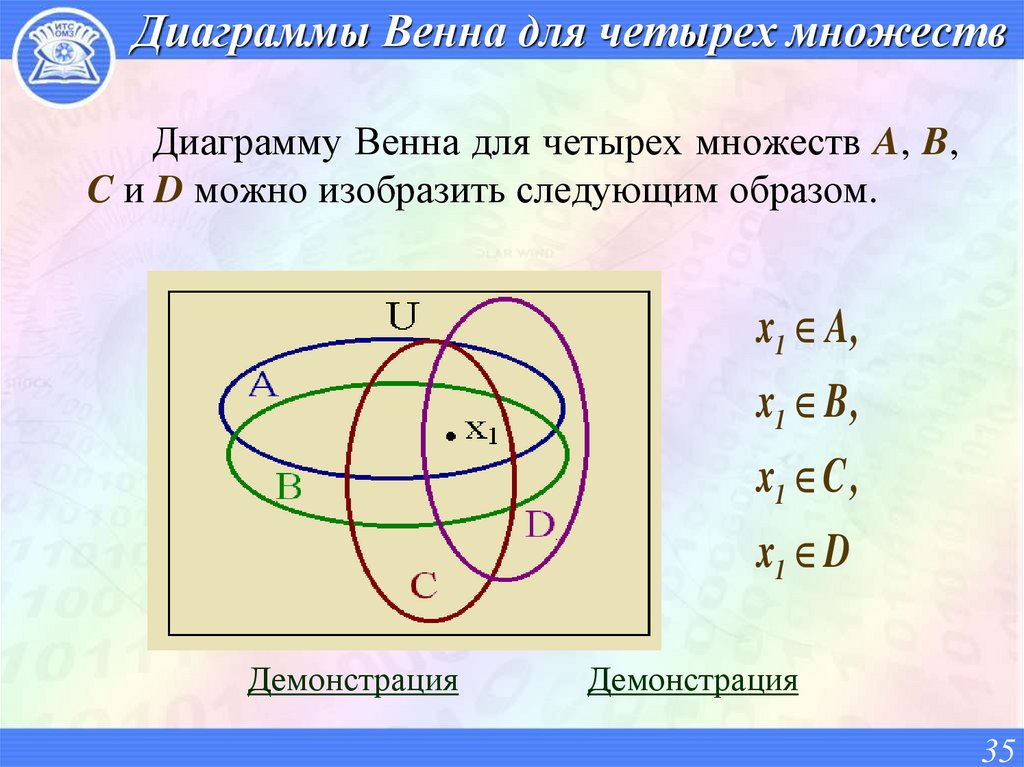
35. Диаграммы Венна для четырех множеств

Диаграмму Венна для четырех множеств A, B,
C и D можно изобразить следующим образом.
x1 A ,
x1 B ,
x1 C ,
x1 D
Демонстрация
Демонстрация
35

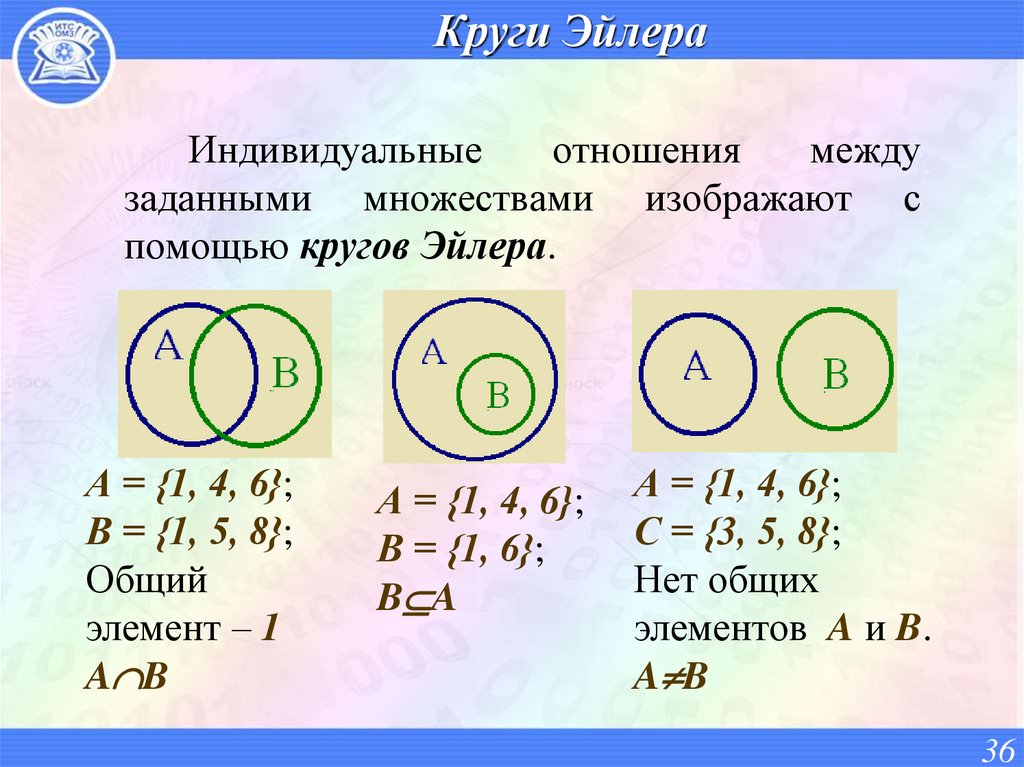
36. Круги Эйлера

Индивидуальные
отношения
между
заданными множествами изображают с
помощью кругов Эйлера.
А = {1, 4, 6};
В = {1, 5, 8};
Общий
элемент – 1
A B
А = {1, 4, 6};
В = {1, 6};
B A
А = {1, 4, 6};
С = {3, 5, 8};
Нет общих
элементов A и B.
A B
36

37. Алгебра множеств

Множество
2U
всех
подмножеств
универсального множества U, с заданными на нем
четырьмя операциями, составляют алгебру
множеств.
37

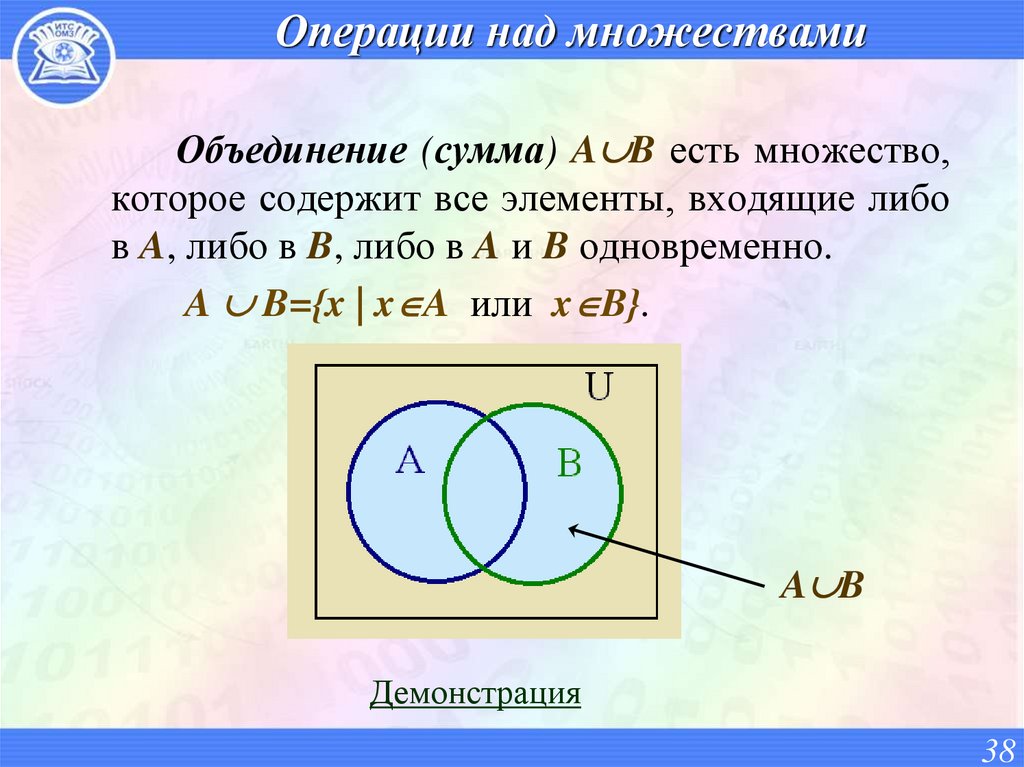
38. Операции над множествами

Объединение (сумма) A B есть множество,
которое содержит все элементы, входящие либо
в A, либо в B, либо в A и B одновременно.
A B={x | x A или x B}.
A B
Демонстрация
38

39.

39

40. Операции над множествами

Пример .
Пусть даны множества:
А={a, b, m};
В={m, n, c, p}.
А В= {a, b, c, m, n, p}
40

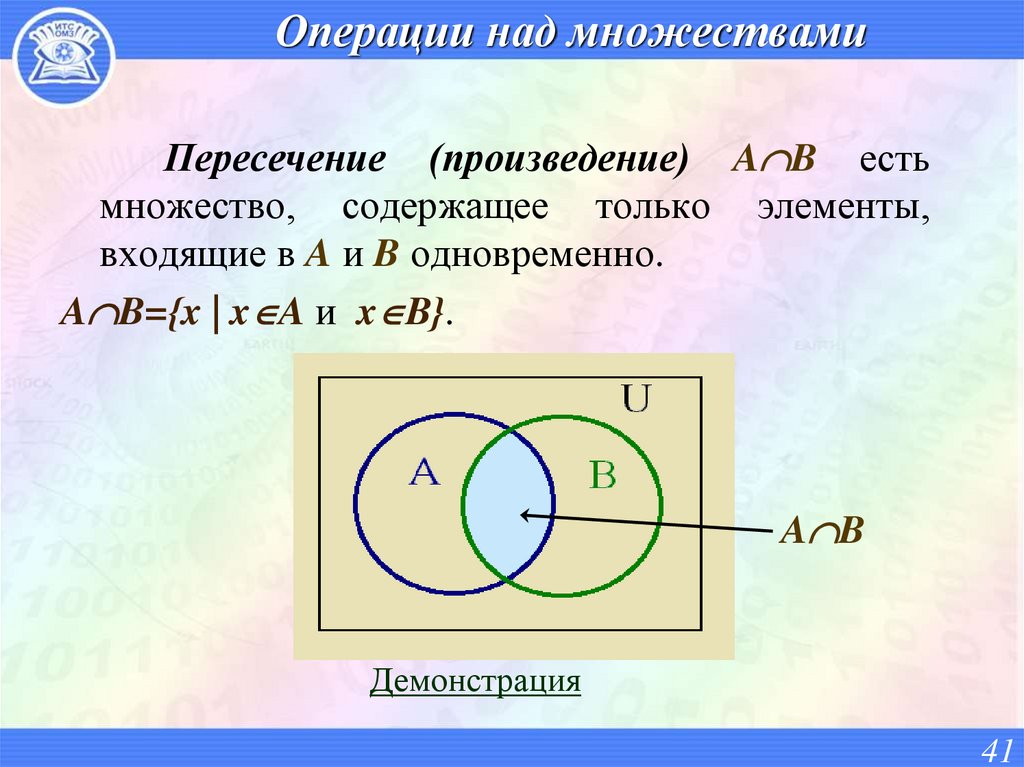
41. Операции над множествами

Пересечение (произведение) A B есть
множество, содержащее только элементы,
входящие в A и B одновременно.
A B={x | x A и x B}.
A B
Демонстрация
41

42.

42

43. Операции над множествами

Пример .
Пусть даны множества:
А={a, b, m};
В={m, n, c, p}.
А В = {m}
43

44. Операции над множествами

Дополнение (отрицание) Ā (читается “не
А”) есть множество U\A.
A = {x | x A}.
Демонстрация
44

45. Операции над множествами

Пример .
Z = {…,-2,-1,0,1,2,…}.
В этой задаче U=Z.
Пусть Z- – множество отрицательных
чисел и 0, тогда
Z- = {… -2, -1, 0}.
Дополнением к множеству Z- будет
множество натуральных чисел
N={1,2,…}.
45

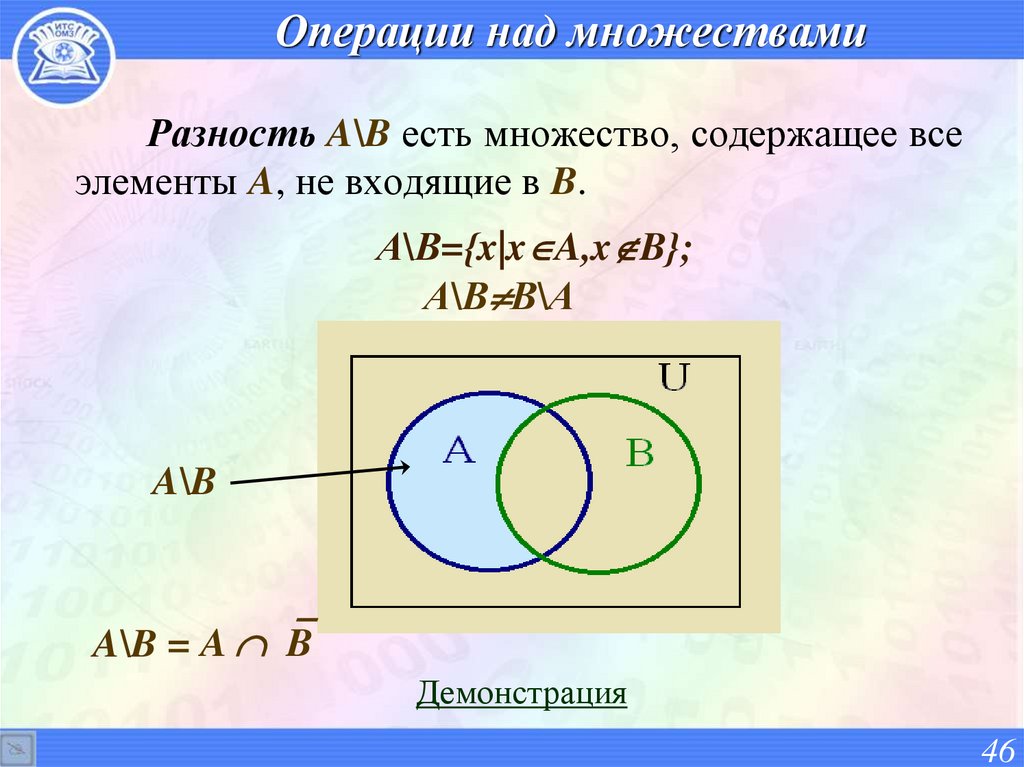
46. Операции над множествами

Разность A\B есть множество, содержащее все
элементы A, не входящие в B.
А\В={x|x A,x B};
А\В В\А
A\B
A\B = A B
Демонстрация
46

47. Операции над множествами

Пример.
Пусть даны множества:
А={a, b, m};
В={m, n, c, p}.
А \ В = {a,b}
В \ А = {n,c,p}
47

48.

48

49. Приоритет операций в алгебре множеств

Приоритет операций в алгебре множеств
следующий.
1. A
2. A B
3. A B
4. A\B
49

50. Законы алгебры множеств

1. Коммутативные законы
A B=B A
A B=B A
2. Ассоциативные законы
A (B C)=(A B) C
A (B C)=(A B) C
3. Дистрибутивные законы
A (B C)=(A B) (A C)
A (B C)=(A B) (A C)
50

51.

51

52. Приоритет операций в алгебре множеств

Пример.
Расставить
скобки
(определить
последовательность выполнения операций) в
формуле:
E=A\B A D\B
E=A\B
E=A\(B
E=(A\(B
((((( (( A)
A)
A)
D\B.
D)\B.
D))\B.
D)))\B.
52

53. Законы алгебры множеств

4. Свойства пустого и универсального множеств
A A
A U U
A U A
A
53

54. Законы алгебры множеств

5. Законы идемпотентности
A A=A
A A=A
6. Закон инволюции (двойного отрицания)
А А
7. Закон противоречия
A A
8. Закон исключенного третьего
A A U
54

55. Законы алгебры множеств

9. Закон элиминации (поглощения)
A (A B)=A
A (A B)=A
10. Законы де Моргана.
A B A B
A B A B
55

56.

56

57.

57

58.

58

59.

59

60.

60

61.

61

62. Законы алгебры множеств

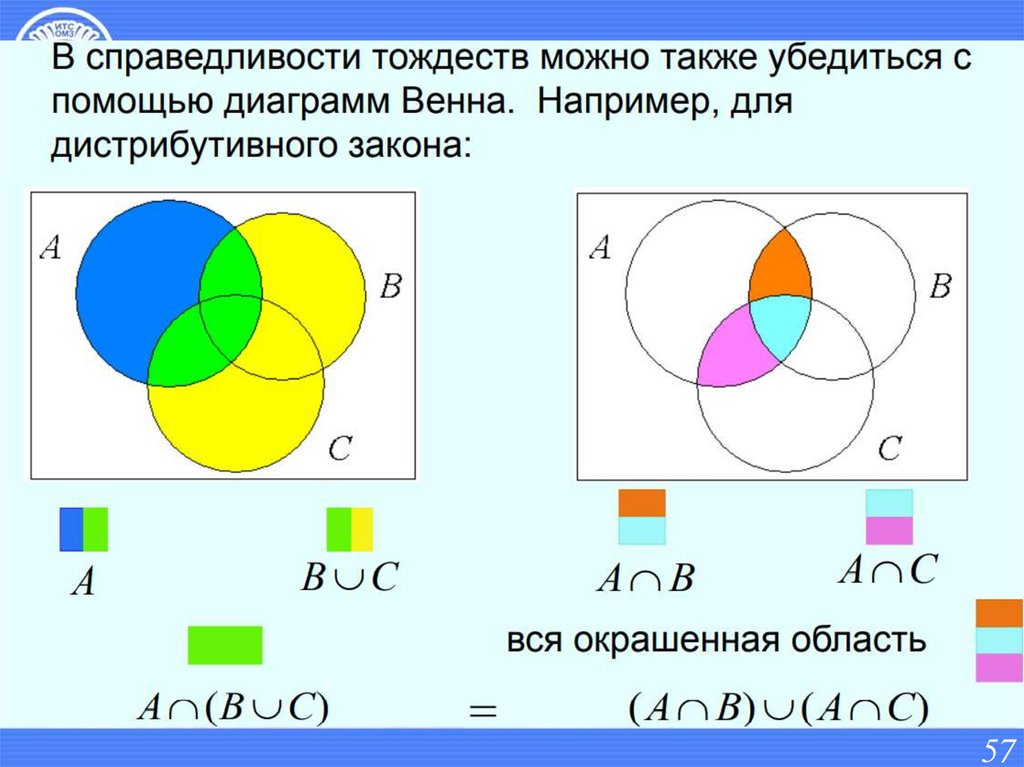
Пример.
Доказать с помощью диаграмм
дистрибутивный закон.
А (В С)=(А В) (А С).
Венна
62

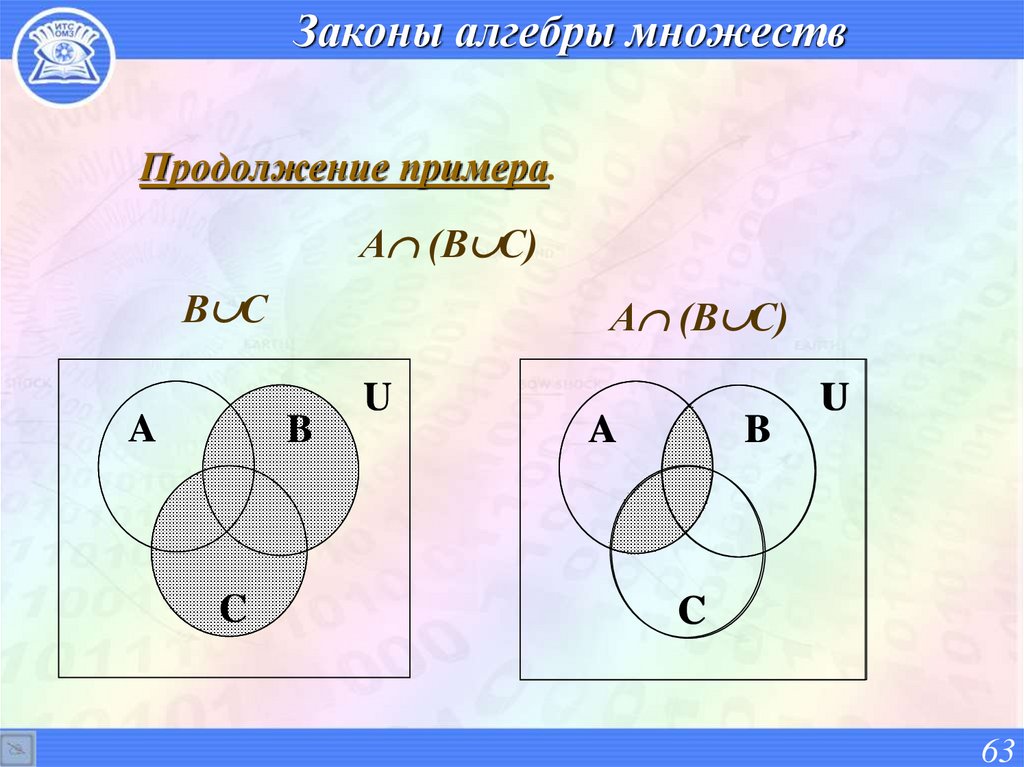
63. Законы алгебры множеств

Продолжение примера.
А (В С)
В С
A
А (В С)
B
C
U
A
B
U
C
63

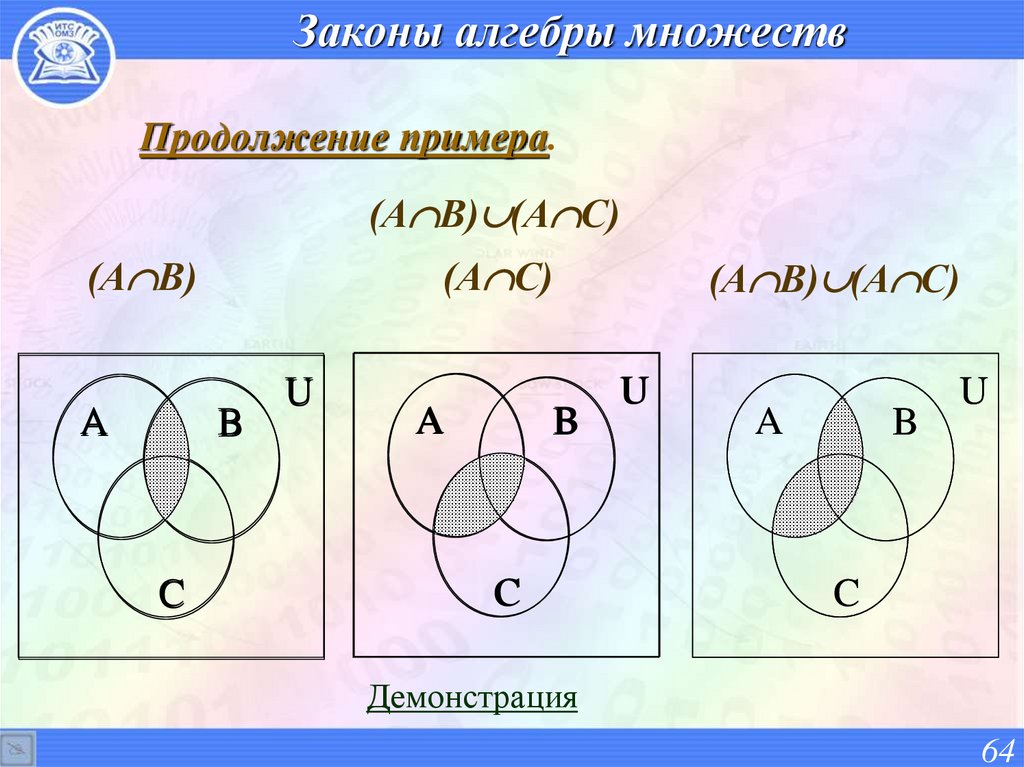
64. Законы алгебры множеств

Продолжение примера.
(А В) (А С)
(А В)
A
(А С)
B
C
U
A
B
C
(А В) (А С)
U
A
B
U
C
Демонстрация
64

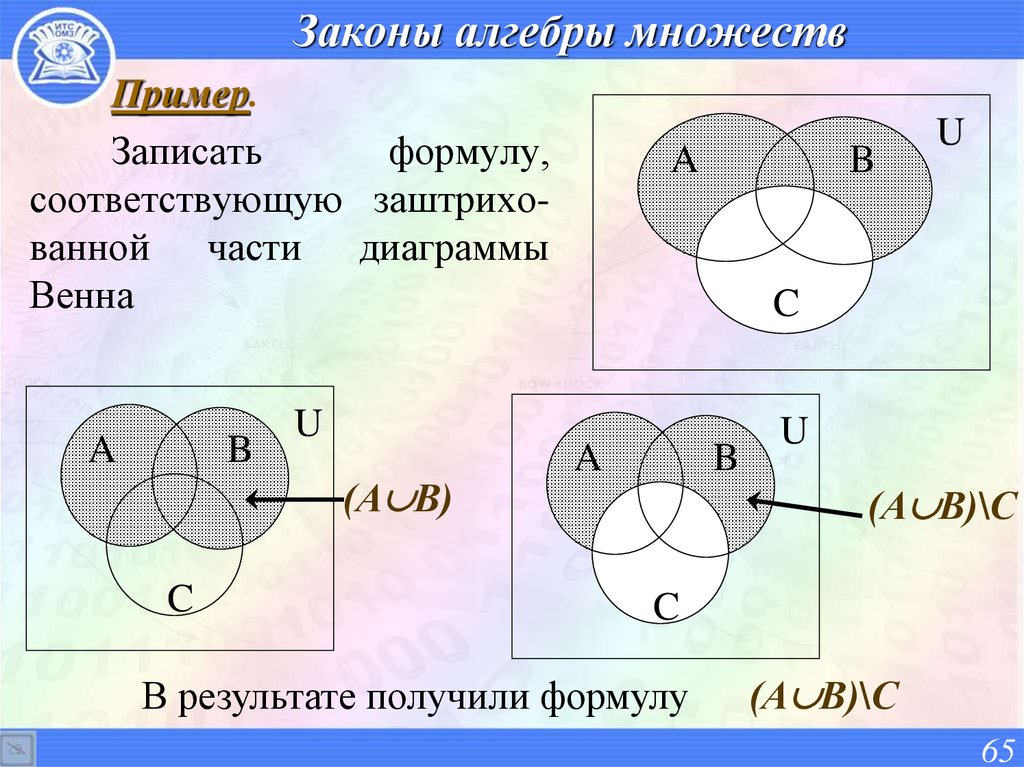
65. Законы алгебры множеств

Пример.
Записать
формулу,
соответствующую заштрихованной части диаграммы
Венна
A
B
C
U
(А В)
A
B
U
C
A
B
U
(А В)\С
C
В результате получили формулу
(А В)\С
65

66. Законы алгебры множеств

Пример.
Упростить выражение
( А В С ) ( А ( В С )) В
( А В С ) ( А ( В С )) В
А В С А В (В С )
А В С (В С )
А В С
Ответ: А В С
66

67. Бесконечные множества. Взаимно-однозначное соответствие.

Взаимно-однозначным
называется
такое
соответствие между множествами A и B, при
котором каждому элементу a A отвечает один и
только один элемент b B и каждому элементу b B
отвечает один и только один элемент a A.
Функция, определяющая взаимно-однозначное
соответствие называется биективной функцией
или биекцией.
67

68. Бесконечные множества. Эквивалентные множества.

Множества
A
и
B
называются
эквивалентными (A B), если между ними
существует биекция (хотя бы одна).
Эквивалентные
множества
называют
равномощными, что обозначается так:
|A| = |B|.
Эквивалентными друг другу оказываются
все конечные множества с одинаковым числом
элементов n (мощность каждого из этих
множеств равна n).
68

69. Бесконечные множества. Счетные множества

Множество A называется счетным, если оно
эквивалентно натуральному ряду N (A N).
С помощью биекции =N A
можно
пересчитать все элементы из A, снабдив их
индексами. Можно записать, что
A = {an}, n=1,2,…, .
69

70. Бесконечные множества. Счетные множества

Множество четных натуральных чисел
Nч={2,4,…,m,…}, всех натуральных чисел
N={1,2,…,n, …}, целых чисел Z и рациональных
чисел Q последовательно вложены:
Nч N Z Q.
Хотя для любых двух из этих множеств
нет равенства, они эквивалентны друг другу, то
есть, имеют одинаковую мощность и являются
счетными:
|Nч| = |N| = |Z| = |Q|.
70

71. Бинарные отношения на множествах

72.

• Определение.
Отношение
есть
взаимная формальная связь различных
величин, предметов, действий, то есть
элементов некоторого множества.
Отношения
в
некоторых
числовых
множествах могут выражаться
терминами:
«быть равным», «быть больше», «быть не
меньше», «быть делителем» и т.д.
Отношения во множестве
линий на
плоскости могут выражаться терминами: «быть
параллельными», «пересекаться», «касаться»
и т.д.

73.

Определение. Пара элементов (x, y), взятых в
определенном порядке, называется упорядоченной
парой.
Определение. Кортеж – это совокупность (набор)
элементов, в которой каждый элемент занимает
определенное место.
Например, множество людей, стоящих в очереди,
множество слов в предложении, множество букв в
слове, и т.п.
Длиной кортежа называется число элементов в
кортеже.
Кортежи
обычно
обозначают
последовательностью в круглых скобках (или в
угловых скобках)

74.

75.

76.

77.

78.

79.

80.

• Декартовым (прямым) произведением множеств А×В
называется множество всех упорядоченных пар (всех
кортежей), в которых первый элемент принадлежит
множеству А, а второй элемент принадлежит
множеству В.

81.

82.

83.

84.

85.

86.

87.

Подмножество R M n называется n-местным
отношением R на непустом множестве М. При
n=2 отношение R называется бинарным.
То есть бинарным отношением между
элементами множеств А и В называют любое
подмножество R множества АхВ и записывают
R АхВ.
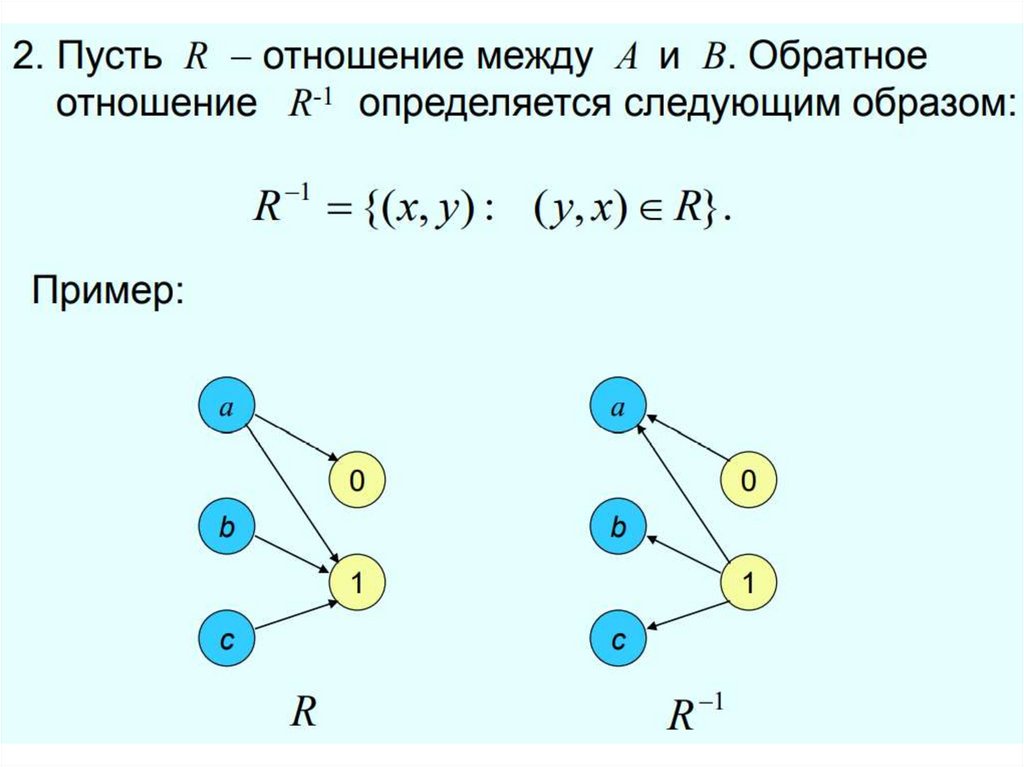
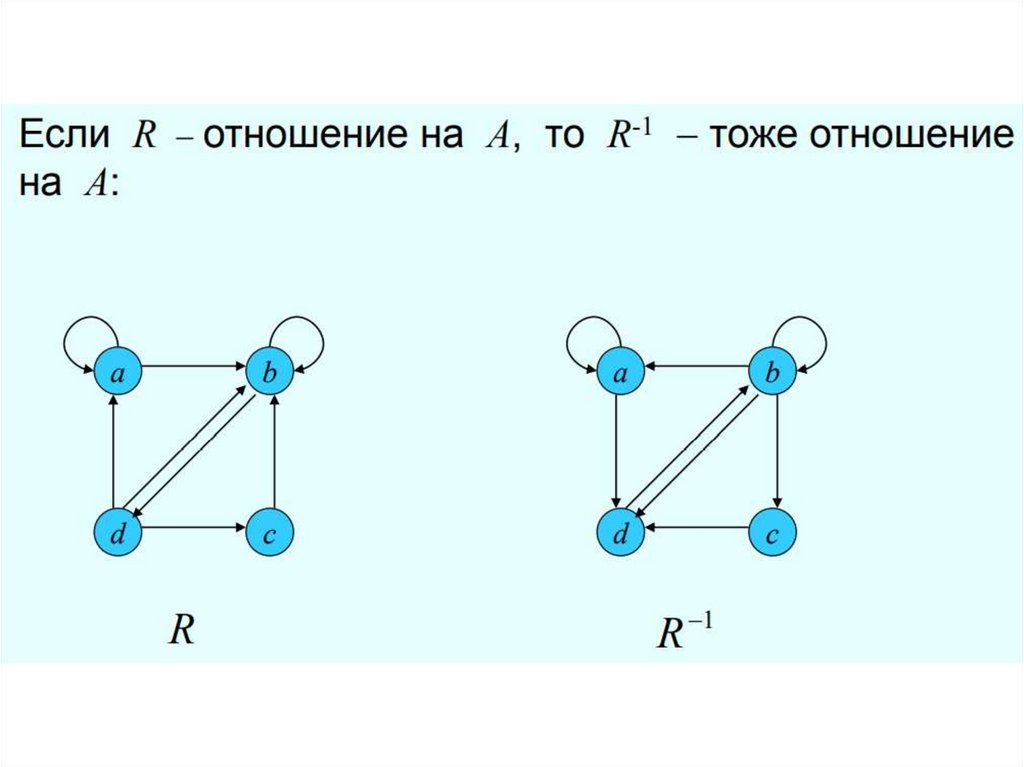
Для отношения R обратным является
отношение R-1 BxA.

88.

Способы задания бинарных отношений.
1. Перечислением элементов
V={a, b, c, d, e}, Т V2
T (a , b), (a , c), (a , d ), ( b, c), ( b, d ), ( b, e), (c, a ),
(c, b), (c, d), (c, e), (d, b), (d, c), (e, c), (d, e)}
2.
Характеристическим свойством
2
A={1, 2, 3, 4, 5}, R Z
R={(x,y) x<y}
R={(1,2), (1,3), (1,4), (1,5), (2,3), (2,4), (2,5), (3,4),
(3,5), (4,5) }
88

89.

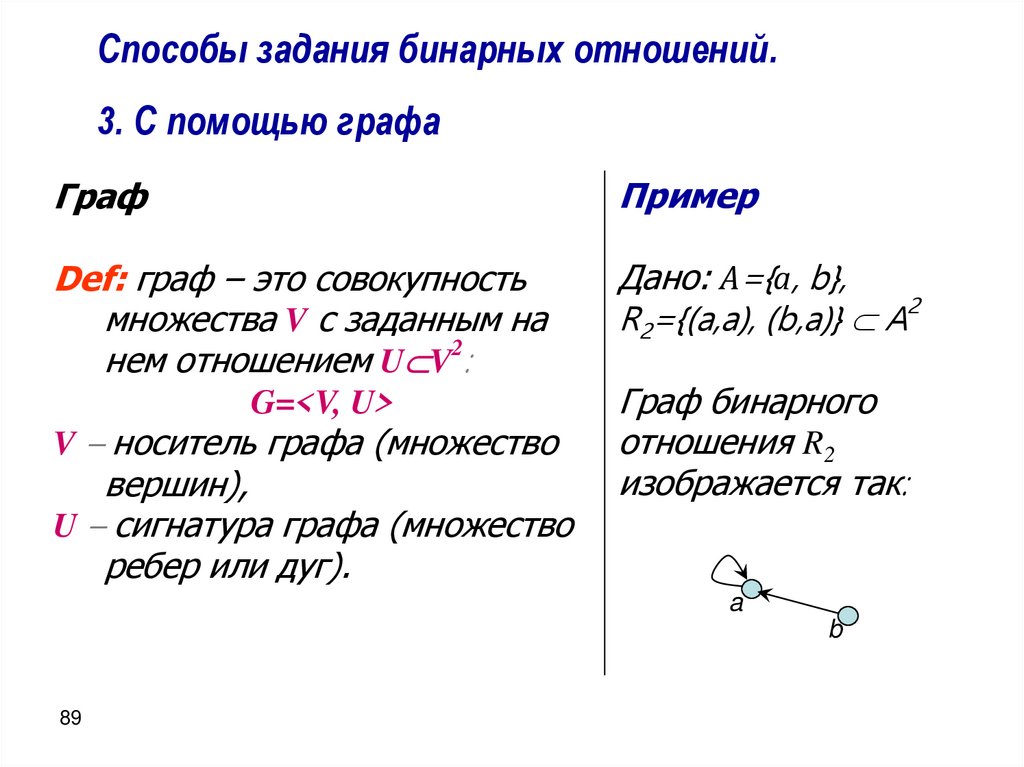
Способы задания бинарных отношений.
3. С помощью графа
Граф
Пример
Def: граф – это совокупность
множества V с заданным на
нем отношением U V2:
Дано: А={а, b},
R2={(a,a), (b,a)} A2
G=<V, U>
V – носитель графа (множество
вершин),
U – сигнатура графа (множество
ребер или дуг).
Граф бинарного
отношения R2
изображается так:
a
b
89

90.

91.

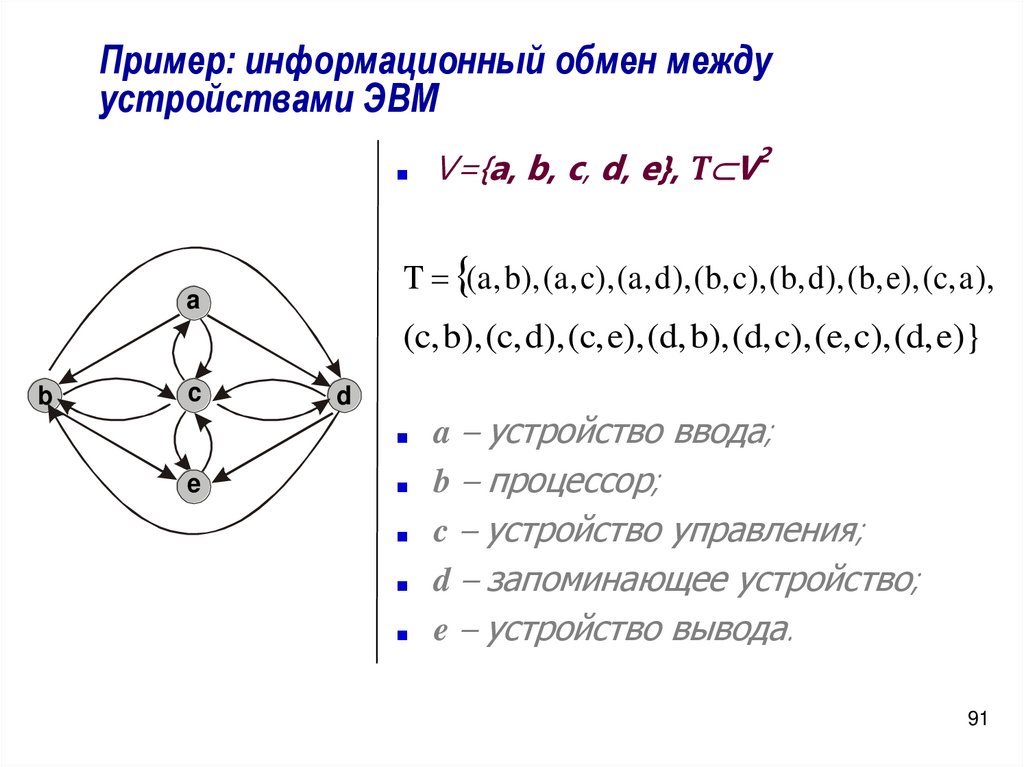
Пример: информационный обмен между
устройствами ЭВМ
V={a, b, c, d, e}, Т V2
T (a , b), (a , c), (a , d), (b, c), (b, d), (b, e), (c, a ),
a
(c, b), (c, d), (c, e), (d, b), (d, c), (e, c), (d, e)}
b
c
e
d
a – устройство ввода;
b – процессор;
c – устройство управления;
d – запоминающее устройство;
e – устройство вывода.
91

92.

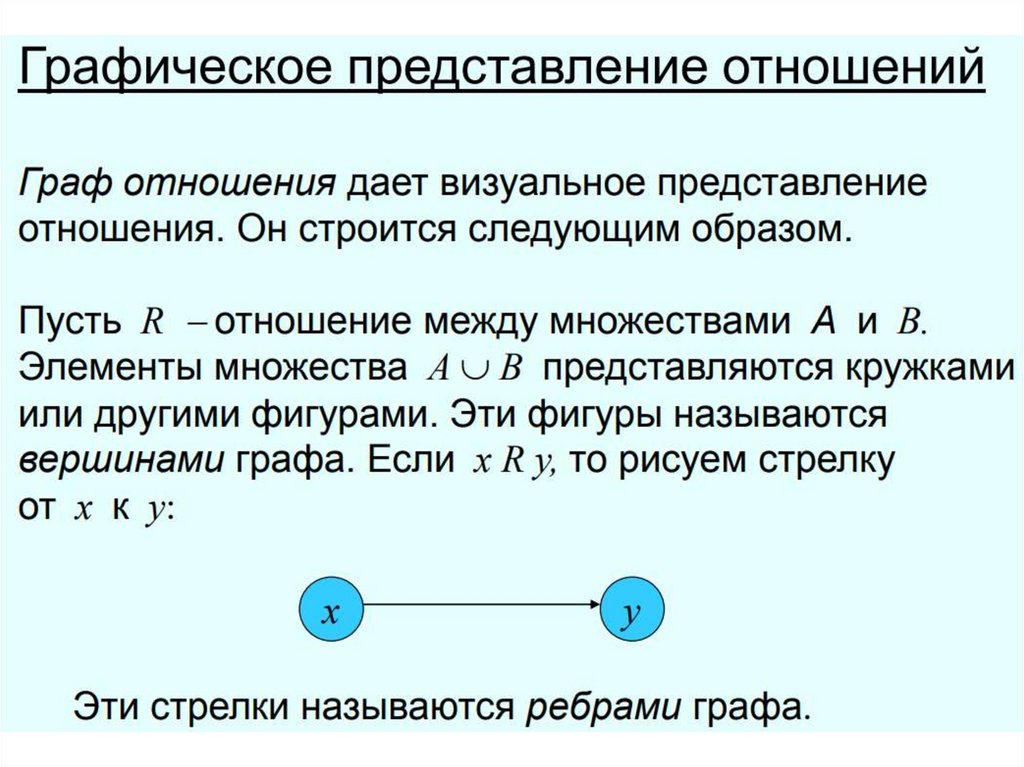
• 4. С помощью графика
Бинарное отношение R: х у
показано на рис. Заштриховано
множество точек, для координат
которых это отношение
выполняется (истинно).

93.

Способы задания бинарных отношений.
5. Матрица
Пример
Def: матрица
Дано: А={а, b},
бинарного отношения на
R2={(a,a), (b,a)} A2
множестве А={а1, а2, а3, …, an} –
это таблица размера n n,
Матрица смежности
в которой элемент cij ,
бинарного отношения
определяется следующим образом:
R представляется так:
2
1, если a i Ra j ;
cij
0 в противном случае
93
a b
a 1 0
b 1 0

94.

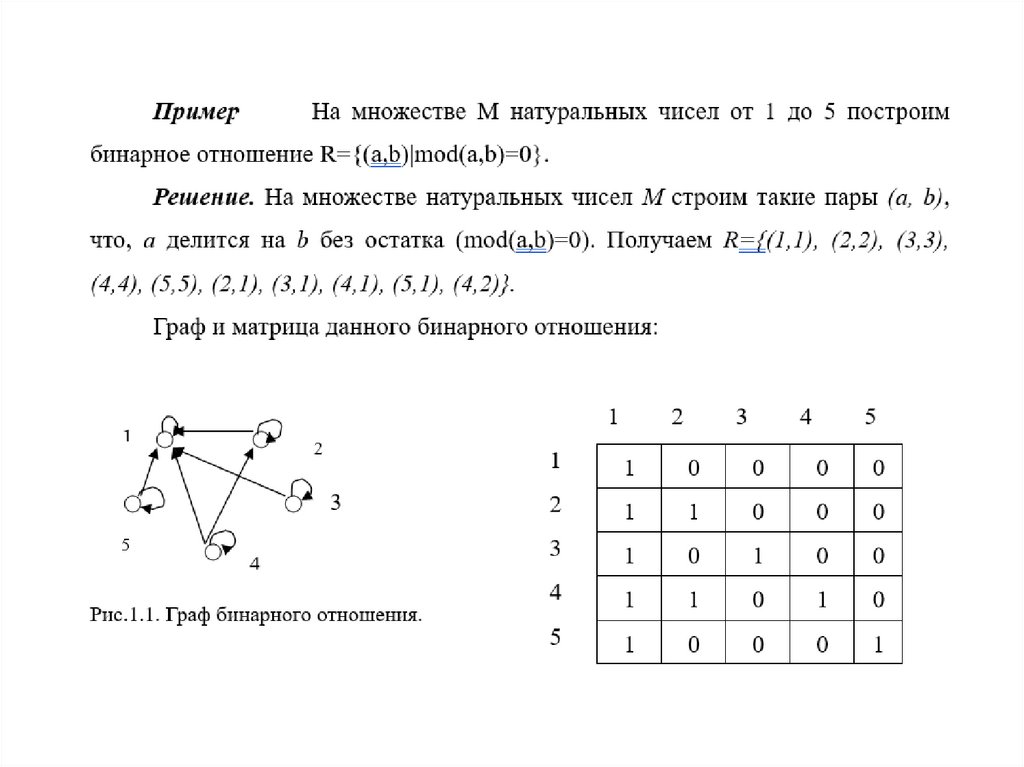
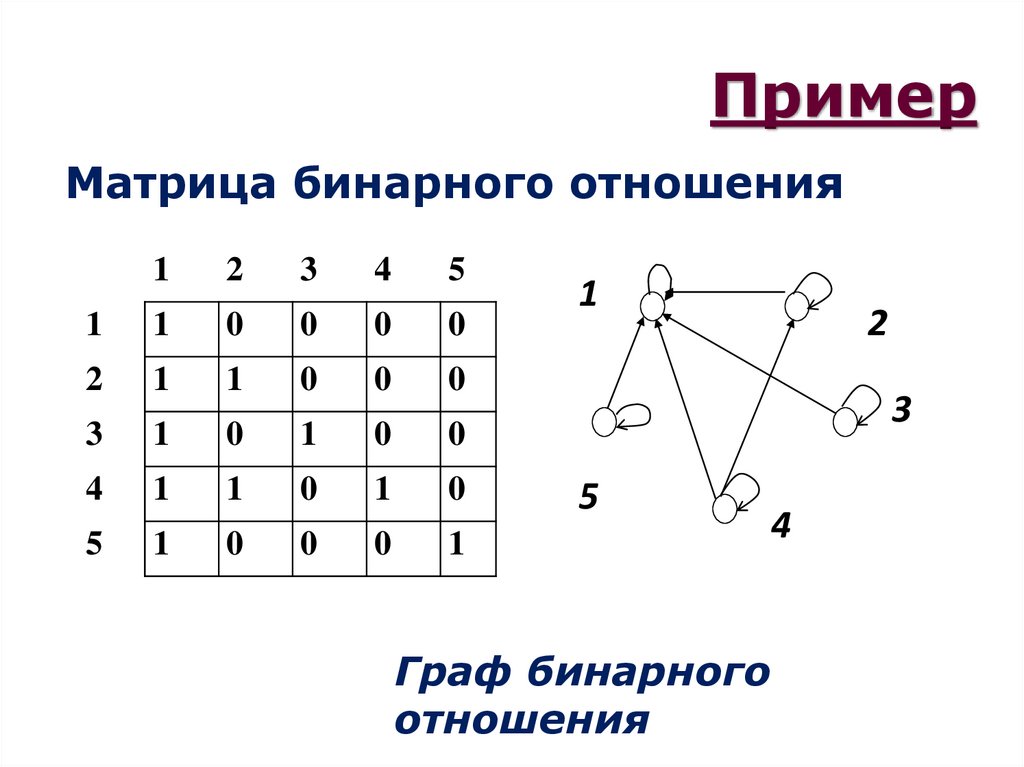
95. Пример

Матрица бинарного отношения
1
2
3
4
5
1
1
0
0
0
0
2
1
1
0
0
0
3
1
0
1
0
0
4
1
1
0
1
0
5
1
0
0
0
1
1
2
3
5
Граф бинарного
отношения
4

96.

97. Операции над бинарными отношениями

98.

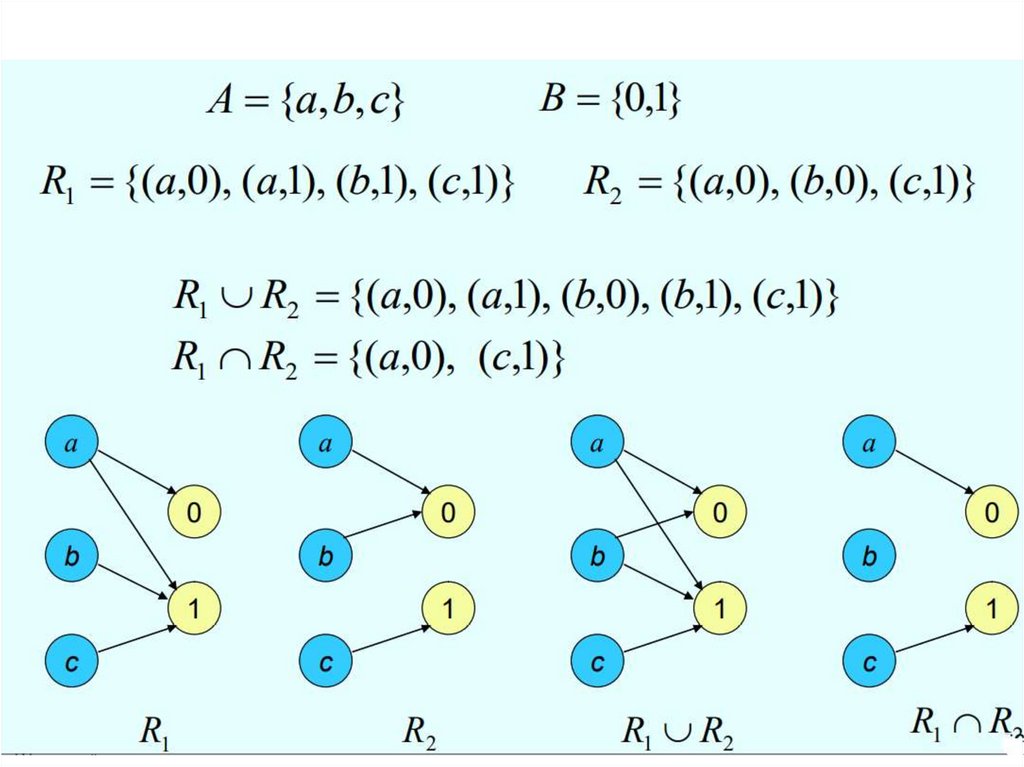
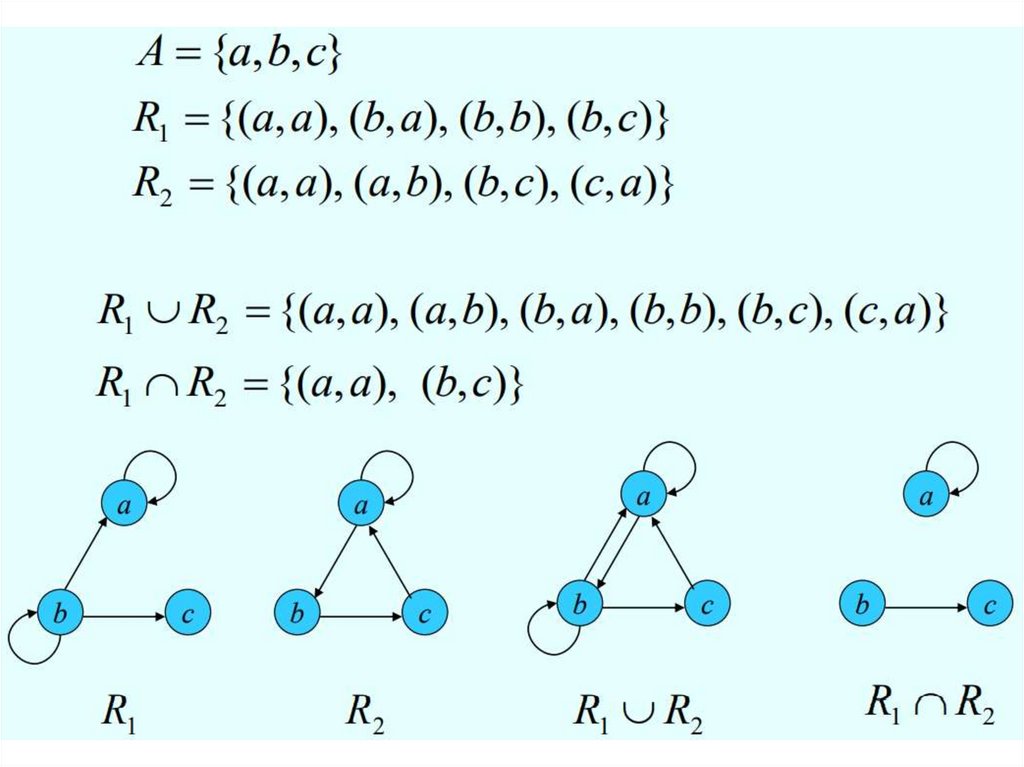
Объединени е : R1 R2 (a; b) : (a; b) R1 или (a; b) R2
Пересечение : R1 R2 (a; b) : (a; b) R1 и (a; b) R2
Разность : R1 \ R2 (a; b) : (a; b) R1 и (a; b) R2
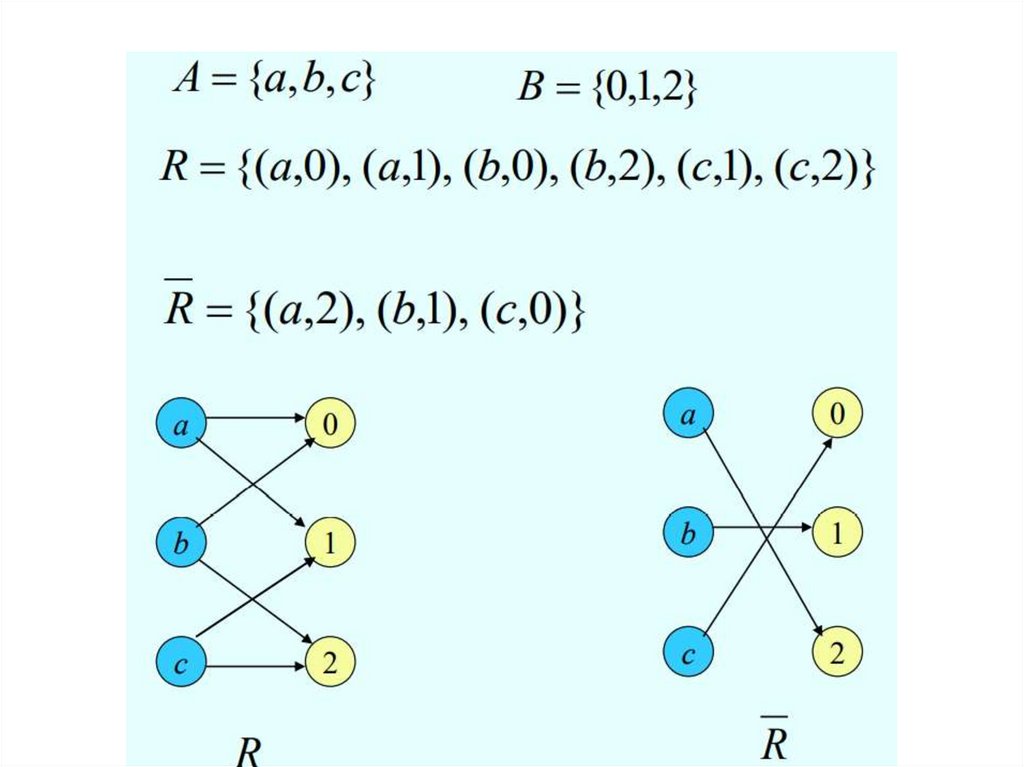
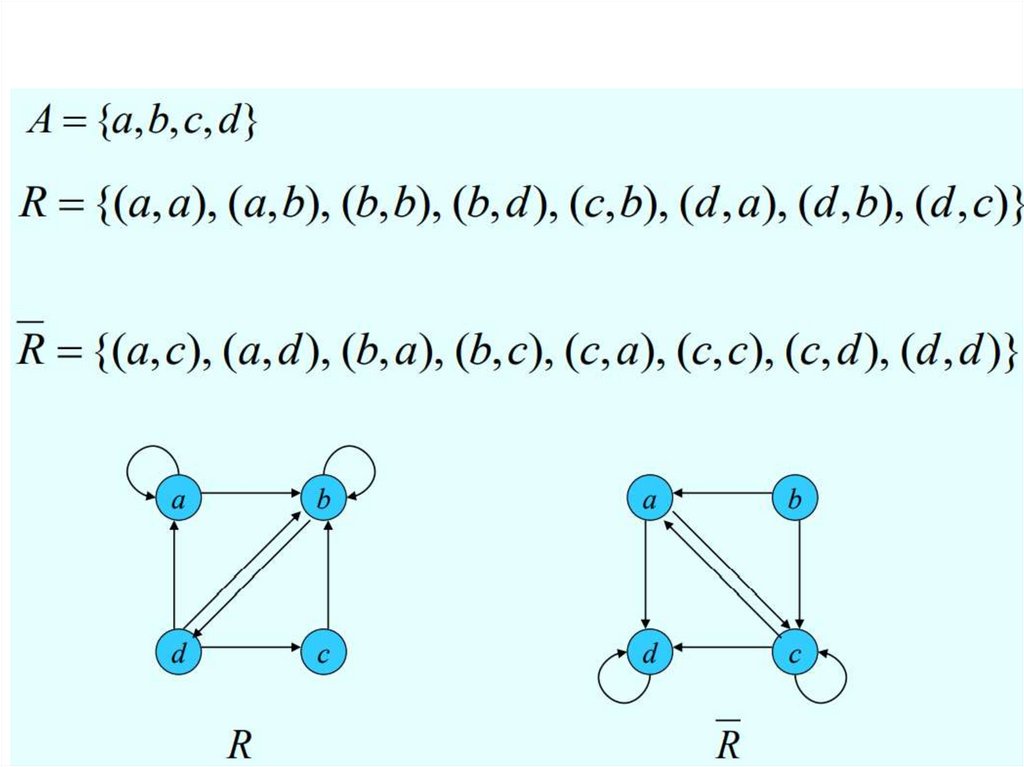
Дополнение : R U \ R
Обратное отношение : R 1 (a; b) : (b; a) R
Композиция : R R R ( 2 ) (a; c) : (a; b), (b; c) R