Similar presentations:
Множества. Лекция №1
1. Лекция №1 Множества
Ст. преподаватель:Сеитова Алия Амангалиевна
2. Содержание лекции:
о множествах и его элементах,о пустом множестве,
о способах задания множеств,
об операциях над множествами:
объединение, пересечение, разность и др.
3. Понятия теории множеств
Понятия множества и элемента множестваявляются первичными такими, как, например, точка
и прямая.
Оно было введено в математику немецким
ученым Георгом Кантором (1845-1918).Следуя
Кантору, понятие "множество" можно определить
так:
Под множеством понимается совокупность
некоторых объектов (предметов), которые
называются элементами множества.
4.
5.
Элементы множеств различны. Принятыследующие обозначения:
A, B, X,… - множества;
a, b, x, x1, x2,… - элементы множеств;
–
элемент а принадлежит А,
–
элемент b не принадлежит А;
6. Обозначения специальных множеств:
N – множество натуральных чисел;Z – множество целых чисел;
Q – множество рациональных чисел;
I – множество иррациональных чисел;
R – множество действительных чисел;
C – множество комплексных чисел;
Ø – пустое множество (не содержит ни одного
элемента).
Конечные множества состоят из конечного числа
элементов. Бесконечные – из бесконечного числа
элементов.
Например: А— множество цифр, N – множество
натуральных чисел.
7.
Основные способы задания множеств:а) перечислением элементов, например,
X={x1, x2,…, xn}, A={2,4,5,6,8,…};
б) с помощью характеристического свойства:
A={x| Р(x)}, где P(x) –свойство Р, которым обладает
элемент x, например, A = {x| x+5=3x-1}.
8.
Определения:а) множество В называется подмножеством множества А
(обозначается
), если каждый элемент множества
В является элементом множества А:
- знак включения;
б) множества А и В называют равными, если они состоят из
одних и тех же элементов:
и
в) если
и
множества А:
, то В является собственным подмножеством
- строгое включение.
9.
Заметим, что для обозначения отношения включенияприменяют как знак строгого, так и не строгого
включения, как для собственных так и для
несобственных подмножеств. И только если
требуется различить эти подмножества, различают и
эти знаки. Не следует путать знаки
и
- верно
-не верно
10.
.Множества могут быть элементами других множеств.
Множество, элементами которого являются множества,
иногда называют семейством и обычно обозначают
прописными (рукописными) буквами латинского алфавита.
Совокупность всех подмножеств множества А называется его
булеаном или множеством-степенью. Обозначается Р(А) или
2А. Таким образом, Р(А) = {B|B A}.
Булеан множества из n элементов, содержит 2n элементов
Пример. A={1,2,3},
Р(А) ={Ø,{1},{2},{3},{1,2},{1,3},{2,3}, A}.
Р(А) содержит 8 элементов, 8=23 .
11. Операции над множествами
Суммой, или объединением произвольногоконечного или бесконечного множества множеств
называется множество, состоящее из тех и только
тех элементов, которые принадлежат хотя бы
одному из множеств А,В.
Объединение множеств обозначается
А В = {x| x А или x В};
На диаграмме Эйлера-Венна объединение двух
множеств выглядит так
П р и м е р : {1,2,3} {2,3,4} = {1,2,3,4}.
12.
Пересечением или произведением любогоконечного или бесконечного множества множеств
называется множество, состоящее из тех и только
тех элементов, которые принадлежат множествам
А и В одновременно.
Пересечение множеств обозначается
А В = {x| x А и x В}
На диаграмме Эйлера-Венна пересечение двух
множеств выглядит так
Пример:
{1,2,3} {2,3,4} = {2,3}
13.
Разностью ( А \ В; А – В) между множествомA и множеством B называется множество
всех элементов из A , не являющихся
элементами из B.
Разность двух множеств обозначается
А \ В = {x| x А и x В}
На диаграмме Эйлера-Венна разность
двух множеств выглядит так
14.
Симметрическая разность или кольцеваясумма
Разность двух множеств обозначается
( , , +)
А В=(А \ В) (В \ А) = {x| (x А и x В) или (x В и x А)}
На диаграмме Эйлера-Венна разность
двух множеств выглядит так
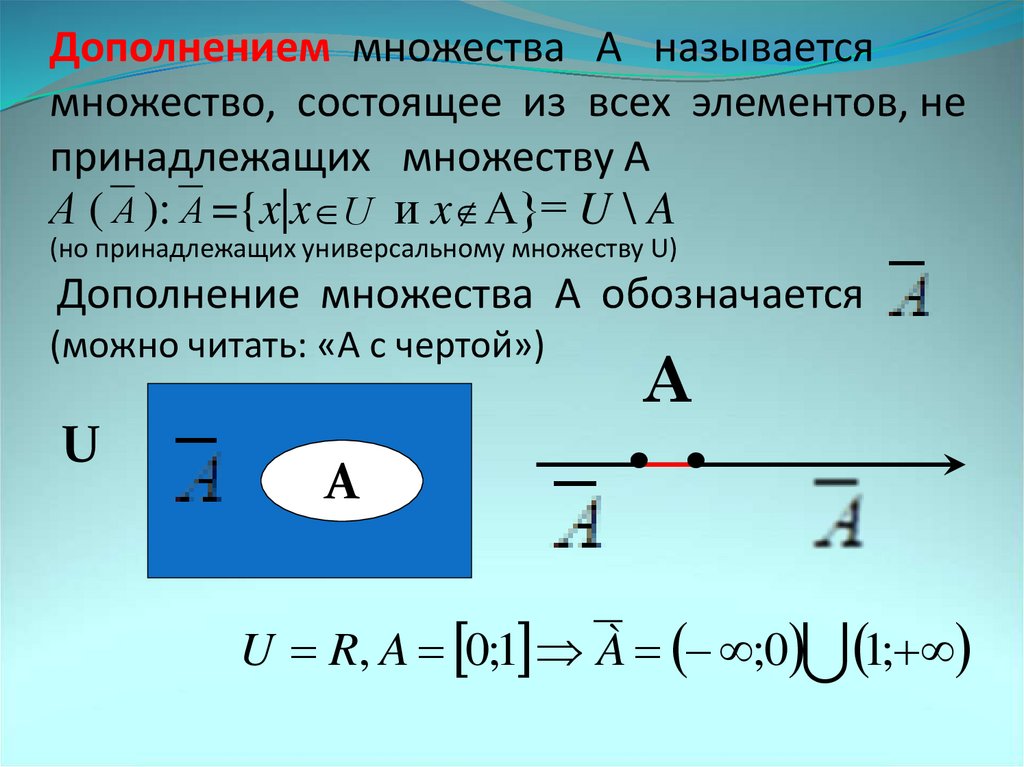
15. Дополнением множества А называется множество, состоящее из всех элементов, не принадлежащих множеству А (но принадлежащих
Дополнением множества А называетсямножество, состоящее из всех элементов, не
принадлежащих множеству А
А ( А ): А ={x|x U и x А}= U \ A
(но принадлежащих универсальному множеству U)
Дополнение множества А обозначается
(можно читать: «А с чертой»)
U
A
..
A
U R, A 0;1 À ;0 1;
16. Операции объединения и пересечения допускают обобщения:
nA1 A2 … An =
A ,
i
i 1
n
A1 A2 … An =
A .
i
i 1
17.
Прямым (декартовым) произведением множеств А и В(обозначается А×В) называется множество таких пар (a,b),
что a A и b В:
А×В = {(a,b)| a A и b В}.
18. Пример
A={1,2}, B={1,2,3}.A×B ={(1;1),(1;2),(1;3),(2;1),(2;2),(2;3)};
B×A = {(1;1),(1;2),(2;1),(2;2),(3;1),(3;2)};
A×B ≠ B×A;
A2 = {(1,1),(1,2),(2,1),(2,2)};
19. Свойства операций над множествами.
Пусть задан универсум U,тогда A, B, C U выполняются свойства:
1 Идемпотентность
А А=А
А А=А
2 Коммутативность
А В= В А
А В=В А
3 Дистрибутивность
А (В С)=( А В) ( В С)
А (В С)=( А В) ( В С)
4 Ассоциативность
А (В С)=( А В) С
А (В С)=( А В) С
5 Свойство поглощения
А (В А)=А
А (В А)=А
6 Свойство нуля и единицы (констант)
А Ø=А
А Ø= Ø
А U=U
А U= A
7 Закон де Моргана
A B=A B
A B=A B
8 Закон двойного отрицания (инволютивности)
A =A
9 Свойство дополнения
A A =U
A A = Ø
20. Контрольные вопросы:
Приведите примеры множеств.Какие бывают множества по количеству элементов?
Как обозначаются множества?
Как обозначается принадлежность или непринадлежность элемента
данному множеству?
Какими способами задаются множества (привести примеры) ?
Какие множества называются равными (привести примеры) ?
Какое множество называется подмножеством данного множества
( привести примеры и записать их символически) ?
Что называется пересечением двух множеств ( привести примеры и
записать символически ) ?
Что называется объединением двух множеств ( привести примеры и
записать символически ) ?
Что называется разностью двух множеств ( привести примеры и
записать символически ) ?
21. Литература
1. Новиков Ф.А. Дискретная математика для программистов: Учебник длявузов. 2-е изд. – СПб.: Питер, 2004. – 364 с.: ил. – (Серия «Учебник для
вузов»).
2. Андерсон, Д. Дискретная математика и комбинаторика.: Пер. с англ. – М.:
Издатель- ский дом «Вильямс», 2004. – 960 с.: ил. – Парал. тит. англ.
3. Шапорев С.Д. Дискретная математика. Курс лекций и практических
занятий. – СПб.: БХВ-Петербург, 2006.- 396 с.
4. Асеев Г.Г., Абрамов О.М., Ситников Д.Э. Дискретная математика: Учебное
пособие.- Ростов н/Д: «Феникс»6 Харьков: «Торсинг», 2003. -144 с.
5. Плотников А.Д. Дискретная математика: Учебное пособие / А.Д.Плотников.
– 2-е изд., испр. и доп. – М.: Новое знание, 2006.– 304 с.
22.
Глоссарий№
На русском языке
На английском языке
Множество
На казахском
языке
Жиын
1
2
Элемент множества
Жиын элементі
Element of the set
3
Объединение
множеств
Пересечение
множеств
Разность множеств
Жиындардың бірігуі
union of sets
Жиындардың
қиылысуы
Жиындар айырмасы
intersection of sets
симметрическая
разность
дополнение
множества
симметриялық
айырмашылық
жиынтықты
толықтыру
symmetric difference set
4
5
6
7
22
Set
difference of sets
complement of a set






















 mathematics
mathematics








