Дискретная математика. Множества и операции над ними. Тема 1

1.

Дискретная математика
Множества и операции
над ними
Наталья Викторовна
Пермякова

2.

2
Краткое содержание
1. Множества и операции над ними.
Факультет дистанционного обучения ТУСУР

3.

Основные понятия и
определения
3
Неопределяемые понятия:
1) множество
2) элемент
A – множество
3) принадлежность (∈, ∉)
a, b, c – элементы
a∈A
c∉A
Система обозначений
Заглавные буквы – множества
Строчные буквы – элементы множества
Факультет дистанционного обучения ТУСУР

4.

Основные понятия и
определения
4
Свойства множества:
1) целостность
2) различимость элементов
3) неупорядоченность
A = {a, b, a, b, c, c} – не множество
{a, b, c} = {b, c, a} – одно множество
Факультет дистанционного обучения ТУСУР

5.

Основные понятия и
определения
5
Математические символы:
⇒ – следует
⇔ – равносильно
∀ – для любого (квантор всеобщности)
∃ – существует (квантор существования)
{,} – множество элементов
{|} – множество элементов, удовлетворяющих
условию
Факультет дистанционного обучения ТУСУР

6.

Основные понятия и
определения
6
Основные числовые множества
N или ℕ - натуральные числа {1, 2, 3, …}
Z или ℤ - целые числа {… -3, -2, -1,… }
Q или ℚ - рациональные числа {m/n | m ∈ ℤ, n ∈ ℕ}
R или ℝ - действительные (вещественные) числа
C или ℂ - иррациональные числа {a+b∙i | a ∈ ℝ, b ∈ ℝ}
Факультет дистанционного обучения ТУСУР

7.

7
Внимание, вопрос
Наберите в чате последовательность единиц и нулей.
Для каждого выражения проставьте 1, если пропущен
знак ∈, 0 – если пропущен знак ∉.
1) 117 ____ ℕ;
2) 22,4 ____ ℤ;
3) 4/3 ____ ℚ;
4) 2 ____ ℚ;
5) 75 ____ℝ;
6) ____ ℤ.
Факультет дистанционного обучения ТУСУР

8.

8
Правильный ответ
1) 117 ∈ ℕ;
2) 22,4 ∉ ℤ;
3) 4/3 ∈ ℚ;
4) 2 ∉ ℚ;
5) 75 ∈ ℝ;
6) ∉ ℤ.
101010
Факультет дистанционного обучения ТУСУР

9.

9
Способы задания множеств
перечисление
элементов
A = {1, 3, 7}
характеристическое
свойство
C = {x | -1 ≤ x ≤ 7, x ∈ ℤ }
рекурсия
F = {1, 1, fi = fi-1 + fi-2, i = 3,4,5, … }
Факультет дистанционного обучения ТУСУР

10.

10
Специальные множества
Пустым множеством называется множество
, обладающее свойством:
x ∉ при любом x.
Универсальным множеством называется
множество U всех рассматриваемых в данной
задаче элементов.
Факультет дистанционного обучения ТУСУР

11.

11
Специальные множества
Пример.
Пусть U = Z и требуется найти все решения
уравнения x2 = 2.
Множество М решений этой задачи есть
пустое множество: М = .
Пусть теперь U = R.
Тогда множество М = { 2, 2 } .
Факультет дистанционного обучения ТУСУР

12.

12
Понятие включения
A B x x A x B
А - подмножество множества В
Математические символы:
- включение
- строгое включение
Факультет дистанционного обучения ТУСУР

13.

Понятие включения. Свойства
включения
1) A
13
A A
A U
3 ) A A
2) A
4) A B и B C
A C
Факультет дистанционного обучения ТУСУР

14.

14
Равенство множеств
A B
A B
A B
x x A x B ,
y y Bи y A .
A – собственное подмножество B
Пример. N Z Q R.
x x A x B ,
A B
x x B x A .
Факультет дистанционного обучения ТУСУР

15.

15
Внимание, вопрос
Какой символ используется для записи
“множество А является подмножеством
множества В”?
1)
2) U
3)
4) ∀
Факультет дистанционного обучения ТУСУР

16.

16
Диаграммы Эйлера-Венна
U
A
Универсальное множество
U
В
A
Произвольное множество
B A
Факультет дистанционного обучения ТУСУР

17.

17
Операции над множествами
Объединение множеств
A B x x A или x B
x A
x A B
x B
Пример
А = {1, 2, 3, 4}
B = {1, 2, 5}
AUB = {1, 2, 3, 4, 5}
A
3
4
1
2
5
В
U
Факультет дистанционного обучения ТУСУР

18.

18
Операции над множествами
Пересечение множеств
A B x x A и x B
x A
x A B
x B
Пример
А = {1, 2, 3, 4}
B = {1, 2, 5}
A∩B = {1, 2}
A
3
4
1
2
5
В
U
Факультет дистанционного обучения ТУСУР

19.

19
Операции над множествами
Разность множеств
A \ B x x A и x B
x A
x A \ B
x B
Пример
А = {1, 2, 3, 4}
B = {1, 2, 5}
A\B = {3, 4}
A
3
4
1
2
5
В
U
Факультет дистанционного обучения ТУСУР

20.

20
Операции над множествами
Дополнение множества
A x x A
x A x A
A
A U \ A
Пример
U = {1, 2, 3, 4, 5, 6, 7}
А = {1, 2, 3, 4}
A = {5, 6, 7}
A
3
4
1
2
5
7
6
U
Факультет дистанционного обучения ТУСУР

21.

21
Операции над множествами
Симметрическая разность множеств
A B A \ B B \ A
x A B
x A B
x A B
Пример
А = {1, 2, 3, 4}
B = {1, 2, 5}
A∆B = {3, 4, 5}
A
3
4
1
2
5
В
U
Факультет дистанционного обучения ТУСУР

22.

Операции над множествами
Пример
Приоритет операций
U 0,1, 2, 3, 4 ,
A 1, 3 , B 2, 3, 4 ,
C 0, 4
1) дополнение
2) пересечение
3) объединение
4) разность
W A \ B C A
A\ B C A
22
0,2,4 2) W C A 0,4
3 ) W В W 0,2,3,4 4 ) W A \ W 1
1) W1 A
3
2
2
3
Факультет дистанционного обучения ТУСУР

23.

23
Внимание, вопрос
Множество всех элементов, принадлежащих
одновременно и множеству А, и множеству В,
называется:
1) объединением множеств А и В;
2) пересечением множеств А и В;
3) разностью множеств А и В;
4) симметрической разностью множеств А и В.
Факультет дистанционного обучения ТУСУР

24.

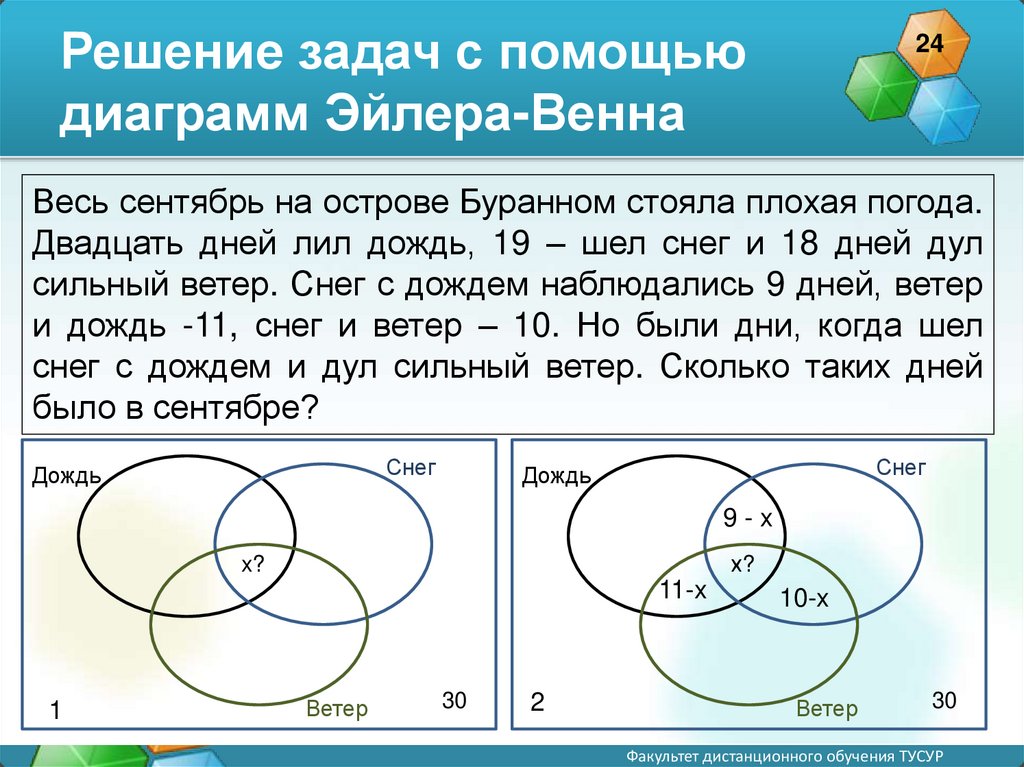
Решение задач с помощью
диаграмм Эйлера-Венна
24
Весь сентябрь на острове Буранном стояла плохая погода.
Двадцать дней лил дождь, 19 – шел снег и 18 дней дул
сильный ветер. Снег с дождем наблюдались 9 дней, ветер
и дождь -11, снег и ветер – 10. Но были дни, когда шел
снег с дождем и дул сильный ветер. Сколько таких дней
было в сентябре?
Снег
Дождь
Снег
Дождь
9-x
х?
x?
11-x
1
Ветер
30
2
10-x
Ветер
30
Факультет дистанционного обучения ТУСУР

25.

Решение задач с помощью
диаграмм Эйлера-Венна
25
Весь сентябрь на острове Буранном стояла плохая погода.
Двадцать дней лил дождь, 19 – шел снег и 18 дней дул
сильный ветер. Снег с дождем наблюдались 9 дней, ветер
и дождь -11, снег и ветер – 10. Но были дни, когда шел
снег с дождем и дул сильный ветер. Сколько таких дней
было в сентябре?
Дождь
Снег
20 – x –
(9-x) –
(11-x)
9-x
х?
11-x
3
19 – x –
(9-x) –
(10-x)
19 – x –
(9-x) –
(10-x)
9 - x + 11 - x
10-x
18 – x –
(11-x) –
(10-x)
Ветер
+
20 – x –
(9-x) –
(11-x)
30
+
18 – x –
(11-x) –
(10-x)
+ 10 - x
+
+ x = 30
19 – 9 – 10 + x + 20 – 9 -11 + x + 18 – 11 – 10 +
x + 9 – x + 11 – x + 10 – x + x = 30
19 + 20 – 9 +18 – 11 – 10 + x = 30
x=3
Факультет дистанционного обучения ТУСУР

26.

Законы алгебры множеств
№
1
2
3
4
Формула
Название
А B B A
Закон
коммутативности
А B С A B C
А B С A B C
А B С A B A C
А B С A B A C
Закон
ассоциативности
А B B A
А A
26
Закон
дистрибутивности
Закон двойного
дополнения
Факультет дистанционного обучения ТУСУР

27.

Законы алгебры множеств
№
Формула
Название
5
А A A А A A
Закон
идемпотентности
Закон де Моргана
6
А B A B А B A B
Закон поглощения
7
А A B A А A B A
А А A A A
Свойства пустого
множества
А U A А U U A A U
Свойства
универсального
множества
8
9
A\ B A B
27
A B A \ B B \ A
Факультет дистанционного обучения ТУСУР

28.

Законы алгебры множеств.
Преобразование выражений
28
Доказать равенство: A \ B \ C A \ B A C
1) A B \ C A B A C замена разности
3) A B C A B A C
2) A B C A B A C замена разности
закон де Моргана
4) A B C A B A C закон двойного отрицания
5 ) A B A C A B A C
закон дистрибутивности
Факультет дистанционного обучения ТУСУР

29.

29
Домашнее задание
1) Решение задач с помощью диаграмм
Эйлера-Венна.
2) Задачи на применение законов
алгебры множеств.
Факультет дистанционного обучения ТУСУР

30.

Спасибо за внимание!
Факультет дистанционного обучения ТУСУР