Similar presentations:
Общие понятия теории множеств. Способы задания. Основные операции над множествами и их свойства
1. Общие понятия теории множеств. Способы задания. Основные операции над множествами и их свойства
В. В. Гарбузов Воронеж: АПНОО «КВИВТ» 2023г2. 1.1. Общие понятия теории множеств
Совокупность элементов, объединённыхнекоторым признаком, свойством, составляет
понятие множество. Например, множество
книг в библиотеке, множество студентов в
группе, множество натуральных чисел N и
т.д.
Запись a M означает:
элемент
a
принадлежит множеству М, т. е. элемент a
обладает некоторым признаком. Аналогично
a M считается: элемент a не принадлежит
множеству М.
3. Изображение множеств
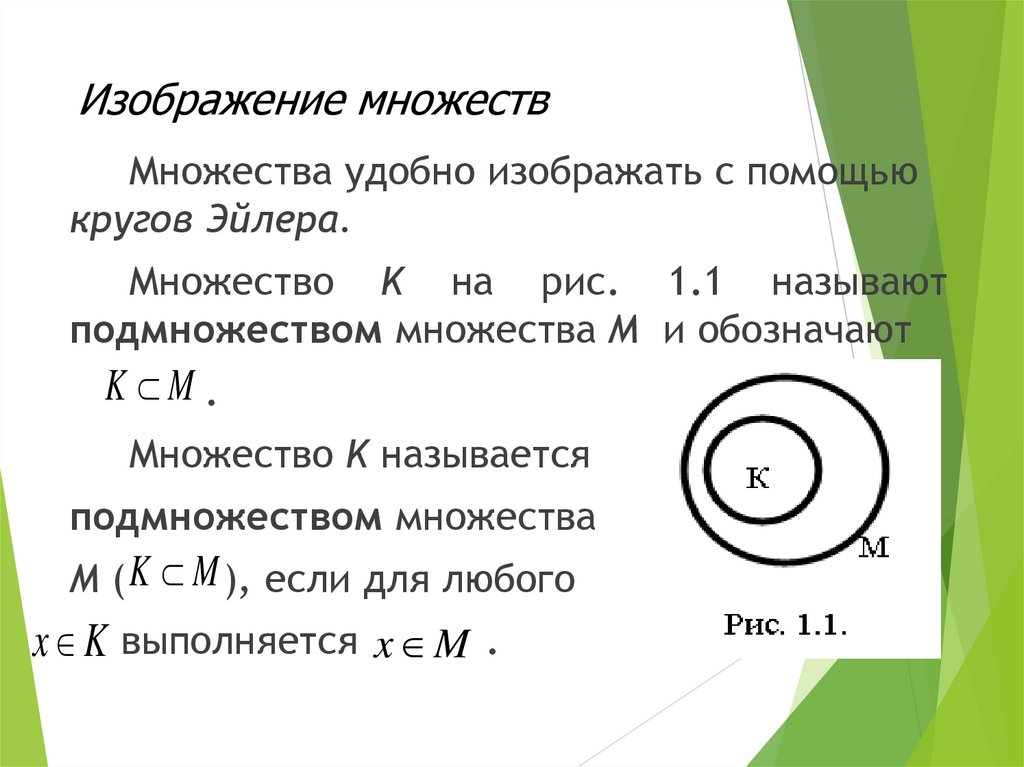
Множества удобно изображать с помощьюкругов Эйлера.
Множество K на рис. 1.1 называют
подмножеством множества М и обозначают
K M.
Множество K называется
подмножеством множества
M ( K M ), если для любого
x K выполняется x M .
4.
Универсальным называется множество U,состоящее из всех возможных элементов,
обладающих данным признаком.
Если множество не содержит элементов,
обладающих данным признаком, то оно
называется пустым и обозначается .
Равными называют два множества A и B,
состоящие из одинаковых элементов: .A B
Число элементов множества A называется
мощностью множества и обозначается A
или n A .
5.
Множество, элементами которого являютсяподмножества
множества
М,
называется
семейством множества М или булеаном этого
множества и обозначается В(М).
Мощность
булеана
множества
М
вычисляется по формуле
n
B M 2 ,
где n – это мощность множества М.
Пример.
M y, x, a , n 3, B M 23 8,
B M , y
, x
, a
, y, x
, x, a
, y, a
, y, x, a .
6.
Множество считается заданным, еслиперечислены все его элементы, или указано
свойство, которым обладают те и только те
элементы, которые принадлежат данному
множеству.
Само
свойство
называется
характеристическим.
В качестве характеристического свойства
может выступать указанная для этого
свойства порождающая процедура, которая
описывает способ получения элементов
нового множества из уже полученных
элементов или из других объектов.
7. Примеры задания множества
Множествовсех
чисел,
являющихся
неотрицательными степенями числа 2 можно
задать:
а) перечислением элементов: M 1,2,4,;8,16,32,...
2
б) указанием характеристического свойства:
M 2n 2i | i Z , i 0 ;
в) с помощью порождающей процедуры по
индуктивным правилам:
1 M 2;n
если k M 2 , то 2k .M 2
n
n
n
8. 1.2. Основные операции над множествами
Суммой или объединением двух множеств Хи Y называется множество, состоящее из
элементов, входящих или во множество Х, или
во множество Y, а может в оба множества
одновременно (рис. 1.2). Обозначение: Z X Y .
9.
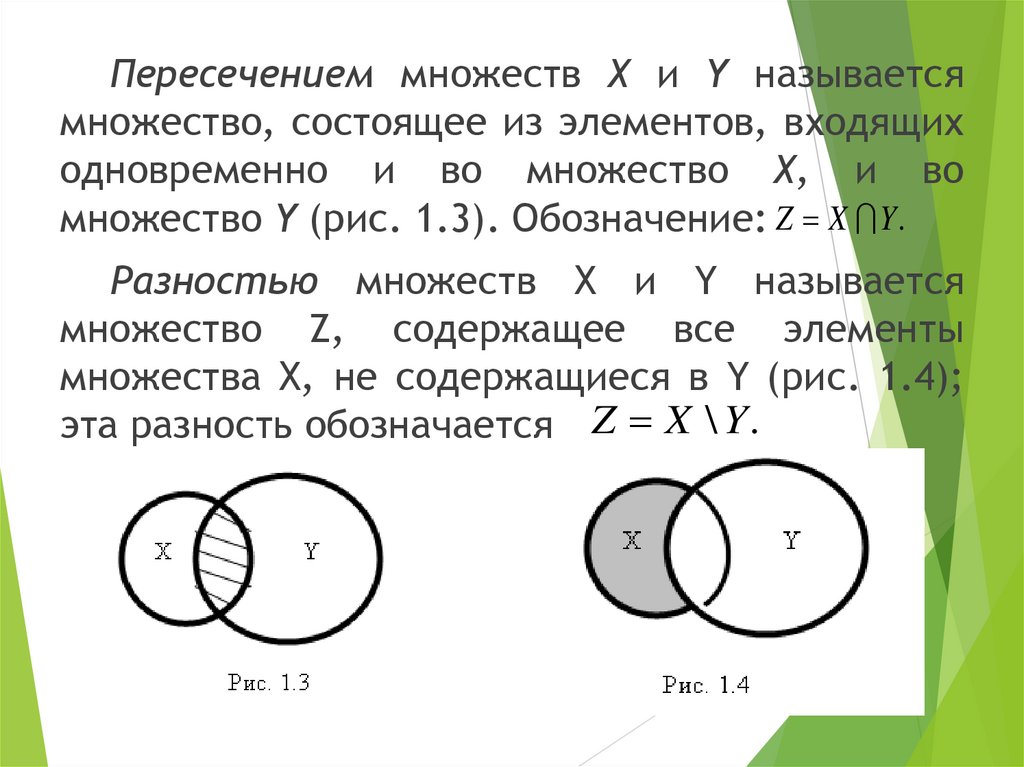
Пересечением множеств Х и Y называетсямножество, состоящее из элементов, входящих
одновременно и во множество Х, и во
множество Y (рис. 1.3). Обозначение: Z X Y .
Разностью множеств X и Y называется
множество Z, содержащее все элементы
множества X, не содержащиеся в Y (рис. 1.4);
эта разность обозначается Z X \ Y .
10.
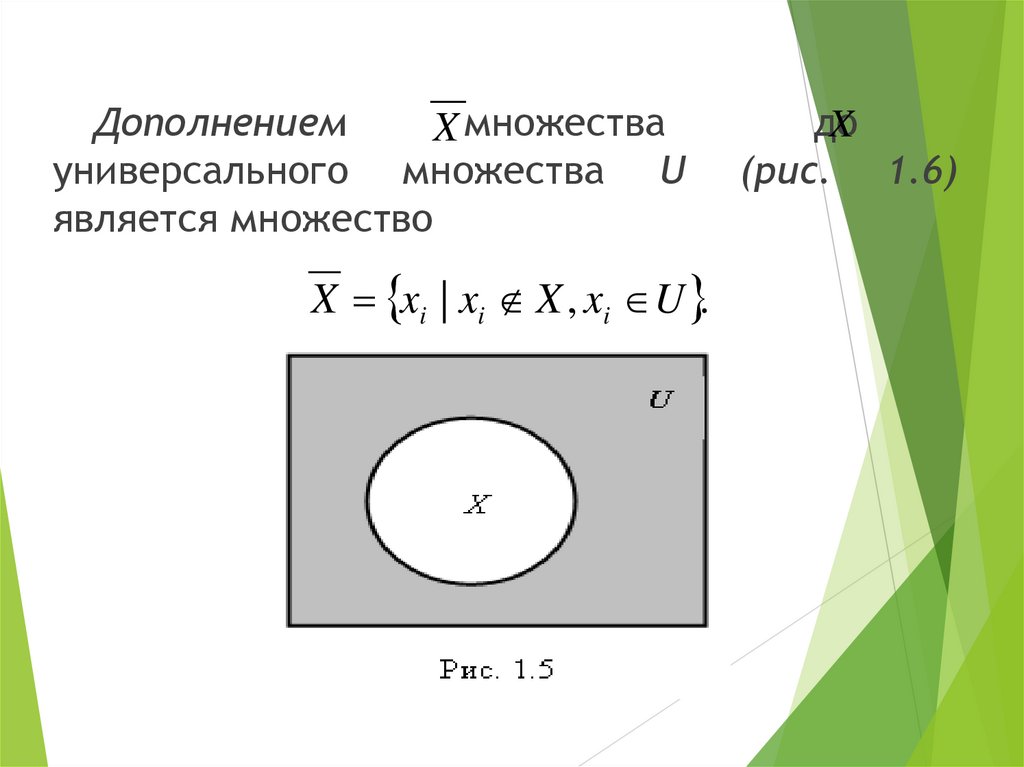
ДополнениемX множества
универсального множества U
является множество
X xi | xi X , xi U .
до
X
(рис. 1.6)
11.
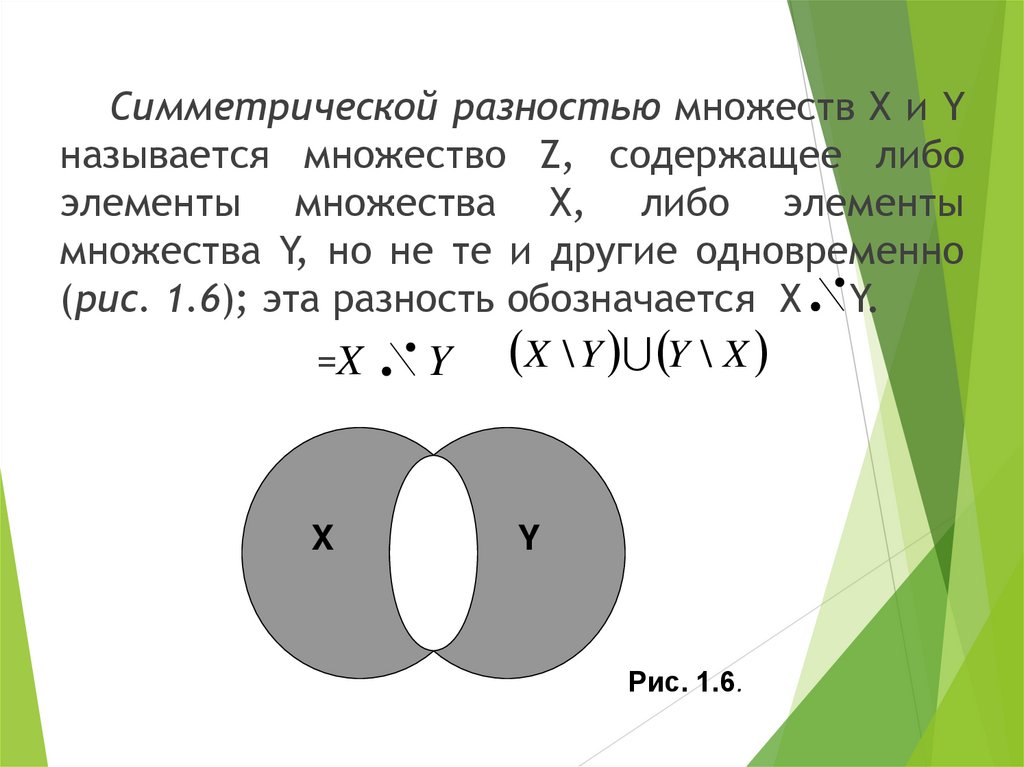
Симметрической разностью множеств X и Yназывается множество Z, содержащее либо
элементы множества X, либо элементы
множества Y, но не те и другие одновременно
(рис. 1.6); эта разность обозначается Х Y.
=X
Y X \ Y Y \ X
X
Y
Рис. 1.6.
12.
Вместо выражения«любое х из множества Х»
можно писать x X ,
где
перевёрнутая
латинская буква А взята от начала английского
слова Any – любой.
Вместо выражения
«существует элемент х из множества Х»
кратко пишут: x X ,
где
перевёрнутая
латинская буква Е является начальной в
английском слове Existence – существование.
13.
Множество A можно разбить на классы(непересекающиеся подмножества) Ai, если:
объединение всех подмножеств совпадает с
множеством A: A Ai ;
i
пересечение
любых
двух
различных
подмножеств
пусто,
т.е.
для
любых
i выполняется
j
Ai A j .
14.
Для операций над множествами справедливыследующие тождества:
законы коммутативности объединения и
пересечения
X Y Y X,
X Y Y X,
законы ассоциативности объединения и
пересечения
X Y Z Y X Z ,
X Y Z Y X Z ,
15.
законы дистрибутивности пересеченияотносительно объединения и объединения
относительно пересечения
X Y Z X Y X Z ,
законы поглощения X Y Z X Y X Z ;
X X Y X ,
законы склеивания
законы Порецкого
X X Y X ;
X Y X Y X , X Y X Y X ;
X X Y X Y,
X X Y X Y;
Операция имеет преимущество перед
операцией . Скобки - для наглядности.
16.
законы идемпотентности объединения иX X X, X X X;
законы действия с универсальным (U) и
пустым ( ) множествами
пересечения
X X,
X U U,
X ,
X U X ,
X X U,
X X ;
законы де Моргана
X Y X Y,
X Y X Y;
закон двойного дополнения
X X.












 mathematics
mathematics








