Законы распределения случайных величин. (Лекция 5)

1. Законы распределения случайных величин

1.
2.
Законы распределения дискретных
случайных величин (биномиальный,
Пуассона).
Законы распределения непрерывных
случайных величин (равномерный,
нормальный, показательный.)

2. Биномиальный закон

Дискретная случайная величина X имеет
биномиальный закон распределения, если она
принимает значения 0, 1, 2, ..., m, ..., n
с вероятностями
Pn (m) P ( X m) C p q
m
n
где p+q=1, p>0, q>0,
m
n m
,
n!
C
.
m! (n m)!
m
n

3. Биномиальный закон

Ряд распределения
xi
pi
0
1
q
n
2
…
m
Cn1 pq n 1 Cn2 p 2 q n 2 …
Cnm p m q n m …
n
причем
p
…
i
n
pn
1
0
02.05.16
Ирина Юрьевна Хар
3

4. Биномиальный закон

n, p
Параметры
Математическое ожидание
M ( X ) np
Дисперсия
D( X ) npq
Среднее квадратическое
отклонение
Мода
(наивероятнейшее число)
( X ) npq
02.05.16
np q Mo( X ) np p
Ирина Юрьевна Хар
4

5. многоугольники (полигоны) распределения случайной величины X, имеющей биномиальный закон распределения с параметрами n=5 и p (для  p=0,2; 0,3; 0,5; 0

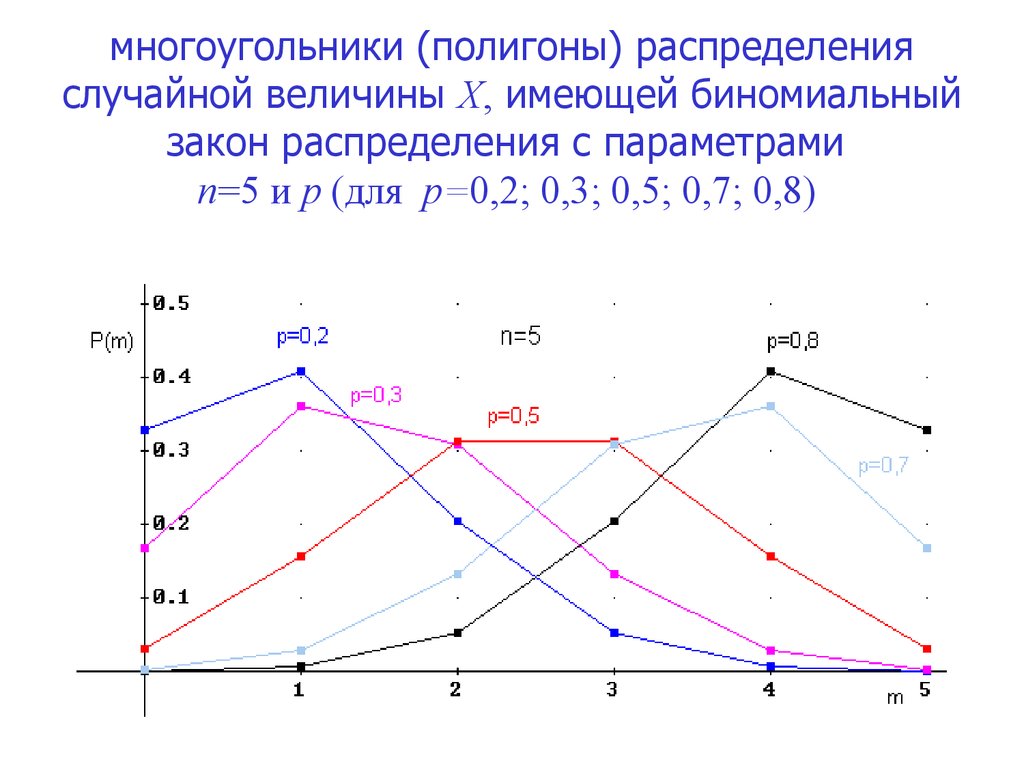
многоугольники (полигоны) распределения
случайной величины X, имеющей биномиальный
закон распределения с параметрами
n=5 и p (для p=0,2; 0,3; 0,5; 0,7; 0,8)

6. Пример

Примерно 20%
судебных дел – это дела
по обвинению в краже.
В порядке
прокурорского надзора
проверено 4 наудачу
отобранных дела.
Каково наивероятнейшее значение дел о краже среди
отобранных и какова вероятность этого значения?

7.

n 4,
20
p
0,2,
100
РЕШЕНИЕ
q 1 0,2 0,8
np q Mo( X ) np p
4 0,2 0,8 Mo( X ) 4 0,2 0,2
0 Mo( X ) 1
m1 0, m2 1

8.

РЕШЕНИЕ
m1 0, m2 1
P4 (0) 0,8 0,4096
4
P4 (1) C 0,2 0,8 0,4096
1
4
1
3

9. Закон Пуассона

Дискретная случайная величина X имеет закон
распределения Пуассона, если она
принимает значения 0, 1, 2, ..., m, ...
(бесконечное, но счётное множество значений) с
вероятностями
m
a a
P ( Х m)
e ,
m!
е = 2,71828...

10. Закон Пуассона

Ряд распределения
xi
pi
0
e
a
1
2
a e
a 2 e a
…
2
a
…
m
…
a m e a …
m!
pi 1
причем
0
02.05.16
Ирина Юрьевна Хар
10

11. Закон Пуассона

Параметры
а
Математическое
ожидание
M(X ) a
Дисперсия
D( X ) a
Среднее
(X) a
квадратическое
отклонение
Мода
a 1 Mo( X ) a
(наивероятнейшее
число) Ирина Юрьевна Хар
02.05.16
11

12. Многоугольники распределения случайной величины X, имеющей закон распределения Пуассона с параметром  a (для a=0,5; 1; 2; 3,5; 5).

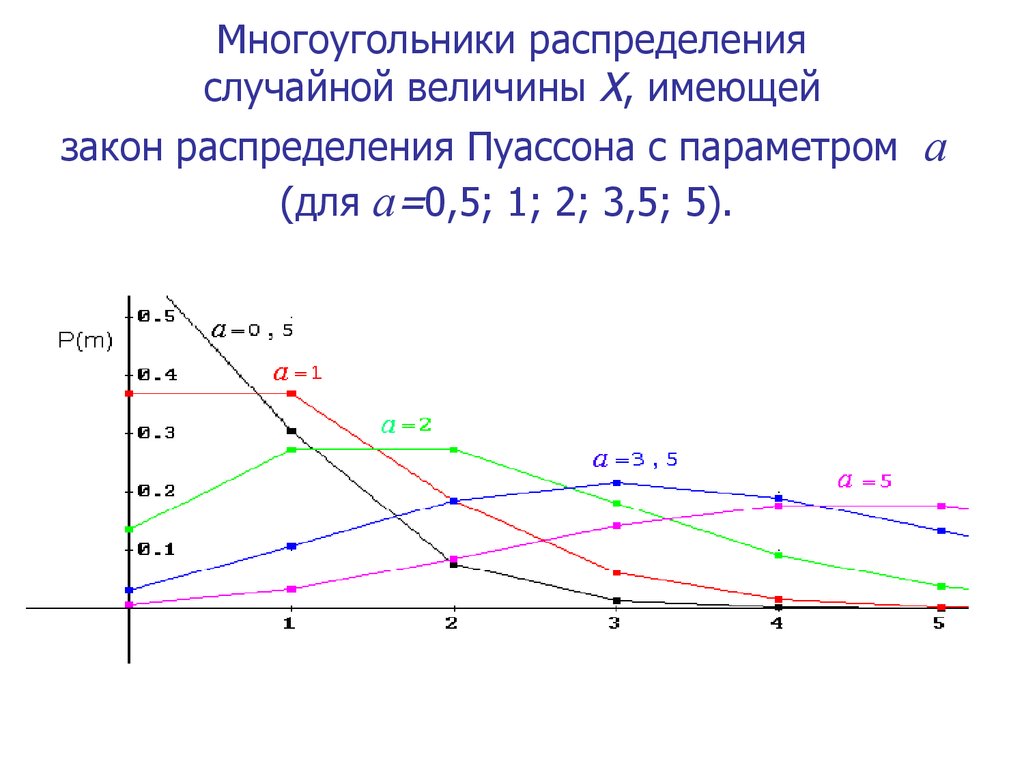
Многоугольники распределения
случайной величины X, имеющей
закон распределения Пуассона с параметром a
(для a=0,5; 1; 2; 3,5; 5).

13.

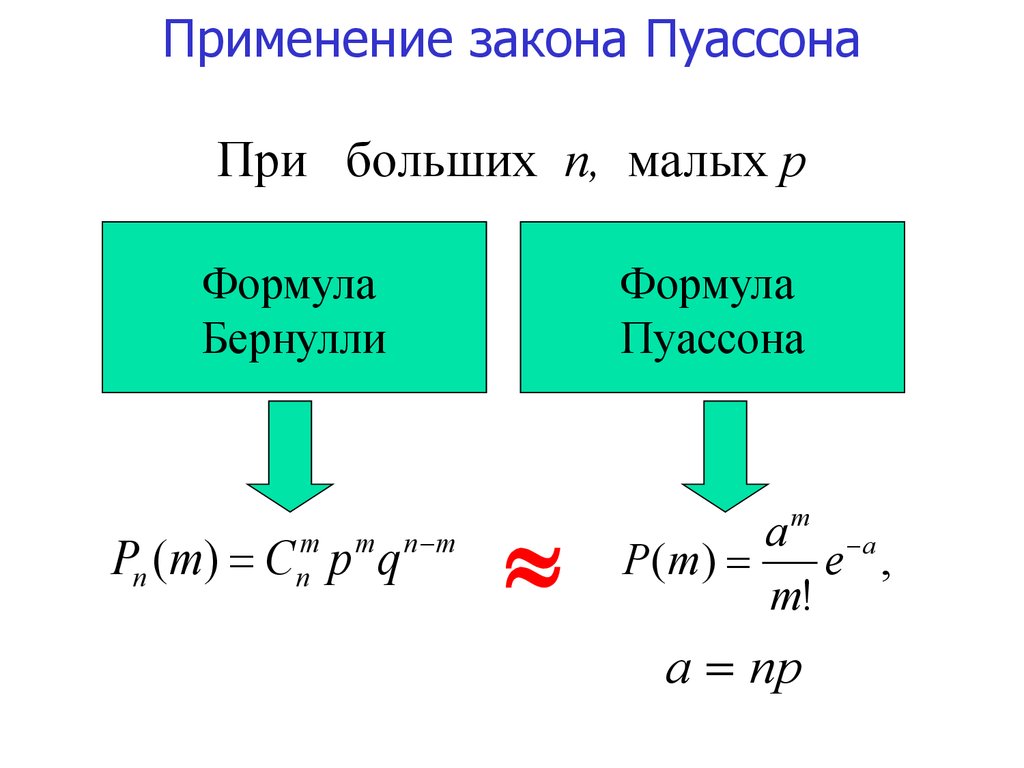
Применение закона Пуассона
При больших n, малых р
Формула
Бернулли
Pn (m) Cnm p m q n m
Формула
Пуассона
a m a
P ( m)
e ,
m!
a np

14. Пример

Примерно 0,1%
судебных дел – это дела
по обвинению в
убийстве. Проверено
200 наудачу взятых
судебных дел.
Какова вероятность того, что среди них
дел о убийстве буде: 0, 1, 2, 3 ?

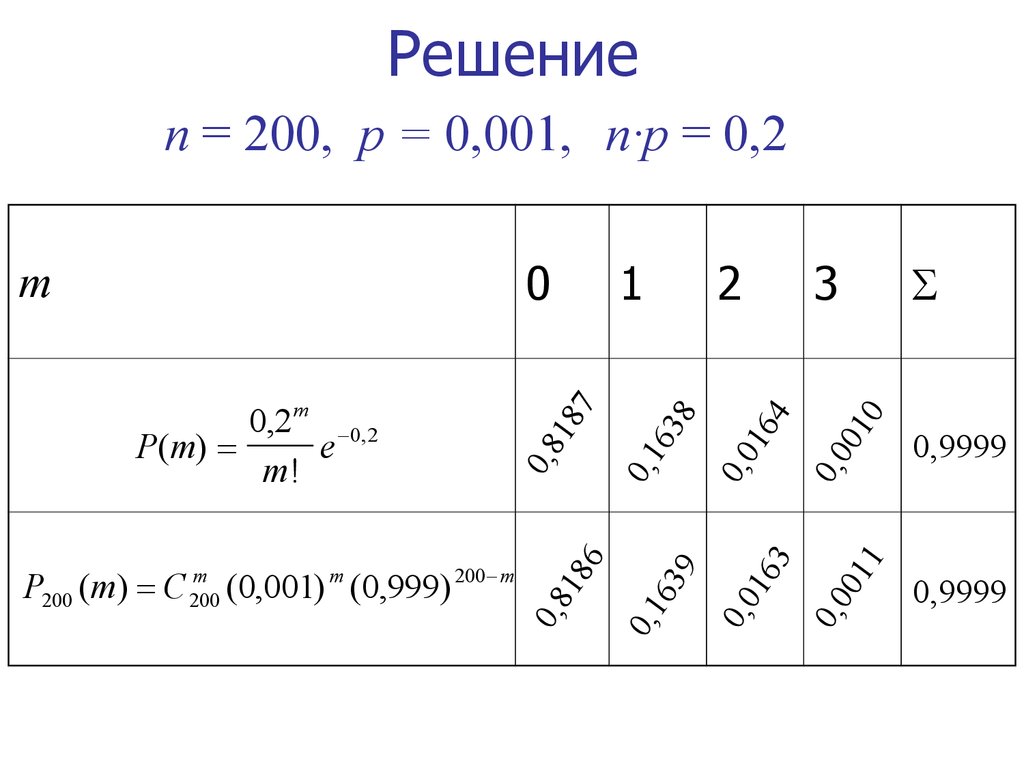
15. Решение

n = 200, p = 0,001, n·p = 0,2
3
0,0
16
3
0,9999
9
0,9999
0,0
01
1
2
0,1
63
8
0,0
16
4
0,0
01
0
87
0,8
1
m
P200 (m) C 200
(0,001) m (0,999) 200 m
0,8
18
6
0,2 m 0,2
P(m)
e
m!
1
0,1
63
0
m

16. Вероятности того, что за промежуток времени длиной t наступит m событий простейшего потока

Применение закона Пуассона
Вероятности того, что за промежуток времени
длиной t наступит m событий простейшего потока
mm
( at ) a t
ee ,
PPt t((mm))
a m
! t
a t
– это среднее число a
событий
tпотока,
происходящих в единицу времени (интенсивность).
a t
a t

17. Пример

В дежурную часть
органов внутренних дел
за час в среднем
поступает 30
сообщений различного
характера.
Какова вероятность, что за минуту поступит 2
сообщения?

18. Решение

Количество сообщений, поступающих в час = 30,
1
t = 1(мин) = 1/60 (час), a 30 0,5
60
2
0,5 0,5
P1 мин. (2)
e 0,07
2

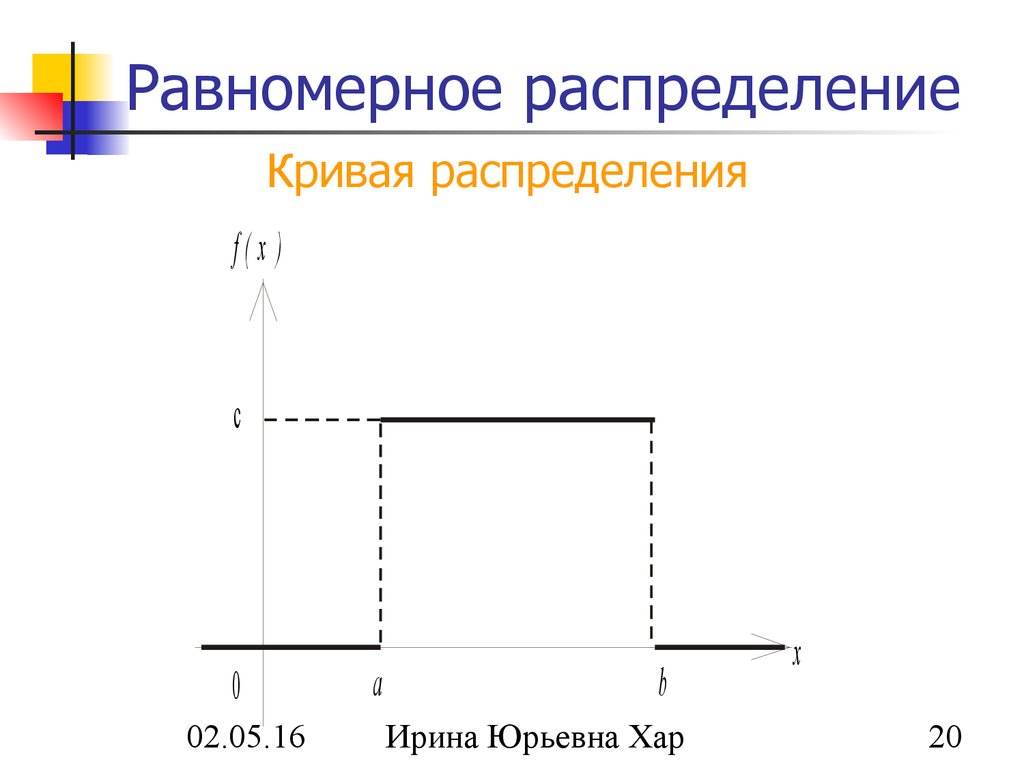
19. Равномерный закон

Непрерывная случайная величина Х имеет
равномерное распределение на отрезке [a, b], если
на этом отрезке плотность распределения вероятности
случайной величины постоянна, а вне его равна нулю,
т.е. если
х a,
0 при
f ( x ) c при a x b,
0 при
x b.
1
const .
где c
b a

20. Равномерное распределение

Кривая распределения
f(x )
c
0
02.05.16
a
b
Ирина Юрьевна Хар
x
20

21. Равномерный закон

Математическое
ожидание
b a
M(X)
2
Дисперсия
(b a ) 2
D( X )
12
Среднее квадратическое
отклонение
b a
(X)
2 3
Вероятность попадания
СВ Х в интервал [ , ],
([ , ] [a, b])
02.05.16
P( X )
b a
Ирина Юрьевна Хар
21

22. Пример

Цена деления шкалы
амперметра равна 0,1 А.
Показания округляют до
ближайшего целого
деления.
Найти вероятность того, что при отсчете будет
сделана ошибка, превышающая 0,02 А.

23. Решение

0
0 ,0 1
0 ,0 2 0 ,0 3
0 ,0 4
0 ,0 5
0 ,0 6 0 ,0 7
0 ,0 8 0 ,0 9
Ошибка превысит заданную точность, если
Х [0,02, 0,08]
0,08 0,02
P (0,02 X 0,08)
0,6
0,1
0 ,1

24. Нормальный закон

Непрерывная случайная величина Х имеет
нормальное распределение, если плотность
вероятности f(x) имеет вид:
1
f ( x)
e
2
( x a )2
2 2

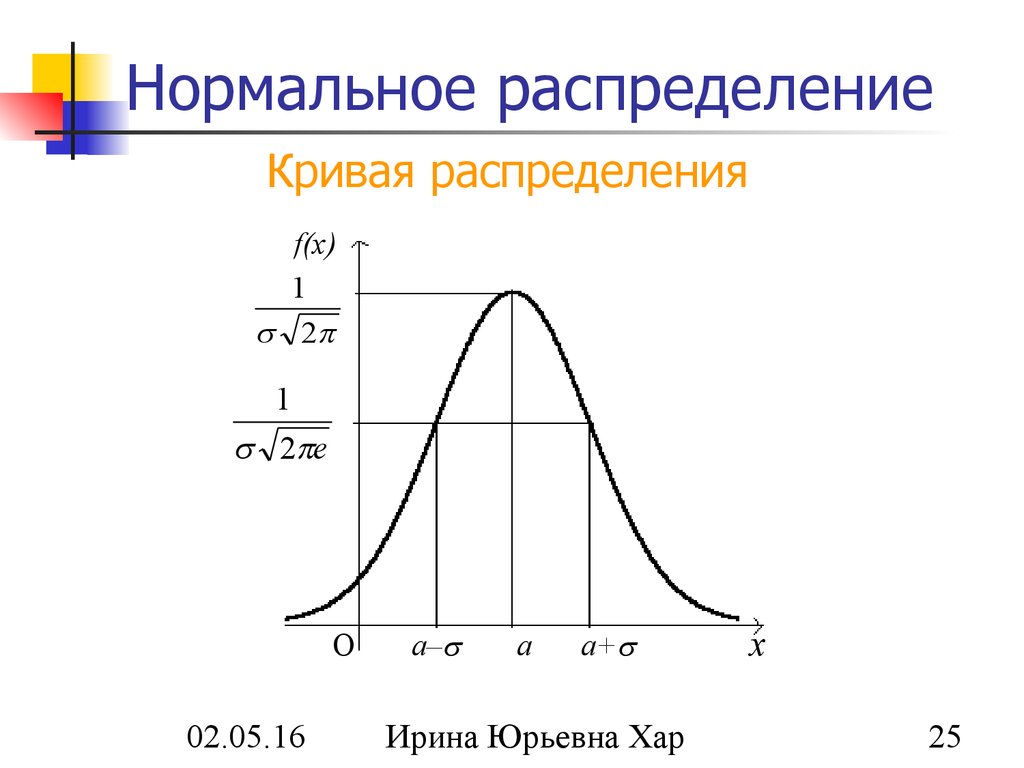
25. Нормальное распределение

Кривая распределения
f(x)
1
2
1
2 e
O
02.05.16
a–
a
a+
Ирина Юрьевна Хар
x
25

26. Нормальный закон

Параметры
Математическое
ожидание
Дисперсия
Среднее квадратическое
отклонение
а,
M(X ) a
D( X )
2
(X )
Вероятность попадания
a
a
P( X ) Ф
Ф
,
СВ Х в интервал [ , ],
Ф(х) –Хар
функция Лапласа
([ , ] [a,02.05.16
b])
Ирина Юрьевна
26

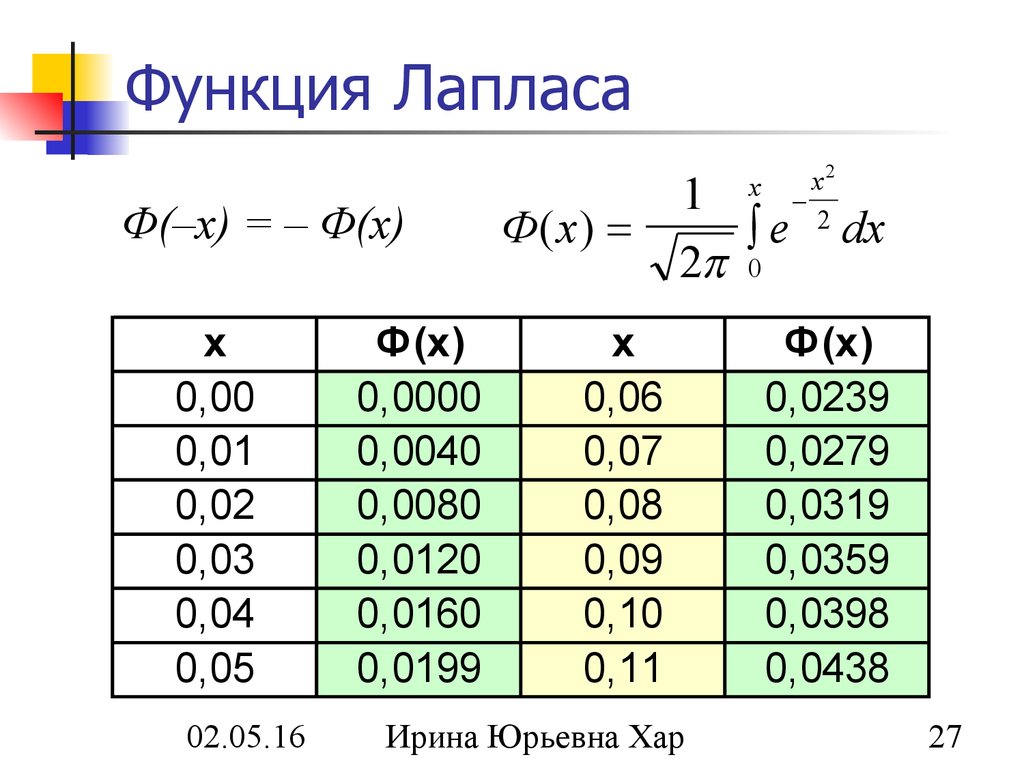
27. Функция Лапласа

Ф(–х) = – Ф(х)
x
0,00
0,01
0,02
0,03
0,04
0,05
02.05.16
Ф(х)
0,0000
0,0040
0,0080
0,0120
0,0160
0,0199
Ф( x )
1
e
2 0
x
0,06
0,07
0,08
0,09
0,10
0,11
Ирина Юрьевна Хар
x
x2
2
dx
Ф(х)
0,0239
0,0279
0,0319
0,0359
0,0398
0,0438
27

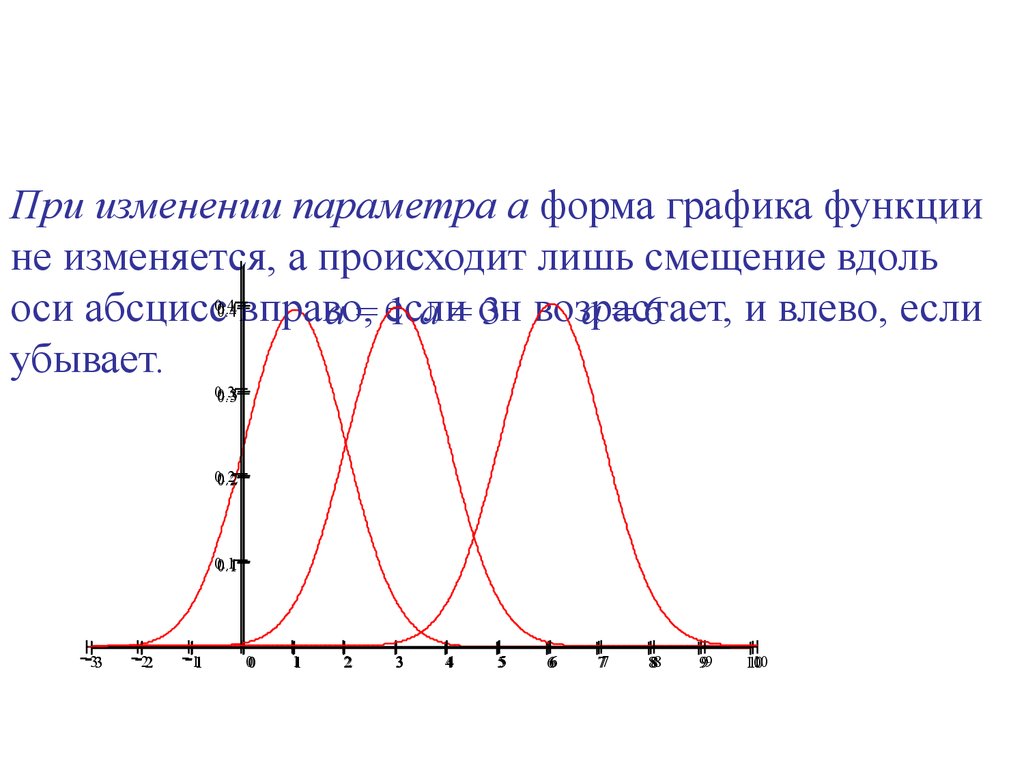
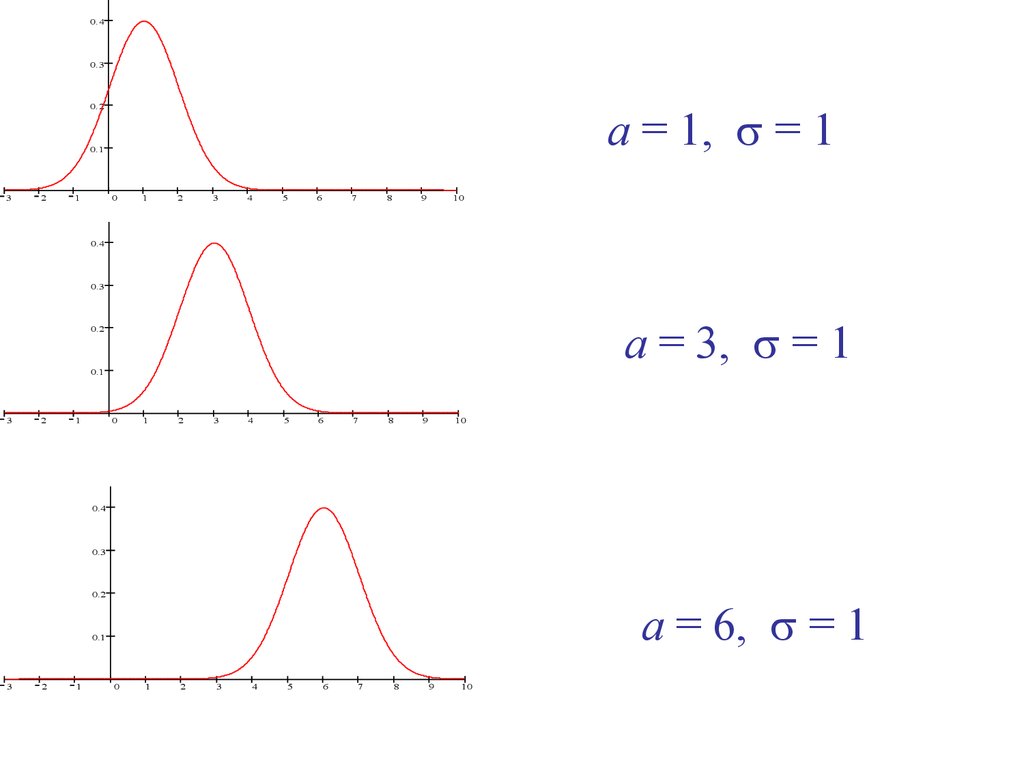
28. При изменении параметра а форма графика функции не изменяется, а происходит лишь смещение вдоль оси абсцисс вправо, если он возрастает, и в

При изменении параметра а форма графика функции
не изменяется, а происходит лишь смещение вдоль
оси абсцисс вправо,
и влево, если
a = если
1 a = он
3 возрастает,
a=6
убывает.
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
33
22
11
00
11
2
3
44
55
666
777
888
999
10
10
10

29.

0.4
0.3
a = 1, = 1
0.2
0.1
3
2
1
0
1
2
3
4
5
6
7
8
9
10
0.4
0.3
a = 3, = 1
0.2
0.1
3
2
1
0
1
2
3
4
5
6
7
8
9
10
0.4
0.3
0.2
a = 6, = 1
0.1
3
2
1
0
1
2
3
4
5
6
7
8
9
10

30.

При изменении параметра изменяется форма
нормальной кривой. Если этот параметр убывает, то
кривая становится более островершинной, если
увеличивается, то кривая становится более пологой.
0.4
0.4
0.4
==
= 231
0.3
0.3
0.3
0.2
0.2
0.2
0.1
0.1
0.1
10
10
10 999 888 777 666 555 444 333 222 111
000 111
222
333
444
555
666
77
88
99 10
10

31.

0.4
0.3
= 1
0.2
0.1
10
9
8
7
6
5
4
3
2
1
0
1
2
3
4
5
6
7
8
9
10
0.4
0.3
= 2
0.2
0.1
10
9
8
7
6
5
4
3
2
1
0
1
2
3
4
5
6
7
8
9
10
0.4
0.3
= 3
0.2
0.1
10
9
8
7
6
5
4
3
2
1
0
1
2
3
4
5
6
7
8
9
10

32. Доска Гальтона

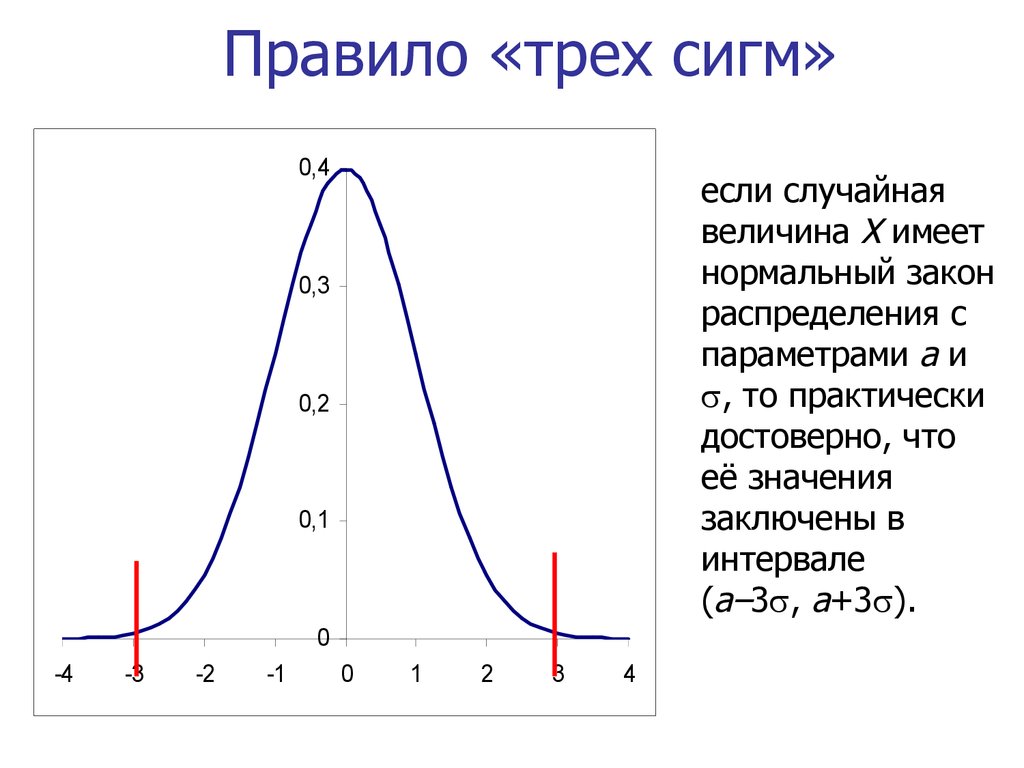
33. Правило «трех сигм»

0,4
если случайная
величина X имеет
нормальный закон
распределения с
параметрами а и
, то практически
достоверно, что
её значения
заключены в
интервале
(а–3 , а+3 ).
0,3
0,2
0,1
0
-4
-3
-2
-1
0
1
2
3
4

34.

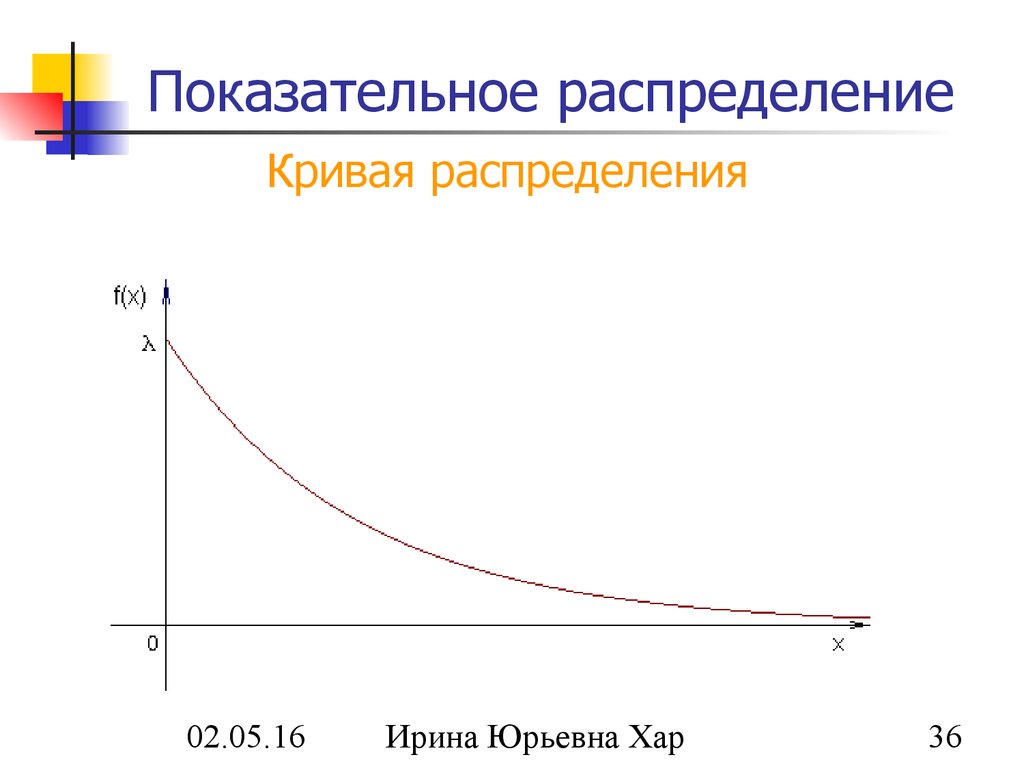
35. Показательный (экспоненциальный) закон

Непрерывная случайная величина X имеет
показательный (экспоненциальный) закон
распределения, если её плотность вероятности f(x)
имеет вид:
при x 0
0
f ( x ) x
при x 0
e

36. Показательное распределение

Кривая распределения
02.05.16
Ирина Юрьевна Хар
36

37. Показательный закон

Параметр
Математическое
ожидание
Дисперсия
Среднее квадратическое
отклонение
Вероятность попадания
СВ Х в интервал [ , ],
([ , ] [a, b])
02.05.16
1
M (X )
1
D( X ) 2
1
(X )
P ( X ) e e
Ирина Юрьевна Хар
37

38. Пример

На шоссе установлен
контрольный пункт для
проверки технического
состояния автомобилей.
Найти среднее время ожидание очередной машины
контролером Т, – если поток машин простейший и
время (в часах) между прохождениями машин через
контрольный пункт распределено по показательному
закону
5t
f (t ) 5e

39. Решение

f (t ) 5e
5t
f (t ) e
t
5
M (T ) 1 / 1 / 5(часа ) 12( минут)