Similar presentations:
Законы распределения непрерывной случайной величины. Урок № 25
1. Законы распределения непрерывной случайной величины Урок № 25
Равномерный закон распределенияПоказательное распределение
Нормальное распределение
2. Законы распределения непрерывной случайной величины
Наиболее широкое распространение длярешения теоретических и прикладных задач,
в частности в теории связи, в теории
надежности, получили следующие
теоретические законы распределения
непрерывных случайных величин:
равномерный закон;
экспоненциальный (показательный) закон;
нормальный закон.
3. Равномерный закон распределения
Непрерывная случайная величина X имеетравномерный закон распределения на отрезке
[ a; b ], если её плотность вероятности постоянна
на этом отрезке и равна нулю вне этого отрезка.
Параметры равномерного распределения
это концы отрезка [ a; b ].
4. пример равномерно распределенной непрерывной случайной величины
Шкала измерительного прибора проградуирована внекоторых единицах.
Ошибку при округлении отсчета до ближайшего
целого деления можно рассматривать как
случайную величину X, которая может принимать, с
постоянной плотностью вероятности, любое
значение между двумя соседними целыми
делениями.
Таким образом, случайная величина X имеет
равномерное распределение.
5. пример равномерно распределенной непрерывной случайной величины
Равномерному закону распределенияподчиняется разность фаз 1 2 колебаний двух
источников синусоидального напряжения
u1 A1 sin t 1 и u2 A2 sin t 2
включенных независимо.
Любое значение равновероятно в пределах 0;2
6. пример равномерно распределенной непрерывной случайной величины
При округлении чисел до n – верных знаковошибка округления распределена равномерно
на отрезке
5
1
10
5
n 1
1
10n 1
7. пример равномерно распределенной непрерывной случайной величины
В настоящее время широко распространилисьвероятностные методы приближенного решения
прикладных и математических задач на ЭВМ
(методы Монте – Карло).
Эти методы используют потоки из таблиц
случайных чисел. Каждое число такой таблицы
может рассматриваться как значение случайной
величины, распределенной по требуемому для
решения задачи закону.
8. метод Монте – Карло
Многообразие необходимых законовраспределения затрудняет построение таблиц
случайных чисел.
Таблицу случайных чисел с требуемым законом
распределения можно получить из таблицы
случайных чисел X, равномерно распределенных
на отрезке [0,1].
9. Найдем значение постоянной С равномерного распределения
Все возможные значения равномерной случайнойвеличины принадлежат интервалу [a,b]
Тогда по свойству дифференциальной функции
должно выполняться равенство
b
b
a
a
f x dx 1 C dx 1 . Тогда
C b
1
dx
a
1
b a
10. Дифференциальная функция равномерного распределения
закон равномерного распределенияаналитически можно записать так:
0 при x a ;
1
f x
при a x b ;
b a
0 при x b .
11. Записать закон распределения
Непрерывная случайная величина Xимеет равномерный закон распределения
на отрезке [ 2; 5 ]
0 при x 2;
0 при x 2;
1
1
f x
при 2 x 5; f x
при 2 x 5;
5 2
3
0 при x 5
0 при x 5
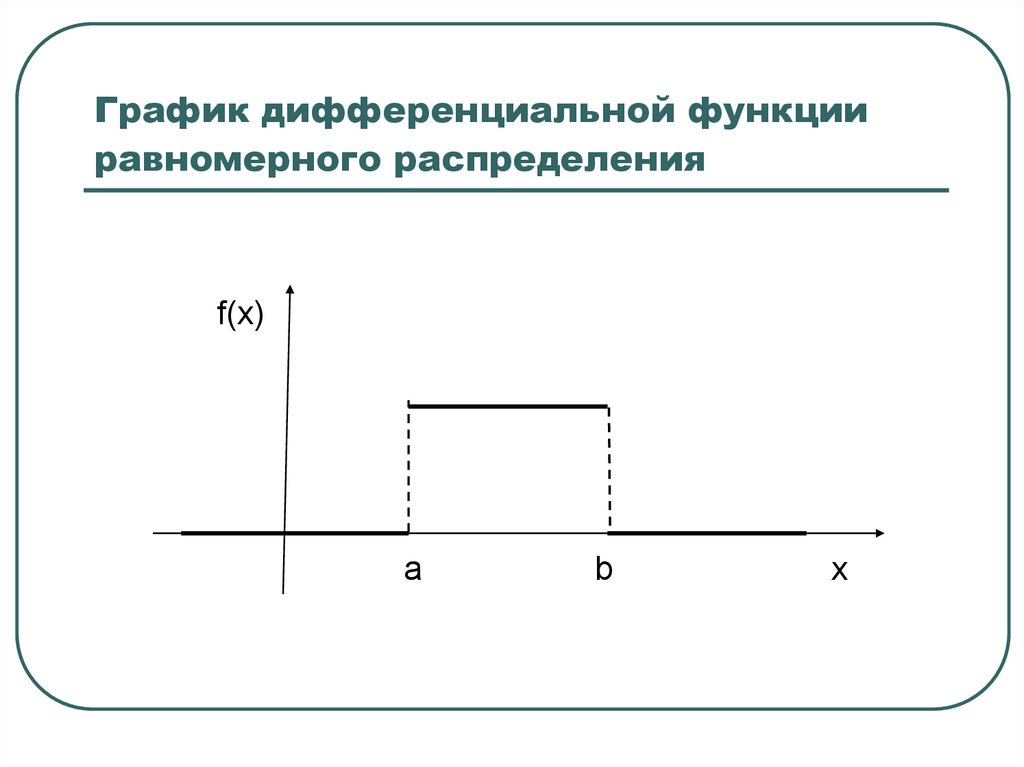
12. График дифференциальной функции равномерного распределения
f(x)a
b
x
13. Дифференциальная функция равномерного распределения
закон равномерного распределенияаналитически можно записать так:
0 при x a ;
1
f x
при a x b ;
b a
0 при x b .
14. Интегральная функция распределения
Интегральную функцию распределениянайдем по формуле
x
F x f x dx
x a
.
0 при x a ;
1
f x
при a x b ;
b a
0 при x b .
f x 0, F x 0
15. Интегральная функция распределения
Интегральная функция F x f x dxраспределения
x
a x b
a
1
f x
b a
x
0 при x a ;
1
f x
при a x b ;
b a
0 при x b .
x a
1
F x 0dx
dx
b a
a b a
x b
x
dx
b a
F x 0dx
0dx
1
b a
a b a
b
a
b
16. Интегральная функция равномерного распределения
аналитическое выражение интегральнойфункции распределения имеет вид:
0 , x a ;
x a
F x
, a x b,
b a
1 , x b ,
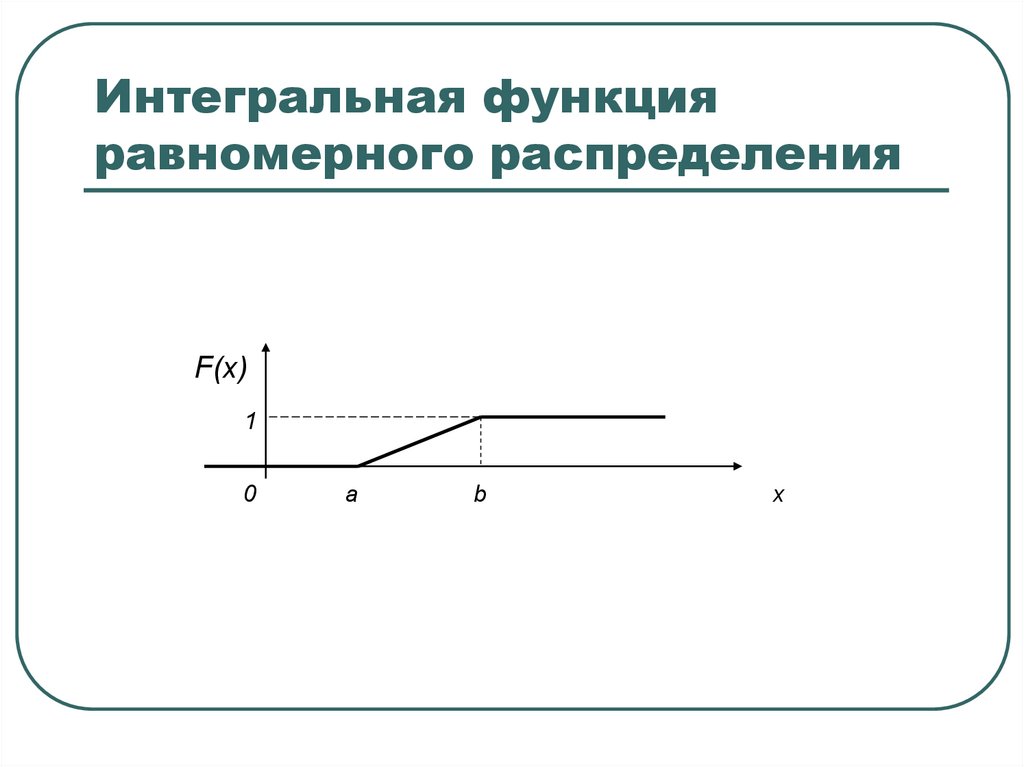
17. Интегральная функция равномерного распределения
F(x)1
0
a
b
x
18. Записать интегральную функцию распределения
Непрерывная случайная величина X имеетравномерный закон распределения на отрезке
0 , x a ;
[ 2; 5 ]
x a
F x
, a x b,
b a
1 , x b ,
0, x 2;
x 2
F x
, 2 x 5,
5 2
1, x 5,
0, x 2;
x 2
F x
, 2 x 5,
3
1, x 5,
19. Равномерный закон распределения
Если случайная величина подчиняетсяравномерному закону распределения, то она
с одинаковой вероятностью может принимать
значения внутри любых равновеликих
интервалов, расположенных в области
возможных значений случайной величины.
Поэтому закон равномерного распределения
называют законом равной вероятности.
20. Числовые характеристики равномерного распределения
Равномерная случайная величина неимеет максимума, а значит и моды.
Математическое ожидание равномерной
случайной величины равно
a b
M (X )
и равно медиане.
2
Дисперсия равна
2
b a
D( X )
12
21. Задача
Поезда метрополитена идут регулярно синтервалом 2 минуты. Пассажир выходит на
платформу в случайный момент времени.
Какова вероятность того, что ждать пассажиру
придется не более полминуты?
Найти математическое ожидание и среднее
квадратическое отклонение случайной величины
X – времени ожидания поезда.
22. Решение
Случайная величина X – время ожидания поезда,является непрерывной случайной величиной с
равномерным распределением на отрезке от 0 до 2.
Параметры распределения: а = 0, b = 2.
Функция распределения равна f(x) = 1/(b – a) = ½ на
отрезке [0,2] и нулю вне этого отрезка.
Интегральная функция распределения равна
0, x 0;
x 0
F x
, 0 x 2,
2
0
1, x 2,
0, x 0;
x
F x , 0 x 2,
2
1, x 2,
23. Решение
Вероятность того, что ждать пассажиру придется неболее полминуты найдем по формуле
F(b) – F(a) = F(0,5) – F(0) = 0,5/2 – 0/2 = 0,25
0, x 0;
x
F x , 0 x 2,
2
1, x 2,
24. Решение
Математическое ожидание равномернойслучайной величины равно M ( X ) a b
2
M(X) = (0 + 2)/2 = 1
В среднем ждать поезда придется 1 минуту.
Дисперсия равномерной случайной величины
равна
2
b a
D( X )
12
D(X) = (2 – 0)2 /12 = 1/3, ( X ) D( X ) 1/ 3 0,58 мин.
25. Экспоненциальный (показательный) закон распределения
При решении прикладных задач физики,биологии, астрономии, радиотехники,
теории информации, теории надежности и
т.д. приходится сталкиваться с обширным
классом случайных величин,
распределение которых достаточно
хорошо описывается экспоненциальным
(показательным) законом.
26. Экспоненциальный (показательный) закон распределения
Непрерывная случайная величина X имеетпоказательный закон распределения с
параметром , если её плотность вероятности
имеет вид
x
e
( x)
0
при x 0
при x 0
где положительная константа
Показательное распределение имеет один
параметр
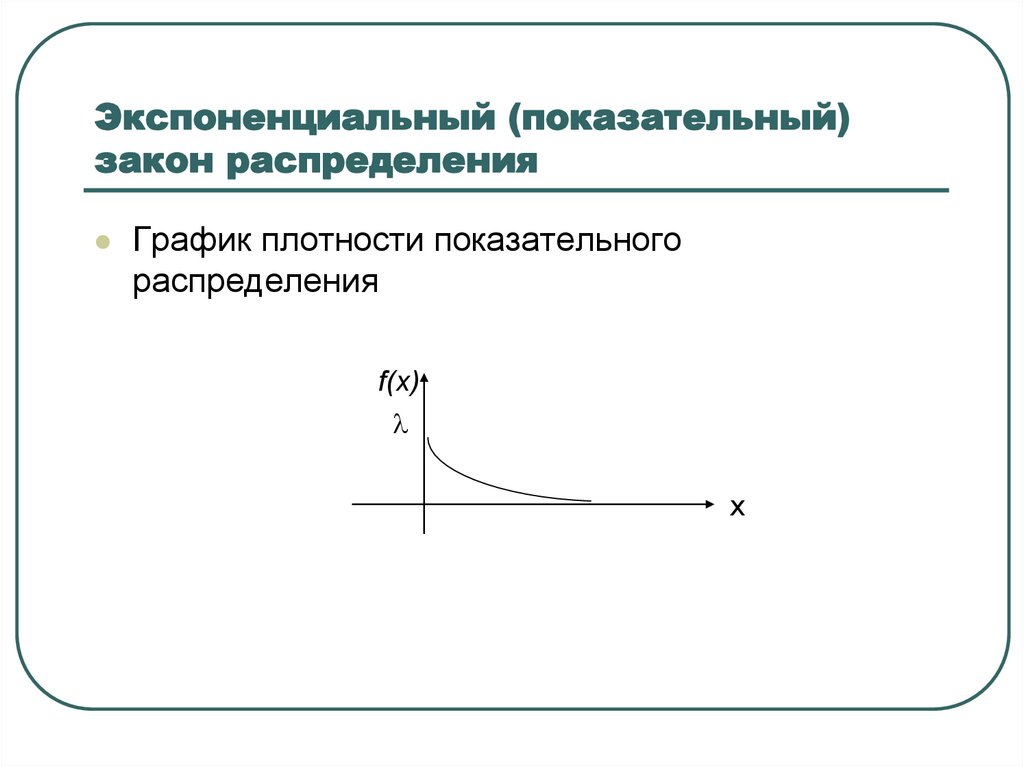
27. Экспоненциальный (показательный) закон распределения
График плотности показательногораспределения
f(x)
x
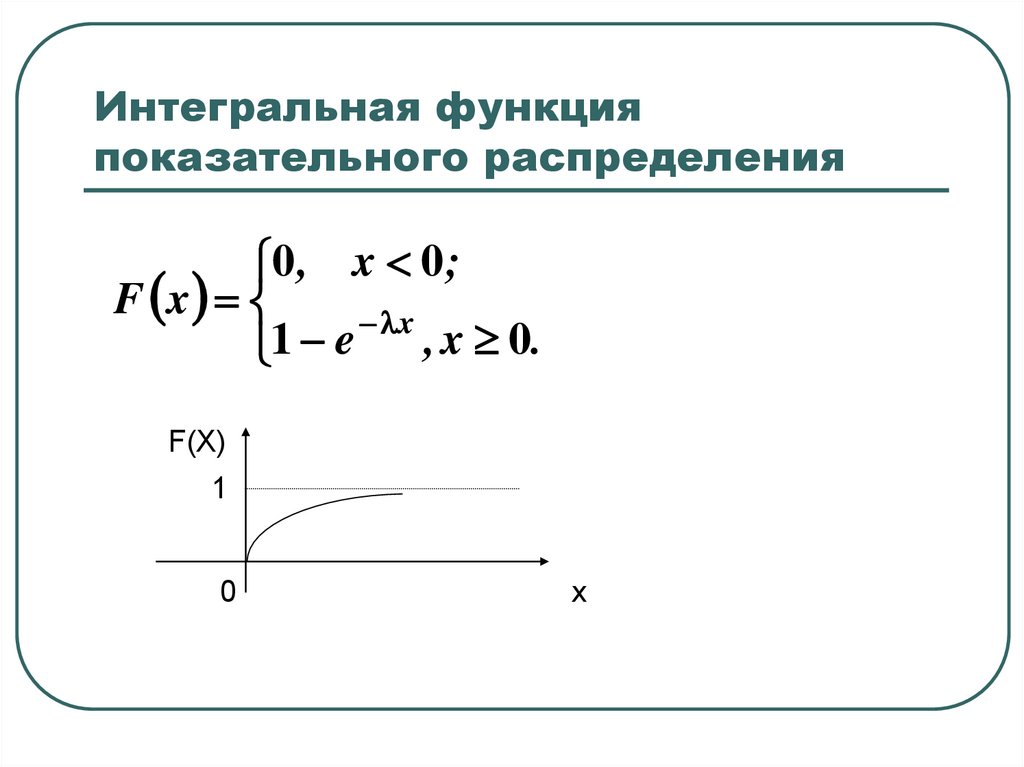
28. Интегральная функция показательного распределения
0 , x 0 ;F x
x
, x 0.
1 e
F(X)
1
0
x
29. Числовые характеристики показательного распределения
Математическое ожидание случайной величины,распределенной по показательному закону равно
M(X) = 1/λ.
Дисперсия равна D(X) = 1/λ2
Математическое ожидание и среднее
квадратическое отклонение, в случае
экспоненциального закона, равны между собой.
30. Примеры показательного распределения
Примеры случайных величин, для описанияраспределения которых применяется показательный
закон:
длительность телефонного разговора;
продолжительность жизни атома радиоактивного
вещества;
срок безотказной работы прибора;
время уничтожения цели одиночными выстрелами;
время обслуживания заявки в системе массового
обслуживания.
31. Функция надежности. Показательный закон надежности
Показательное распределение широкоприменяется в приложениях, в частности, в
теории надежности, одним из основных понятий
которой является функция надежности.
Под элементом будем подразумевать некоторое
устройство, независимо от того, «простое» оно
или «сложное».
Пусть элемент начинает работать в момент
времени t0, а по истечении времени
длительностью t происходит отказ.
32. Функция надежности
Обозначим через T – непрерывную случайнуювеличину – длительность безотказной работы
элемента.
Если элемент проработал безотказно время,
меньшее чем t, то следовательно, за временем
длительностью t наступает отказ.
33. Функция надежности
Таким образом, интегральная функция F t P T tопределяет вероятность отказа за время
длительностью t.
Так как события T t и T t противоположны,
то вероятность безотказной работы за то же
время равна
P T t 1 P T t P T t 1 F t
34. Определение
Функцией надежности R(t) называют функцию,определяющую вероятность безотказной
работы элемента за время длительностью t:
R(t) = P(T > t)
Часто длительность безотказной работы
элемента имеет показательное распределение,
функция распределения которого F(t) = 1 – e – λ t
Показательным законом надежности называют
функцию надежности, определяемую
равенством: R(t) = e – λ t,
где λ – интенсивность отказов.
35. Характеристическое свойство показательного закона надежности
Вероятность безотказной работы элементана интервале времени длительностью t не
зависит от времени предшествующей работы
до начала рассматриваемого интервала, а
зависит только от длительности времени t
(при заданной интенсивности отказов λ).
Если случайная величина обладает этим
свойством, то она распределена по
показательному закону.
36. Нормальный закон распределения
ОпределениеНормальным называется распределение
вероятностей непрерывной случайной величины,
которое описывается плотностью вероятности
f ( x)
1
x 2
e
( x mx ) 2
2 2x
;
Нормальный закон распределения также
называется законом Гаусса.
37.
Нормальный закон распределения занимаетцентральное место в теории вероятностей. Это
обусловлено тем, что этот закон проявляется во
всех случаях, когда случайная величина является
результатом
действия
большого
числа
различных факторов.
К
нормальному закону приближаются все
остальные законы распределения.
38. Функция распределения нормального закона
Найдем функцию распределения F(x).F ( x)
1
x
e
x 2
( x mx ) 2
2 2x
dx
39. Кривая Гаусса
График плотности нормального распределенияназывается нормальной кривой или кривой
Гаусса.
Нормальная кривая обладает следующими
свойствами:
1) Функция определена на всей числовой оси.
2) При всех х функция распределения принимает
только положительные значения.
40. Свойства нормальной кривой
3) Ось ОХ является горизонтальной асимптотойграфика плотности вероятности, т.к. при
неограниченном возрастании по абсолютной
величине аргумента х, значение функции
стремится к нулю.
4) Найдем экстремум функции.
y
x m
3
2
e
( x m)2
2 2
0;
x m;
41. Вопросы к теме
1. Дайте определения непрерывнойслучайной величины имеющей
равномерное распределение.
2. Привести примеры равномерно
распределенных величин.
42. Вопросы к теме
3. Записать функцию F(x) дляравномерного распределения.
4. Записать формулы для вычисления
математического ожидания и
дисперсии равномерно
распределенной величины.
43. Вопросы к теме
5. Записать параметры равномерногораспределения и объяснить их смысл.
6. Как найти вероятность попадания
равномерной случайной величины в
заданный интервал?
44. Вопросы к теме
7. Дайте определения непрерывнойслучайной величины имеющей
показательное распределение.
8. Записать функцию F(x) для
показательного распределения.
45. Вопросы к теме
9. Записать числовые характеристикипоказательного распределения.
10. Описать функцию надежности и ее
свойство.
46. Домашнее задание
Калинина В. Н.Глава 6. Виды распределений.
§ 6.1 Равномерное распределение,
§ 6.6 Показательное распределение.










































 mathematics
mathematics








