Законы распределения случайных величин

1. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН

Распределение изучаемого признака в выборке называется эмпирическим или
выборочным, а во всей генеральной совокупности - теоретическим.
Для изучения эмпирического распределения используется вариационный ряд,
а для изучения теоретического распределения - закон (функция) распределения.
Одна из задач вариационного анализа - установление вида функции (закона)
теоретического
распределения,
которому
соответствует
эмпирическое
распределение выборочной совокупности.
Законом или функцией распределения случайной величины называется
соотношение, устанавливающее связь между значениями случайной величины и
соответствующими им вероятностями.
Закон распределения является наиболее полной и исчерпывающей
характеристикой генеральной совокупности, также как вариационный ряд для
выборочной совокупности.
Закон распределения, как и вариационный ряд, может быть задан в трех формах:
табличной,
графической
аналитической

2.

-
-
+
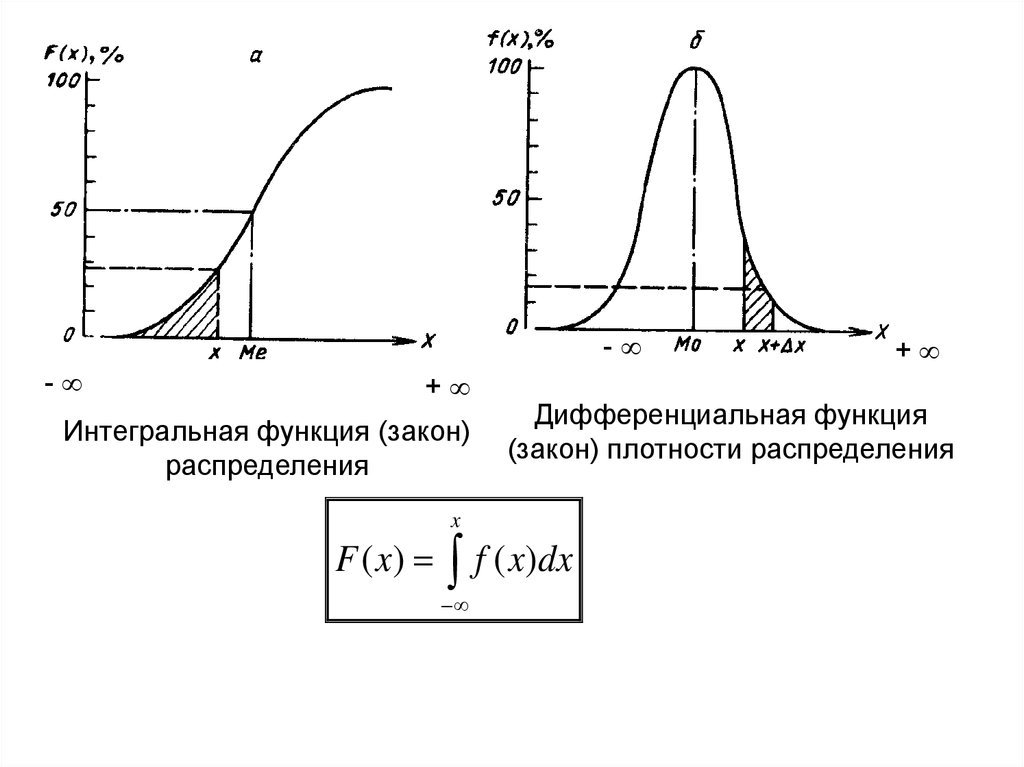
Интегральная функция (закон)
распределения
x
F ( x)
Дифференциальная функция
(закон) плотности распределения
f ( x)dx
+

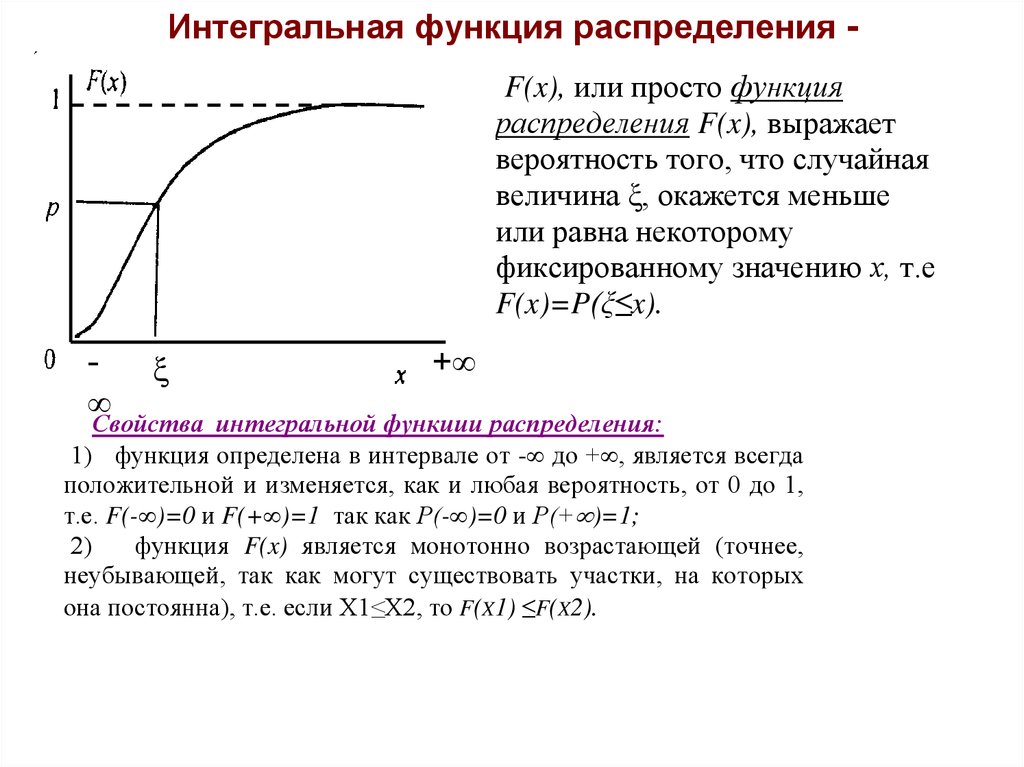
3. Интегральная функция распределения -

Интегральная функция распределения F(x), или просто функция
распределения F(x), выражает
вероятность того, что случайная
величина ξ, окажется меньше
или равна некоторому
фиксированному значению х, т.е.
F(x)=P(ξ≤x).
+
Свойства интегральной функиии распределения:
1) функция определена в интервале от - до + , является всегда
положительной и изменяется, как и любая вероятность, от 0 до 1,
т.е. F(- )=0 и F(+ )=1 так как Р(- )=0 и Р(+ )=1;
2)
функция F(x) является монотонно возрастающей (точнее,
неубывающей, так как могут существовать участки, на которых
она постоянна), т.е. если Х1≤Х2, то F(X1) ≤F(X2).

4.

Интегральная функция
распределения
Накопленные частости
Кумулятивная кривая содержаний меди
1,2
для непрерывных величин
1
0,8
0,6
0,4
0,2
0
0,53
0,65
Ме
0,77
0,89
1,01
1,13
1,25
1,37
Середины классов содержаний меди, %
Ряд1
Ряд2
-
+
x
F ( x)
f ( x)dx
Накопленные частоты
Интегральная гистограмма вариационного ряда
содержаний меди (вариант 1)
60
50
40
30
20
10
0
44
47
49
50
0,951,07
1,071,19
1,191,31
1,311,43
33
21
3
0,470,59
10
0,590,71
0,710,83
0,830,95
Интервалы группирования содержаний меди, %

5.

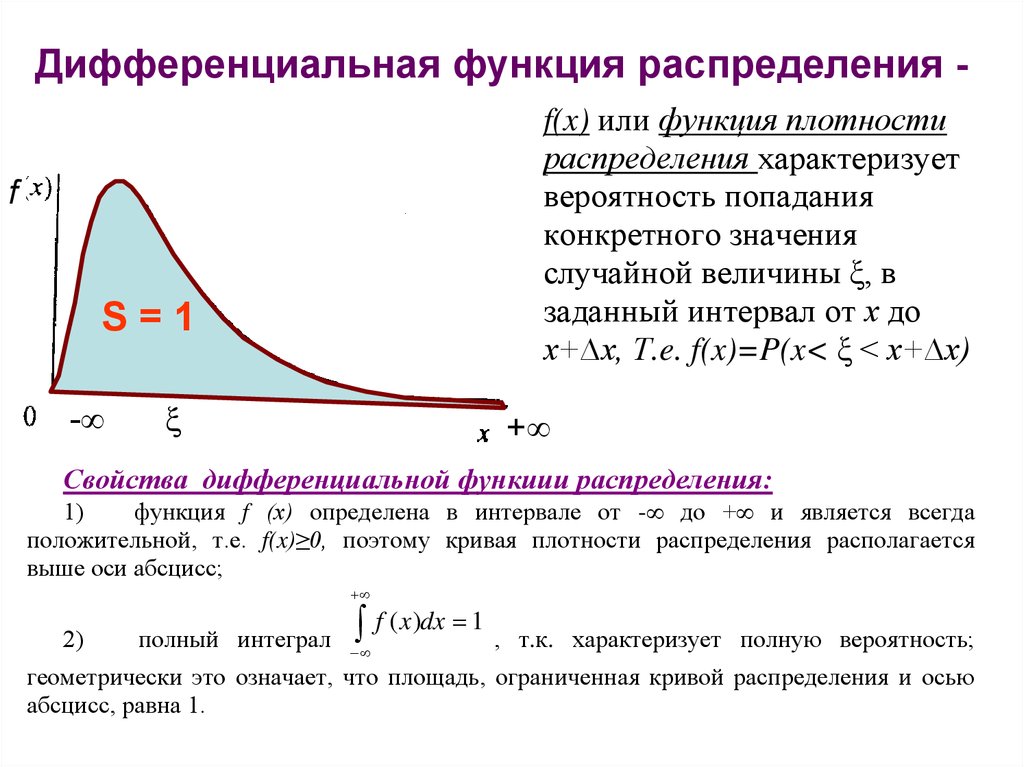
Дифференциальная функция распределения f(x) или функция плотности
распределения характеризует
вероятность попадания
конкретного значения
случайной величины ξ, в
заданный интервал от х до
х+∆х, Т.e. f(x)=P(x< ξ < х+∆х)
f
S=1
-
+
Свойства дифференциальной функиии распределения:
1)
функция f (х) определена в интервале от - до + и является всегда
положительной, т.е. f(x)≥0, поэтому кривая плотности распределения располагается
выше оси абсцисс;
2)
полный интеграл
f ( x)dx 1 ,
т.к. характеризует полную вероятность;
геометрически это означает, что площадь, ограниченная кривой распределения и осью
абсцисс, равна 1.

6.

Эмпирические частоты, ед.
Дифференциальная функция
плотности распределения
14
12
10
8
6
4
2
0
0,53
Полигон распределения содержаний меди
0,65
0,77
0,89
1,01
1,13
1,25
1,37
Середины классов группирования содержаний меди, %
Гистограмма вариационного ряда содержаний меди
(вариант 1)
+
Частоты
-
14
12
10
8
6
4
2
0
11
12
11
7
3
0,470,59
3
0,590,71
0,710,83
0,830,95
0,951,07
1,071,19
2
1,191,31
Интервалы группирования содержаний меди, %
1
1,311,43

7.

Дифференциальная
функция
является
первой
производной от интегральной функции. Обе функции
связаны соотношениями:
x
dF ( x)
f ( x) F ( x)
dx
.
и
F ( x)
f ( x)dx

8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ТЕОРЕТИЧЕСКИХ РАСПРЕДЕЛЕНИЙ

Меры положения и меры рассеяния.
Матем. ожиданием называется сумма произведений значений
случайной величины на соответствующие им вероятности или
плотности вероятности. В отличие от среднего рассчитывается не
через частоты, а через вероятности по формулам:
n
M x xi p i
i 1
и
Mx
x f ( x)dx
где хi, - значения случайной величины, pi, - соответствующие им
вероятности, f(x) - плотность вероятности. Обозначается MX, M[X], a,
μ, тх или МОЖ
Математическое ожидание по своему смыслу эквивалентно
среднему значению вариационного ряда. Оно характеризует центр
теоретического распределения, около которого группируется
подавляющее количество значений случайной величины.

9.

Дисперсия характеризует степень рассеяния отдельных значений
или интервалов значений случайной величины относительно ее
математического ожидания Мх. Обозначается Dx, D[X], 2х и
рассчитывается по формулам соответственно для дискретной и
непрерывной величины:
n
х2 ( xi Mx ) 2 pi
i 1
и
х2 ( x Mx ) 2 f ( x)dx
Квадратный корень из дисперсии называется средним
квадратическим
отклонением
x, a среднекаадратическое
отклонение, нормированное на математическое ожидание, коэффициентом вариации V :
х
2
х
и
V
х
Мх
100%

10.

Показатели асимметрии и эксцесса:
n
А
3
(
х
Mx
)
pi
i
i 1
x3
E
i 1
;
x3
n
(х
A
3
(
x
Mx
)
f ( x)dx
Mx ) pi
4
i
x4
E
;
;
4
(
x
Mx
)
f ( x)dx
x4

11. ТЕОРЕТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ В ГЕОЛОГИИ

для непрерывных величин:
нормальный, логнормальный
для дискретных величин:
биномиальный, закон Пуассона

12. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Нормальным
называется
распределение
случайной
величины, интегральная F(x) и дифференциальная f(x) функции
которого имеют вид:
1
F ( x)
2
x
е
( х Мх ) 2
2 2
dx
1
f ( x)
e
2
( x Mx) 2
2 2
где Мх и 2 - параметры распределения (математическое
ожидание и дисперсия).
Обозначается N (X, Мх, х),
N означает принадлежность случайной величины X к
нормальному распределению с параметрами Мх и х.

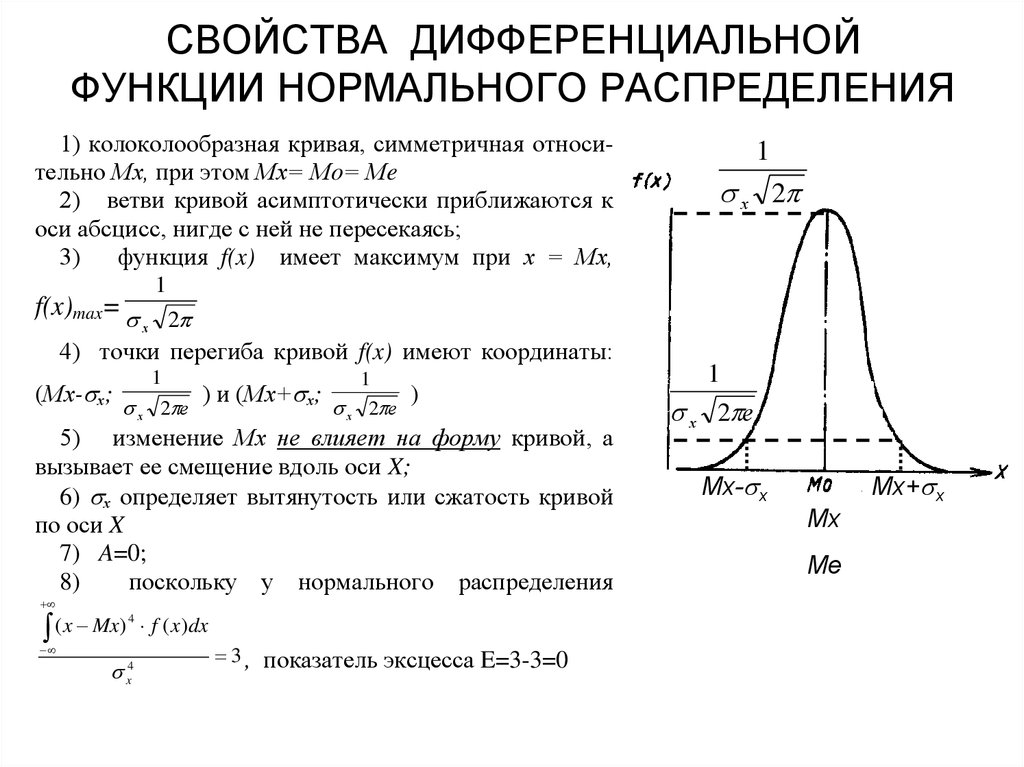
13. СВОЙСТВА ДИФФЕРЕНЦИАЛЬНОЙ ФУНКЦИИ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ

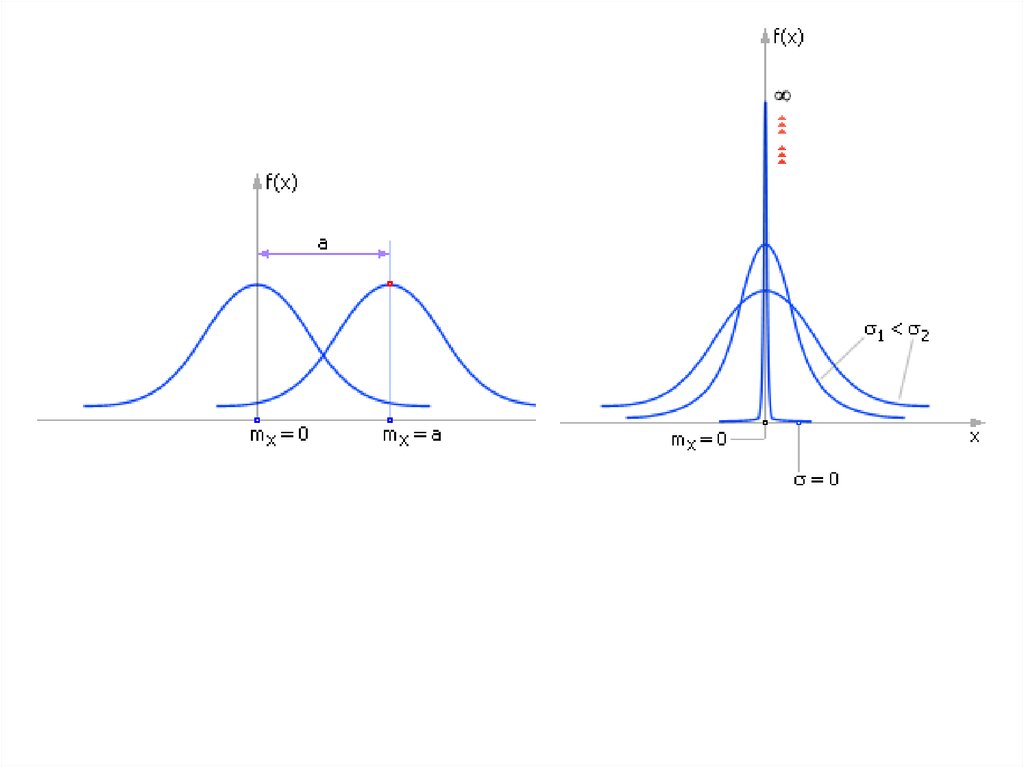
1) колоколообразная кривая, симметричная относительно Мх, при этом Мх= Мo= Мe
2) ветви кривой асимптотически приближаются к
оси абсцисс, нигде с ней не пересекаясь;
3)
функция f(x) имеет максимум при х = Мх,
f(x)max=
2
х
1
х 2 е
) и (Мх+ х;
1
х 2 е
)
5) изменение Мх не влияет на форму кривой, а
вызывает ее смещение вдоль оси X;
6) х определяет вытянутость или сжатость кривой
по оси X
7) A=0;
8)
поскольку у нормального распределения
( x Mx)
4
x4
х 2
1
4) точки перегиба кривой f(x) имеют координаты:
(Мх- х;
1
f ( x)dx
3 , показатель эксцесса E=3-3=0
1
х 2 е
Мх- х
Мх
Ме
Мх+ х

14.

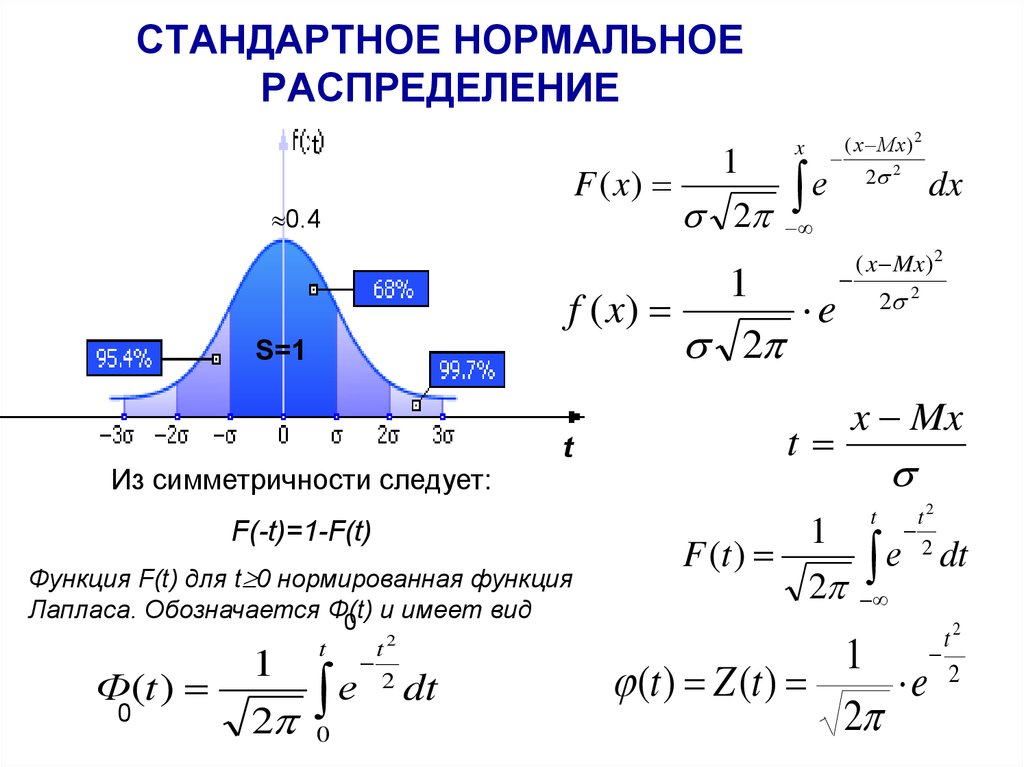
15. СТАНДАРТНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

t
F ( x)
0.4
f ( x)
S=1
t
Из симметричности следует:
F(-t)=1-F(t)
Функция F(t) для t 0 нормированная функция
Лапласа. Обозначается Ф(t)
0 и имеет вид
Ф(t )
0
1
2
t
е
0
2
t
2
dt
1
2
1
2
x
е
( х Мх ) 2
2 2
dx
e
t
1
F (t )
2
( x Mx ) 2
2 2
x Mx
t
е
t2
2
dt
1
(t ) Z (t )
e
2
t2
2

16.

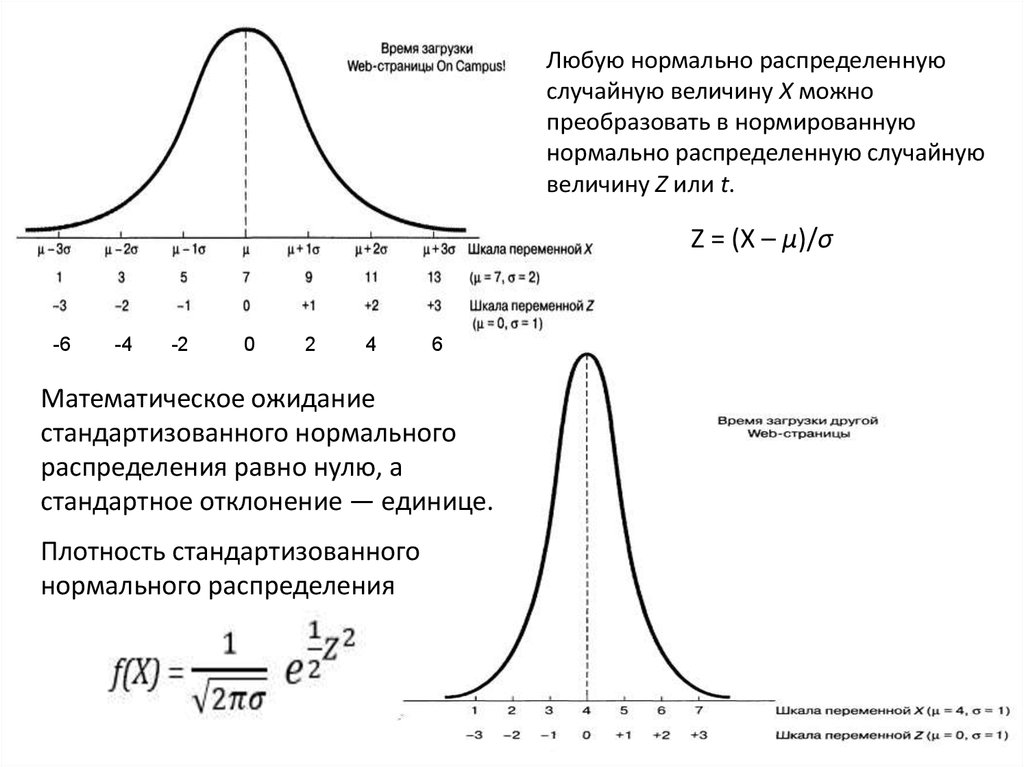
Любую нормально распределенную
случайную величину X можно
преобразовать в нормированную
нормально распределенную случайную
величину Z или t.
Z = (Х – μ)/σ
-6
-4
-2
0
2
4
6
Математическое ожидание
стандартизованного нормального
распределения равно нулю, а
стандартное отклонение — единице.
Плотность стандартизованного
нормального распределения

17. ЛОГНОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Логарифмически нормальное (логнормальное) распределение,
при котором нормально распределены логарифмы значений случайной
величины.
Интегральная и дифференциальная функции логнормального
распределения:
F (ln x)
ln x
1
ln x 2
f (ln x)
е
(ln х М ln х ) 2
2
2 ln
x
d ln x
1
ln x 2
e
(ln x M ln x ) 2
2 ln x 2
имеет положительные коэффициенты асимметрии и эксцесса, т.е.
является правоасимметричным (А>0) и крутовершинным (Е>0).
Мо<Ме<Мх. Определяются из соотношений
Mx e
M ln x 0.5 ln2 x
Me e
M ln x
Mo e
M ln x ln2 x

18.

19. ПРОВЕРКА ГИПОТЕЗЫ О ЗАКОНЕ РАСПРЕДЕЛЕНИЯ

Графический
Экспрессный метод графической проверки
Аналитический:
1) 2 -критерий Пирсона (хи-квадрат)
2) критерий Колмогорова (критерий )
Сравнение эмпирических частот пэj по классам
группирования с теоретическими частотами пTj, при этом
параметры нормального распределения Мх и
приравниваются к их выборочными оценками U и S.
Отличие:
в случае критерия Пирсона сравниваются
дифференциальные кривые эмпирического и теоретического
распределения (т.е. частотные ряды распределения),
в случае критерия Колмогорова - интегральные кривые (т.е.
ряды накопленных частот).

20. Критерий Пирсона 2

Критерий Пирсона 2
2
(
n
n
)
iT
2 iЭ
niT
i 1
k
niэ и niТ - эмпирические и теоретические частоты для проверяемого
закона распределения выборочных данных, сгруппированных в k интервалов.
Графически это суммарная площадь
теоретическим полигонами распределения.
Теоретические частоты рассчитываются:
niT
где
между
эмпирическим
2
ˆ
(
X
X
)
X
N
j
2
X N f j ( Xˆ j , X , S x )
exp
2
2S x
S x 2
f j ( Xˆ j , X , S x2 )
- значения функции плотности нормального
ˆ
распределения для середины j-го интервала X
среднем
U
и дисперсии Sx.
j
при заданном выборочном
и

21.

Эмпирические
частоты, ед.
Полигон распределения содержаний
меди
14
12
10
8
6
4
2
0
0.53
0.65
0.77
0.89
1.01
1.13
1.25
1.37
Середины классов группирования содержаний
меди, %
Обычно 2 применяется, когда N>60

22.

Если
2
р
Т2
<
, то с вероятностью p=1-
принимается нулевая гипотеза, т.е. гипотеза о
том,
что
эмпирическое
распределение
не
противоречит нормальному.
Если
>
, то нулевая гипотеза
отклоняется и принимается альтернативная гипотеза
о том, что эмпирическое распределение не
соответствует нормальному.
р2
2
Т

23. Критерий Колмогорова 

Критерий Колмогорова
Численно критерий равен максимальному отклонению
эмпирических накопленных частот от теоретических и рассчитывается по
формуле:
Dmax
N
n sэ n sT
N
,
где Dmax - максимальное значение абсолютной разности между
эмпирическими накопленными частотами (nsэ) и теоретическими (nsТ).
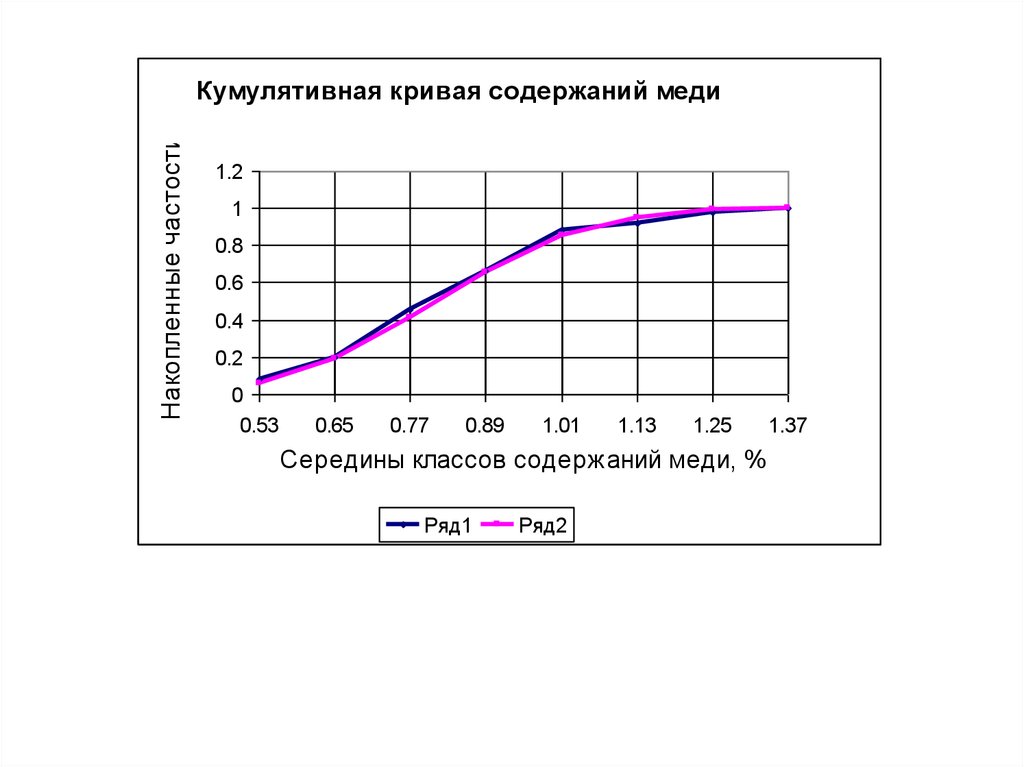
Графически критерий соответствует максимальному расстоянию
между эмпирической и теоретической кумулятивными кривыми.
сравнивают значение р с Т для принятого уровня значимости α.
Теоретическое значение Т не зависит от N и числа степеней свободы, а
определяется только уровнем значимости:
, Т = 1,36, при =0,01 Т =1,63.
р< Т, то с вероятностью р=1- нулевая гипотеза
при =0,05
Если
о том, что
эмпирическое распределение не противоречит нормальному, принимается.

24.

Накопленные частости
Кумулятивная кривая содержаний меди
1.2
1
0.8
0.6
0.4
0.2
0
0.53
0.65
0.77
0.89
1.01
1.13
1.25
Середины классов содержаний меди, %
Ряд1
Ряд2
1.37