Геометричні перетворення графіків функцій

1. Геометричні перетворення графіків функцій

2. Паралельне перенесення вздовж осі ординат

y f ( x)
x0 , y 0
y f ( x) b
x0 , y 0 b
Графік функції y = f(x)+b можна отримати в
результаті паралельного перенесення
графіка функції y = f(x) на b одиниць угору,
якщо b>0, і на -b одиниць вниз, якщо b<0

3. Паралельне перенесення вздовж осі абсцис

y f ( x)
x0 , y 0
y f (x a)
x0 a , y 0
Графік функції y = f(x+а) можна отримати в
результаті паралельного перенесення
графіка функції y = f(x) на а одиниць вліво,
якщо а>0, і на -а одиниць вправо, якщо а<0

4.

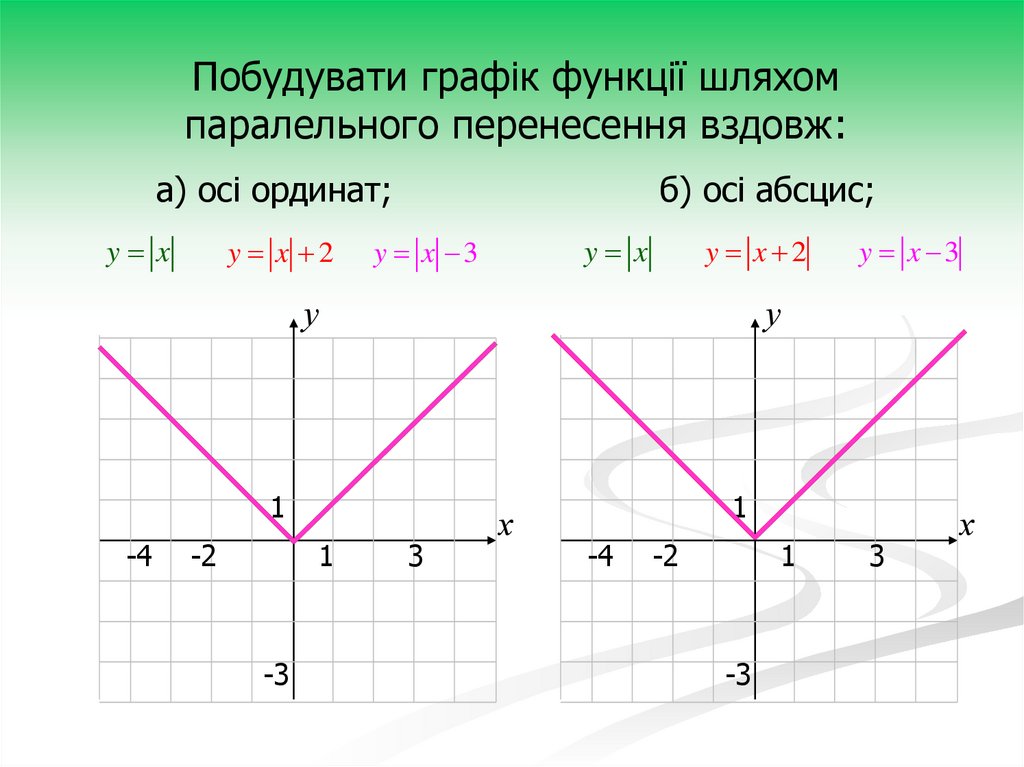
Побудувати графік функції шляхом
паралельного перенесення вздовж:
а) осі ординат;
y x
y x 2
б) осі абсцис;
y x
y x 3
y x 2
у
у
1
-4
-2
1
-3
y x 3
3
х
1
-4
-2
1
-3
3
х

5. Паралельне перенесення вздовж осі ординат

y f ( x)
y f ( x) b
y b f (x )
Графік функції y = f(x)+b можна отримати в
результаті паралельного перенесення осі
абсцис на b одиниць вниз, якщо b>0, і на -b
одиниць угору, якщо b<0

6.

Побудова графіка функції шляхом паралельного
перенесення осі абсцис
y x
у
y x 2
y 2 x
1
0
1
х

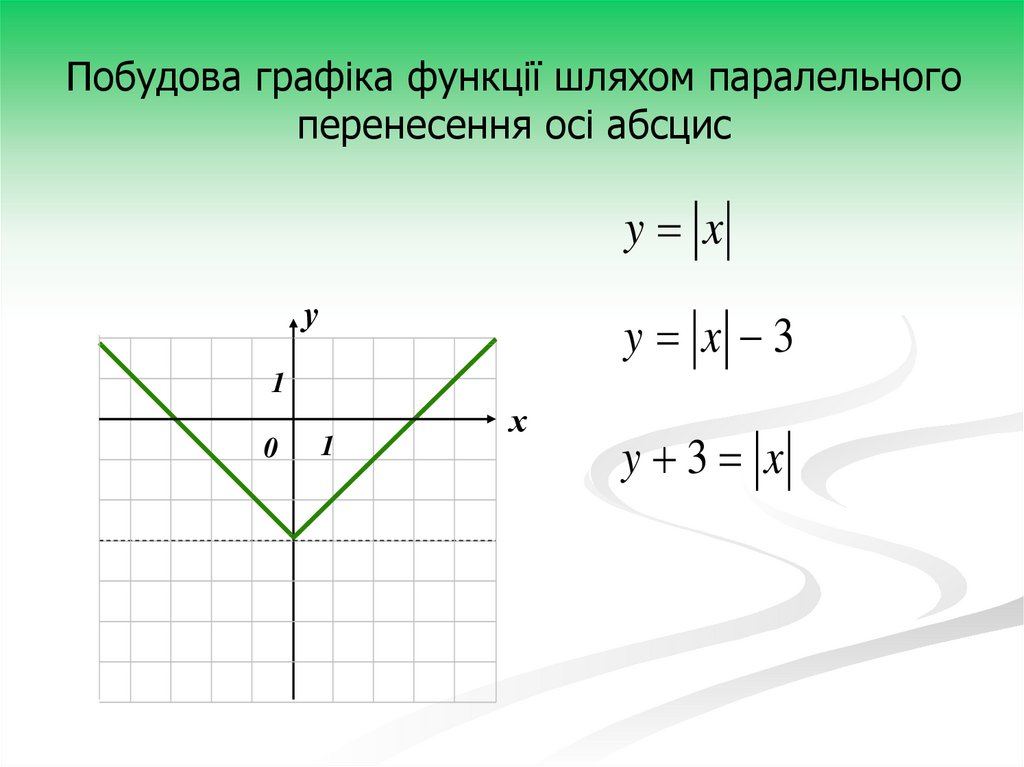
7.

Побудова графіка функції шляхом паралельного
перенесення осі абсцис
y x
у
y x 3
1
0
1
х
y 3 x

8. Паралельне перенесення вздовж осі абсцис

y f ( x)
y f (x a)
Графік функції y = f(x+а) можна отримати
в результаті паралельного перенесення осі
ординат на а одиниць вправо, якщо а>0, і на
-а одиниць вліво, якщо а<0

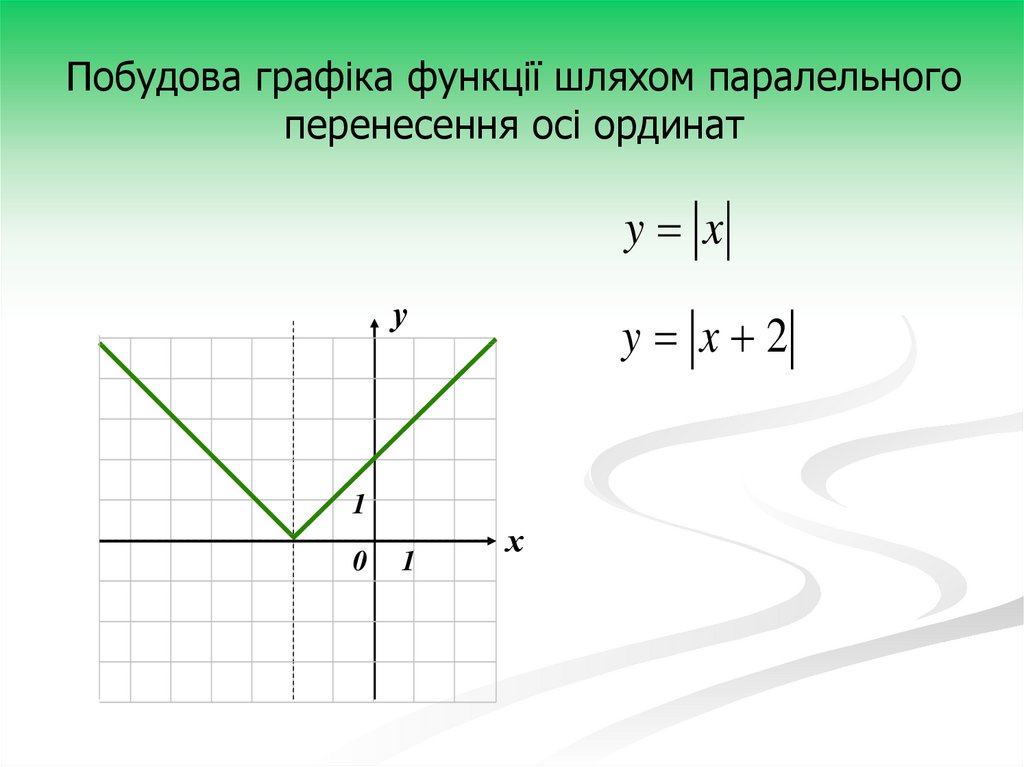
9.

Побудова графіка функції шляхом паралельного
перенесення осі ординат
y x
у
y x 2
1
0
1
х

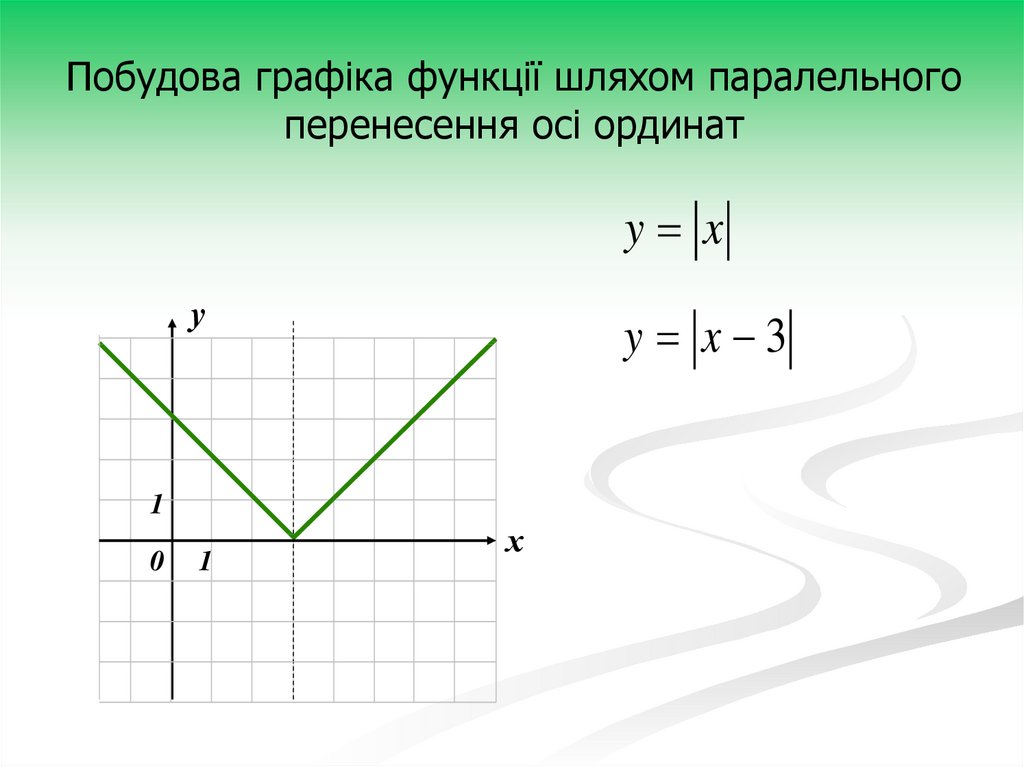
10.

Побудова графіка функції шляхом паралельного
перенесення осі ординат
y x
у
y x 3
1
0
1
х

11.

Побудова графіка функції шляхом паралельного
перенесення осей координат
y x
у
0
1
y x 3 2
х

12. Розтяг (стиск) графіка в k разів від осі абсцис

y f ( x)
y m f ( x ), m 0
x0 , y 0
x0 , m y 0
Графік функції у = т f(x) можна отримати
з графіка функції y = f(x) у результаті
розтягу в т разів від осі абсцис, якщо т>1,
або в результаті
стиску в 1 разів до осі абсцис, якщо 0<т<1
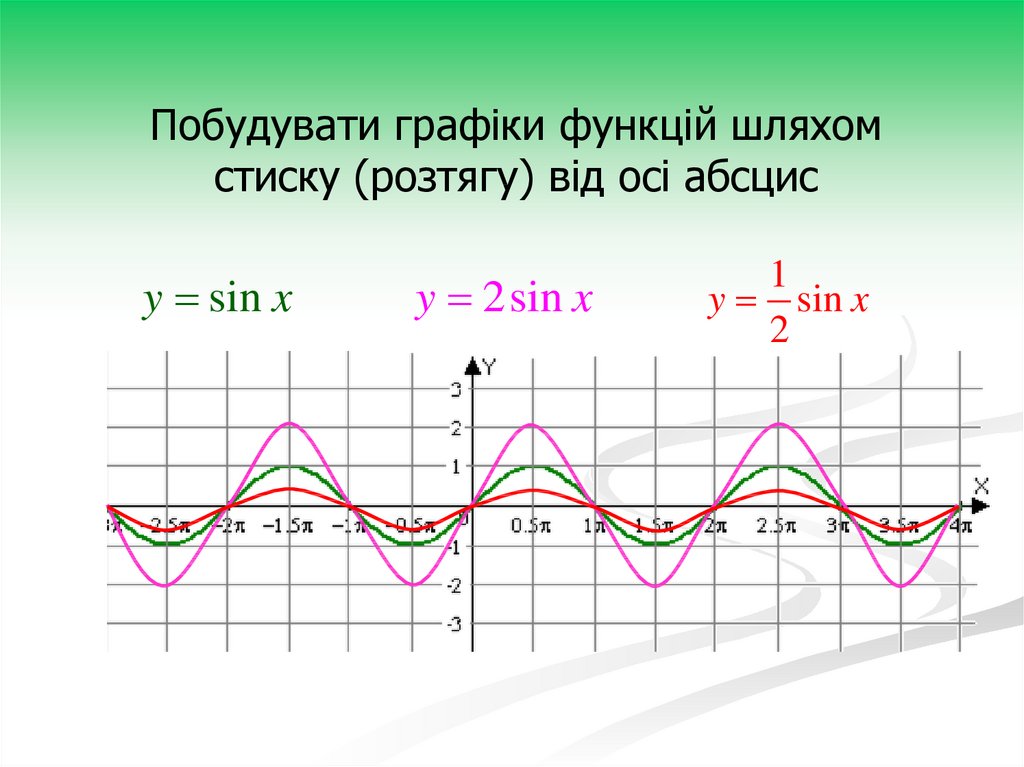
т

13.

Побудувати графіки функцій шляхом
стиску (розтягу) від осі абсцис
y sin x
y 2sin x
1
y sin x
2

14. Розтяг (стиск) графіка в k разів від осі ординат

y f ( x)
x0 , y 0
y f ( k x ), k 0
x0
, y0
k
Графік функції y = f(kx) можна отримати з
графіка функції y = f(x) у результаті
стиску в k разів до осі ординат, якщо k>1,
або в результаті
1
розтягу в
разів від осі ординат, якщо
k
0<k<1

15.

Побудувати графіки функцій шляхом
стиску (розтягу) від осі ординат
y x
у
1
-4
-2
1
-3
y x
y 2x
3
х
1
y x
2
у
1
-4
-2
1
-3
3
х

16. Симетрія графіка функції відносно осі абсцис

y f ( x)
y f ( x)
x0 , y 0
x0 , y 0
Графік функції y = - f(x) можна отримати з
графіка функції y = f(x) у результаті
симетрії відносно осі абсцис

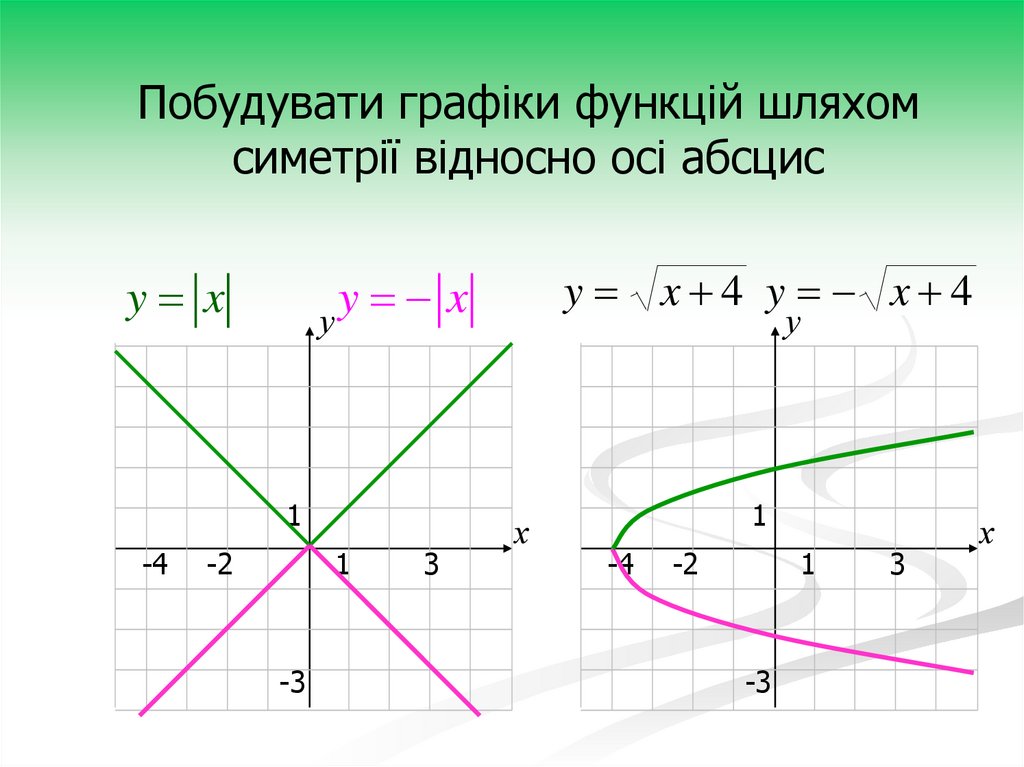
17.

Побудувати графіки функцій шляхом
симетрії відносно осі абсцис
y x
1
-4
y x 4 y x 4
y
x
у
-2
1
-3
3
у
х
1
-4
-2
1
-3
3
х

18. Симетрія графіка функції відносно осі ординат

y f ( x)
x0 , y 0
y f ( x)
x 0 , y 0
Графік функції у = f(-x) можна отримати з
графіка функції y = f(x) у результаті
симетрії відносно осі oрдинат

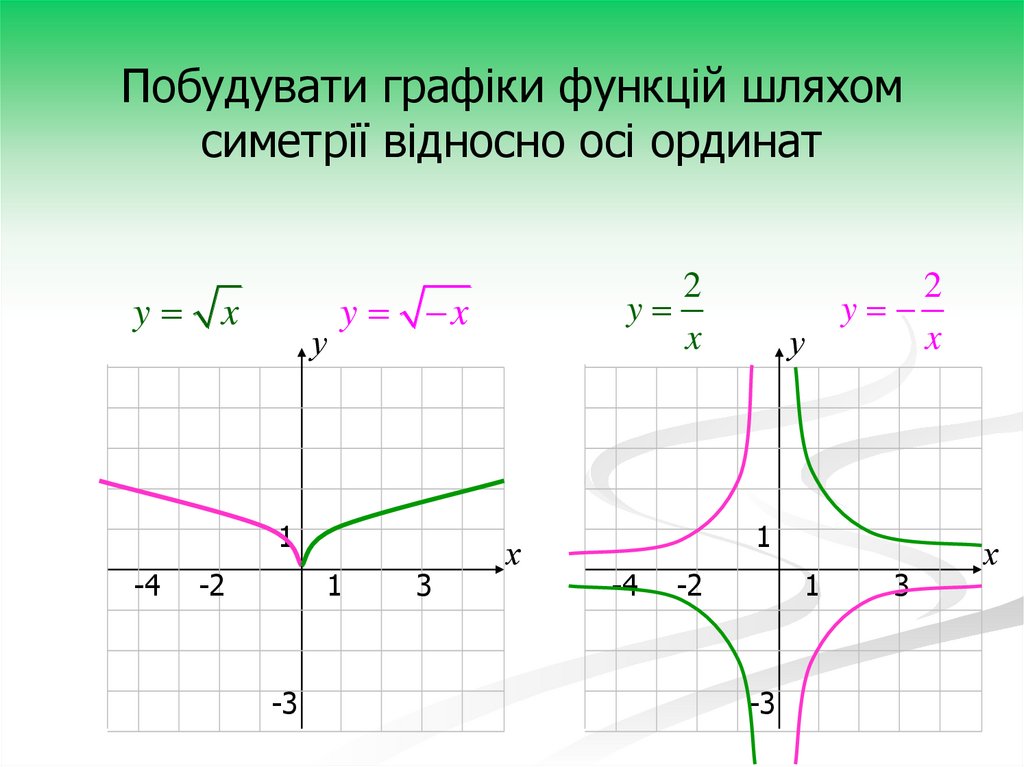
19.

Побудувати графіки функцій шляхом
симетрії відносно осі ординат
y x
у
y x
1
-4
-2
1
-3
2
y
x
3
х
2
y
x
у
1
-4
-2
1
-3
3
х

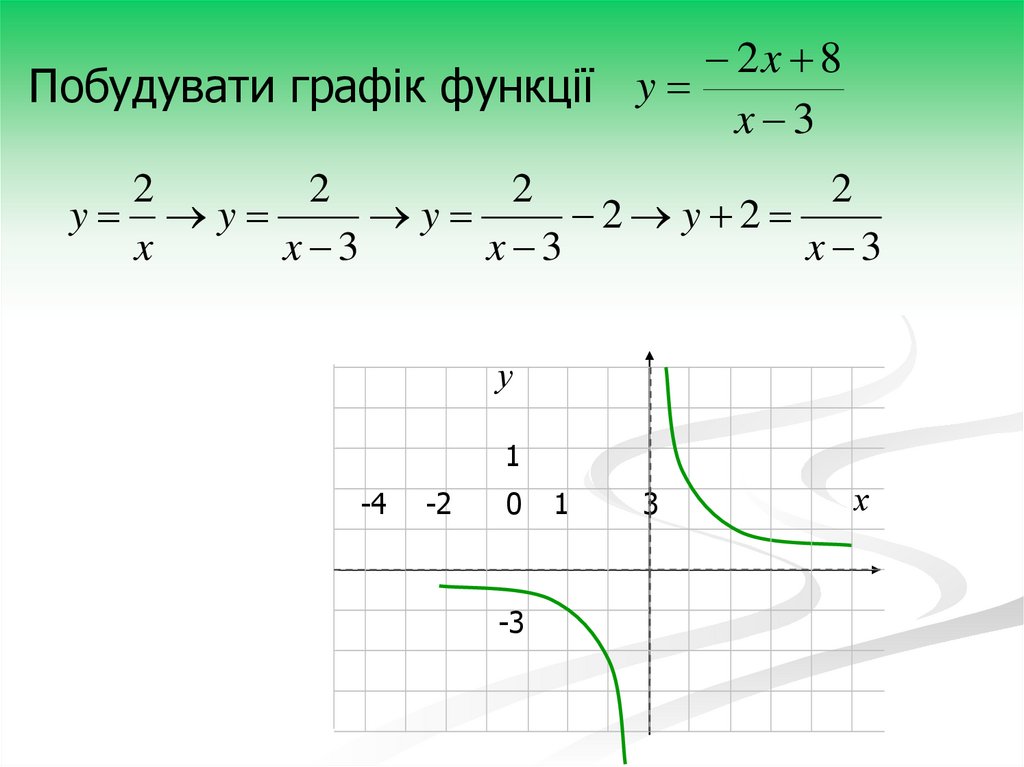
20.

2x 8
Побудувати графік функції y
x 3
2
2
2
2
y y
y
2 y 2
x
x 3
x 3
x 3
у
1
-4
-2
0
-3
1
3
х

21.

Побудова графіків функцій,
що містять знак модуля

22.

Побудова графіка функції
у = |f (x)|
f ( x ), якщо f ( x ) 0;
y | f ( x ) |
f ( x ), якщо f ( x ) 0 .
Графік функції y=|f(x)| можна отримати,
якщо частину графіка функції y=f(x), для
якої f(x)≥0, залишити незмінною, а частину
графіка, для якої f(x)<0 симетрично
відобразити відносно осі абсцис

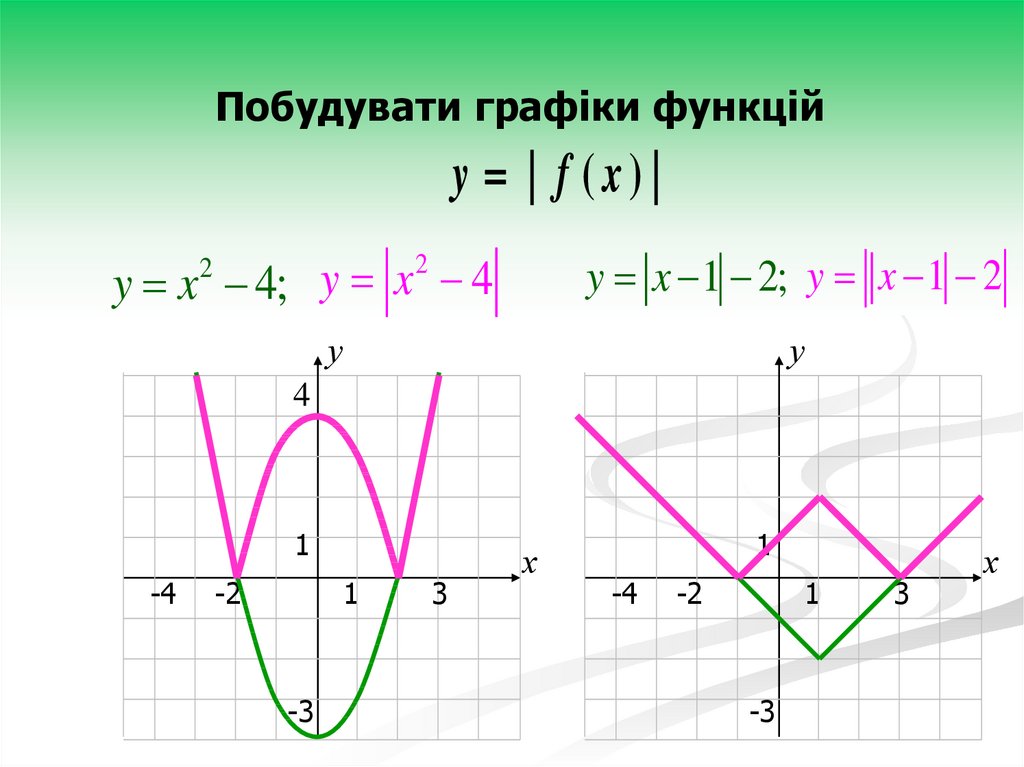
23.

Побудувати графіки функцій
y | f (x) |
y x 1 2; y x 1 2
2
y
x
4
y x 4;
2
у
у
4
1
-4
-2
1
-3
3
х
1
-4
-2
1
-3
3
х

24. Побудова графіка функції у = f (|x|)

f ( x ), якщо x 0;
y f | x |
f ( x ), якщо x 0 .
Графік функції y = f(|x|) можна
отримати, якщо частину графіка функції
y = f(x), що лежить в області x ≥ 0
залишити незмінною, а потім її ж
відобразити симетрично осі ординат в
область х<0

25.

Побудувати графіки функцій
y f | x |
y x 2,5 4; y x 2,5 4;
2
2
y 4 2 x 2 ; y 4 2 x 2
у
у
4
1
-4
-2
1
-3
3
х
1
-4
-2
1
-3
3
х

26.

Умова
1
2
3
y= f (x+a)
Перетворення
Паралельне перенесення осі ординат на a одиниць
вправо, якщо a > 0, і на |a| одиниць вліво, якщо a < 0
Паралельне перенесення осі абсцис на b одиниць вниз,
y= f (x) + b
якщо b>0, та на |b| одиниць вгору, якщо b<0.
y= f (k x)
Стиск в k разів до осі ординат, якщо k > 1, та розтяг в
1/k разів від осі ординат, якщо 0 < k < 1.
y=т f (x)
Розтяг в т разів від осі абсцис, якщо т > 1, та стиск в
1/т разів до осі абсцис, якщо 0 < т < 1.
5
y= f (-x)
Симметричне відображення відносно осі ординат
6
y= f (|x|)
Частина графіка, розташована правіше осі ординат
залишається без змін, а потім симетрично
відображається відносно цієї осі.
7
y= - f (x)
Симметричне відображення відносно осі абсцис
8
y=|f (x)|
Частина графіка, розташована нижче осі абсцис,
симметрично відображається відносно цієї осі, інша
частина залишається без змін.
4

27.

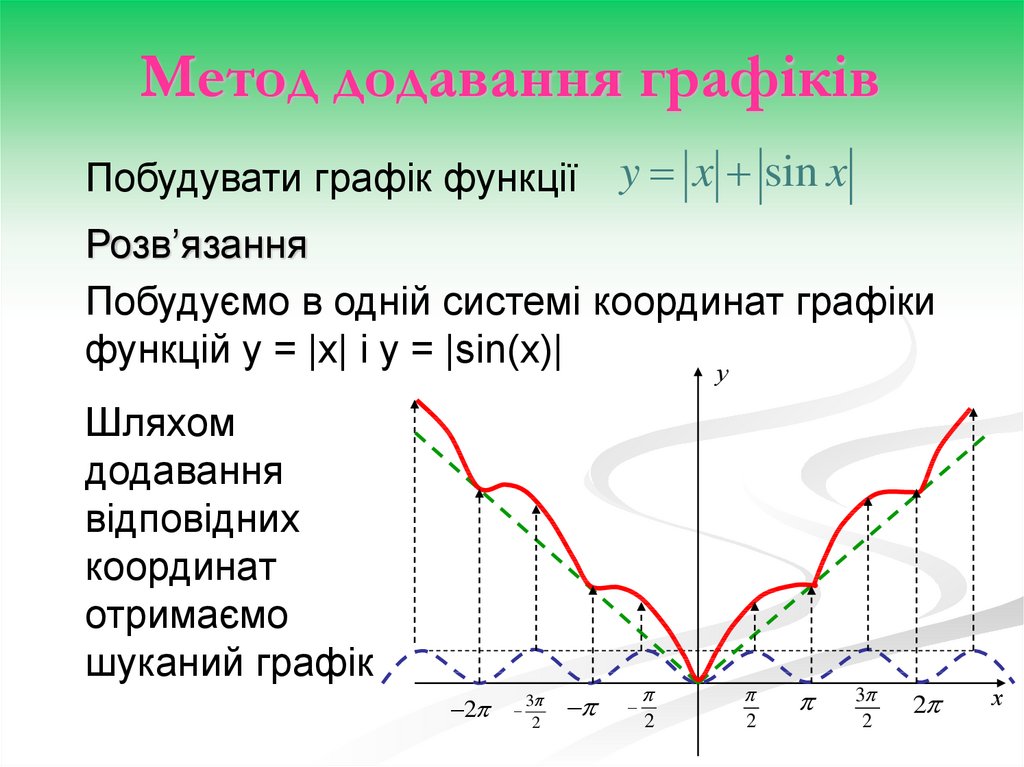
Метод додавання графіків
Побудувати графік функції
y x sin x
Розв’язання
Побудуємо в одній системі координат графіки
функцій у = |x| і y = |sin(x)|
у
Шляхом
додавання
відповідних
координат
отримаємо
шуканий графік
2
3
2
2
2
3
2
2
х

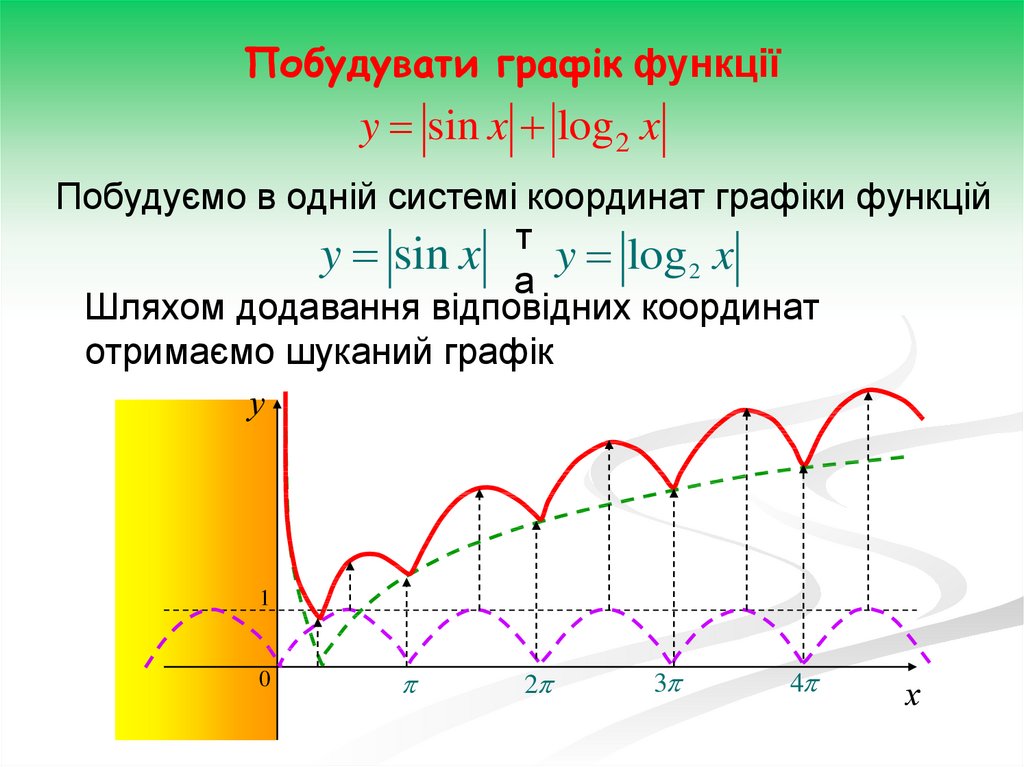
28.

Побудувати графік функції
y sin x log 2 x
Побудуємо в одній системі координат графіки функцій
т
y log 2 x
y sin x
а
Шляхом додавання відповідних координат
отримаємо шуканий графік
у
1
0
2
3
4
х

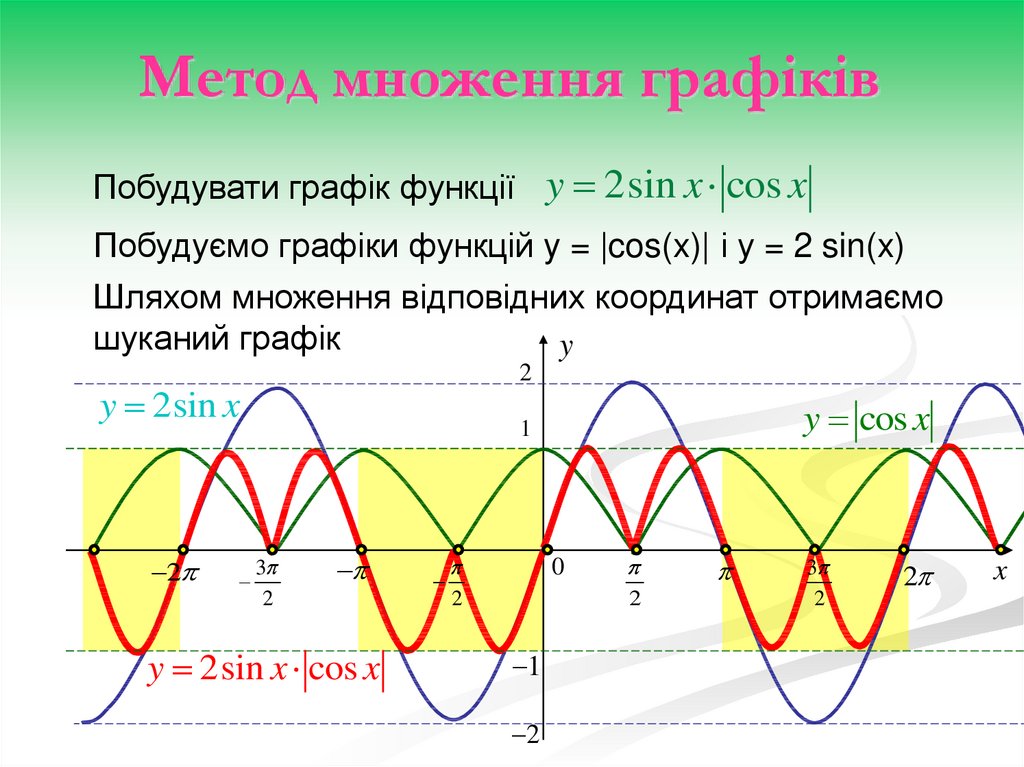
29.

Метод множення графіків
Побудувати графік функції y 2sin x cos x
Побудуємо графіки функцій y = |cos(x)| і у = 2 sin(x)
Шляхом множення відповідних координат отримаємо
шуканий графік
y
2
y 2sin x
2
y cos x
1
3
2
y 2sin x cos x
0
2
2
1
2
3
2
2
x