Тригонометричні функції

1.

2. ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ

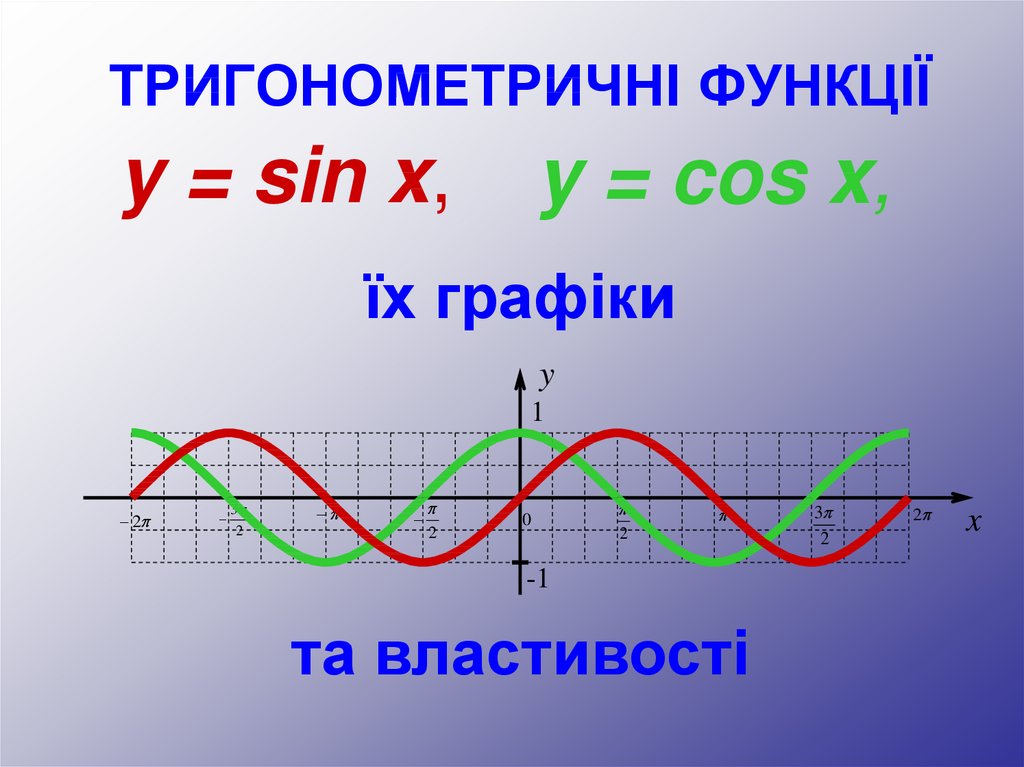
y = sin x,
y = cos x,
їх графіки
y
1
2
3
2
2
0
2
-1
та властивості
3
2
2
x

3. Синус (від лат. sinus) – вигин, кривизна.

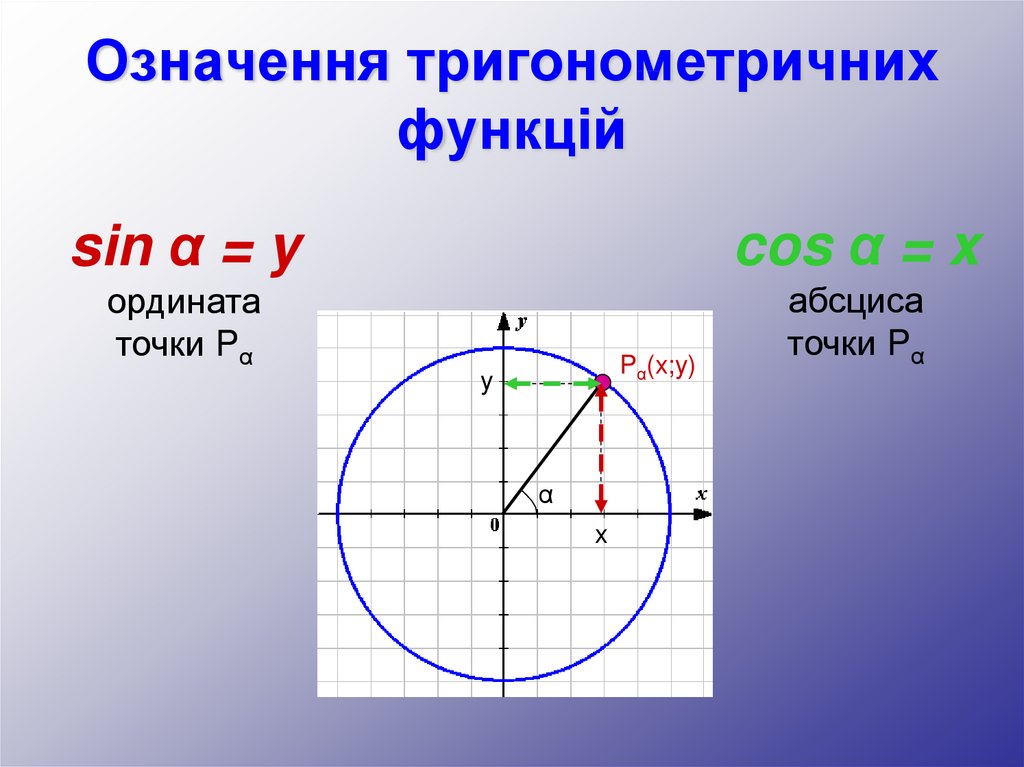
Означення тригонометричних
функцій
sin α = y
cos α = x
ордината
точки Pα
абсциса
точки Pα
Pα(x;y)
y
α
x

4. Означення тригонометричних функцій

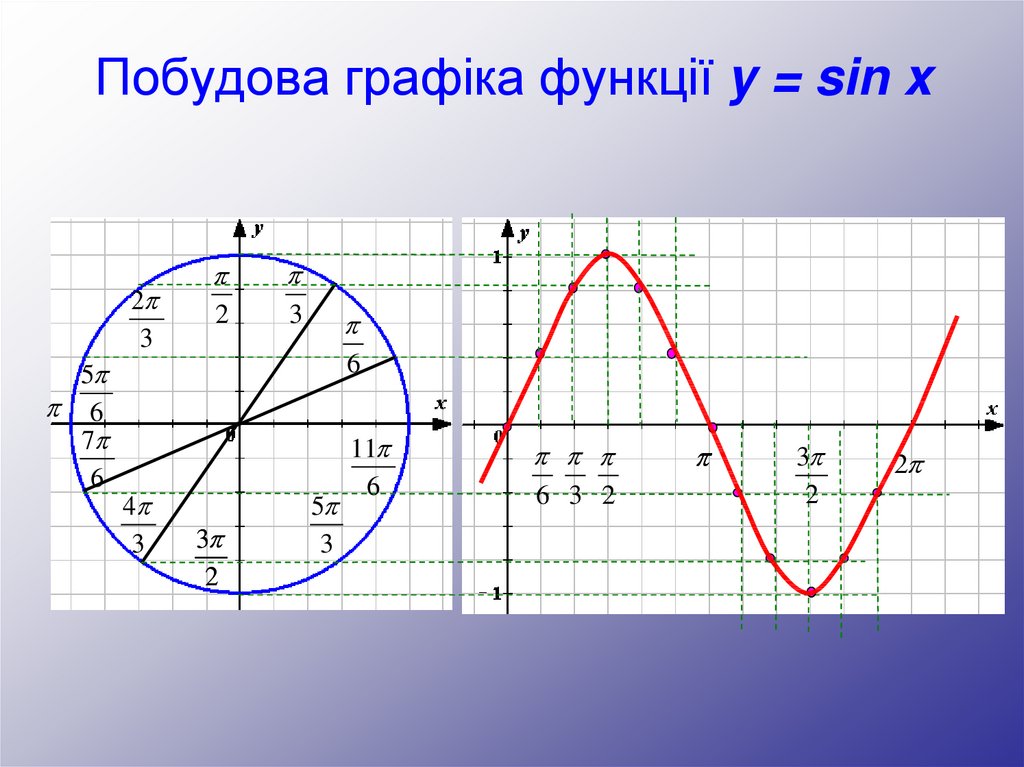
Побудова графіка функції y = sin x
2
3
5
6
7
6
2
3
6
4
3
3
2
5
3
11
6
6 3 2
3
2
2

5. Побудова графіка функції y = sin x

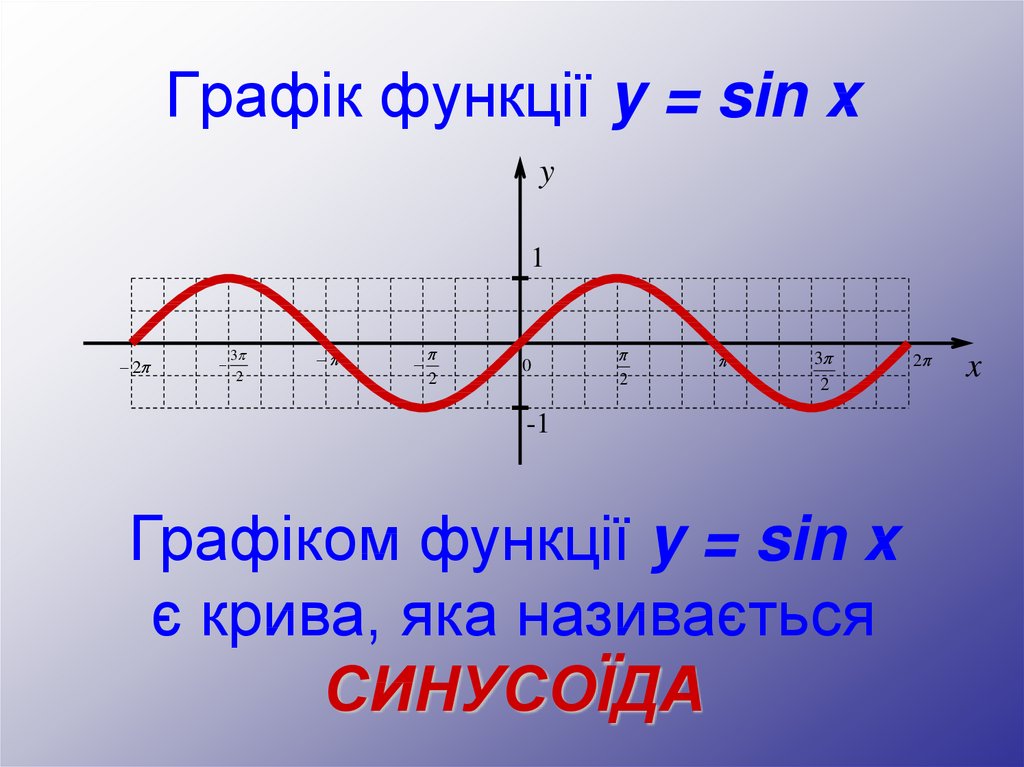
Графік функції y = sin x
y
1
2
3
2
2
0
2
3
2
-1
Графіком функції y = sin x
є крива, яка називається
СИНУСОЇДА
2
x

6. Графік функції y = sin x

Властивості функції y = sin x
y
1
2
3
2
2
0
2
3
2
2
x
-1
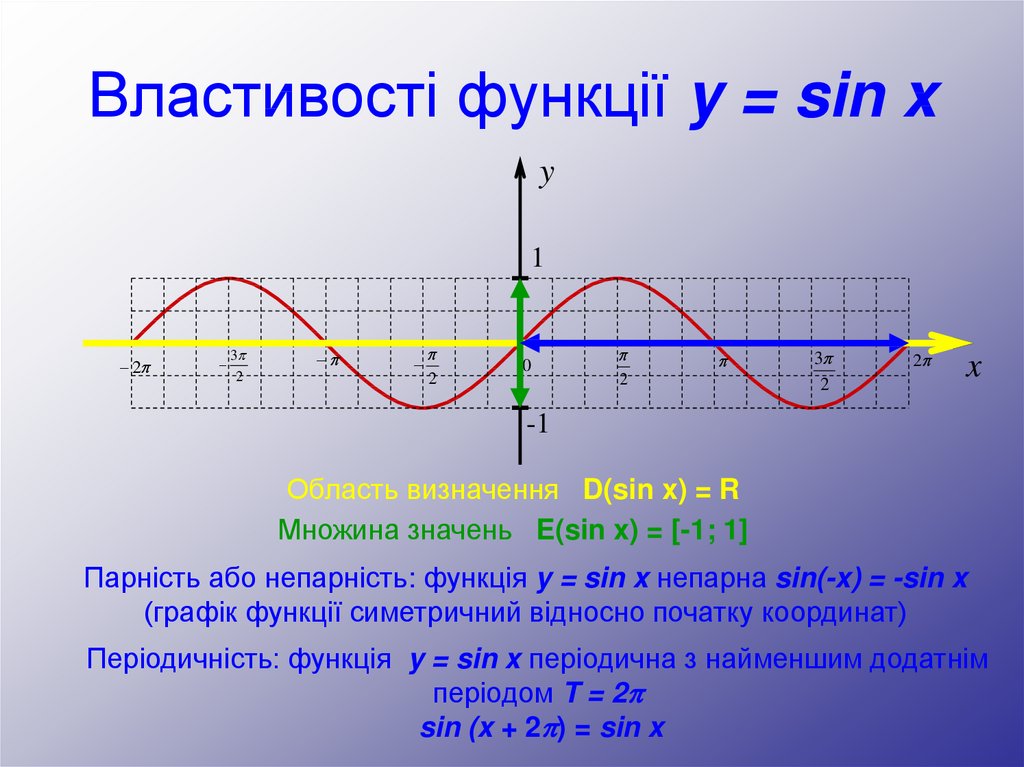
Область визначення D(sin x) = R
Множина значень E(sin x) = [-1; 1]
Парність або непарність: функція y = sin x непарна sin(-x) = -sin x
(графік функції симетричний відносно початку координат)
Періодичність: функція y = sin x періодична з найменшим додатнім
періодом T = 2
sin (x + 2 ) = sin x

7. Властивості функції y = sin x

y
1
2
3
2
2
0
2
3
2
2
-1
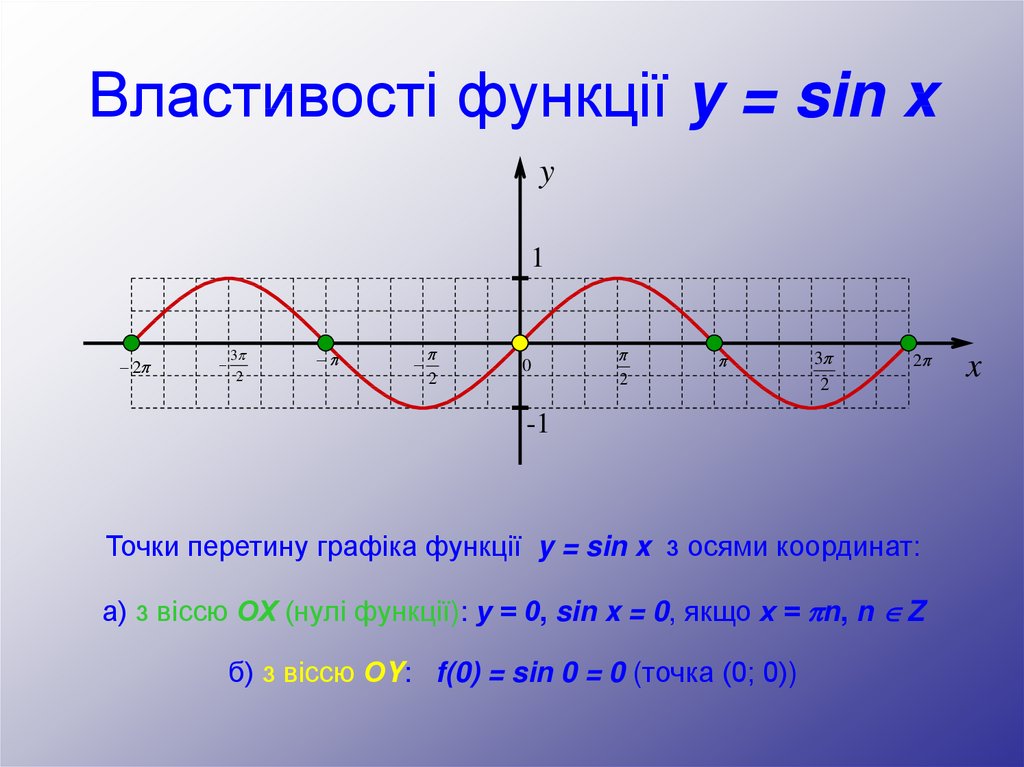
Точки перетину графіка функції y = sin x з осями координат:
а) з віссю ОХ (нулі функції): у = 0, sin x = 0, якщо х = n, n Z
б) з віссю ОY: f(0) = sin 0 = 0 (точка (0; 0))
x

8. Властивості функції y = sin x

y
1
2
3
2
2
0
2
-1
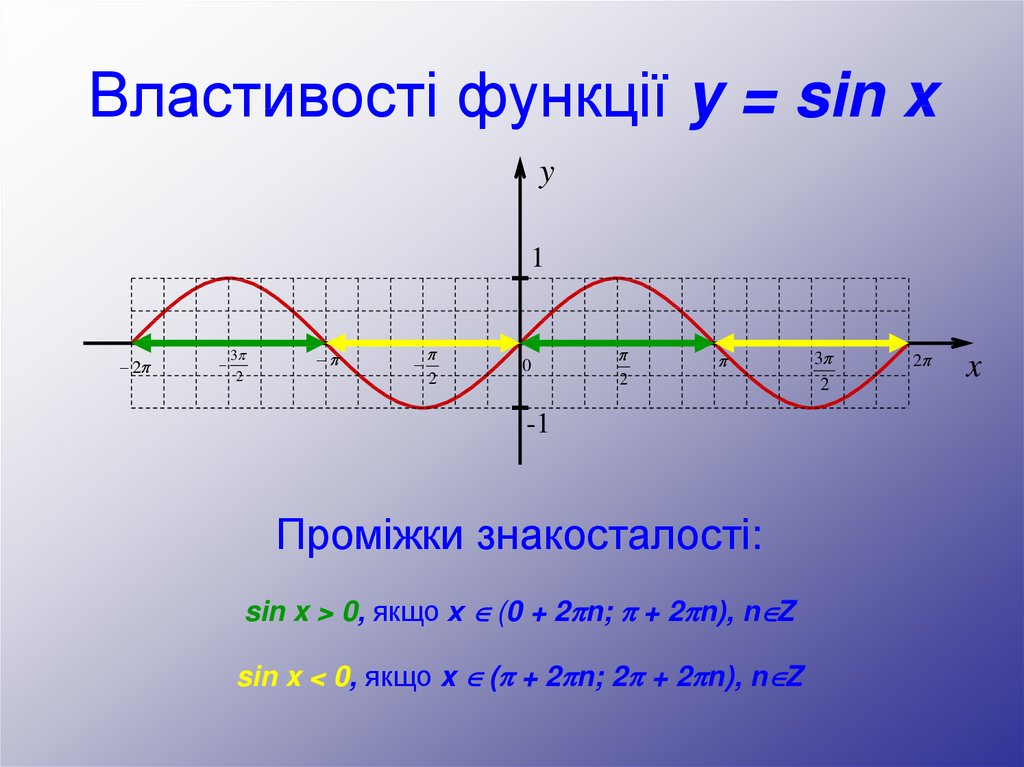
Проміжки знакосталості:
sin x > 0, якщо х (0 + 2 n; + 2 n), n Z
sin x < 0, якщо x ( + 2 n; 2 + 2 n), n Z
3
2
2
x

9. Властивості функції y = sin x

y
1
2
3
2
2
0
2
2
-1
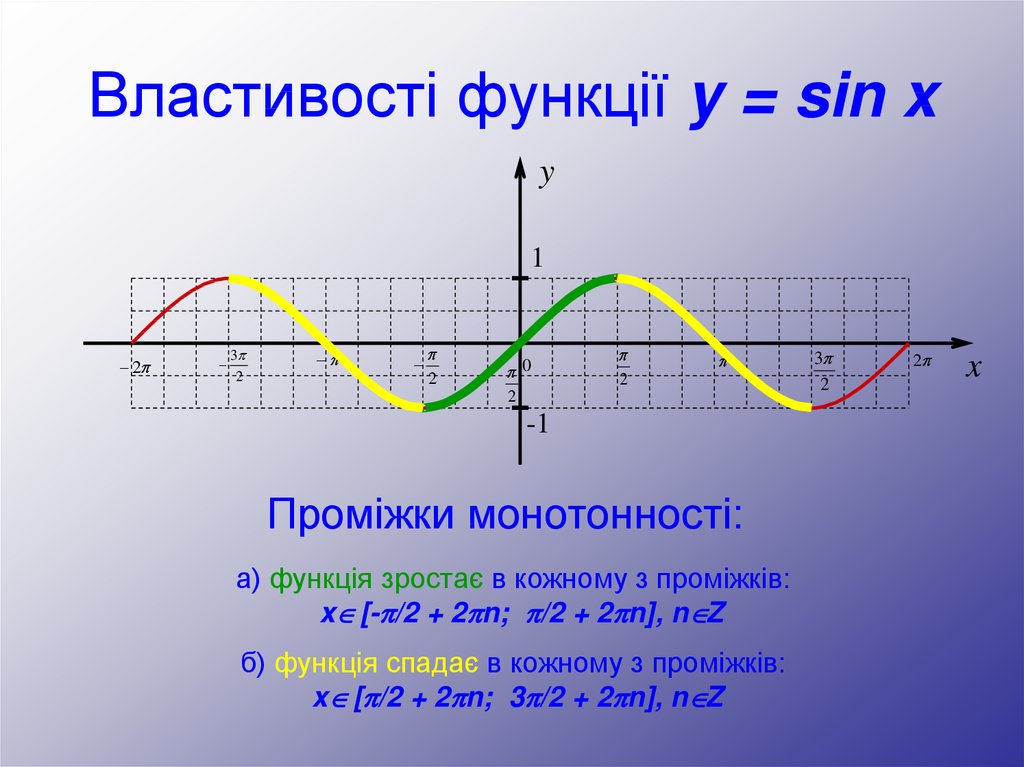
Проміжки монотонності:
а) функція зростає в кожному з проміжків:
x [- /2 + 2 n; /2 + 2 n], n Z
б) функція спадає в кожному з проміжків:
x [ /2 + 2 n; 3 /2 + 2 n], n Z
3
2
2
x

10. Властивості функції y = sin x

y
1
2
3
2
2
0
2
-1
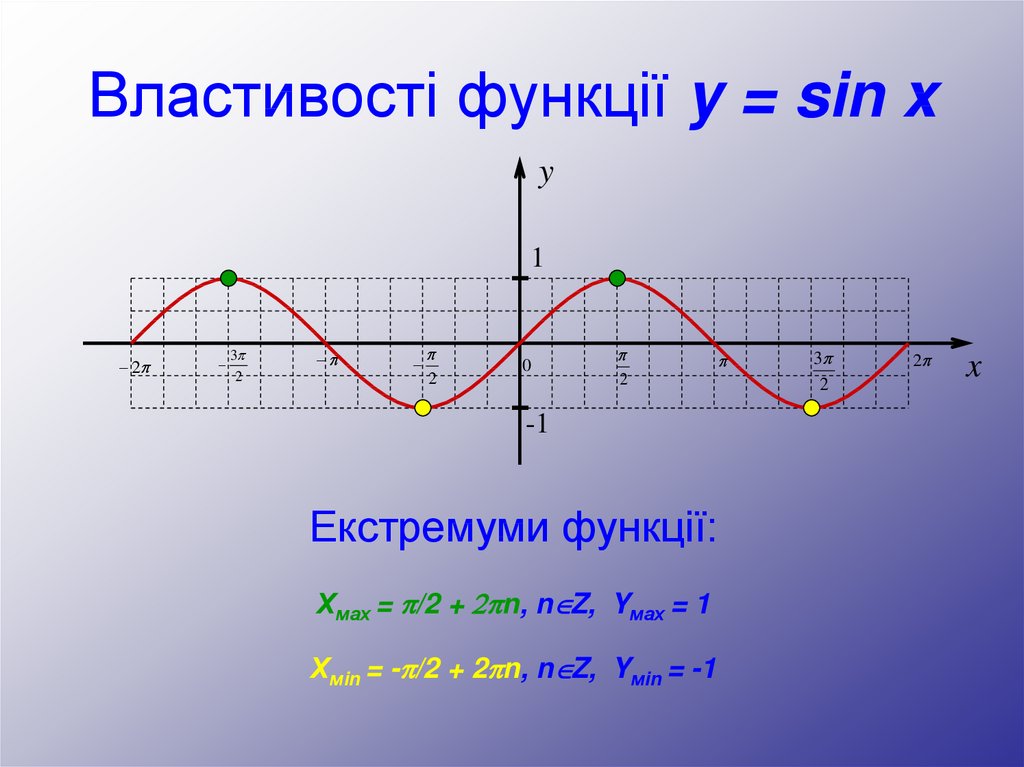
Екстремуми функції:
Хмах = /2 + 2 n, n Z, Yмах = 1
Хмin = - /2 + 2 n, n Z, Yмin = -1
3
2
2
x

11. Властивості функції y = sin x

Перетворення графіків функції y = sin x
Побудувати графік функції y = sin (x + /6)
y
1
2
3
2
2
0
2
3
2
2
-1
Для побудови графіка функції y = sin (x + а)
необхідно графік функції y = sin x здвинути вздовж осі OX на а
одиниць вліво
x

12. Перетворення графіків функції y = sin x

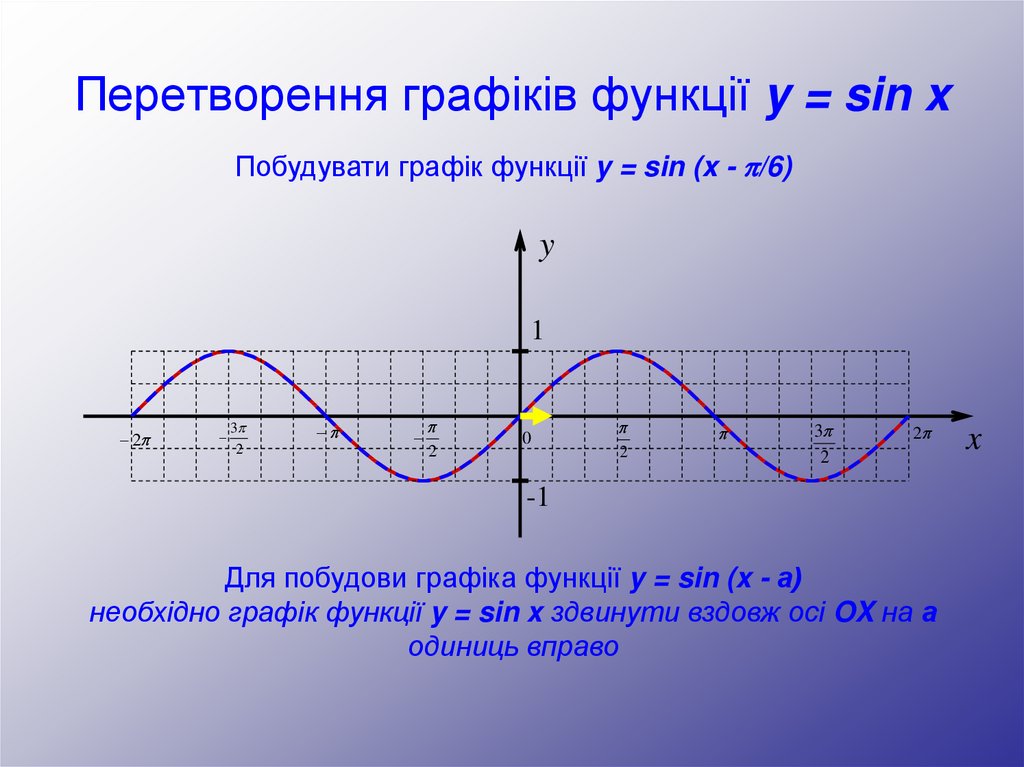
Побудувати графік функції y = sin (x - /6)
y
1
2
3
2
2
0
2
3
2
2
-1
Для побудови графіка функції y = sin (x - а)
необхідно графік функції y = sin x здвинути вздовж осі OX на а
одиниць вправо
x

13. Перетворення графіків функції y = sin x

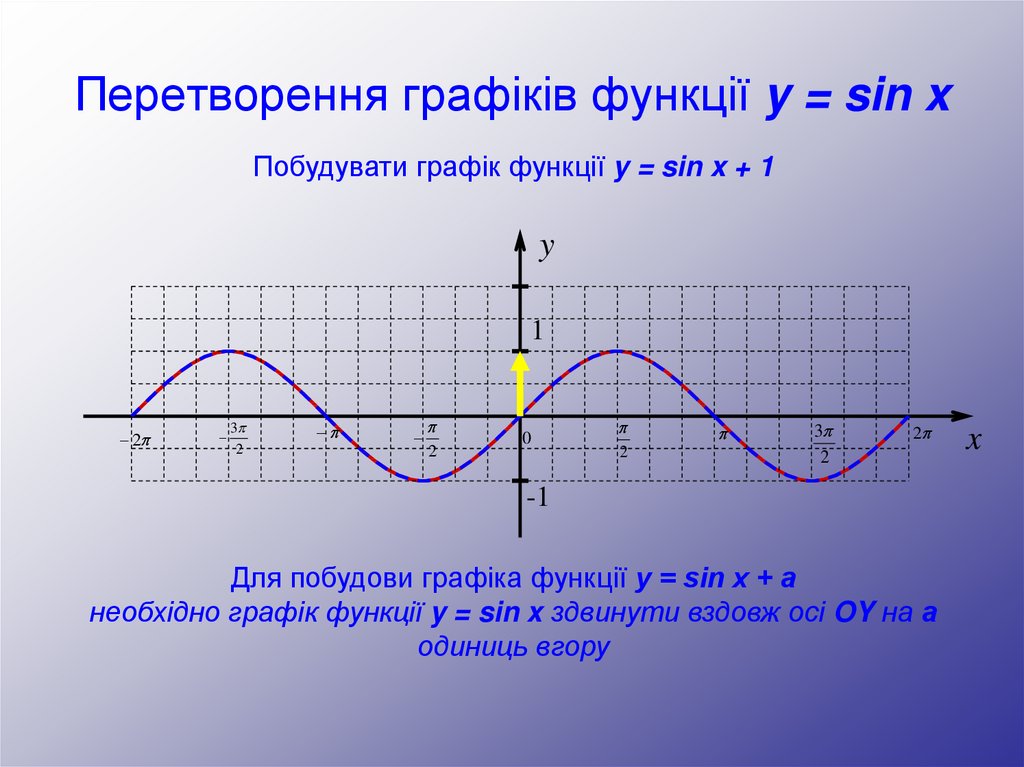
Побудувати графік функції y = sin x + 1
y
1
2
3
2
2
0
2
3
2
2
-1
Для побудови графіка функції y = sin x + а
необхідно графік функції y = sin x здвинути вздовж осі OY на а
одиниць вгору
x

14. Перетворення графіків функції y = sin x

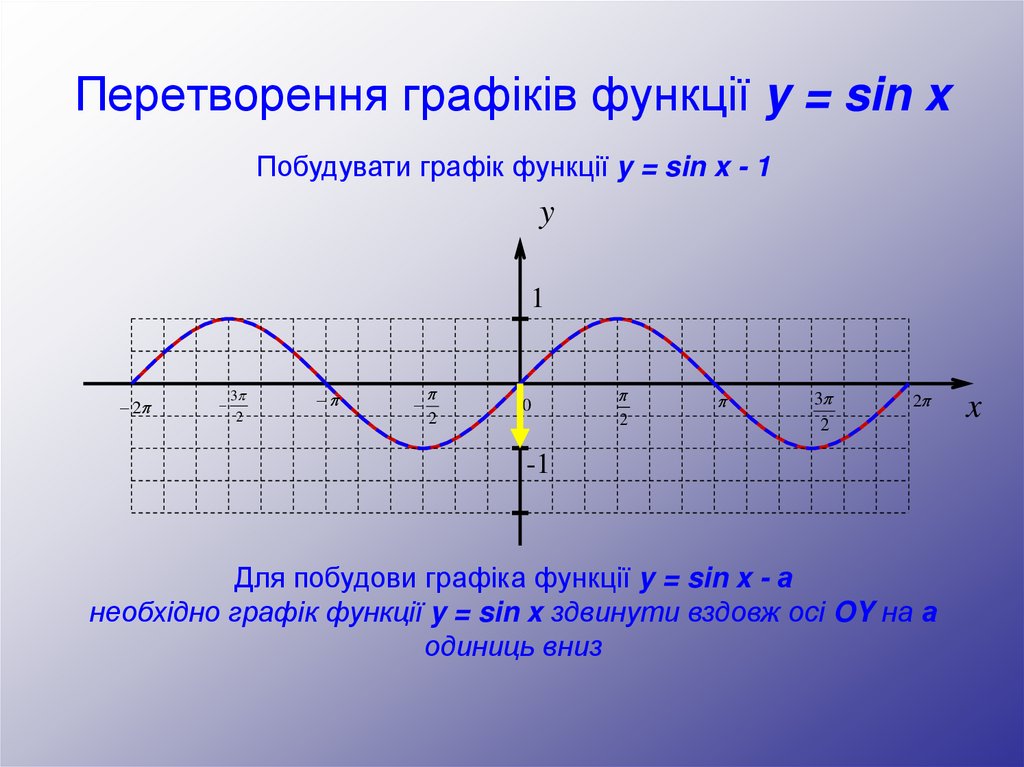
Побудувати графік функції y = sin x - 1
y
1
2
3
2
2
0
2
3
2
2
-1
Для побудови графіка функції y = sin x - а
необхідно графік функції y = sin x здвинути вздовж осі OY на а
одиниць вниз
x

15. Перетворення графіків функції y = sin x

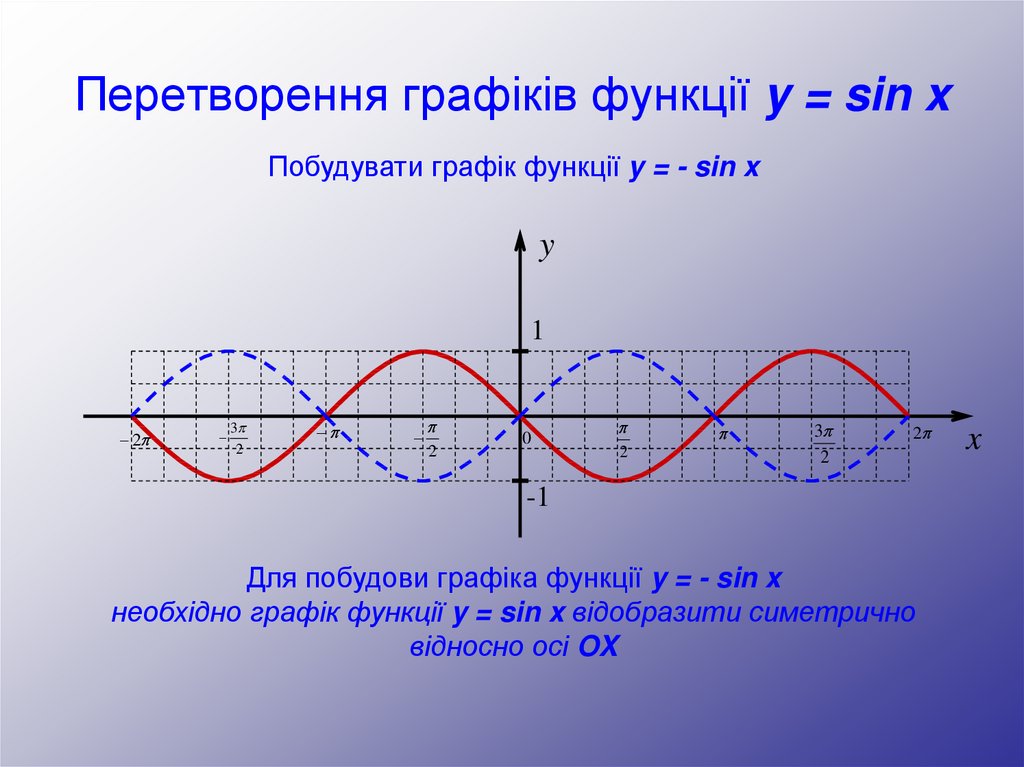
Побудувати графік функції y = - sin x
y
1
2
3
2
2
0
2
3
2
2
-1
Для побудови графіка функції y = - sin x
необхідно графік функції y = sin x відобразити симетрично
відносно осі OX
x

16. Перетворення графіків функції y = sin x

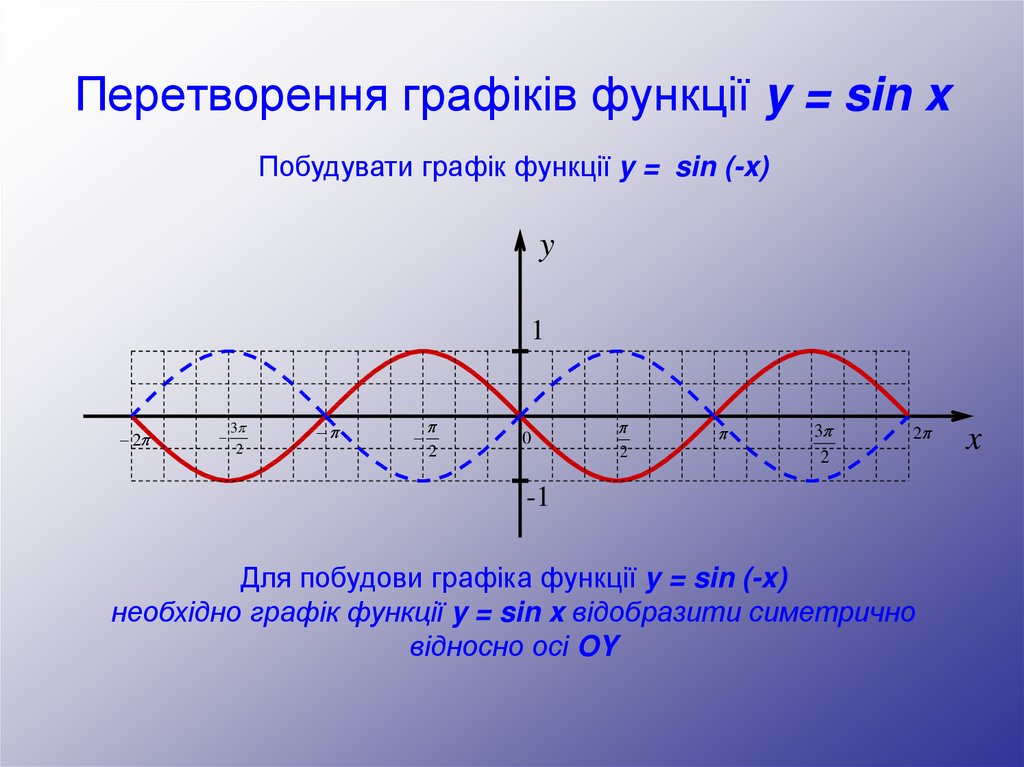
Побудувати графік функції y = sin (-x)
y
1
2
3
2
2
0
2
3
2
2
-1
Для побудови графіка функції y = sin (-x)
необхідно графік функції y = sin x відобразити симетрично
відносно осі OY
x

17. Перетворення графіків функції y = sin x

Побудувати графік функції y = | sin x |
y
1
2
3
2
2
0
2
3
2
2
-1
Для побудови графіка функції y = | sin x |
необхідно додатну частину графіка функції y = sin x залишити
незмінною, а від'ємну частину відобразити симетрично відносно
осі OX
x

18. Перетворення графіків функції y = sin x

Побудувати графік функції y = sin | x |
y
1
2
3
2
2
0
2
3
2
2
-1
Для побудови графіка функції y = sin | x |
необхідно побудувати графік функції y = sin x при x≥0, а для x<0
побудувати графік, який буде симетричний для вже побудованого
графіка відносно осі OY
x

19. Перетворення графіків функції y = sin x

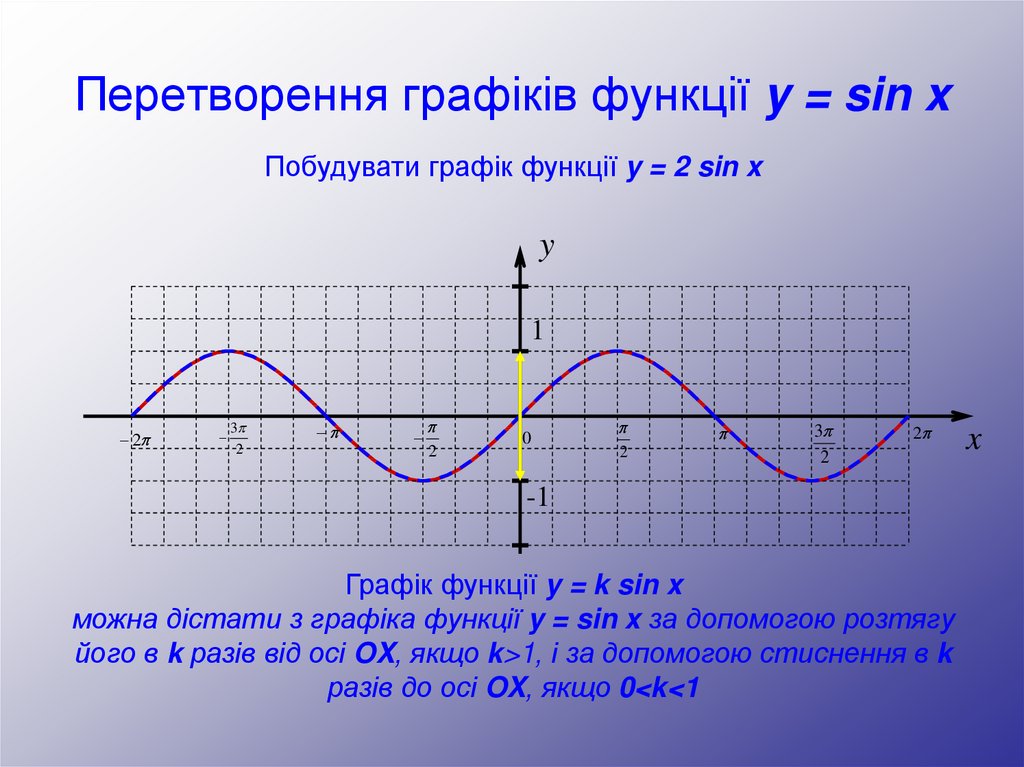
Побудувати графік функції y = 2 sin x
y
1
2
3
2
2
0
2
3
2
2
-1
Графік функції y = k sin x
можна дістати з графіка функції y = sin x за допомогою розтягу
його в k разів від осі OX, якщо k>1, і за допомогою стиснення в k
разів до осі OX, якщо 0<k<1
x

20. Перетворення графіків функції y = sin x

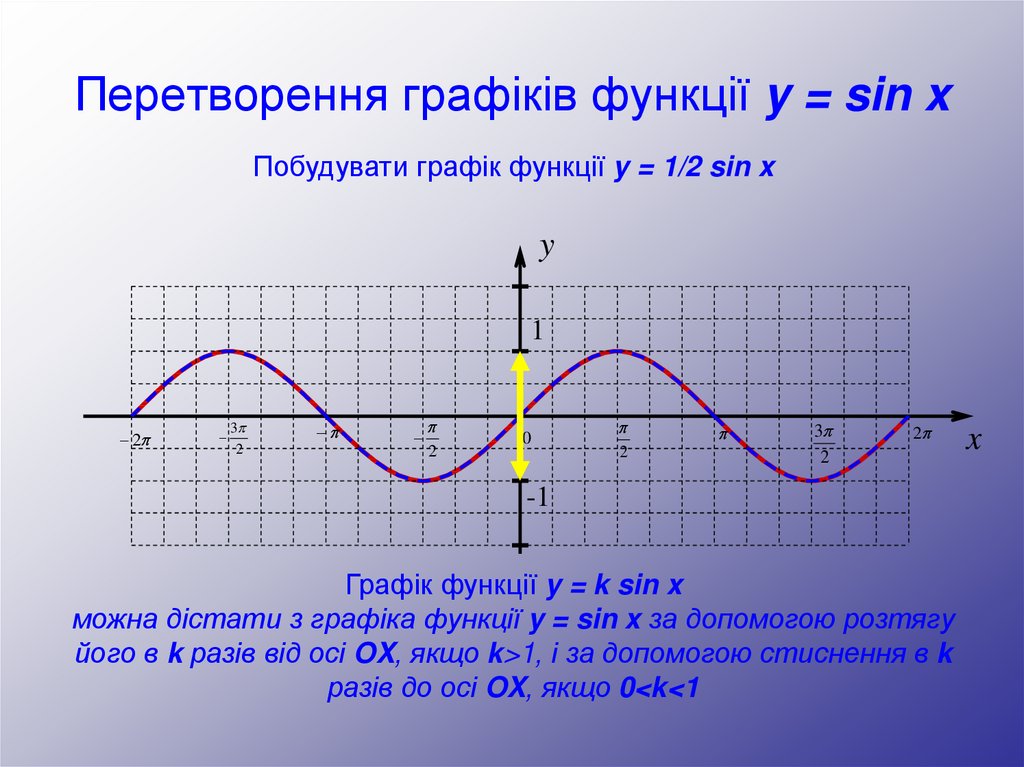
Побудувати графік функції y = 1/2 sin x
y
1
2
3
2
2
0
2
3
2
2
-1
Графік функції y = k sin x
можна дістати з графіка функції y = sin x за допомогою розтягу
його в k разів від осі OX, якщо k>1, і за допомогою стиснення в k
разів до осі OX, якщо 0<k<1
x

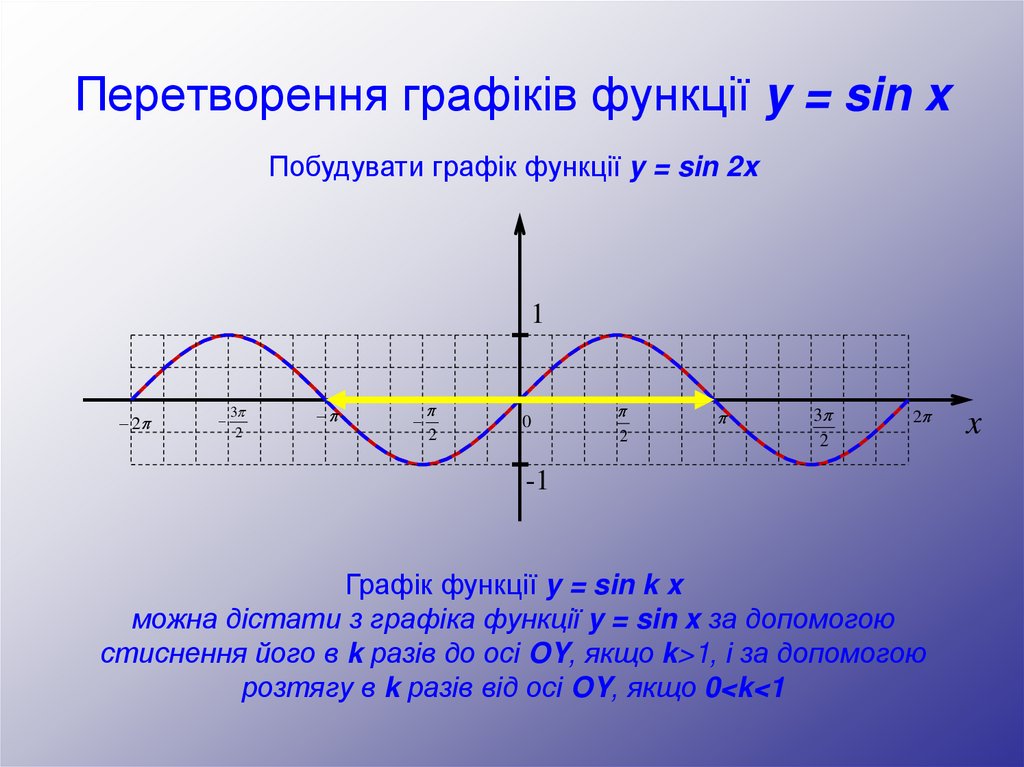
21. Перетворення графіків функції y = sin x

Побудувати графік функції y = sin 2x
1
2
3
2
2
0
2
3
2
2
-1
Графік функції y = sin k x
можна дістати з графіка функції y = sin x за допомогою
стиснення його в k разів до осі OY, якщо k>1, і за допомогою
розтягу в k разів від осі OY, якщо 0<k<1
x

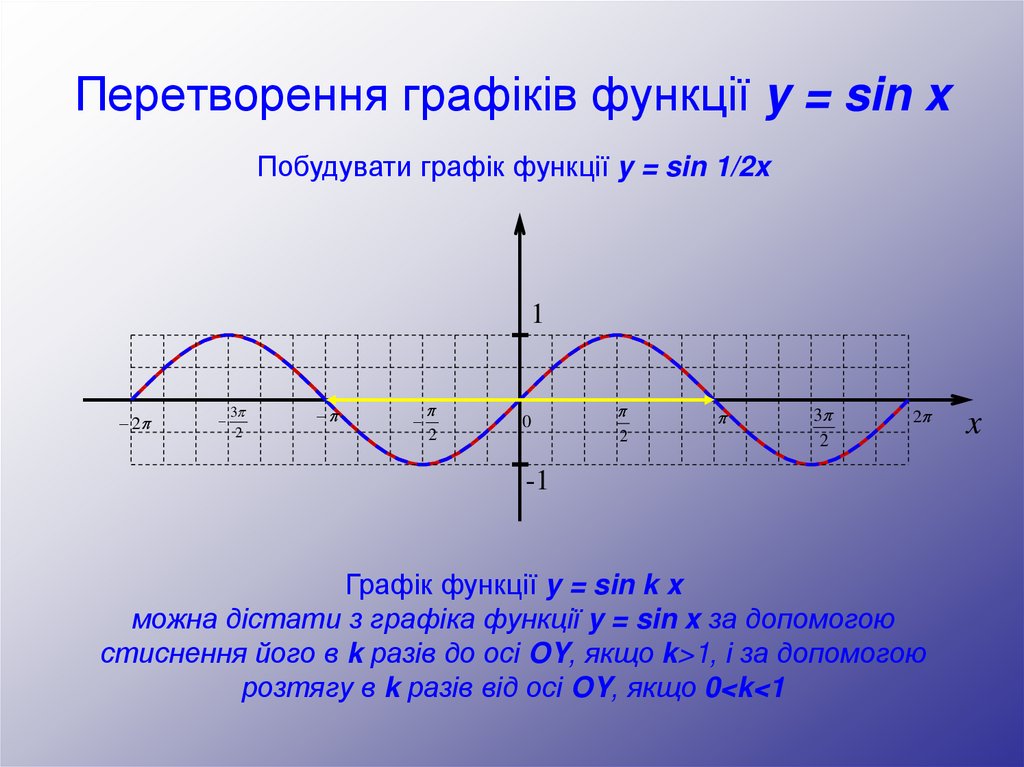
22. Перетворення графіків функції y = sin x

Побудувати графік функції y = sin 1/2x
1
2
3
2
2
0
2
3
2
2
-1
Графік функції y = sin k x
можна дістати з графіка функції y = sin x за допомогою
стиснення його в k разів до осі OY, якщо k>1, і за допомогою
розтягу в k разів від осі OY, якщо 0<k<1
x

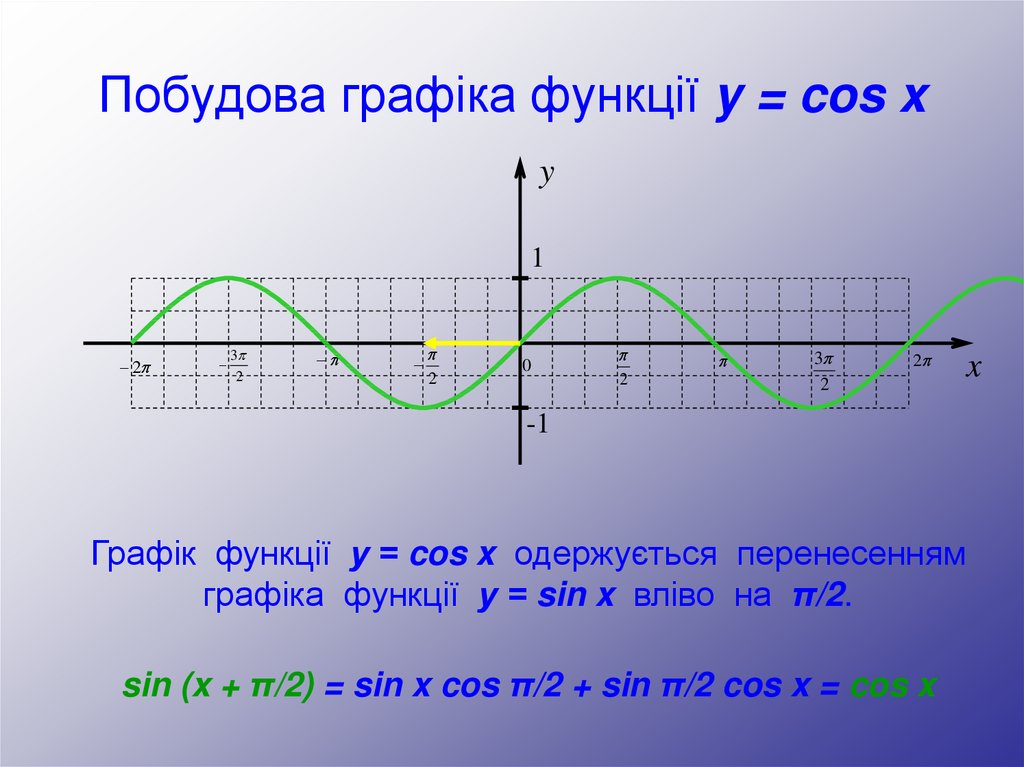
23. Перетворення графіків функції y = sin x

Побудова графіка функції y = cos x
y
1
2
3
2
2
0
2
3
2
2
x
-1
Графік функції у = cos x одержується перенесенням
графіка функції у = sin x вліво на π/2.
sin (x + π/2) = sin x cos π/2 + sin π/2 cos x = cos x

24. Побудова графіка функції y = cos x

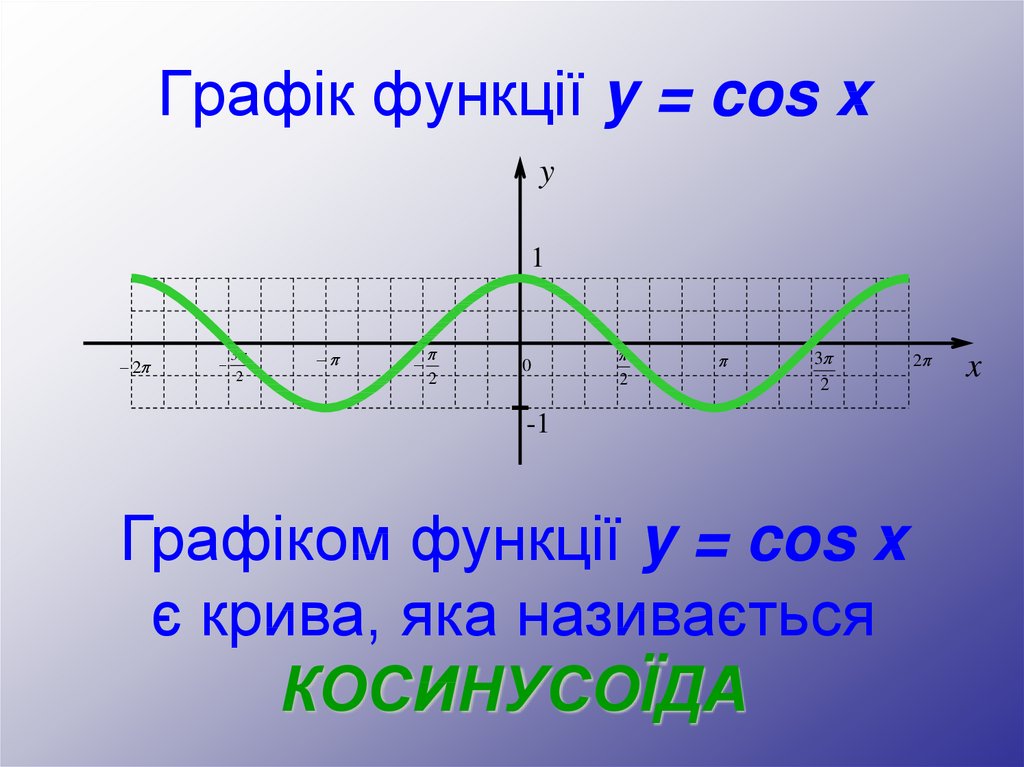
Графік функції y = cos x
y
1
2
3
2
2
0
2
3
2
-1
Графіком функції y = cos x
є крива, яка називається
КОСИНУСОЇДА
2
x

25. Графік функції y = cos x

Властивості функції y = cos x
y
1
2
3
2
2
0
2
3
2
2
-1
Область визначення D(cos x) = R
Множина значень E(cos x) = [-1; 1]
Парність або непарність: функція y = cos x парна cos(-x) = cos x
(графік функції симетричний відносно осі OY)
Періодичність: функція y = cos x періодична з найменшим
додатнім періодом T = 2
cos (x + 2 ) = cos x
x

26. Властивості функції y = cos x

y
1
2
3
2
2
0
2
3
2
2
-1
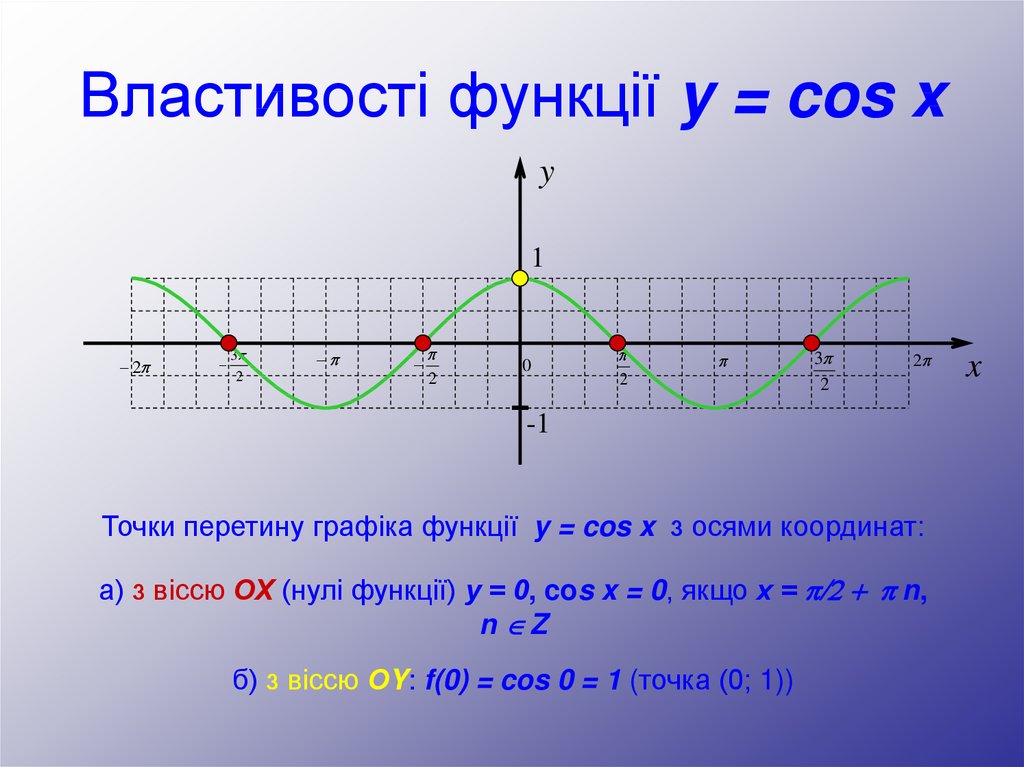
Точки перетину графіка функції y = cos x з осями координат:
а) з віссю ОХ (нулі функції) у = 0, cos x = 0, якщо х = /2 + n,
n Z
б) з віссю ОY: f(0) = cos 0 = 1 (точка (0; 1))
x

27. Властивості функції y = cos x

y
1
2
3
2
2
0
2
3
2
-1
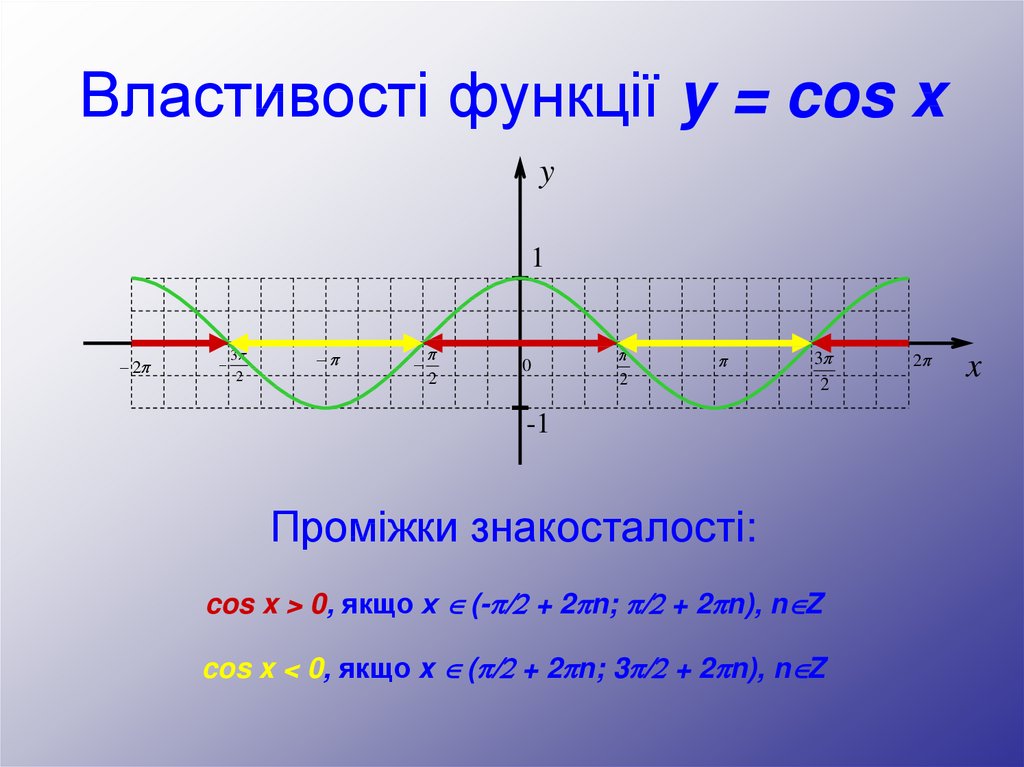
Проміжки знакосталості:
cos x > 0, якщо х (- /2 + 2 n; /2 + 2 n), n Z
cos x < 0, якщо x ( /2 + 2 n; 3 /2 + 2 n), n Z
2
x

28. Властивості функції y = cos x

y
1
2
3
2
2
0
2
-1
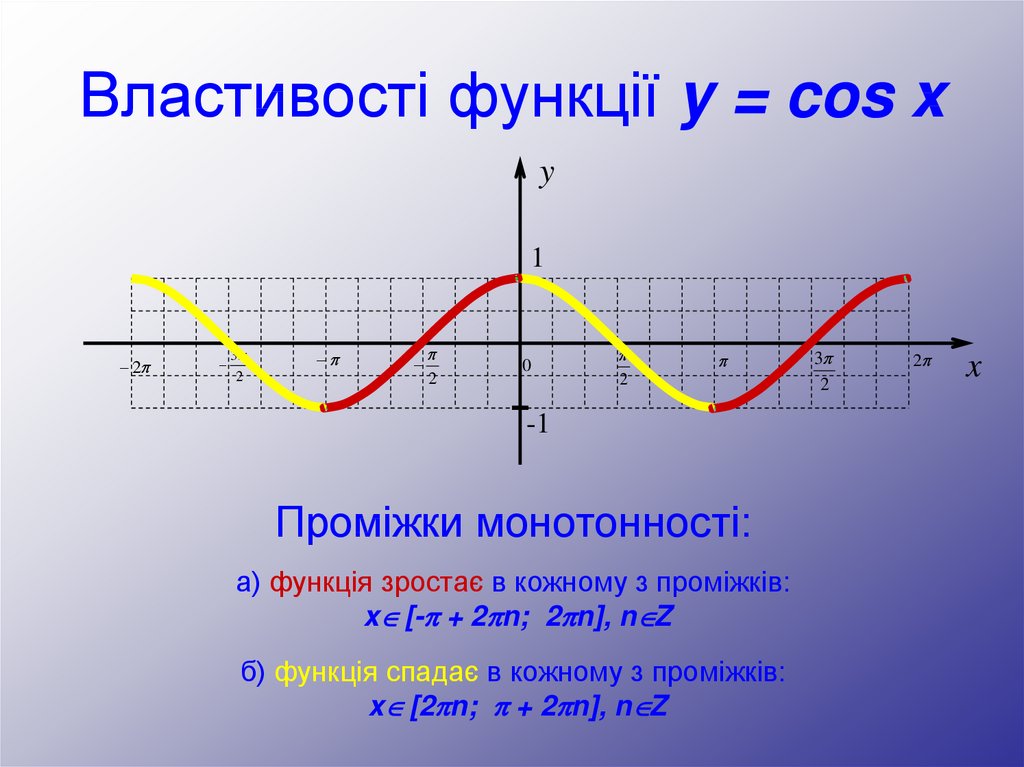
Проміжки монотонності:
а) функція зростає в кожному з проміжків:
x [- + 2 n; 2 n], n Z
б) функція спадає в кожному з проміжків:
x [2 n; + 2 n], n Z
3
2
2
x

29. Властивості функції y = cos x

y
1
2
3
2
2
0
2
-1
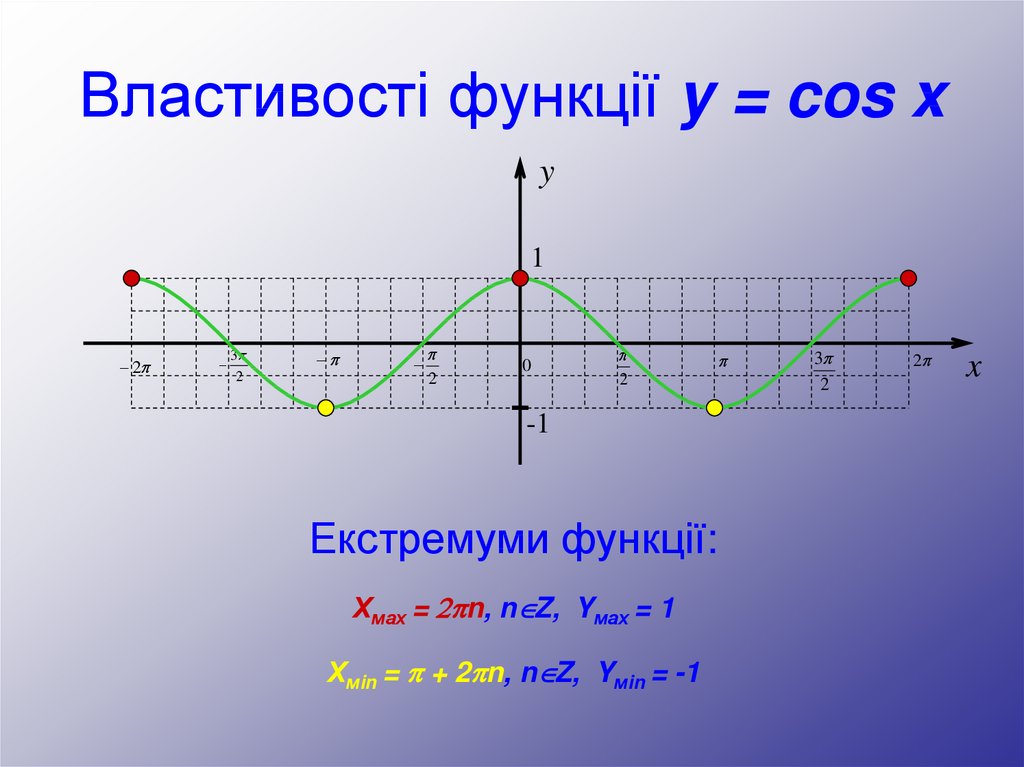
Екстремуми функції:
Хмах = 2 n, n Z, Yмах = 1
Хмin = + 2 n, n Z, Yмin = -1
3
2
2
x

30. Властивості функції y = cos x

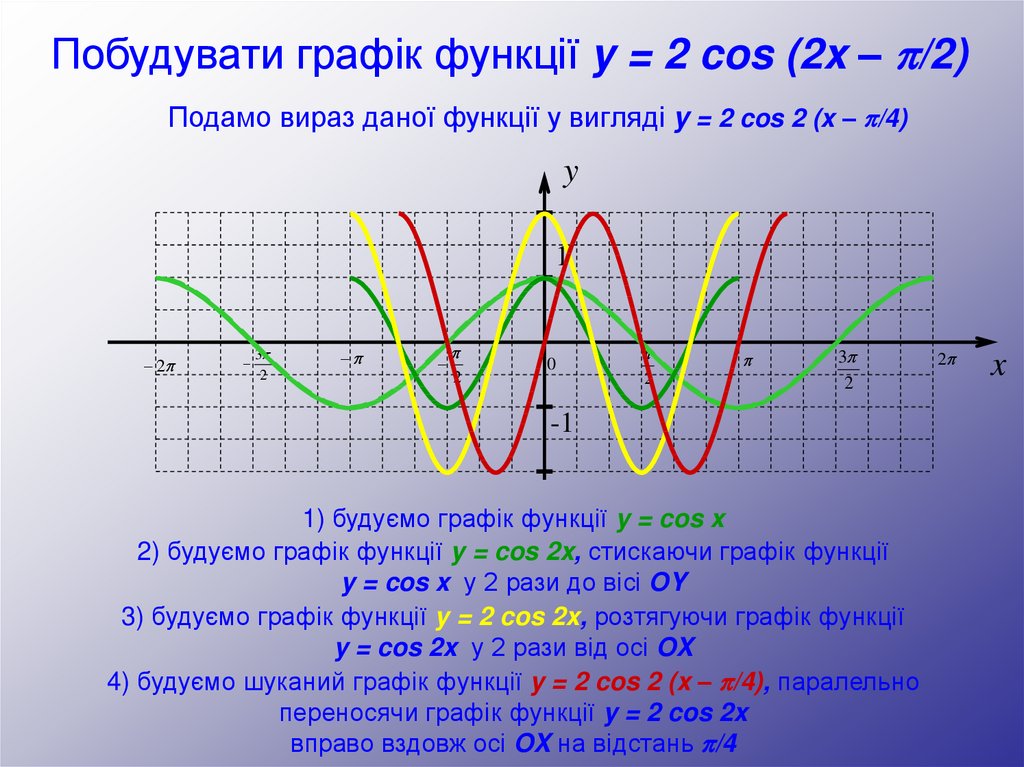
Побудувати графік функції y = 2 cos (2x – /2)
Подамо вираз даної функції у вигляді y = 2 cos 2 (x – /4)
y
1
2
3
2
2
0
2
3
2
-1
1) будуємо графік функції y = cos x
2) будуємо графік функції y = cos 2x, стискаючи графік функції
y = cos x у 2 рази до вісі OY
3) будуємо графік функції y = 2 cos 2x, розтягуючи графік функції
y = cos 2x у 2 рази від осі OX
4) будуємо шуканий графік функції y = 2 cos 2 (x – /4), паралельно
переносячи графік функції y = 2 cos 2x
вправо вздовж осі OX на відстань /4
2
x

31.

32.

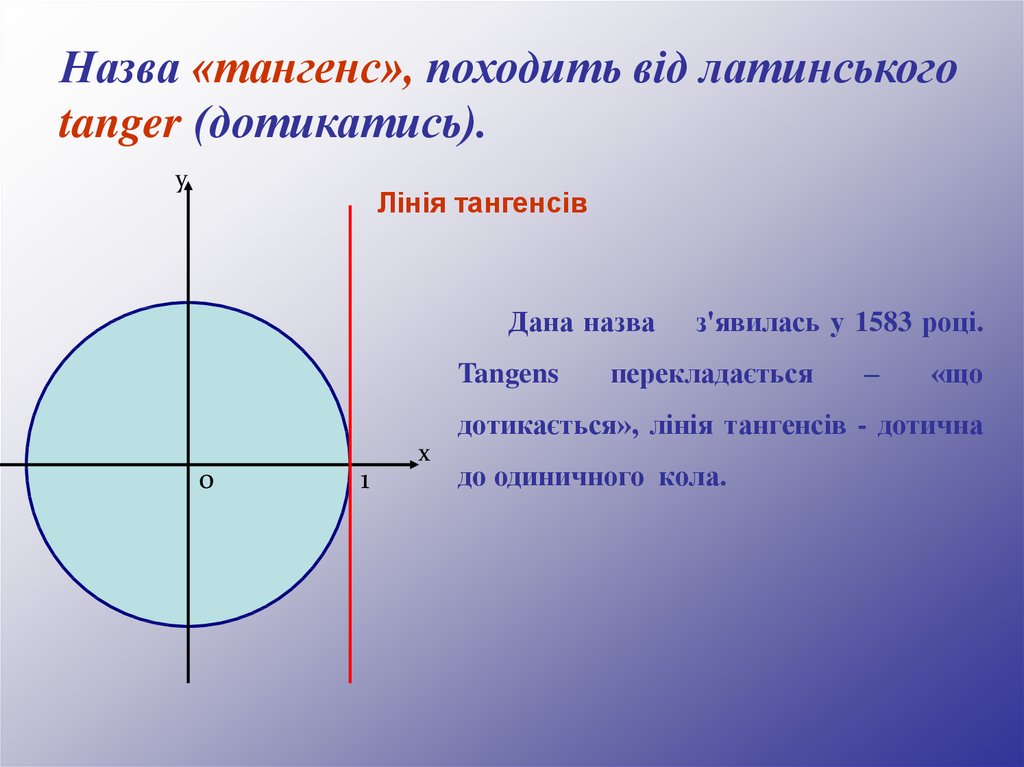
Назва «тангенс», походить від латинського
tanger (дотикатись).
у
Лінія тангенсів
Дана назва
Tangens
з'явилась у 1583 році.
перекладається
–
«що
дотикається», лінія тангенсів - дотична
0
1
х
до одиничного кола.

33.

Означення функції y = tg x
у
Pα(x;y)
y
α
x
0
1
х
y
tg
x
Тангенсом
кута
називають
відношення ординати точки Pα(x;y) до її
абсциси.

34.

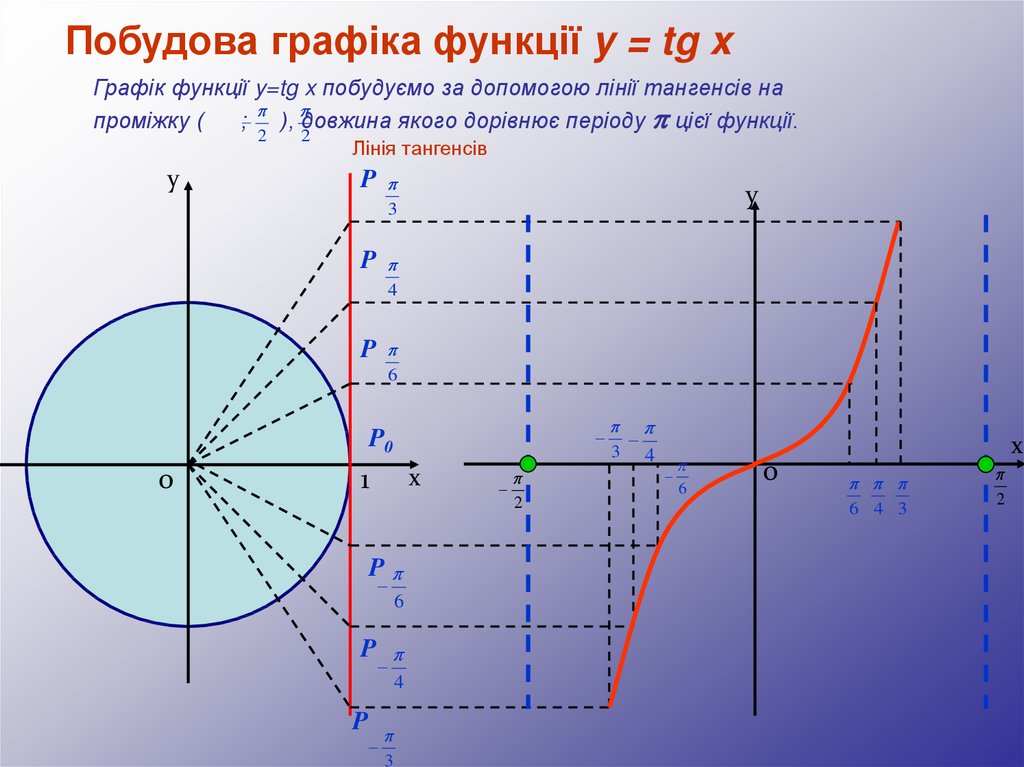
Побудова графіка функції y = tg x
Графік функції y=tg x побудуємо за допомогою лінії тангенсів на
проміжку (
; ), довжина якого дорівнює періоду цієї функції.
2
у
2
Лінія тангенсів
P
у
3
P
4
P
6
P0
0
х
1
P
P
P
6
3
4
2
3
4
6
0
х
6 4 3
2

35.

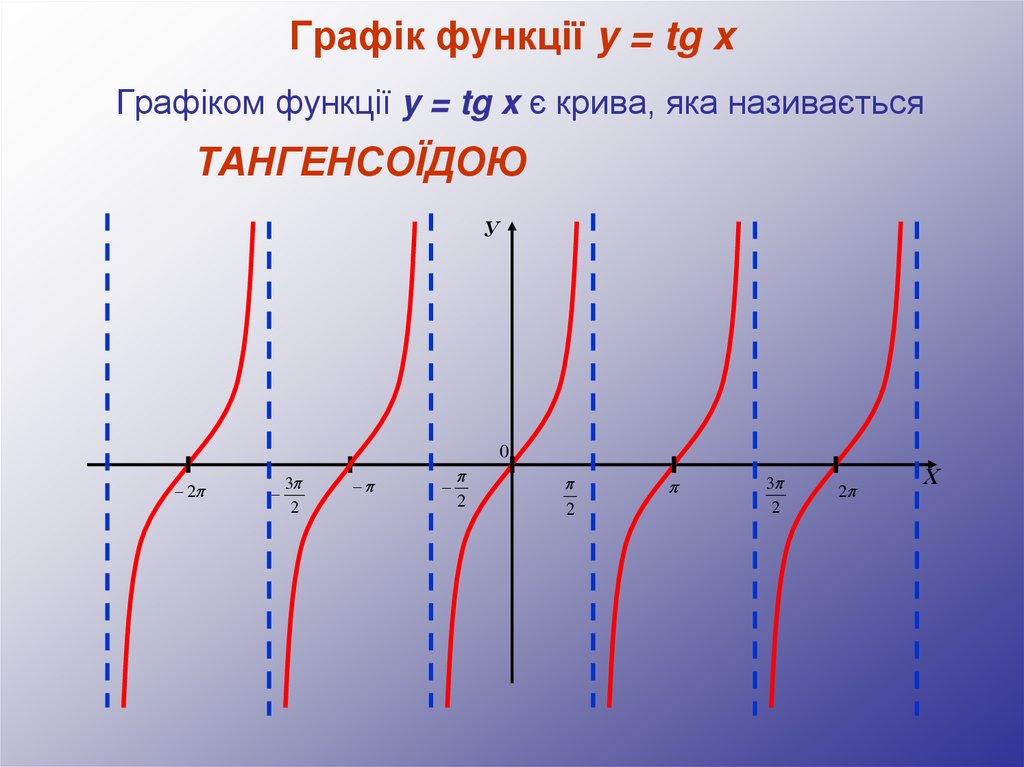
Графік функції y = tg x
Графіком функції y = tg x є крива, яка називається
ТАНГЕНСОЇДОЮ
У
0
2
3
2
2
2
3
2
2
Х

36. Графік функції y = tg x Графіком функції y = tg x є крива, яка називається

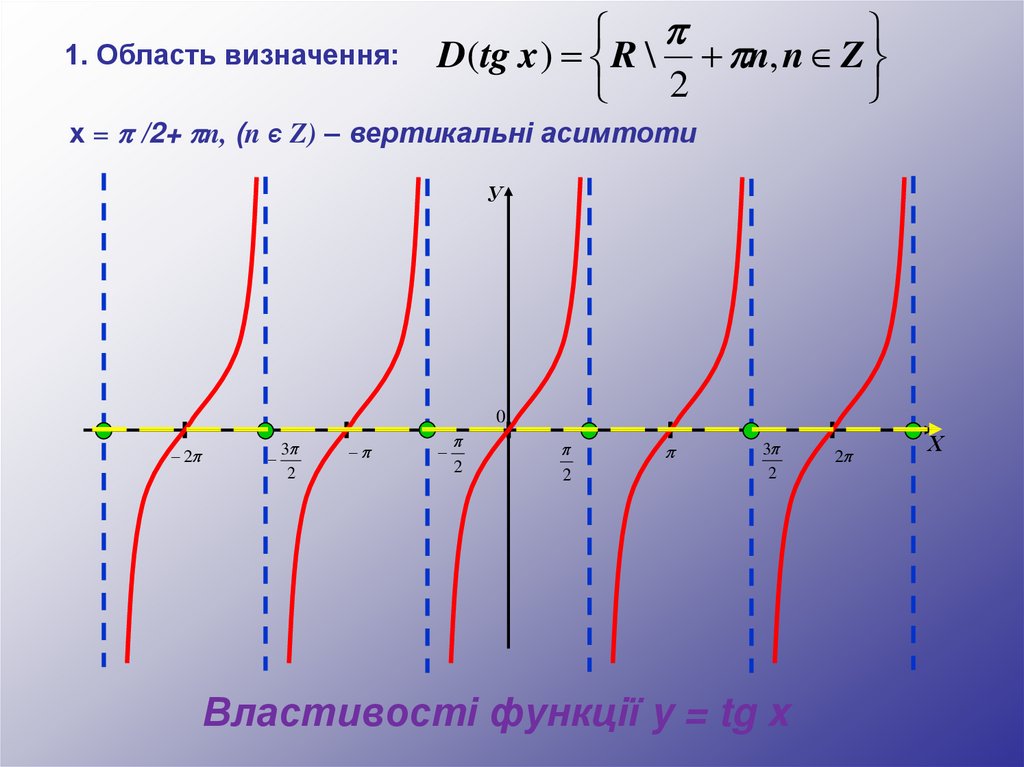
1. Область визначення:
D(tg x ) R \ + n, n Z
2
х = /2+ n, (n Є Z) – вертикальні асимтоти
У
0
2
3
2
2
2
3
2
Властивості функції y = tg x
2
Х

37. Властивості функції y = tg x

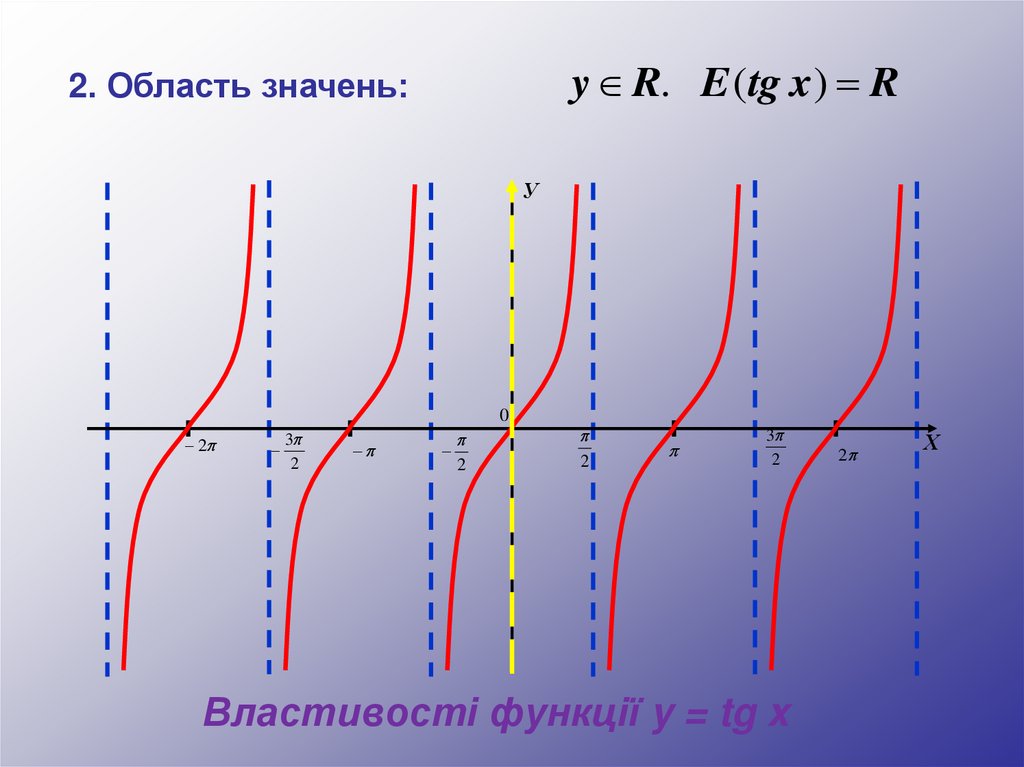
y R. E (tg x) R
2. Область значень:
У
0
2
3
2
2
2
3
2
Властивості функції y = tg x
2
Х

38. Властивості функції y = tg x

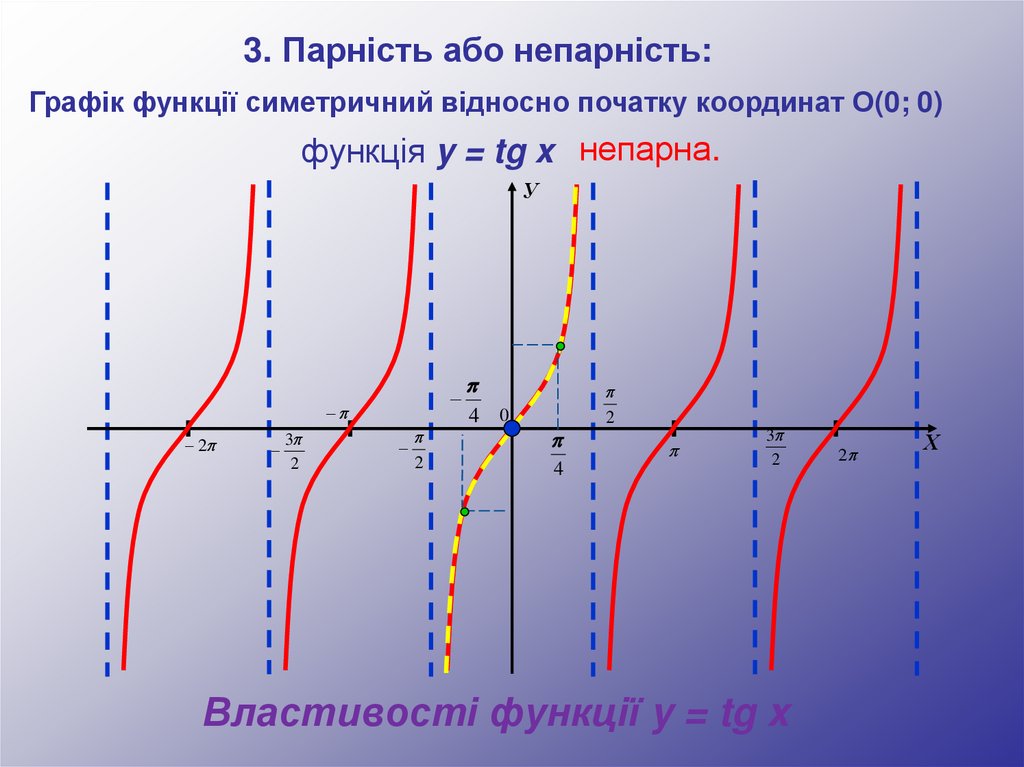
3. Парність або непарність:
Графік функції симетричний відносно початку координат О(0; 0)
функція y = tg x непарна.
У
2
3
2
2
4 0
4
2
3
2
Властивості функції y = tg x
2
Х

39. Властивості функції y = tg x

4. Періодичність: функція y = tg x періодична з періодом
T
Функція y = tg x – періодична з найменшим додатнім періодом T = .
tg (x + n) = tg x, (n Є Z)
У
0
2
3
2
2
2
Властивості функції y = tg x
3
2
2
Х

40.

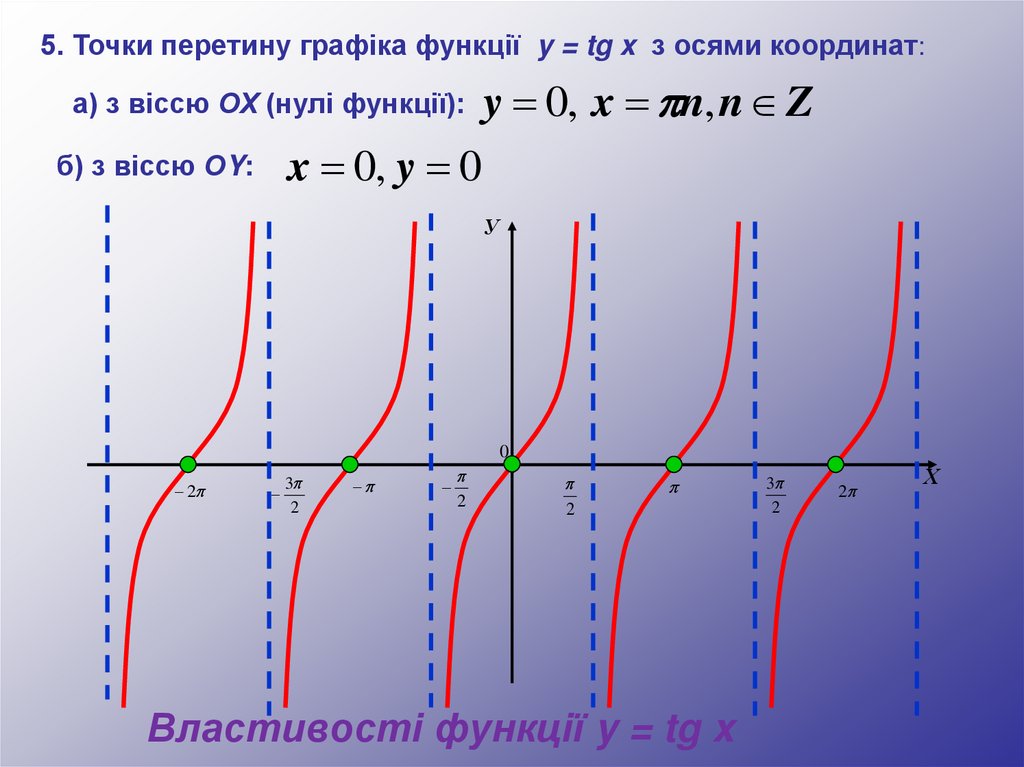
5. Точки перетину графіка функції y = tg x з осями координат:
а) з віссю ОХ (нулі функції):
y 0, x n, n Z
x 0, y 0
б) з віссю ОY:
У
0
2
3
2
2
2
Властивості функції y = tg x
3
2
2
Х

41.

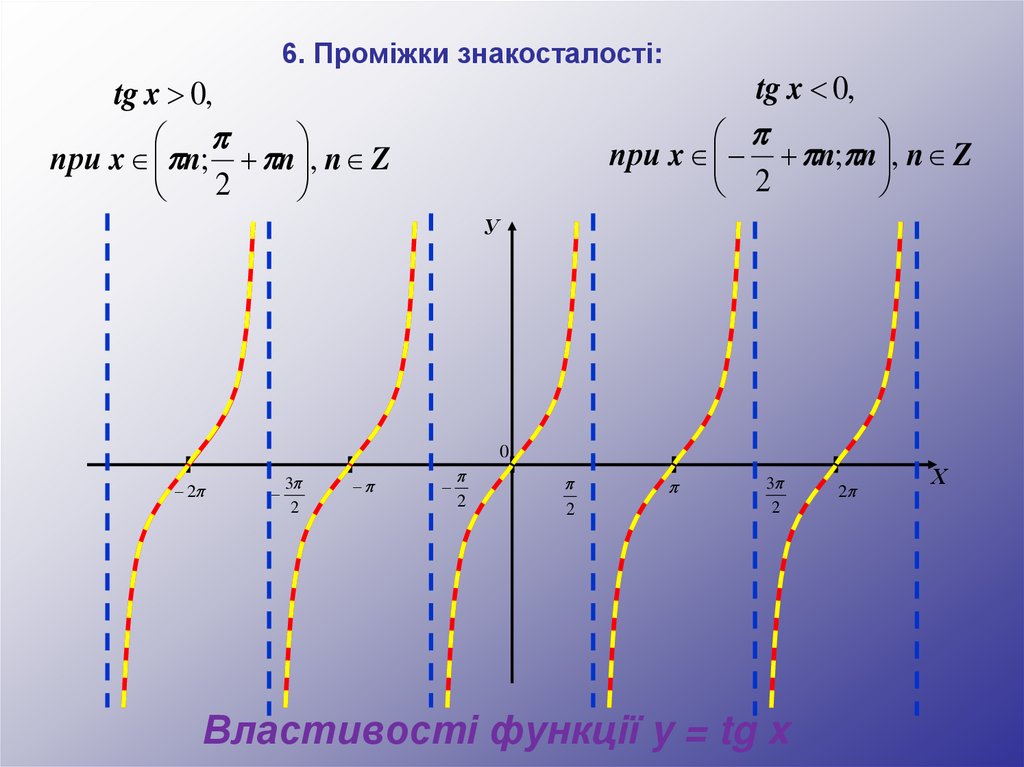
6. Проміжки знакосталості:
tg x 0,
при x + n; n , n Z
2
tg x 0,
при x n; + n , n Z
2
У
0
2
3
2
2
2
3
2
Властивості функції y = tg x
2
Х

42. Властивості функції y = tg x

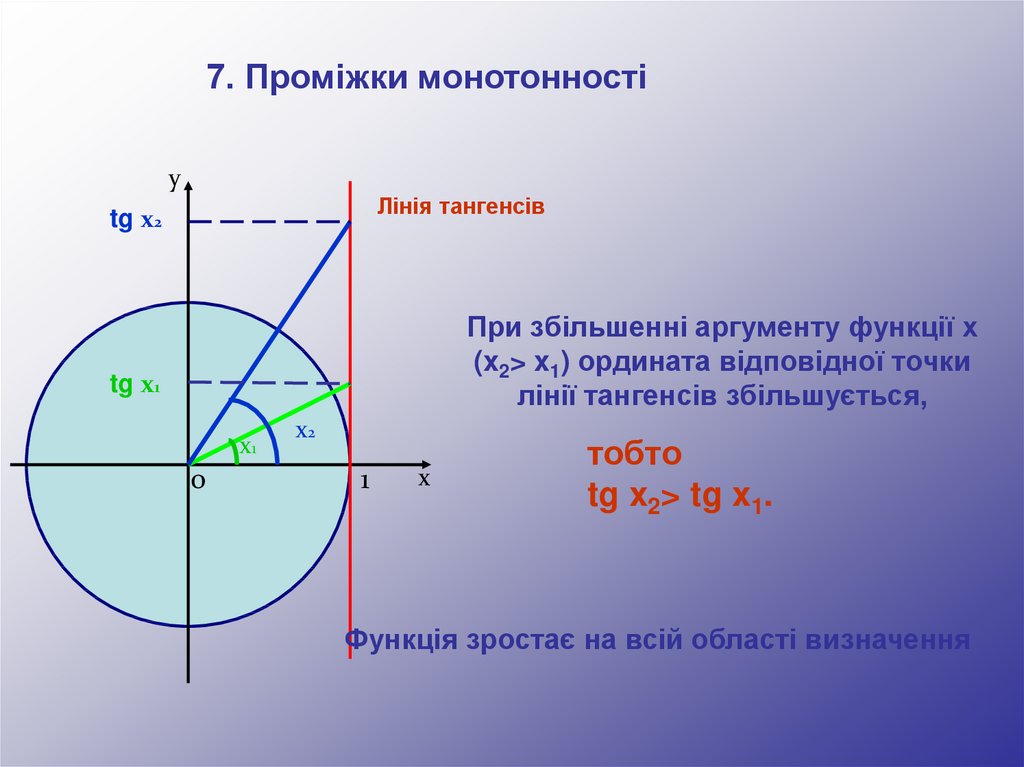
7. Проміжки монотонності
у
Лінія тангенсів
tg x2
При збільшенні аргументу функції х
(x2> x1) ордината відповідної точки
лінії тангенсів збільшується,
tg x1
x1
0
x2
1
х
тобто
tg x2> tg x1.
Функція зростає на всій області визначення

43. При збільшенні аргументу функції х (x2> x1) ордината відповідної точки лінії тангенсів збільшується,

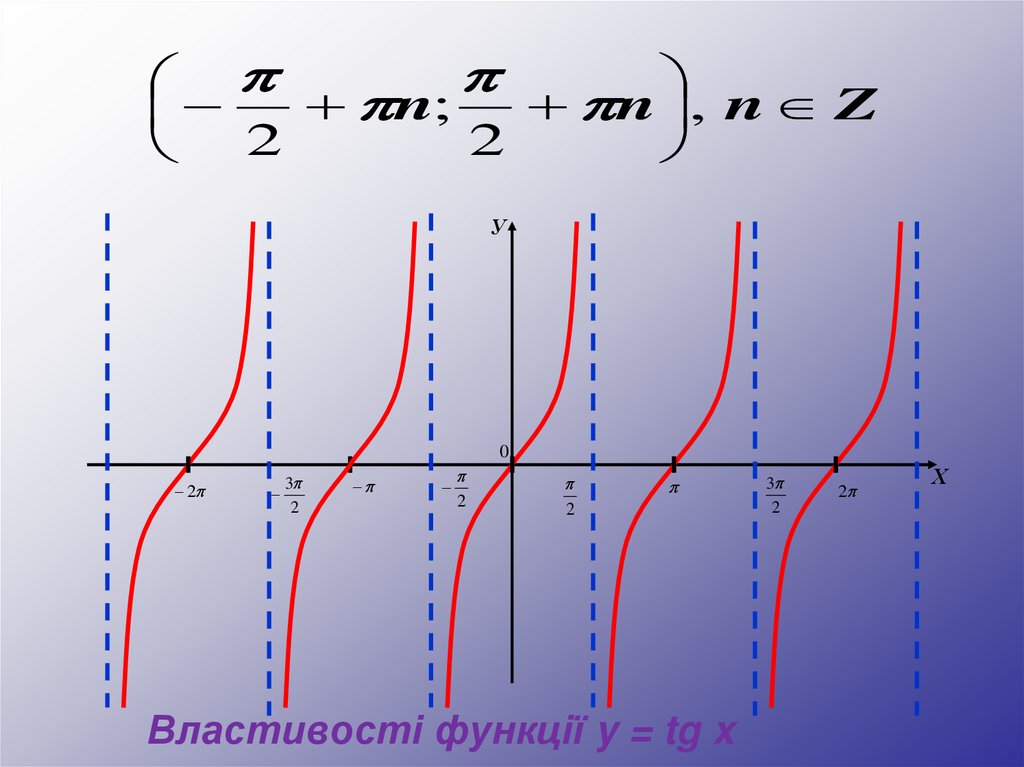
+ n;
+ n , n Z
2
2
У
0
2
3
2
2
2
Властивості функції y = tg x
3
2
2
Х

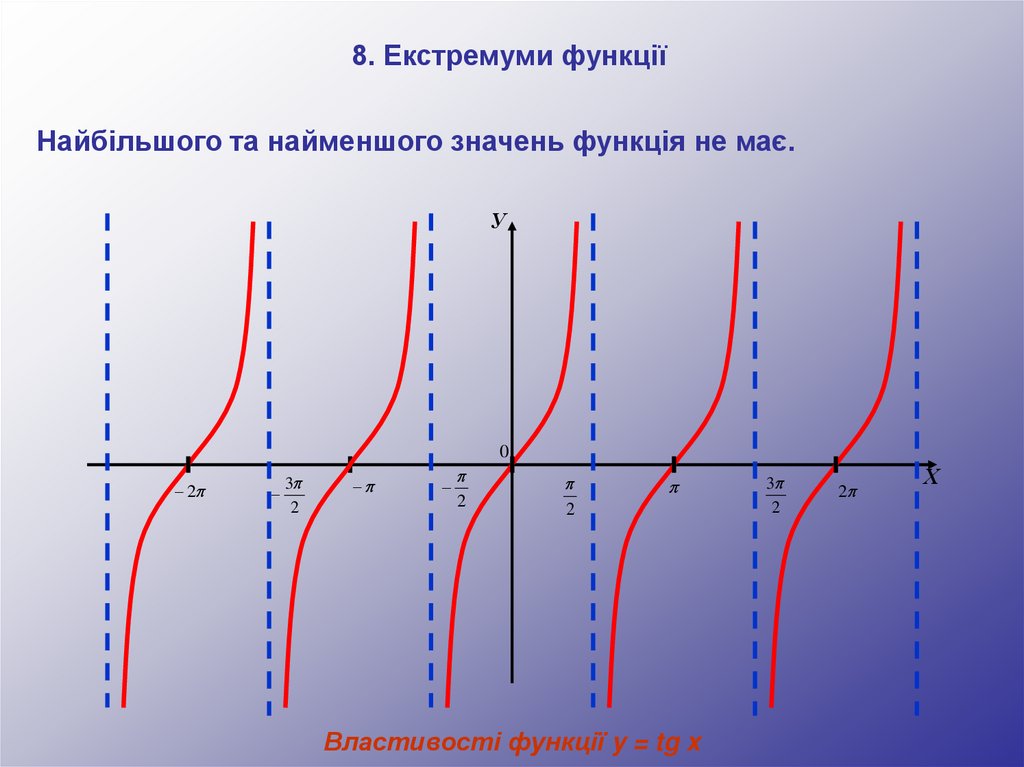
44.

8. Екстремуми функції
Найбільшого та найменшого значень функція не має.
У
0
2
3
2
2
2
Властивості функції y = tg x
3
2
2
Х

45. Властивості функції y = tg x

46. Виконання вправ на закріплення властивостей функції у= tg x

Побудувати графік функції y = - tg x
Для побудови графіка функції y = - tg x необхідно графік
функції y = tg x відобразити симетрично відносно осі OX.
У
0
2
3
2
2
2
3
2
2
Х

47. Перевір правильність виконання та запис пояснень до вправ:

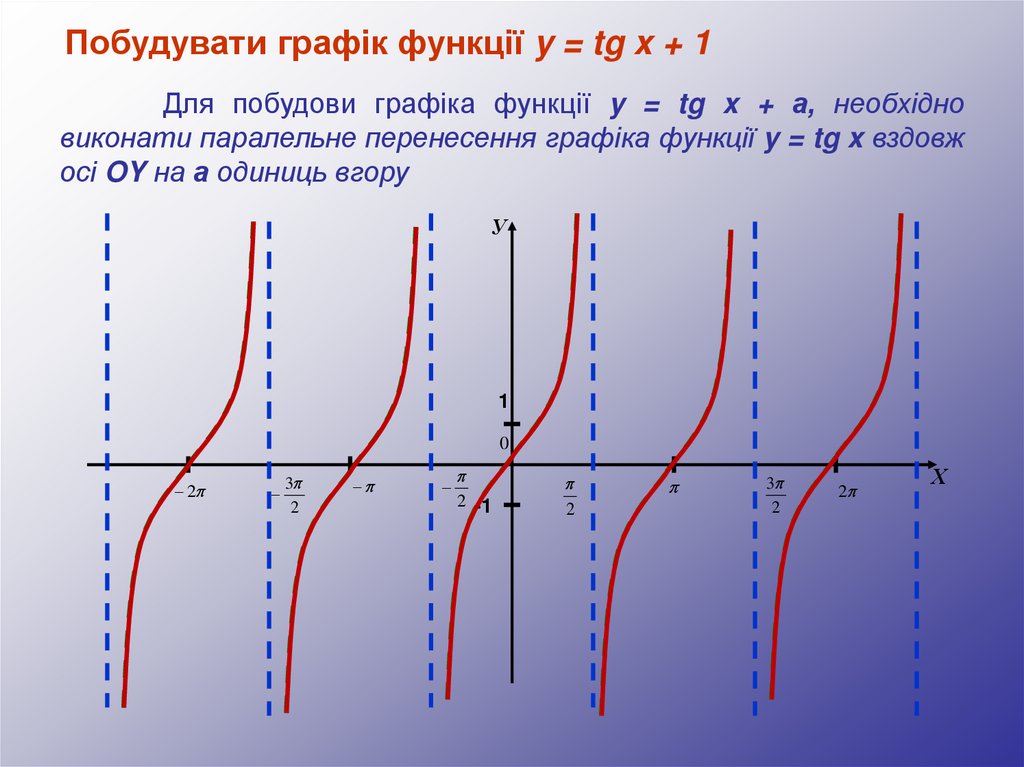
Побудувати графік функції y = tg x + 1
Для побудови графіка функції y = tg x + а, необхідно
виконати паралельне перенесення графіка функції y = tg x вздовж
осі OY на а одиниць вгору
У
1
0
2
3
2
2 -1
2
3
2
2
Х

48. Виконай самостійно:

Побудувати графік функції y = tg (x + /6)
Для побудови графіка функції y = tg (x + а), необхідно
виконати паралельне перенесення графіка функції y = tg x вздовж
осі OX на а одиниць вліво.
У
2
3
2
2
60
2
3
2
2
Х

49.

Побудувати графік функції y = Іtg xІ
Для побудови графіка функції y = | tg x |необхідно додатну
частину графіка функції y = tg x залишити незмінною, а від'ємну частину
відобразити симетрично відносно осі OX.
У
0
2
3
2
2
2
3
2
2
Х

50.

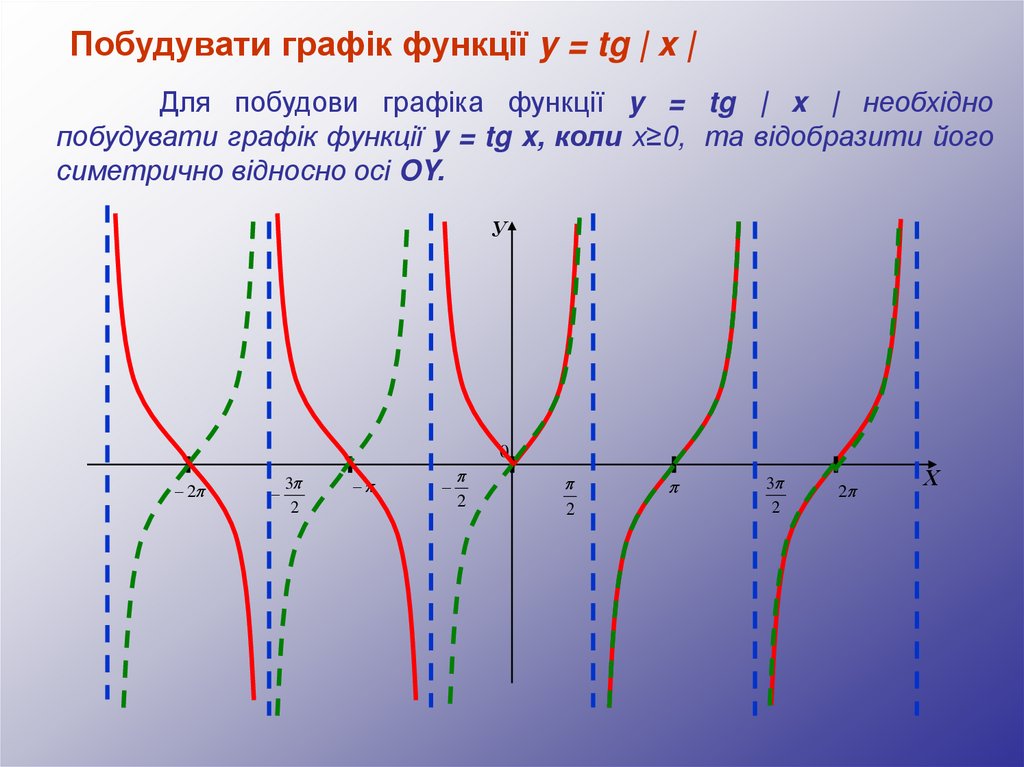
Побудувати графік функції y = tg | x |
Для побудови графіка функції y = tg | x | необхідно
побудувати графік функції y = tg x, коли x≥0, та відобразити його
симетрично відносно осі OY.
У
0
2
3
2
2
2
3
2
2
Х

51.

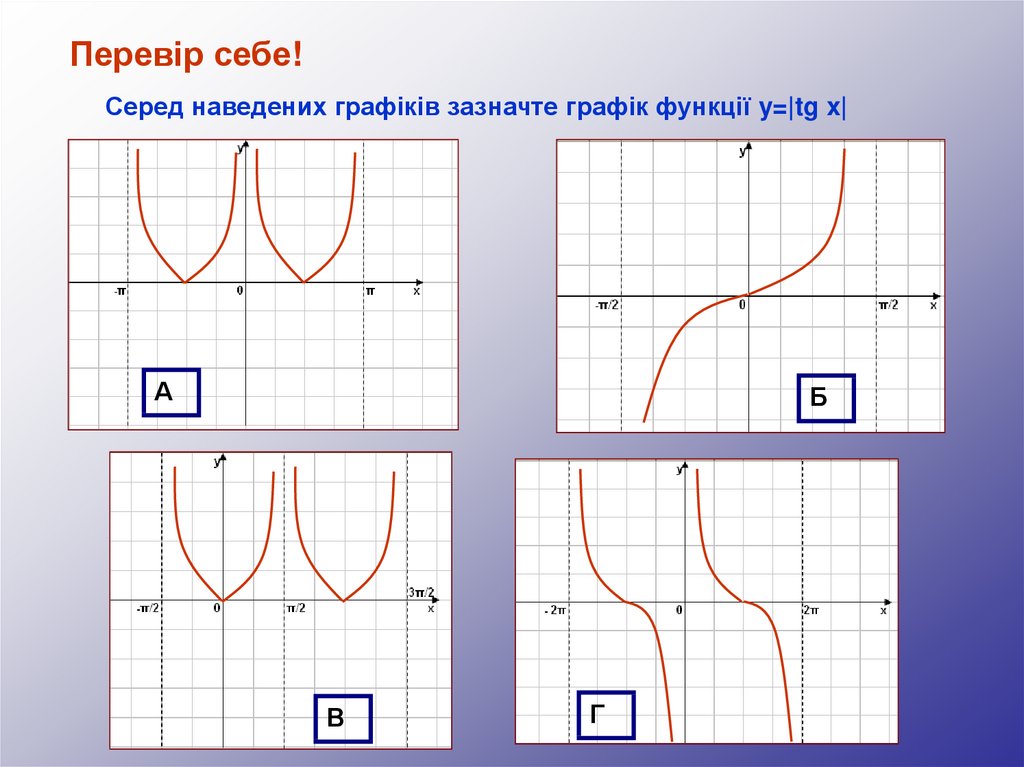
Перевір себе!
Серед наведених графіків зазначте графік функції y=|tg x|
А
Б
В
Г

52.

Перевір себе!
1. Функція y=2tg x зростає на проміжку:
А.
В.
+
n
;
+
n
,n Z
2
2
;+
Б.
n; + n , n Z
Г.
+
n
;
+ n , n Z
2
2
Д. + 2 n; + 2 n , n Z
2
2
2. Графік функція y = tgx паралельно перенесли на 2
одиниці вниз вздовж осі Oy і на π/4 одиниці вліво вздовж осі
Ox. Отримали наступний графік функції:
А.
y tg(x +
π
)- 2
4
Б.
В.
y 2tg(x
π
)
4
Г.
y tg(x
π
)- 2
4
y tg(2x -
π
)
4

53.

54.

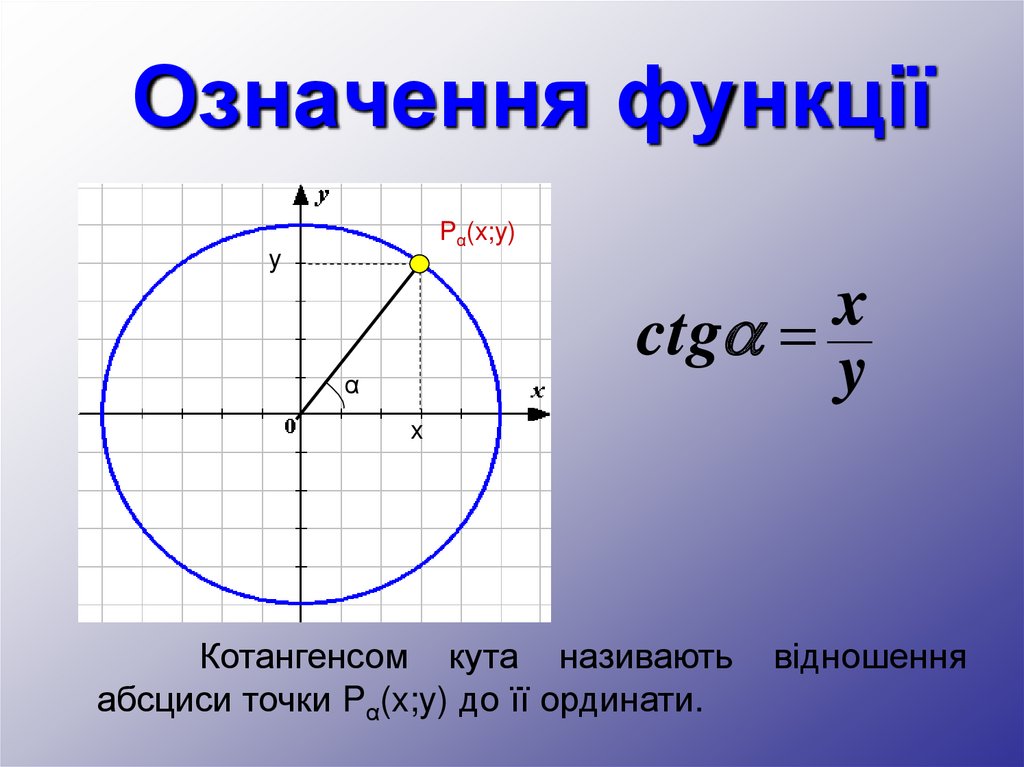
Означення функції
Pα(x;y)
y
x
ctg
y
α
x
Котангенсом кута називають
абсциси точки Pα(x;y) до її ординати.
відношення

55.

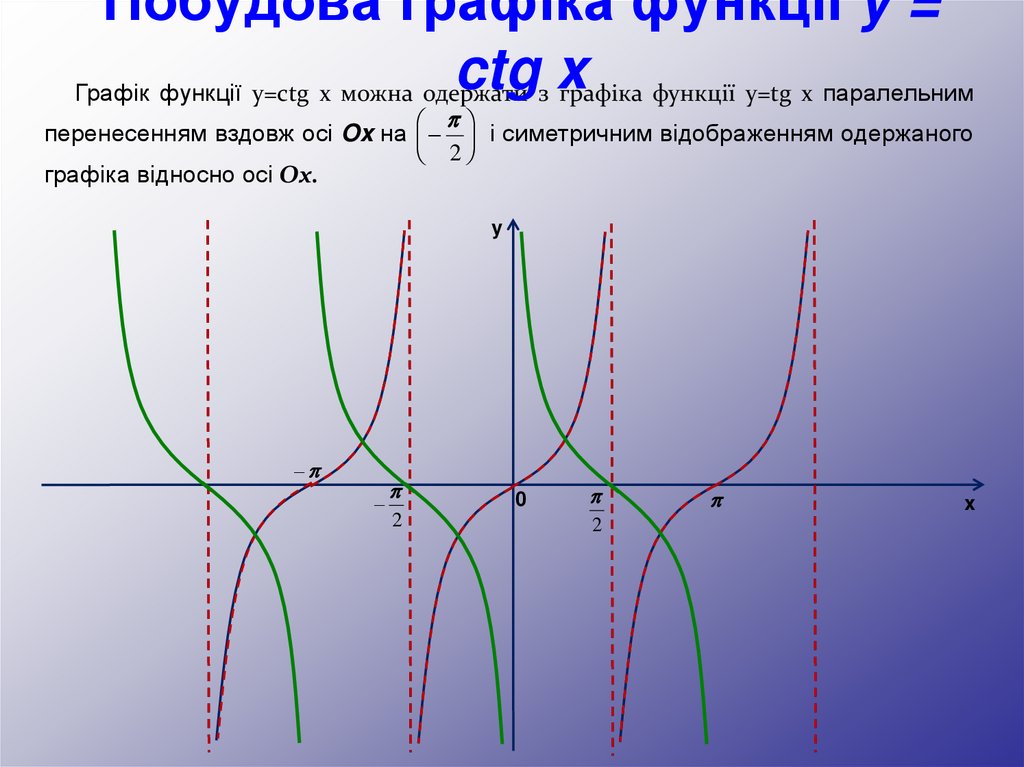
Побудова графіка функції y =
ctg x
Графік функції y=ctg x можна одержати з графіка функції y=tg x паралельним
перенесенням вздовж осі Ox на і симетричним відображенням одержаного
2
графіка відносно осі Ox.
y
2
0
2
x

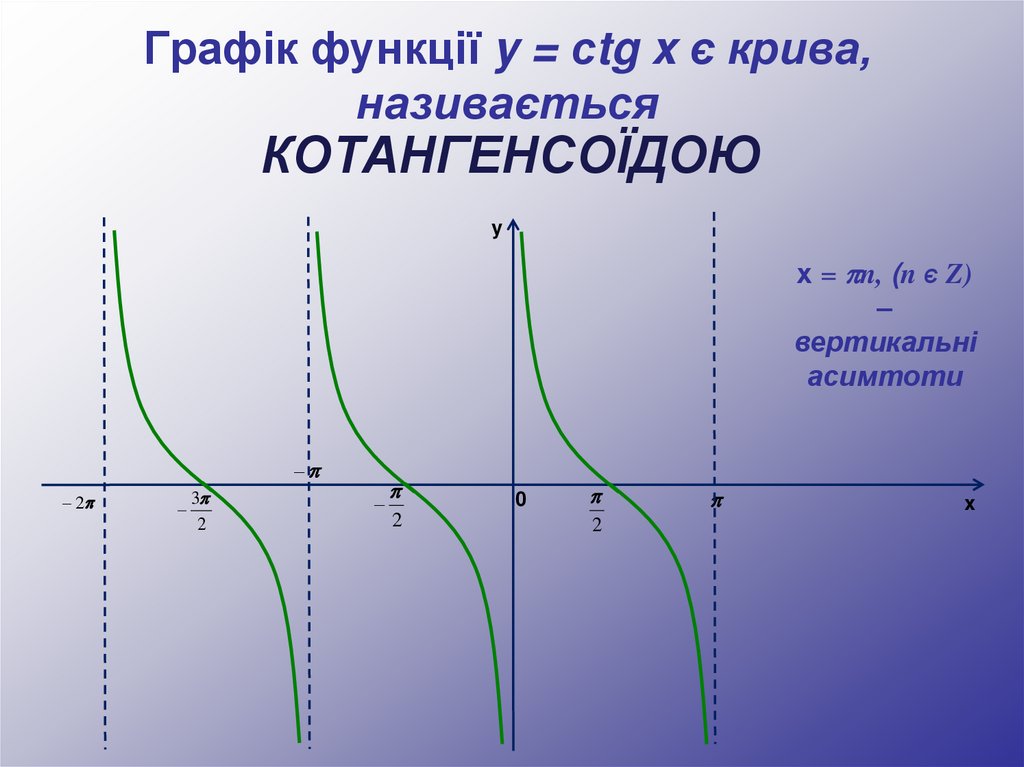
56.

Графік функції y = сtg x є крива,
називається
КОТАНГЕНСОЇДОЮ
y
х = n, (n Є Z)
–
вертикальні
асимтоти
2
3
2
2
0
2
x

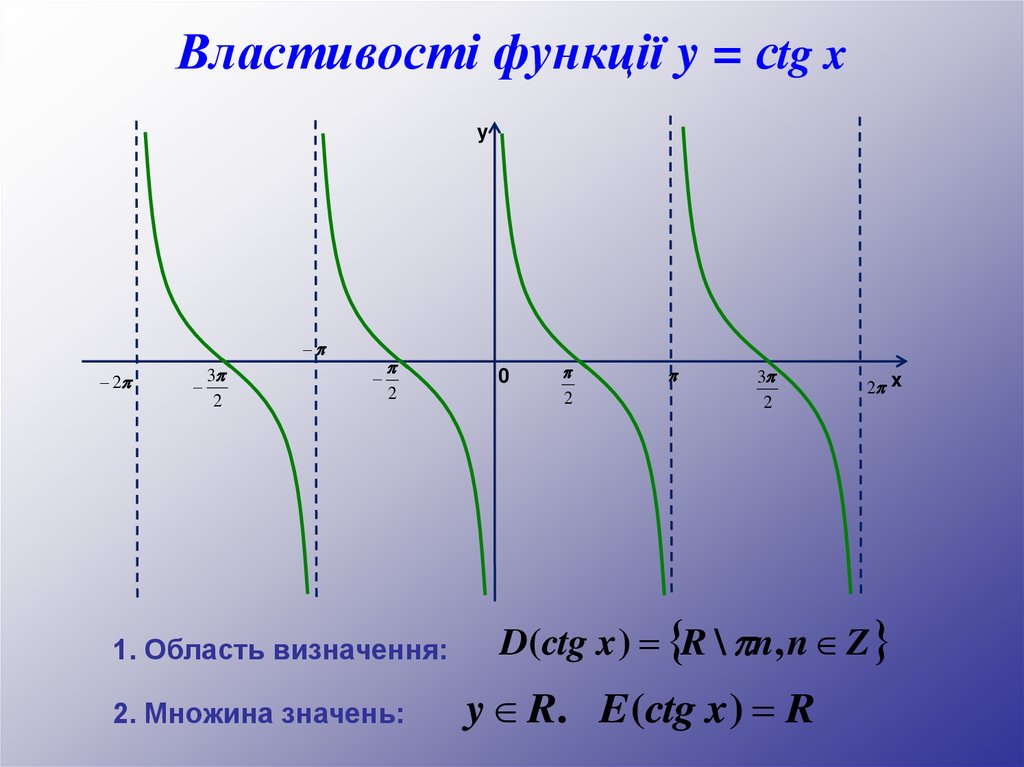
57.

Властивості функції y = сtg x
y
2
3
2
2
1. Область визначення:
2. Множина значень:
0
2
3
2
2 x
D(ctg x ) R \ n, n Z
y R. E (ctg x ) R

58. Означення функції

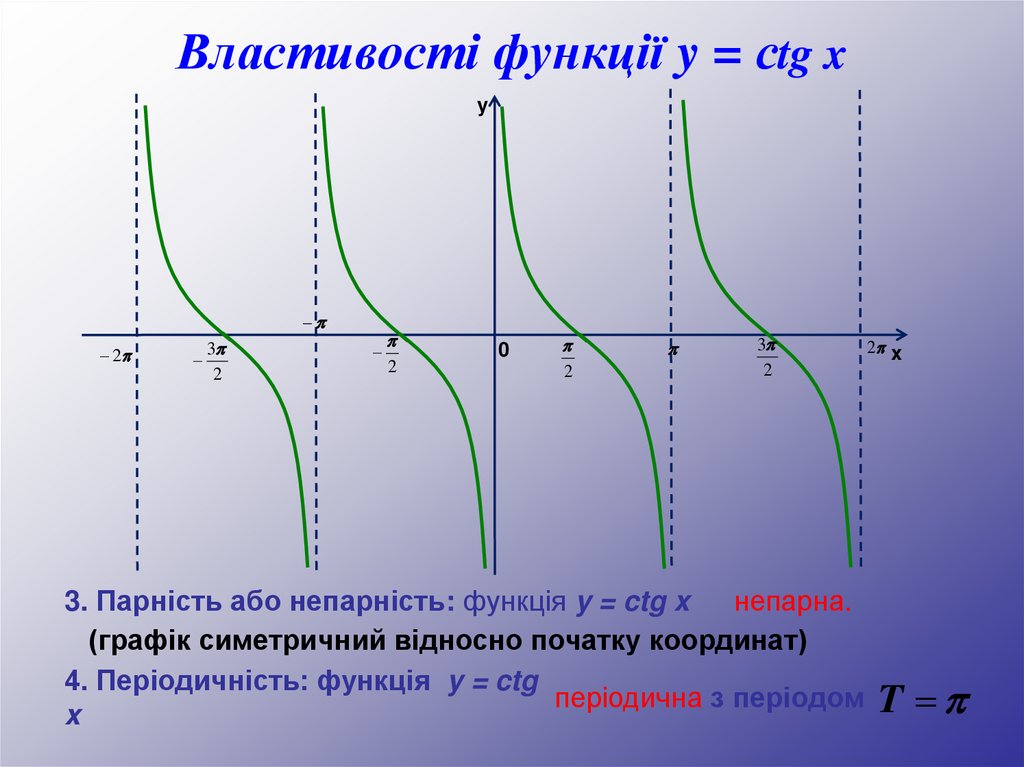
Властивості функції y = сtg x
y
2
3
2
2
0
2
3
2
3. Парність або непарність: функція y = ctg x
непарна.
(графік симетричний відносно початку координат)
4. Періодичність: функція y = ctg
періодична з періодом
x
2 x
T

59. Побудова графіка функції y = ctg x

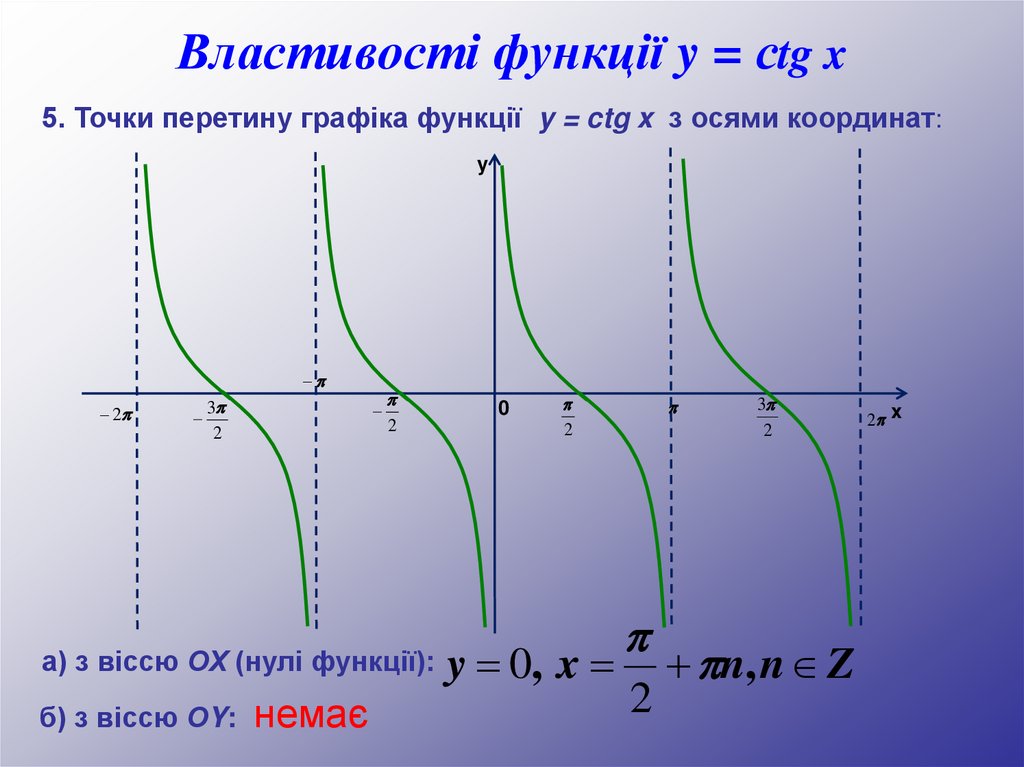
Властивості функції y = сtg x
5. Точки перетину графіка функції y = ctg x з осями координат:
y
2
3
2
2
а) з віссю ОХ (нулі функції):
б) з віссю ОY:
немає
0
2
y 0, x
2
3
2
+ n, n Z
2 x

60. Графік функції y = сtg x є крива, називається

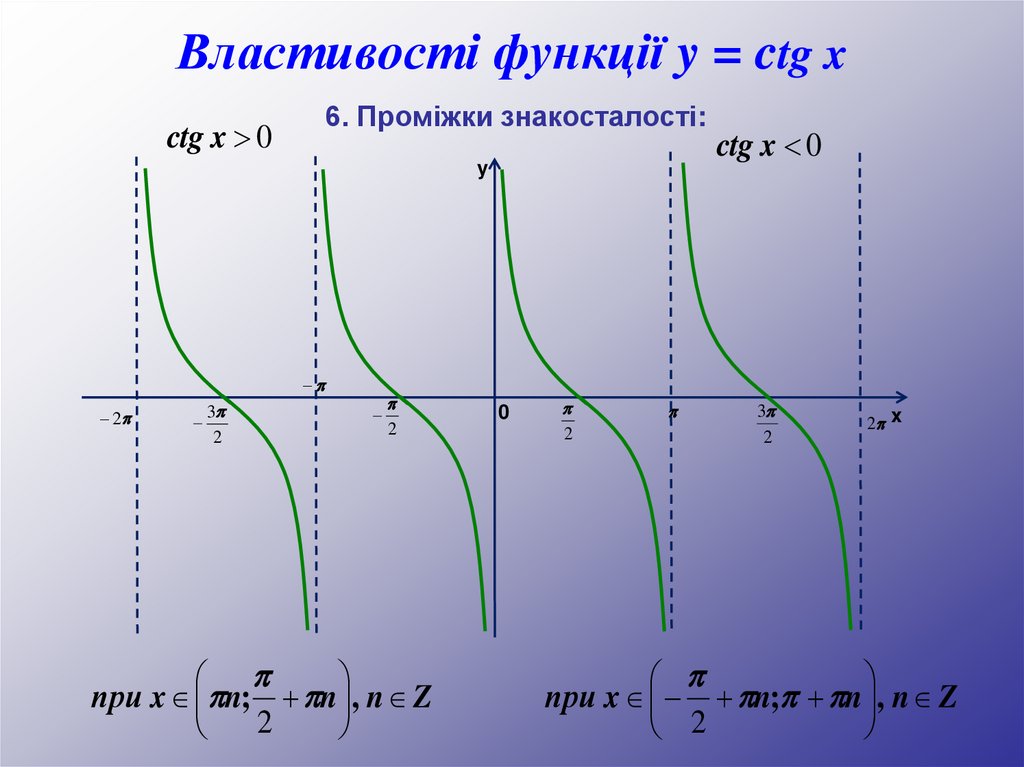
Властивості функції y = ctg x
6. Проміжки знакосталості:
ctg x 0
y
2
3
2
2
при x n; + n , n Z
2
0
2
ctg x 0
3
2
2 x
при x + n; + n , n Z
2

61. Властивості функції y = сtg x

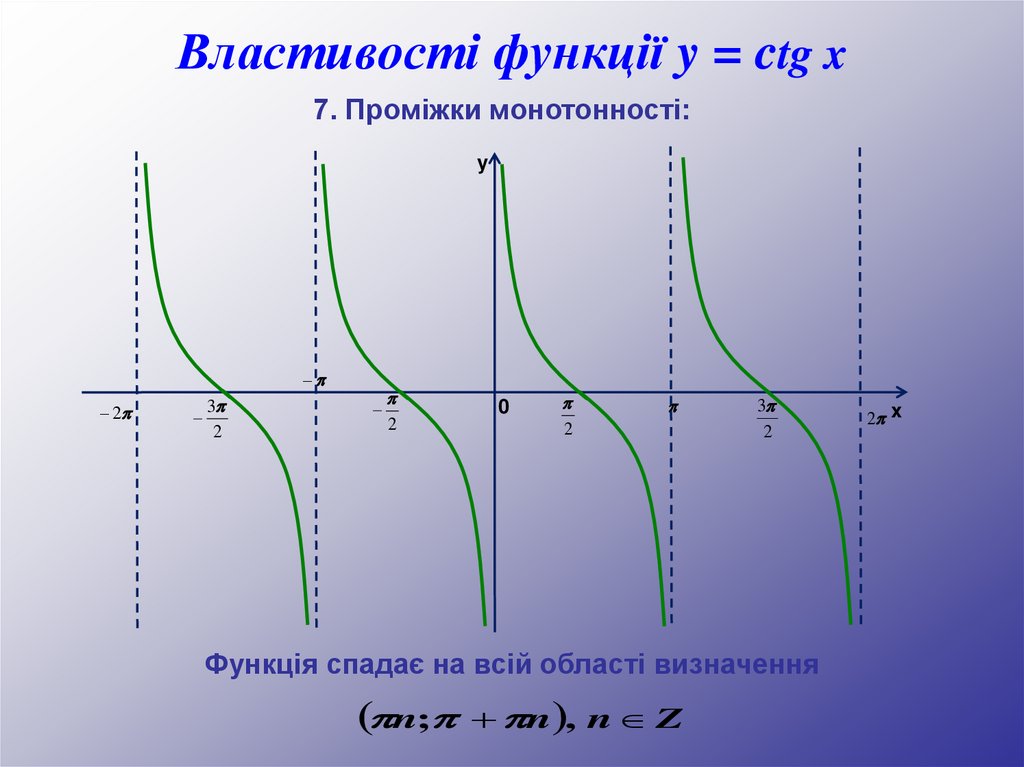
Властивості функції y = ctg x
7. Проміжки монотонності:
y
2
3
2
2
0
2
3
2
Функція спадає на всій області визначення
n;
+ n , n Z
2 x

62. Властивості функції y = сtg x

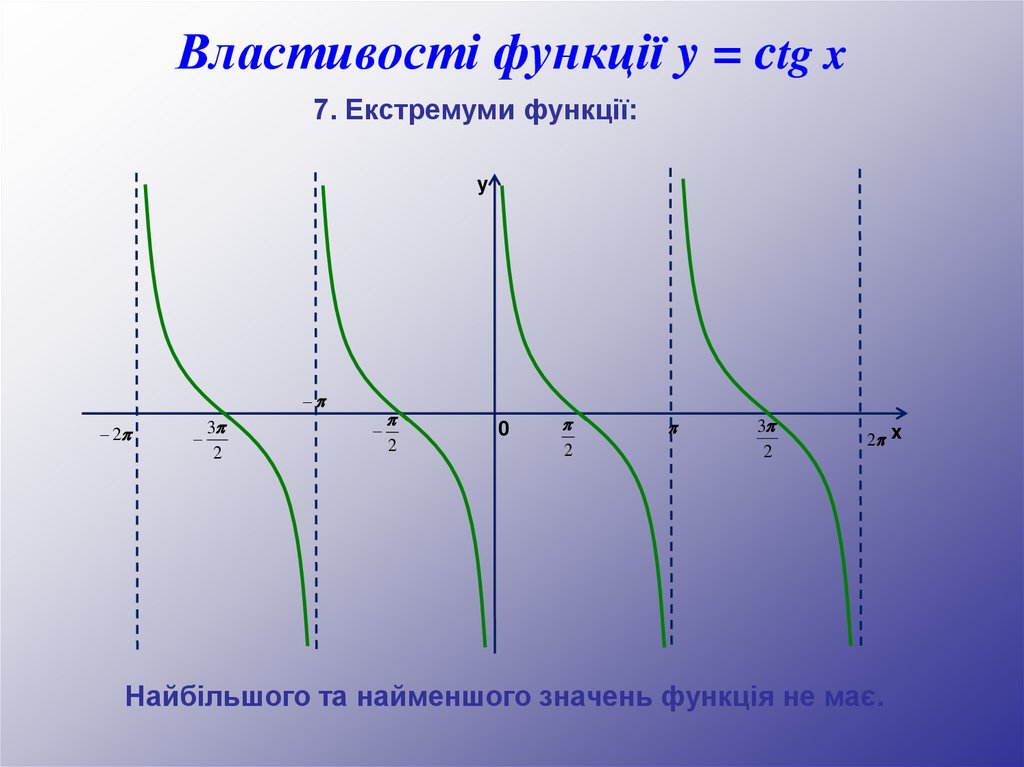
Властивості функції y = ctg x
7. Екстремуми функції:
y
2
3
2
2
0
2
3
2
2 x
Найбільшого та найменшого значень функція не має.

63. Властивості функції y = сtg x

64. Властивості функції y = ctg x

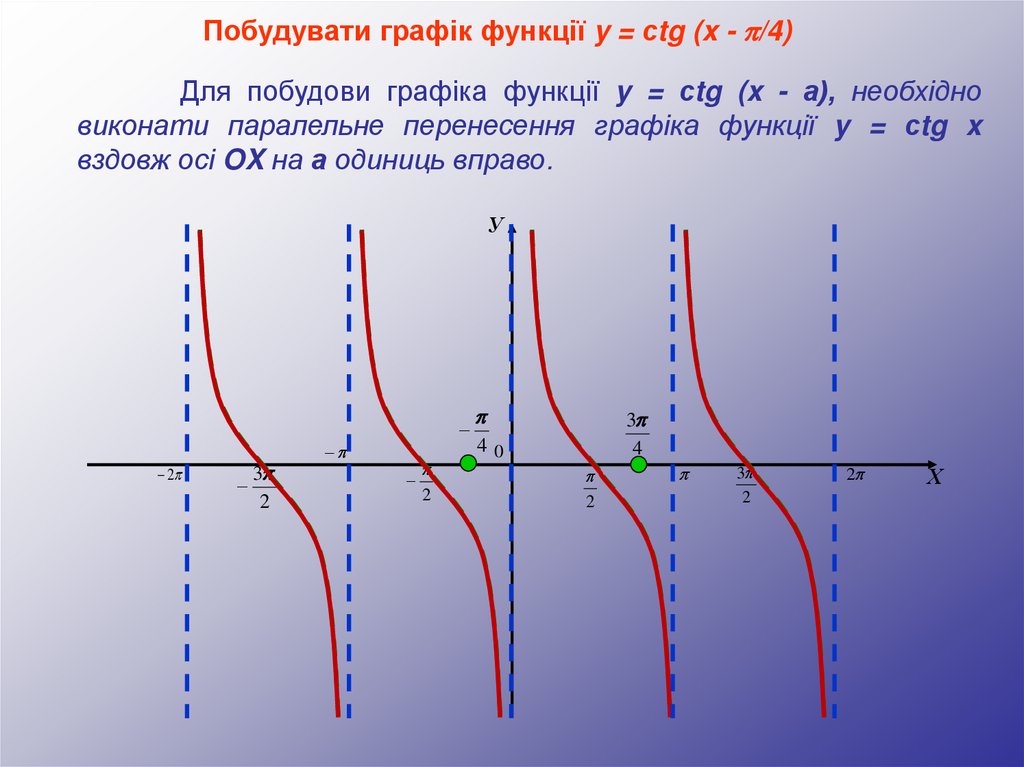
Побудувати графік функції y = сtg (x - /4)
Для побудови графіка функції y = сtg (x - а), необхідно
виконати паралельне перенесення графіка функції y = сtg x
вздовж осі OX на а одиниць вправо.
У
2
3
2
2
3
4
40
2
3
2
2
Х

65. Властивості функції y = ctg x

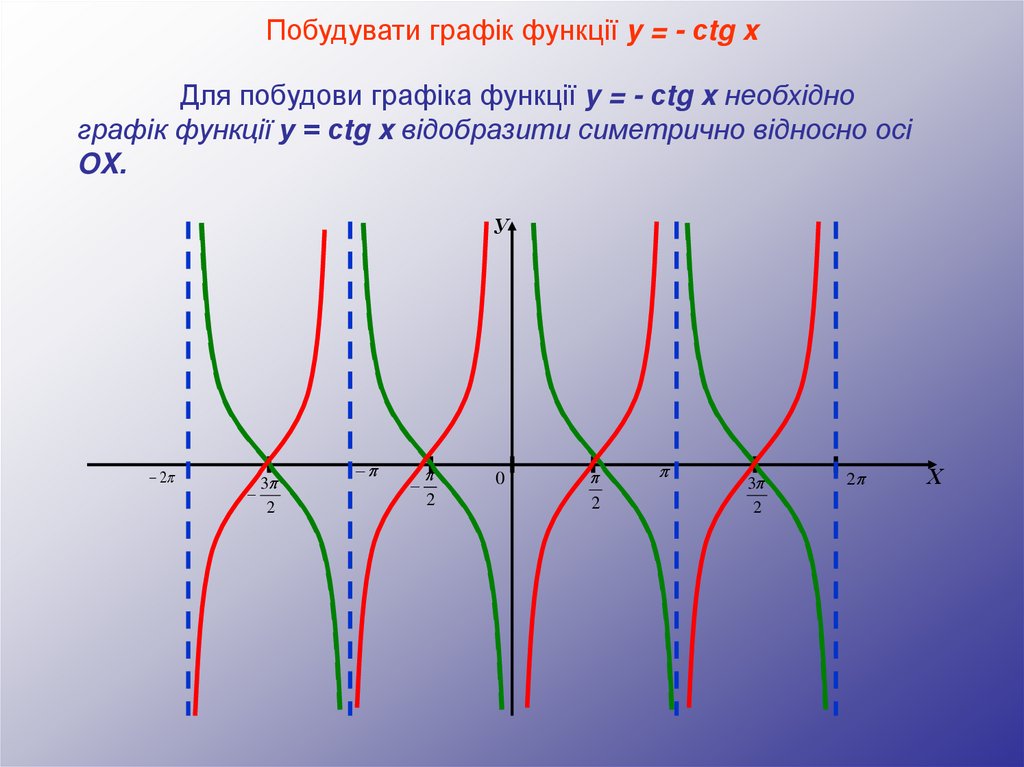
Побудувати графік функції y = - сtg x
Для побудови графіка функції y = - сtg x необхідно
графік функції y = сtg x відобразити симетрично відносно осі
OX.
У
2
3
2
2
0
2
3
2
2
Х

66. Властивості функції y = ctg x

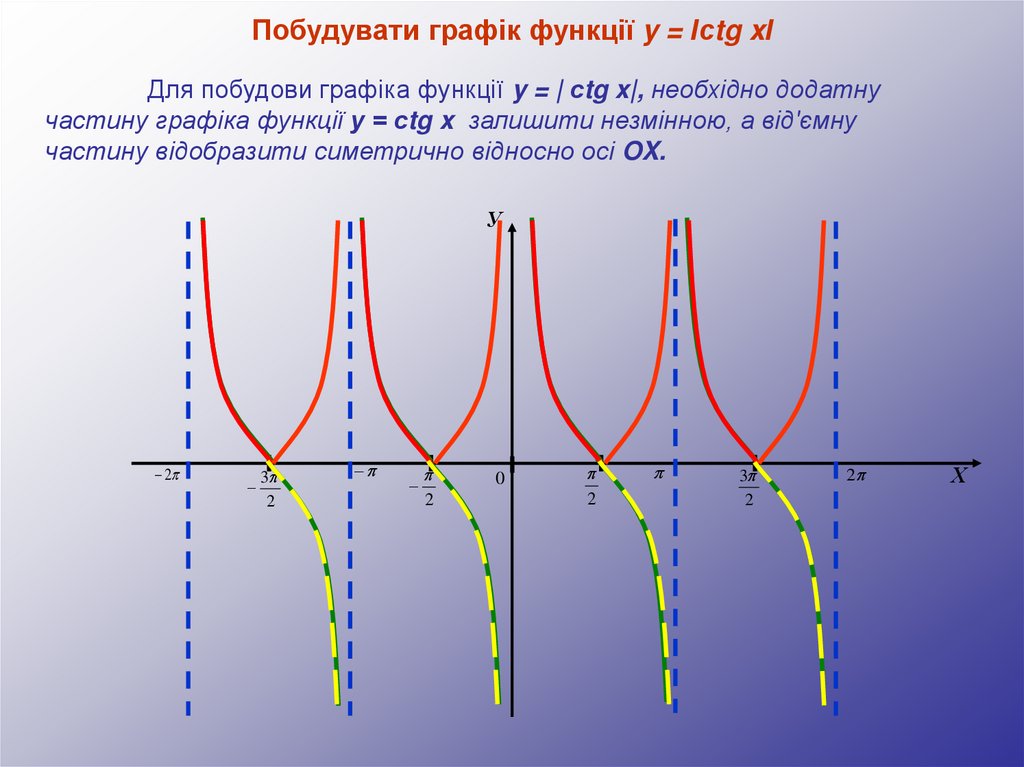
Побудувати графік функції y = Ісtg xІ
Для побудови графіка функції y = | сtg x|, необхідно додатну
частину графіка функції y = сtg x залишити незмінною, а від'ємну
частину відобразити симетрично відносно осі OX.
У
2
3
2
2
0
2
3
2
2
Х

67.

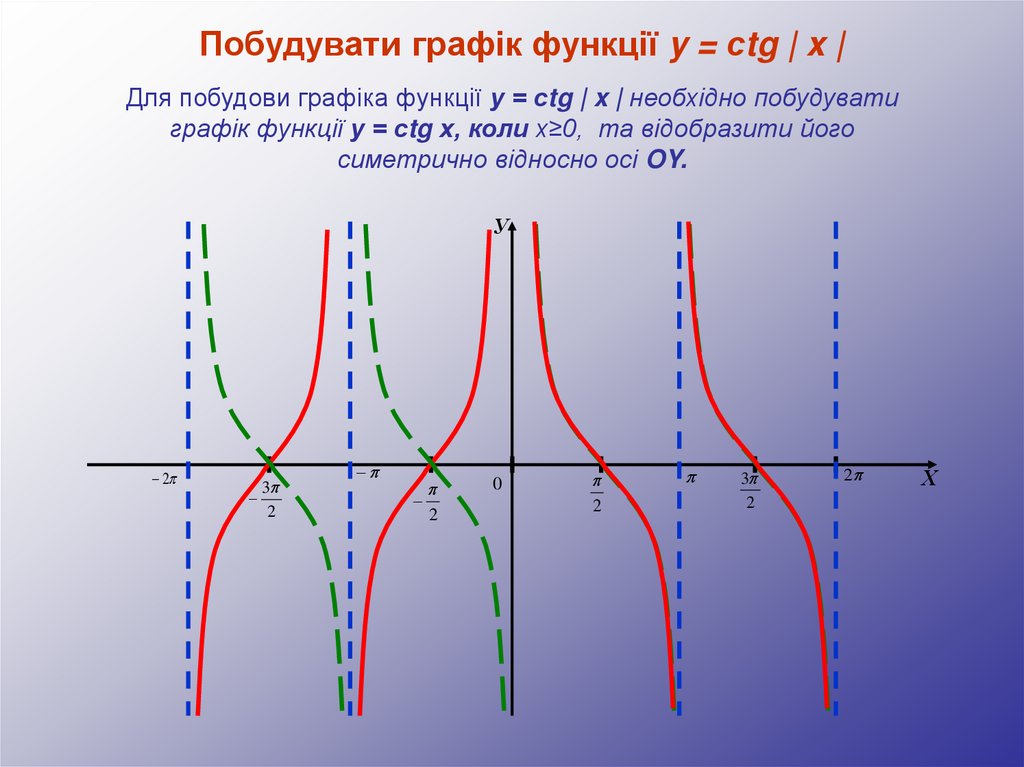
Побудувати графік функції y = сtg | x |
Для побудови графіка функції y = сtg | x | необхідно побудувати
графік функції y = сtg x, коли x≥0, та відобразити його
симетрично відносно осі OY.
У
2
3
2
2
0
2
3
2
2
Х

68.

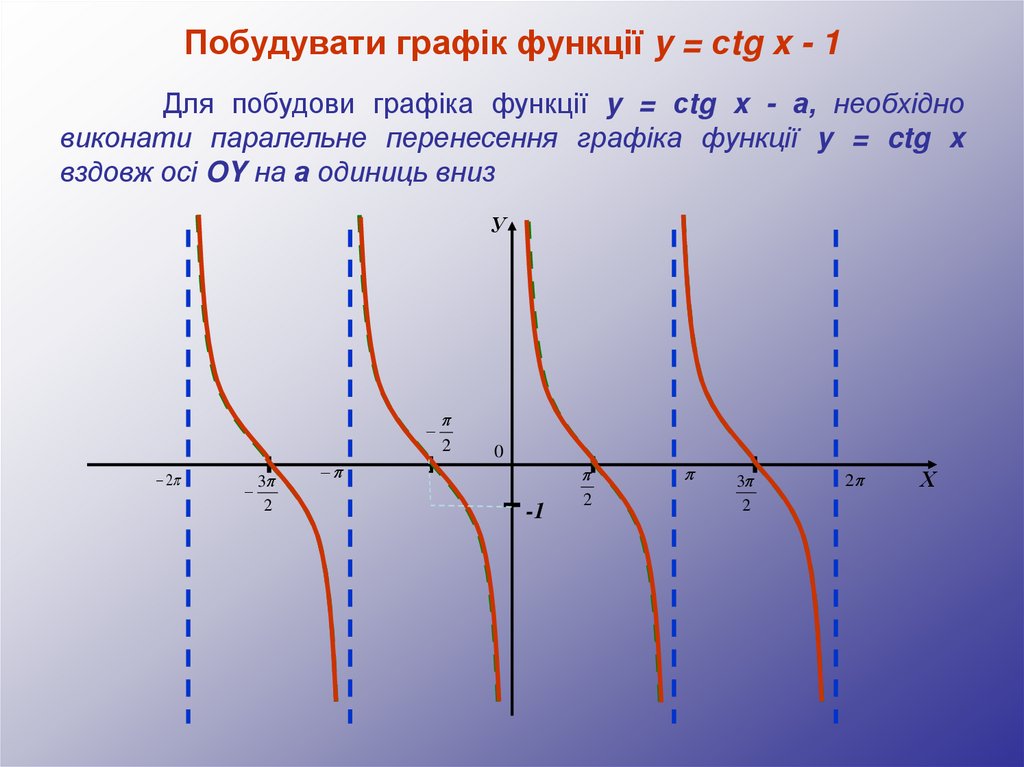
Побудувати графік функції y = сtg x - 1
Для побудови графіка функції y = сtg x - а, необхідно
виконати паралельне перенесення графіка функції y = ctg x
вздовж осі OY на а одиниць вниз
У
2
3
2
2
0
-1
2
3
2
2
Х