Similar presentations:
Перетворення графіків функцій
1. Перетворення графіків функцій
Алгебра, 9 клас2. У презентації розглянемо:
3.
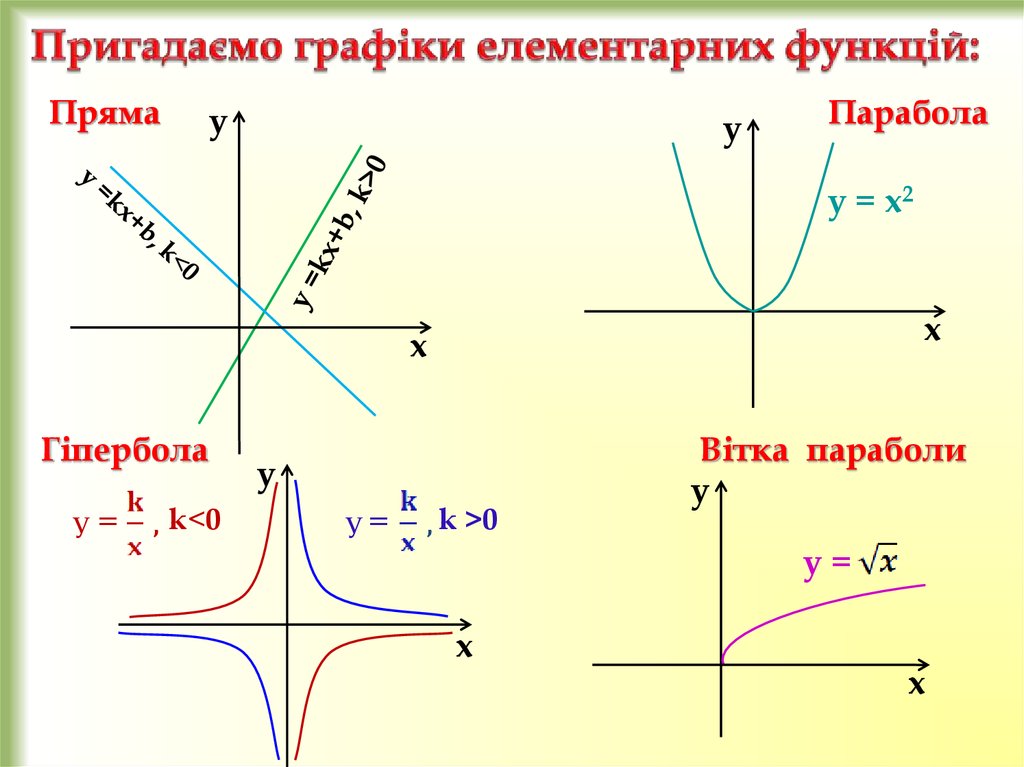
Прямау
у
Парабола
у = х2
х
х
Гіпербола
У
=
, k<0
у
У=
, k >0
Вітка параболи
у
у=
х
х
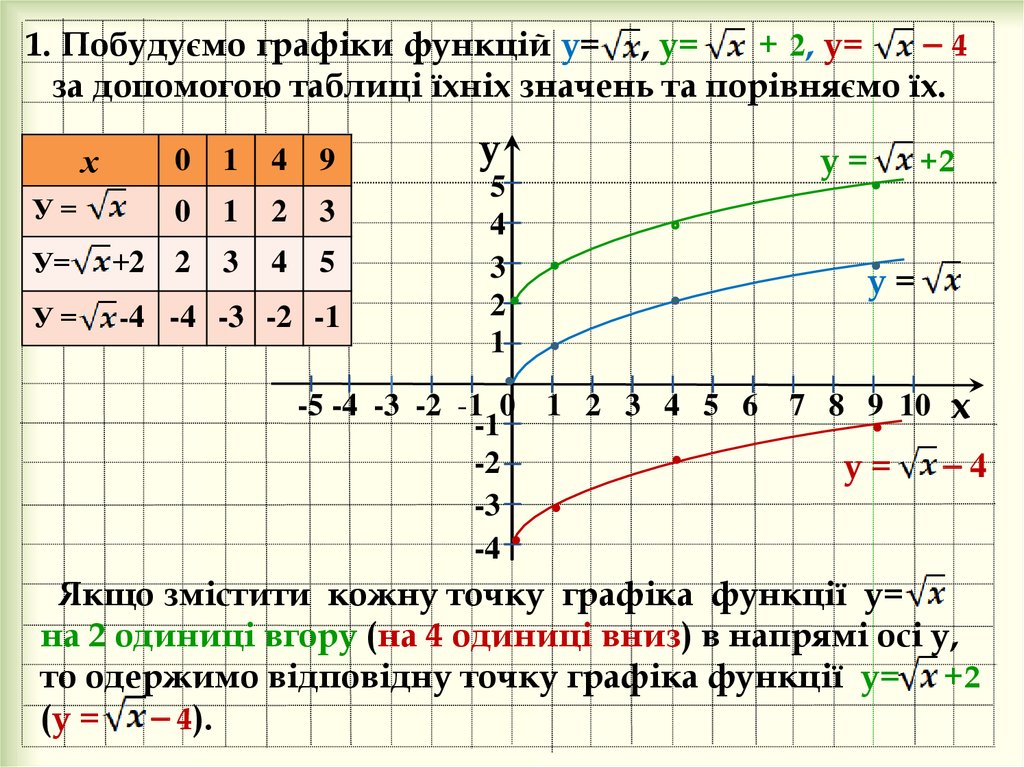
4. 1. Побудуємо графіки функцій у= , у= + 2, у= ⎯ 4 за допомогою таблиці їхніх значень та порівняємо їх.
1. Побудуємо графіки функцій у= , у=+ 2, у=
⎯4
за допомогою таблиці їхніх значень та порівняємо їх.
х
У=
0
1
4
9
0
1
2
3
2
3
4
5
У=
+2
У=
-4 -4 -3 -2 -1
y
у=
5
4
3
2
1
-5 -4 -3 -2 -1 0
-1
-2
-3
-4
+2
у=
1 2 3 4 5 6
7 8 9 10
x
у=
⎯4
Якщо змістити кожну точку графіка функції у=
на 2 одиниці вгору (на 4 одиниці вниз) в напрямі осі у,
то одержимо відповідну точку графіка функції у= +2
(у = ⎯ 4).
5. 1. Побудова графіка функції у = f(x) + n, де n ˃ 0. Графік функції y=f(x)+n, де n>0, можна одержати із графіка функції y=f(x)
1. Побудова графіка функції у = f(x) + n, де n ˃ 0.Графік функції y=f(x)+n, де n>0, можна одержати із
графіка функції y=f(x) за допомогою паралельного
перенесення вздовж осі у на n одиниць угору.
Графік функції y=f(x)⎯n, де n>0, можна одержати із
графіка функції y=f(x) за допомогою паралельного
перенесення вздовж осі у на n одиниць униз.
6.
Побудуємо графіки функцій у = х² + 1, у = х² ⎯ 3.І спосіб. Використаємо шаблон графіка функції у = х².
y
5
4
3
2
1
-5 -4 -3 -2 -1 0
-1
-2
-3
-4
у = х² + 1
у = х²
1 2 3 4 5 6
7 8 9 10
x
у = х² ⎯ 3
ІІ спосіб. Для побудови графіка функції у = х² + 1 піднімемо
вісь Ох вгору на 1 одиницю, для побудови графіка функції
у = х² ⎯ 3 опустимо вісь Ох вниз на 3 одиниці і побудуємо
графік функції у = х².
7.
Побудуйте графіки функцій у= х²⎯ 1, у= х²+ 2, у= х² ⎯ 5.y
у = х² + 2
5
4
3
2
1
у = х²⎯ 1
-5 -4 -3 -2 -1 0
-1
-2
-3
-4
-5
1 2 3 4 5 6
у = х² ⎯ 5
7 8 9 10
x
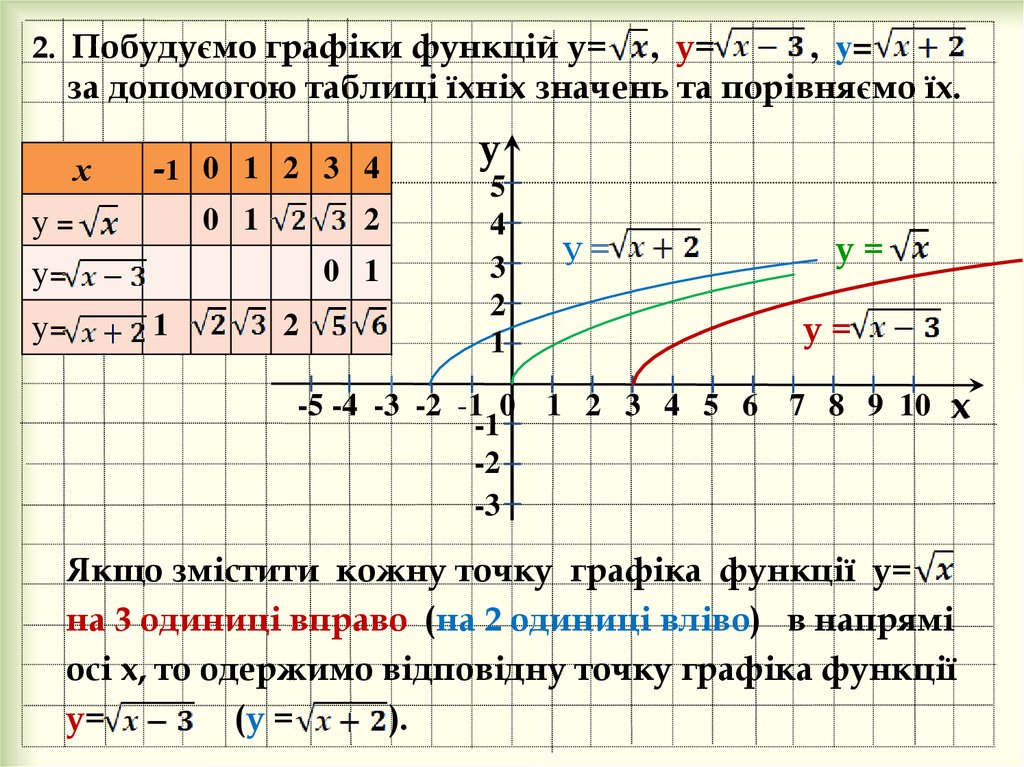
8. 2. Побудуємо графіки функцій у= , у= , у= за допомогою таблиці їхніх значень та порівняємо їх.
х-1 0 1 2 3 4
у=
0 1
2
у=
у=
0 1
1
2
y
5
4
3
2
1
-5 -4 -3 -2 -1 0
-1
-2
-3
У
=
у=
у=
1 2 3 4 5 6
7 8 9 10
x
Якщо змістити кожну точку графіка функції у=
на 3 одиниці вправо (на 2 одиниці вліво) в напрямі
осі х, то одержимо відповідну точку графіка функції
у=
(у =
).
9. 2. Побудова графіка функції у= f(x + m), де m ˃ 0. Графік функції y = f(x⎯m), де m > 0, можна одержати із графіка функції y=
2. Побудова графіка функції у= f(x + m), де m ˃ 0.Графік функції y = f(x⎯m), де m > 0, можна одержати
із графіка функції y= f(x) за допомогою паралельного
перенесення вздовж осі x на m одиниць праворуч.
Графік функції y = f(x+m), де m > 0, можна одержати
із графіка функції y= f(x) за допомогою паралельного
перенесення вздовж осі x на m одиниць ліворуч.
10.
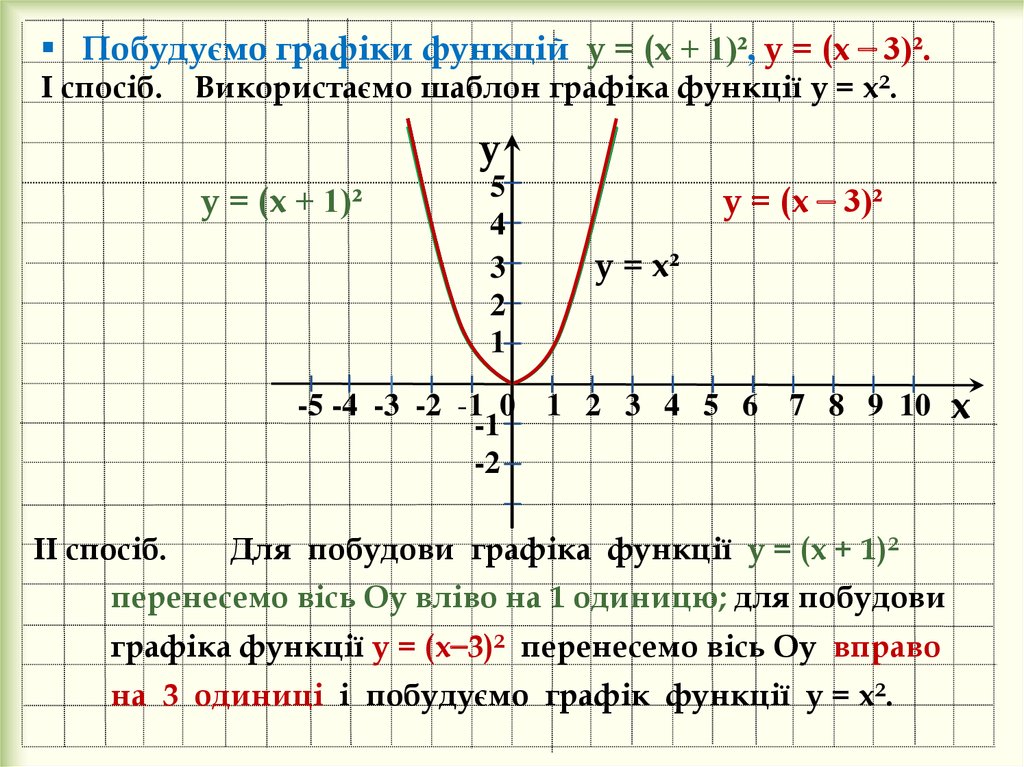
Побудуємо графіки функцій у = (х + 1)², у = (х ⎯ 3)².І спосіб.
Використаємо шаблон графіка функції у = х².
y
у = (х + 1)²
5
4
3
2
1
-5 -4 -3 -2 -1 0
-1
-2
ІІ спосіб.
у = (х ⎯ 3)²
у = х²
1 2 3 4 5 6
7 8 9 10
Для побудови графіка функції у = (х + 1)²
перенесемо вісь Оу вліво на 1 одиницю; для побудови
графіка функції у = (х⎯3)² перенесемо вісь Оу вправо
на 3 одиниці і побудуємо графік функції у = х².
x
11.
Побудуйте графіки функцій у=(х⎯ 1)², у=(х+ 2)², у=(х⎯5)².y
у = (х + 2)²
5
4
3
2
1
-5 -4 -3 -2 -1 0
-1
-2
-3
-4
-5
у = (х⎯ 1)²
у = (х ⎯ 5)²
1 2 3 4 5 6
7 8 9 10
x
12. 3. Побудова графіка функції y= f(x ± m) ± n, де m > 0 і n > 0. Графік функції y= f(x ± m) ± n, де m > 0 і n > 0, можна одержати
3. Побудова графіка функції y= f(x ± m) ± n, деm > 0 і n > 0.
Графік функції y= f(x ± m) ± n, де m > 0 і n > 0,
можна одержати із графіка функції y= f(x) за
допомогою паралельного перенесення вздовж
осі x на m одиниць ліворуч (праворуч), а потім
уздовж осі у на n одиниць вгору (вниз).
13.
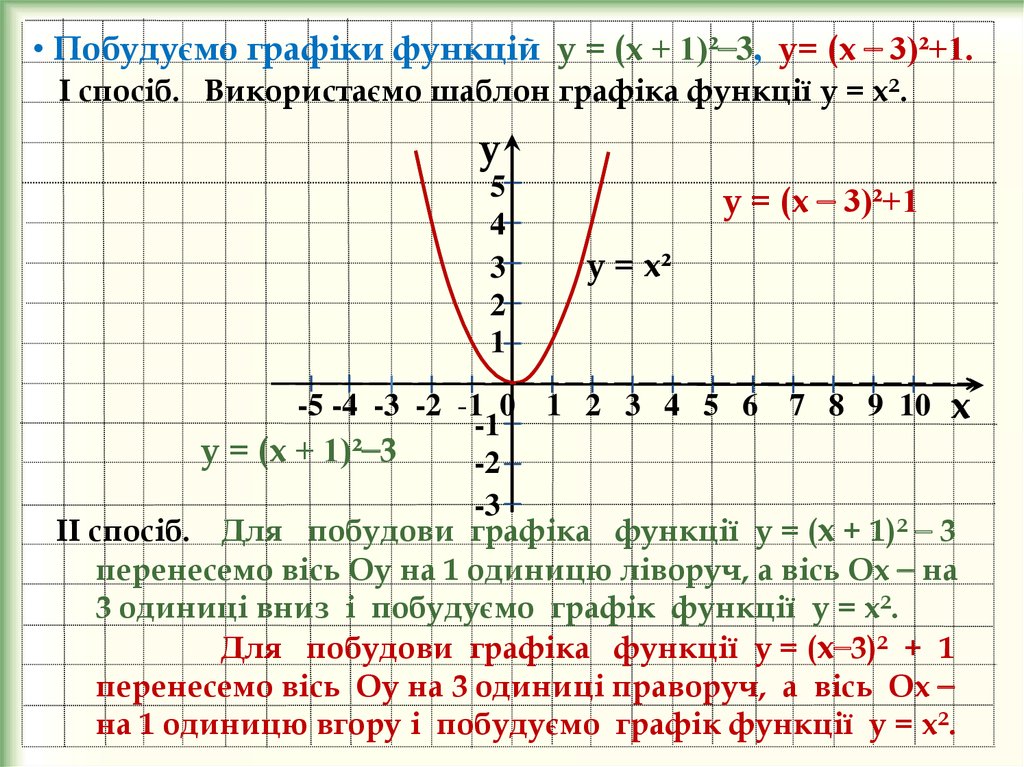
• Побудуємо графіки функцій у = (х + 1)²⎯3, у= (х ⎯ 3)²+1.І спосіб. Використаємо шаблон графіка функції у = х².
y
5
4
3
2
1
у = (х ⎯ 3)²+1
у = х²
-5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 x
-1
у = (х + 1)²⎯3
-2
-3
ІІ спосіб. Для побудови графіка функції у = (х + 1)² ⎯ 3
перенесемо вісь Оу на 1 одиницю ліворуч, а вісь Ох ⎯ на
3 одиниці вниз і побудуємо графік функції у = х².
Для побудови графіка функції у = (х⎯3)² + 1
перенесемо вісь Оу на 3 одиниці праворуч, а вісь Ох ⎯
на 1 одиницю вгору і побудуємо графік функції у = х².
14.
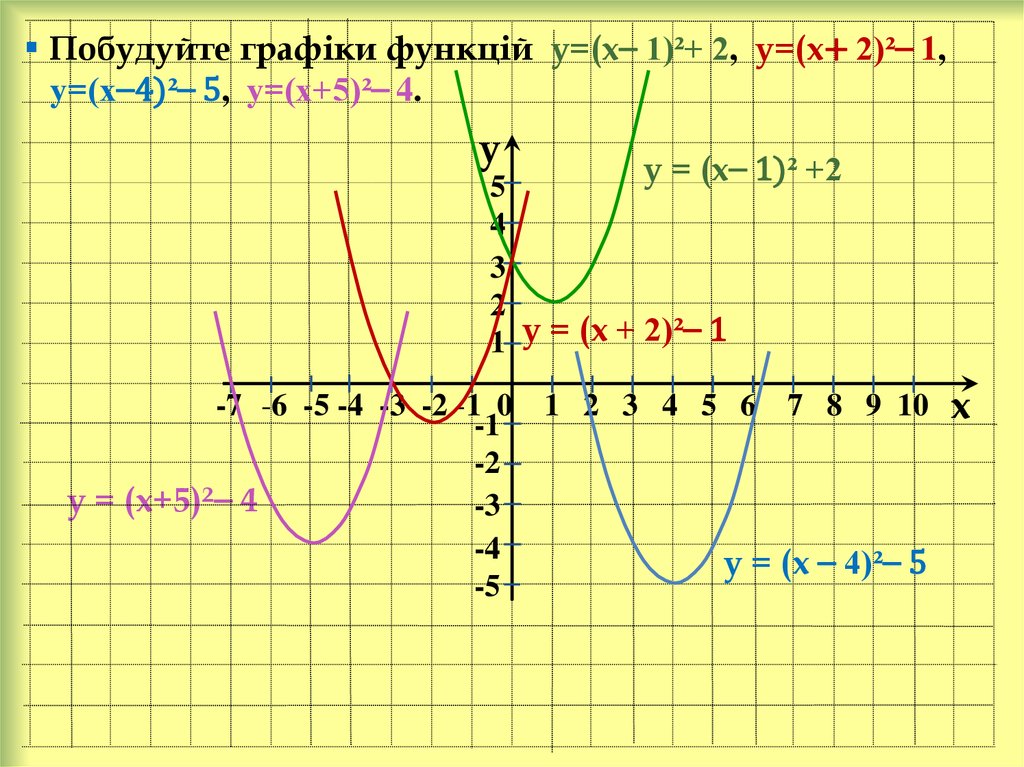
Побудуйте графіки функцій у=(х⎯ 1)²+ 2, у=(х+ 2)²⎯ 1,у=(х⎯4)²⎯ 5, у=(х+5)²⎯ 4.
y
у = (х⎯ 1)² +2
5
4
3
2
1 у = (х + 2)²⎯ 1
-7 -6 -5 -4 -3 -2 -1 0
-1
-2
у = (х+5)²⎯ 4
-3
-4
-5
1 2 3 4 5 6 7 8 9 10
у = (х ⎯ 4)²⎯ 5
x
15. 4. Побудова графіка функції y = ⎯f(x) Графік функції y= ⎯f(x) можна одержати із графіка функції y=f(x) за допомогою симетрії
відносно осі х.16.
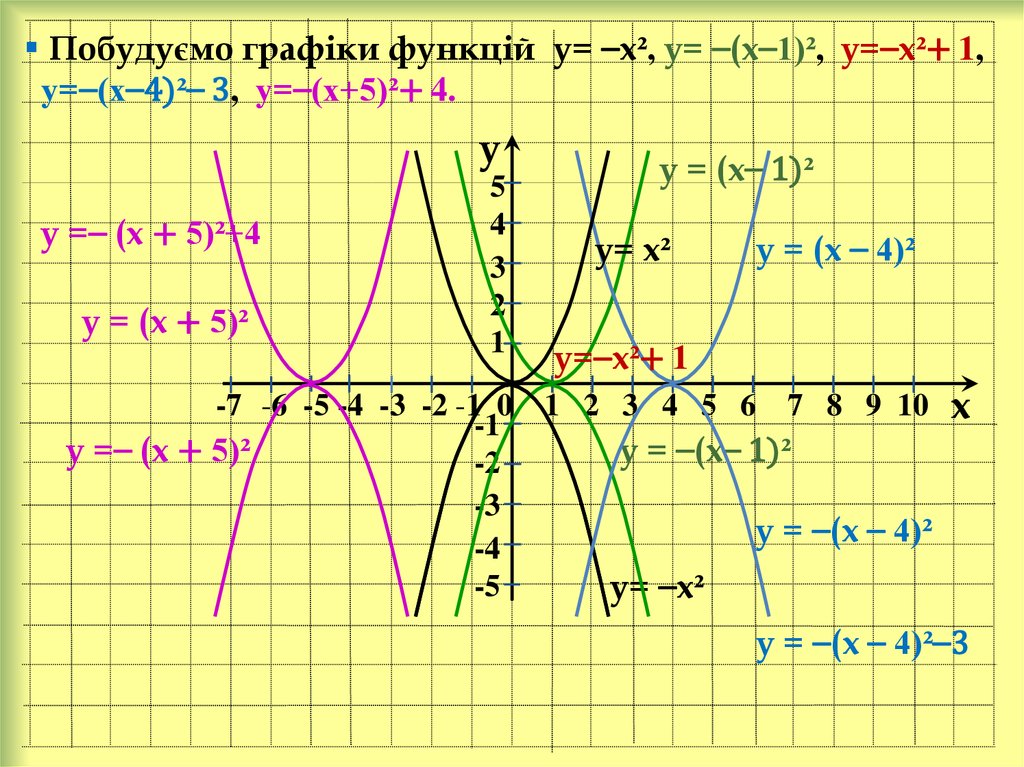
Побудуємо графіки функцій у= ⎯х², у= ⎯(х⎯1)², у=⎯х²+ 1,у=⎯(х⎯4)²⎯ 3, у=⎯(х+5)²+ 4.
y
у =⎯ (х + 5)²+4
у = (х + 5)²
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1 0
-1
у =⎯ (х + 5)²
-2
-3
-4
-5
у = (х⎯ 1)²
у= х²
у = (х ⎯ 4)²
у=⎯х²+ 1
1 2 3 4 5 6 7 8 9 10
x
у = ⎯(х⎯ 1)²
у = ⎯(х ⎯ 4)²
у= ⎯х²
у = ⎯(х ⎯ 4)²⎯3
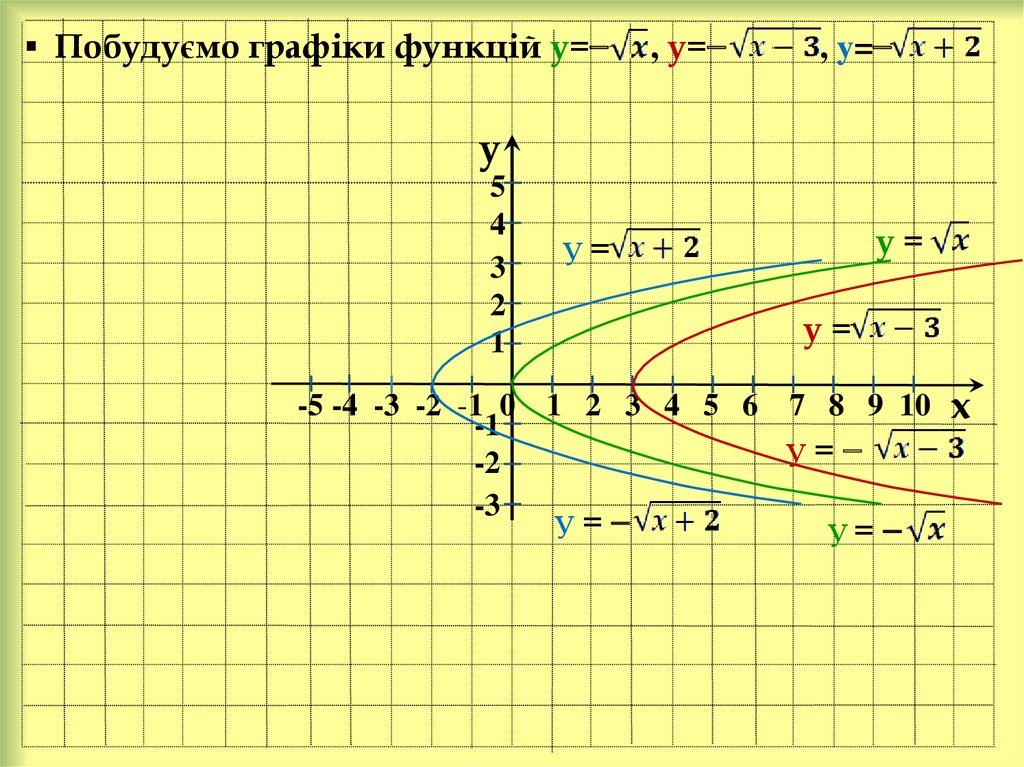
17. Побудуємо графіки функцій у=⎯ , у=⎯ , у=⎯
y5
4
3
2
1
-5 -4 -3 -2 -1 0
-1
-2
-3
У
у=
=
у=
1 2 3 4 5 6
7 8 9 10
У
У
=⎯
=⎯
У=
⎯
x
18.
Побудуйте графіки функцій у = ⎯(х+1)², у = ⎯х²+ 5,у = ⎯(х + 4)² ⎯ 3, у = ⎯(х ⎯ 5)²+ 2.
y
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1 0
-1
-2
-3
-4
-5
у = ⎯х²+ 5
у = ⎯(х ⎯ 5)² + 2
1 2 3 4 5 6 7 8 9 10
у = ⎯(х + 1)²
у = ⎯(х + 4)² ⎯ 3
x
19. 5. Побудова графіка функції y=а·f(x), де а > 0. Графік функції y=а·f(x), де а > 0, можна одержати із графіка функції y=f(x),
5. Побудова графіка функції y=а·f(x), де а > 0.Графік функції y=а·f(x), де а > 0, можна
одержати
із
графіка
функції
y=f(x),
розтягнувши від осі х в а разів, якщо а > 1,
і стиснувши його до осі х в 1/а разів, якщо
0 < а < 1.
20.
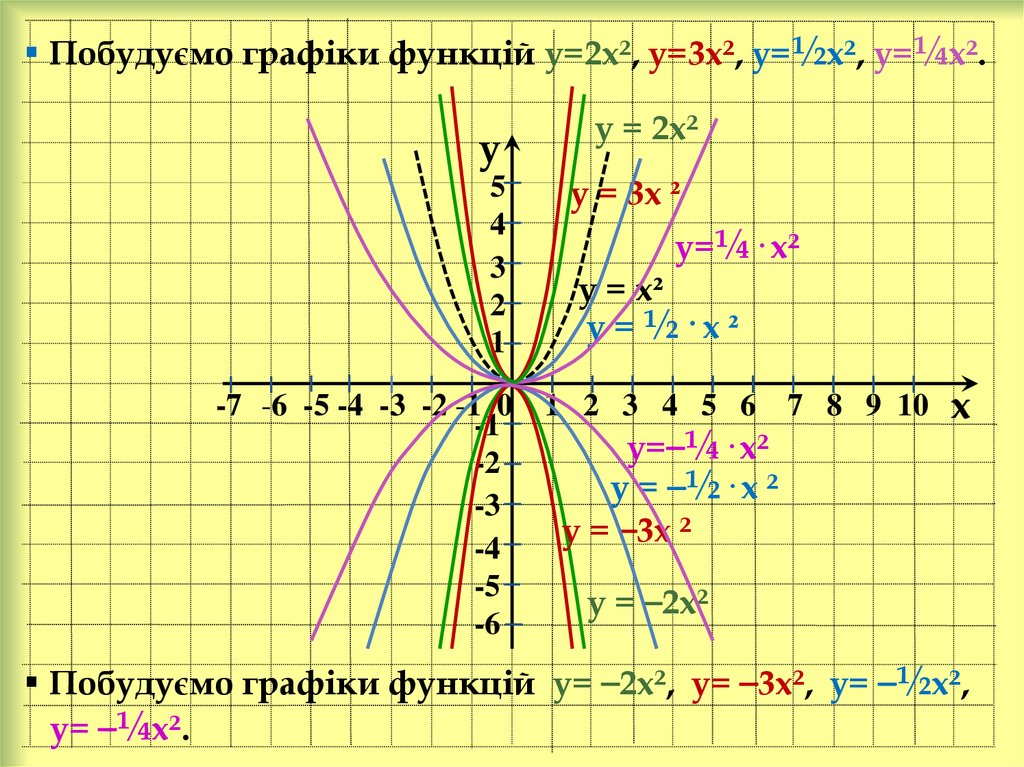
Побудуємо графіки функцій у=2х², у=3х², у=½х², у=¼х².y
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1 0
-1
-2
-3
-4
-5
-6
у = 2х²
у = 3х ²
у=¼· х²
у = х²
у = ½· х ²
1 2 3 4 5 6 7 8 9 10
у=⎯¼· х²
у = ⎯½· х ²
у = ⎯3х ²
x
у = ⎯2х²
Побудуємо графіки функцій у= ⎯2х², у= ⎯3х², у= ⎯½х²,
у= ⎯¼х².
21. 6. Побудова графіка функції y = f(⎯x). Графік функції y = f(⎯x) можна одержати із графіка функції y = f(x), відобразивши його
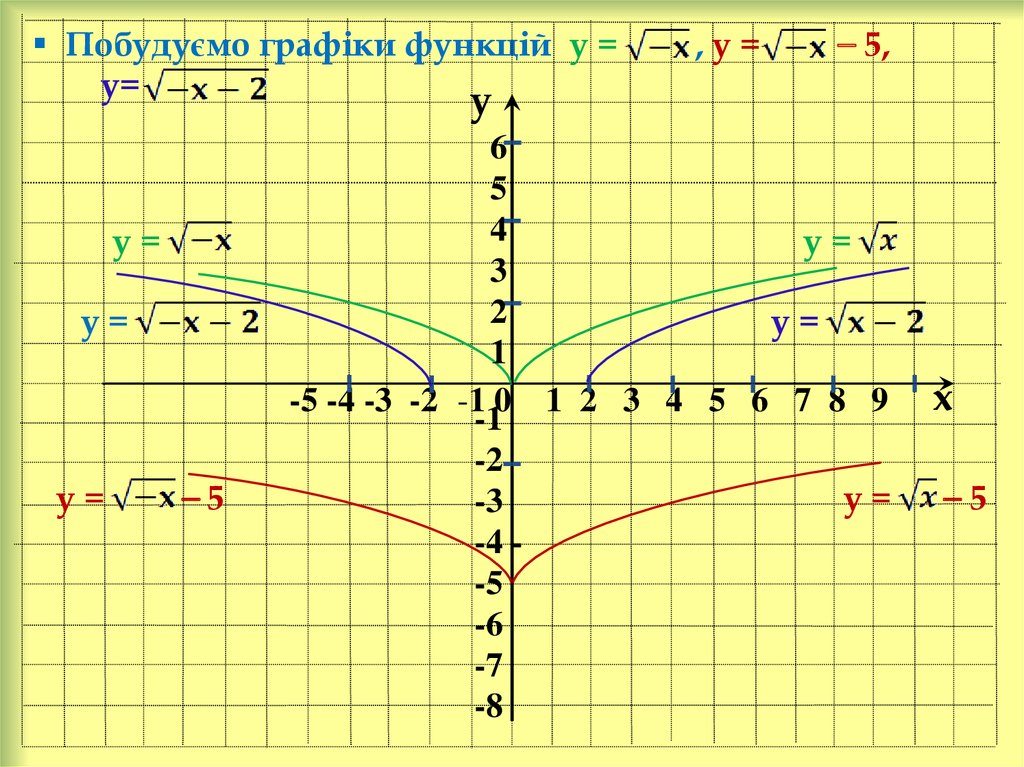
симетрично відносно осі у.22. Побудуємо графіки функцій у = , у = ⎯ 5, у=
Побудуємо графіки функцій у =у=
y
у=
у=
у=
⎯5
,у=
⎯ 5,
6
5
4
у=
3
2
у=
1
-5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9
-1
-2
у=
-3
-4 -5
-6
-7
-8
x
⎯5
23. 7. Побудова графіка функції у = |f(x)|. Графік функції y =|f(x)| можна одержати із графіка функції y = f(x), відобразивши
симетрично відносно осі х ту його частину,що розташована нижче від цієї осі х.
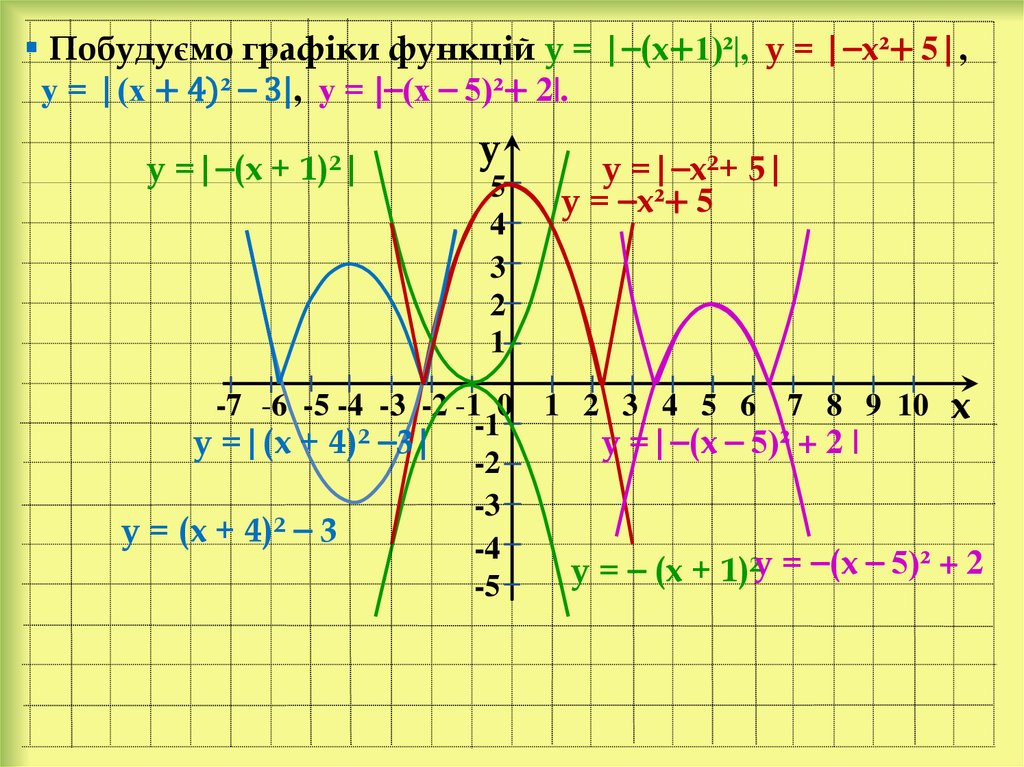
24.
Побудуємо графіки функцій у = |⎯(х+1)²|, у = |⎯х²+ 5|,у = |(х + 4)² ⎯ 3|, у = |⎯(х ⎯ 5)²+ 2|.
у =|⎯(х + 1)²|
y
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1 0
-1
у =|(х + 4)² ⎯3|
-2
-3
у = (х + 4)² ⎯ 3
-4
-5
у =|⎯х²+ 5|
у = ⎯х²+ 5
1 2 3 4 5 6 7 8 9 10
у =|⎯(х ⎯ 5)² + 2 |
x
у = ⎯ (х + 1)²у = ⎯(х ⎯ 5)² + 2
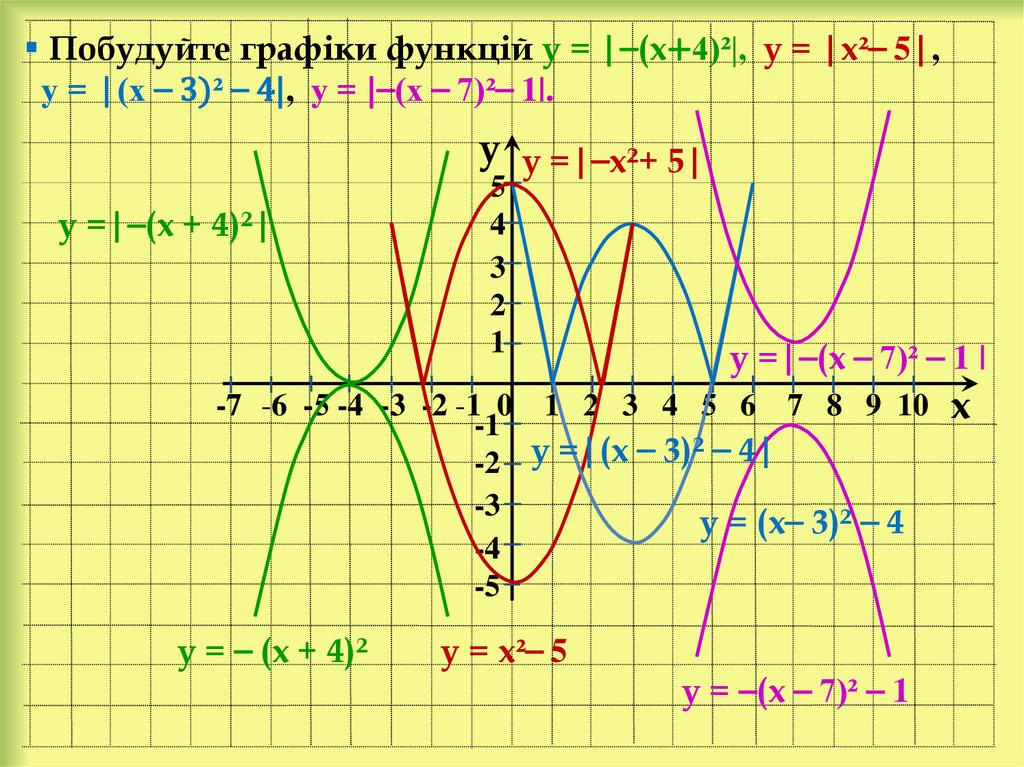
25.
Побудуйте графіки функцій у = |⎯(х+4)²|, у = |х²⎯ 5|,у = |(х ⎯ 3)² ⎯ 4|, у = |⎯(х ⎯ 7)²⎯ 1|.
y у =|⎯х²+ 5|
у =|⎯(х + 4)²|
5
4
3
2
1
у =|⎯(х ⎯ 7)² ⎯ 1 |
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
-1
-2 у =|(х ⎯ 3)² ⎯ 4|
-3
у = (х⎯ 3)² ⎯ 4
-4
-5
у = ⎯ (х + 4)²
у = х²⎯ 5
у = ⎯(х ⎯ 7)² ⎯ 1
x
26. 8. Побудова графіка функції у = f (|x|). Графік функції y = f(|x|) можна одержати із частини графіка функції y = f(x),
побудованого для х > 0 та симетричної ційчастині графіка відносно осі у.
27.
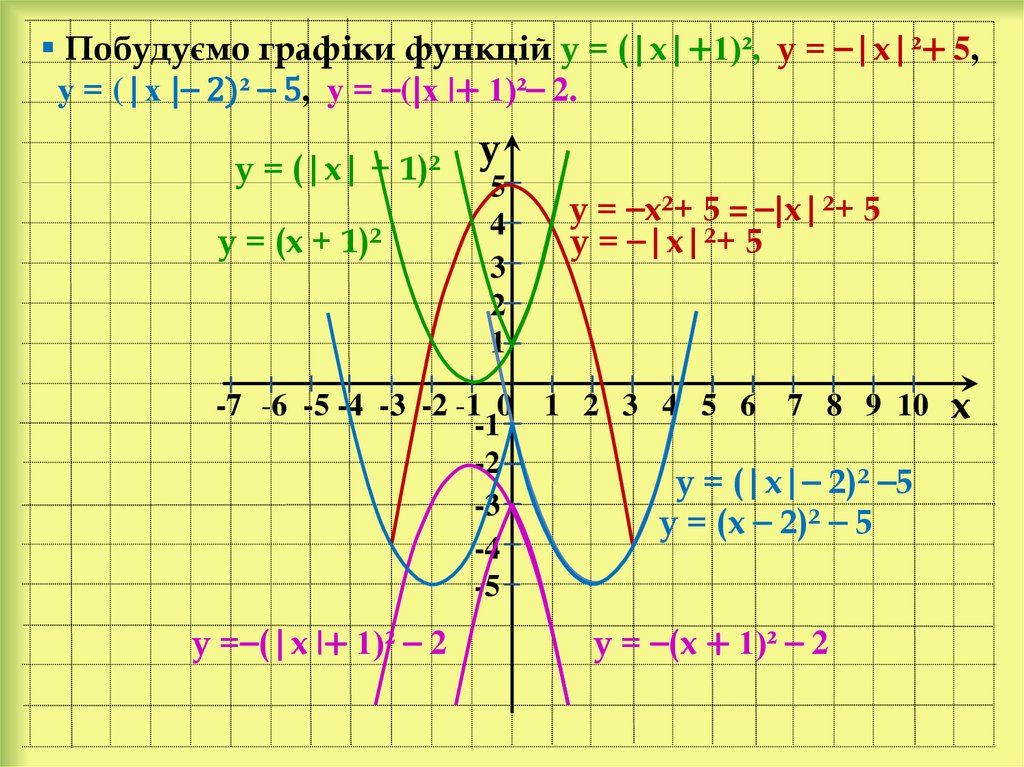
Побудуємо графіки функцій у = (|х|+1)², у = ⎯|х|²+ 5,у = (|х |⎯ 2)² ⎯ 5, у = ⎯(|х |+ 1)²⎯ 2.
у = (|х| + 1)²
у = (х + 1)²
y
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1 0
-1
-2
-3
-4
-5
у =⎯(|х |+ 1)² ⎯ 2
у = ⎯х²+ 5 = ⎯|х|²+ 5
у = ⎯|х|²+ 5
1 2 3 4 5 6 7 8 9 10
у = (|х|⎯ 2)² ⎯5
у = (х ⎯ 2)² ⎯ 5
у = ⎯(х + 1)² ⎯ 2
x
28.
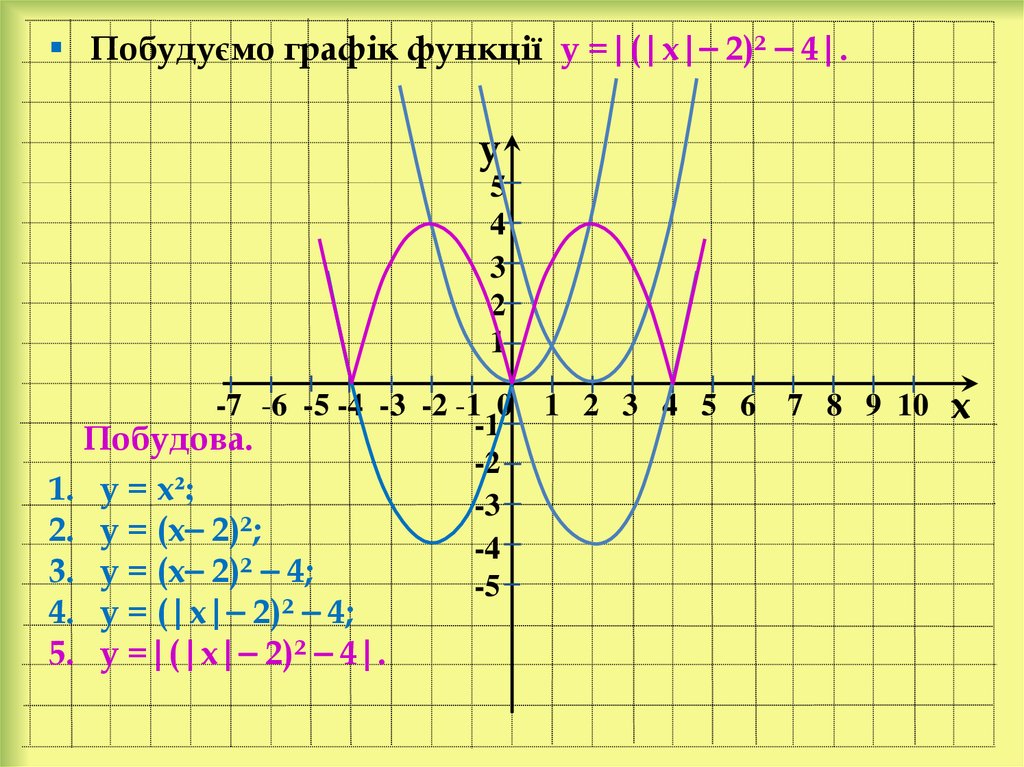
Побудуємо графік функції у =|(|х|⎯ 2)² ⎯ 4|.y
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1 0
-1
Побудова.
-2
1. у = х²;
-3
2. у = (х⎯ 2)²;
-4
3. у = (х⎯ 2)² ⎯ 4;
-5
4. у = (|х|⎯ 2)² ⎯ 4;
5. у =|(|х|⎯ 2)² ⎯ 4|.
1 2 3 4 5 6 7 8 9 10
x
29.
Побудуємо графік функції у =||х|⎯ 2 |+ 1.y
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1 0
-1
Побудова.
-2
1. у = х;
-3
2. у = |х|;
-4
3. у = |х|⎯ 2;
-5
4. у = ||х|⎯ 2|;
5. у =||х|⎯ 2 |+ 1.
1 2 3 4 5 6 7 8 9 10
x
30.
* Побудуємо графік функції у =|⎯2(|х|⎯ 1)² + 3|.y
Побудова.
1.
2.
3.
4.
5.
6.
7.
5
4
3
2
1
у = х²; -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 x
-1
у = (х⎯ 1)²;
-2
у = 2· ( х⎯ 1)²;
-3
-4
у = ⎯2· ( х⎯ 1)²;
-5
у = ⎯2· ( х⎯ 1)²+3;
у = ⎯2· ( |х|⎯ 1)²+3;
у = |⎯2· (|х|⎯ 1)²+3|.
31. Самостійна робота
32. 1. Установіть відповідність між функціями та їхніми графіками.
АБ
y
y
x
x
y
В
y
Г
x
x
А Б В Г
Функції
1 у=
2 у=
3 у=
⎯1
4 у=
1
2
⎯1
⎯1
5 у=
Х
3
+1
4
5 Х
Х
Х
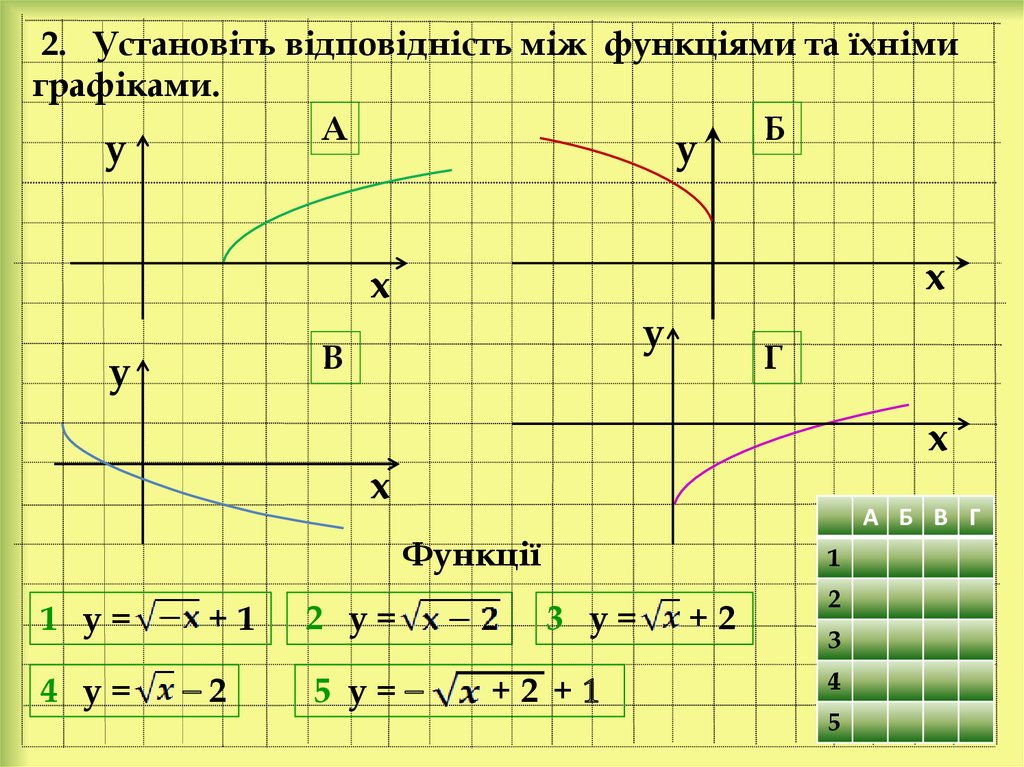
33. 2. Установіть відповідність між функціями та їхніми графіками.
АБ
y
y
x
x
y
В
y
Г
x
x
А Б В Г
Функції
1 у=
4 у=
+1
⎯2
2 у=
5 у=⎯
1
3 у=
+2 +1
+2
Х
2 Х
3
4
5
Х
Х
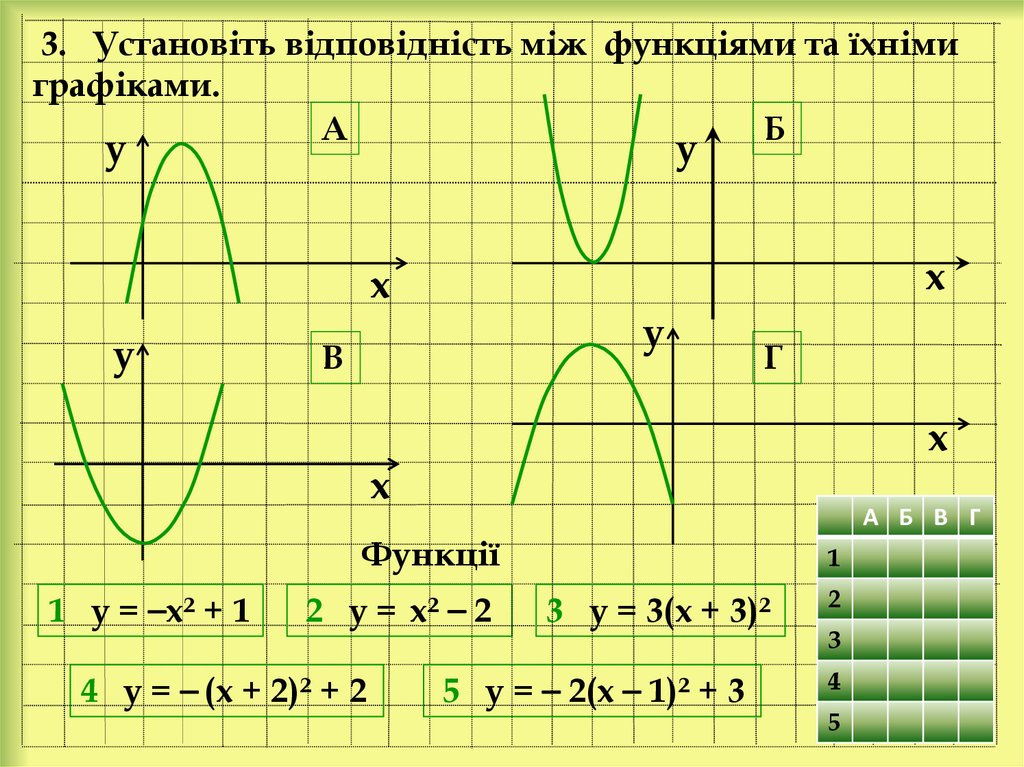
34. 3. Установіть відповідність між функціями та їхніми графіками.
АБ
y
y
x
x
y
y
В
Г
x
x
А Б В Г
Функції
1 у = ⎯х² + 1
2 у = х² ⎯ 2
4 у = ⎯ (х + 2)² + 2
1
3 у = 3(х + 3)²
5 у = ⎯ 2(х ⎯ 1)² + 3
2
3
4
5 Х
Х
Х
Х
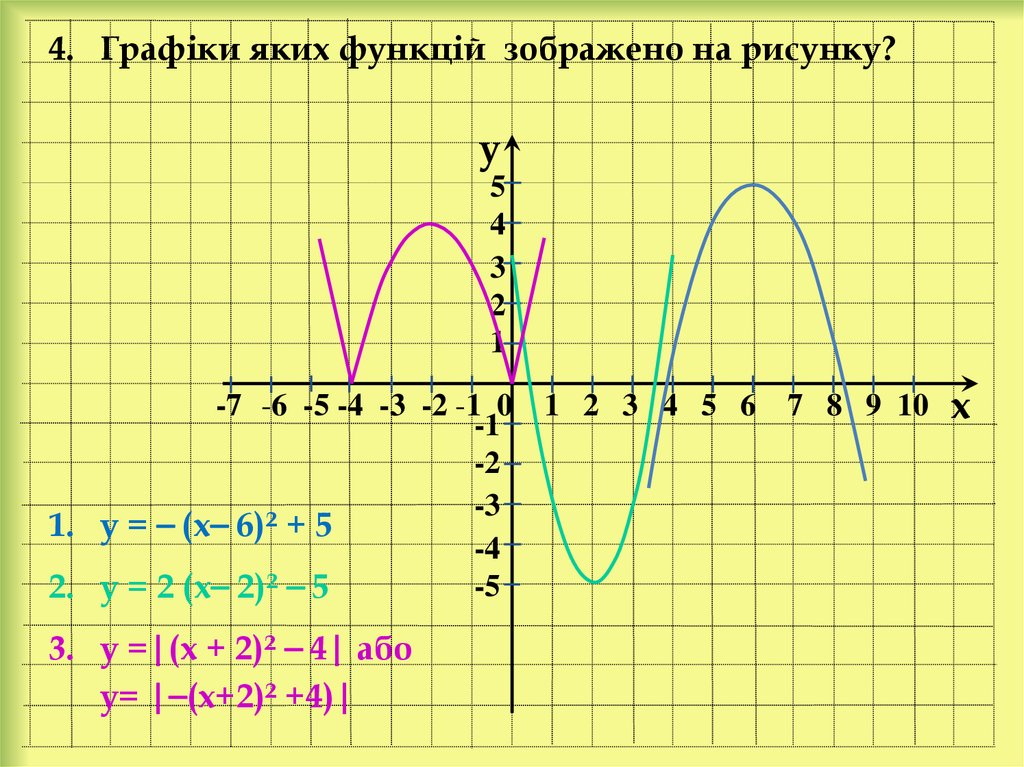
35.
4. Графіки яких функцій зображено на рисунку?y
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1 0
-1
-2
-3
1. у = ⎯ (х⎯ 6)² + 5
-4
-5
2. у = 2 (х⎯ 2)² ⎯ 5
3. у =|(х + 2)² ⎯ 4| або
у= |⎯(х+2)² +4)|
1 2 3 4 5 6 7 8 9 10
x


















 mathematics
mathematics








