Similar presentations:
Побудова графіків функцій за допомогою геометричних перетворень
1. Побудова графіків функцій за допомогою геометричних перетворень
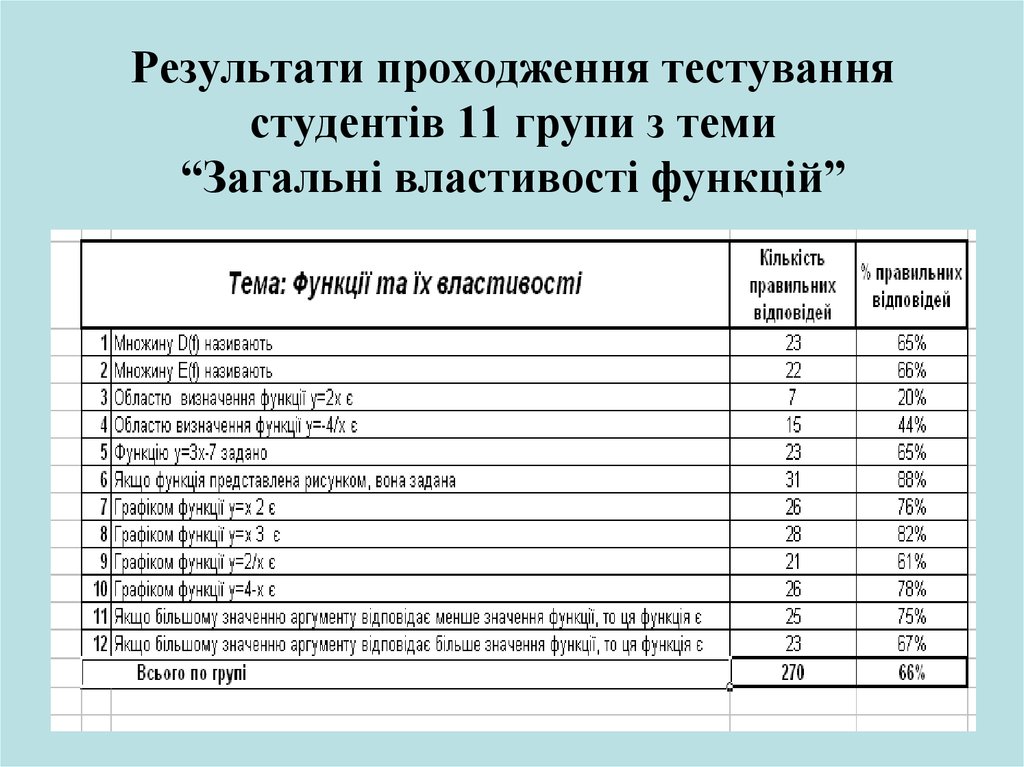
2. Результати проходження тестування студентів 11 групи з теми “Загальні властивості функцій”
3.
y 2 x 3 42
3
1
y x 1
2
y 2 1 x
4. Тема: Побудова графіків функцій за допомогою геометричних перетворень
План1.
2.
3.
4.
5.
1.
2.
Масштабування.
Симетричність.
Паралельне перенесення.
Відображення.
Побудова графіків функцій.
Література
Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки
аналізу (підручник), 10-11 кл. – К.: Зодіак – ЕКО, 2002.
Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенько А.К.
Дидактичні матеріали з математики (навчальний посібник для
студентів ВНЗ І-ІІ р.а.) – К.: Вища школа, 2001
5.
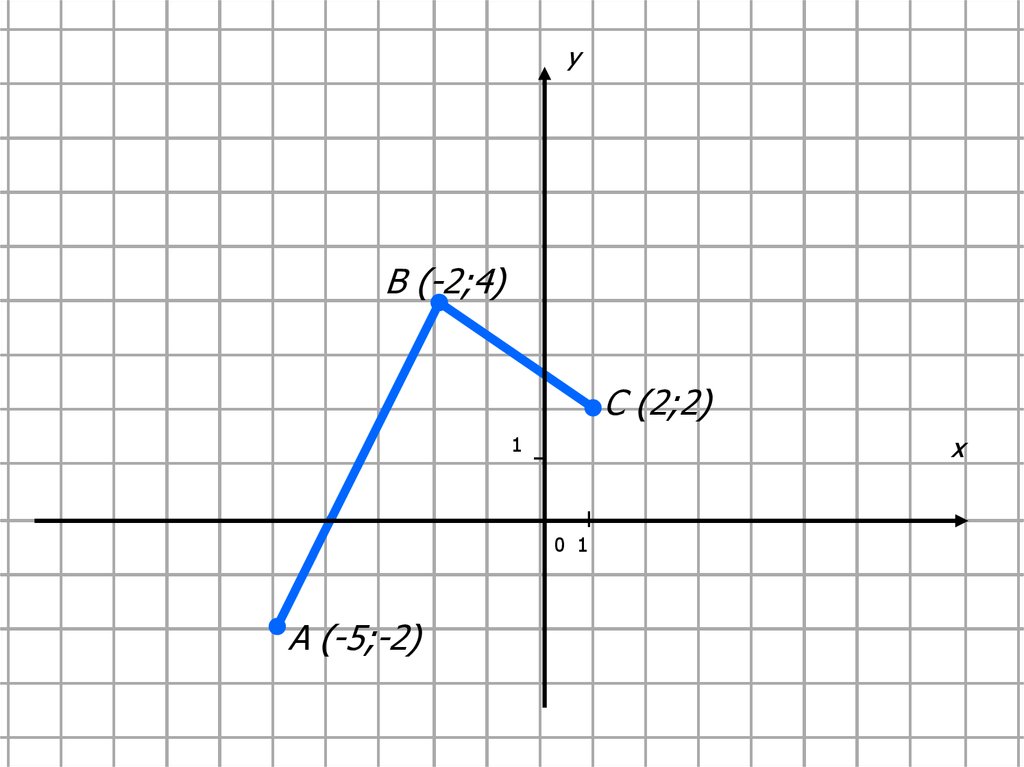
yB (-2;4)
C (2;2)
x
1
0 1
A (-5;-2)
6.
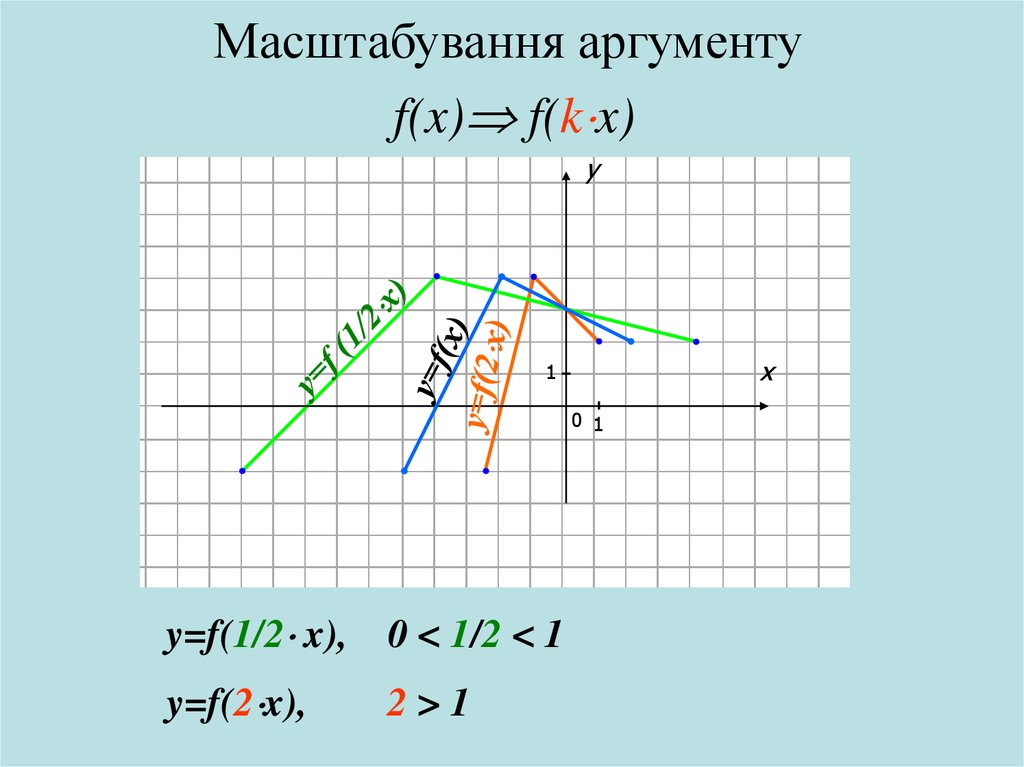
Масштабування аргументуf(x) f(k x)
y
x
1
0 1
y=f(1/2 x),
0 < 1/2 < 1
y=f(2 x),
2>1
7.
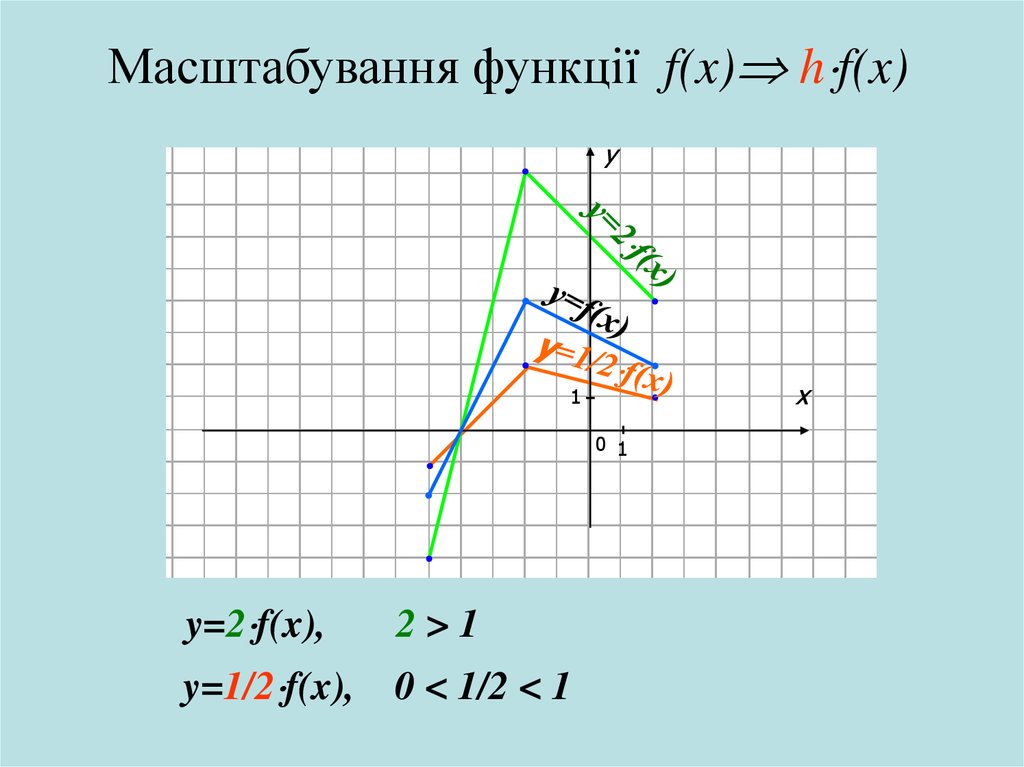
Масштабування функції f(x) h f(x)y
x
1
0 1
y=2 f(x),
2>1
y=1/2 f(x), 0 < 1/2 < 1
8.
Симетричність по аргументуf(x) f(–x)
y
1
x
0 1
9.
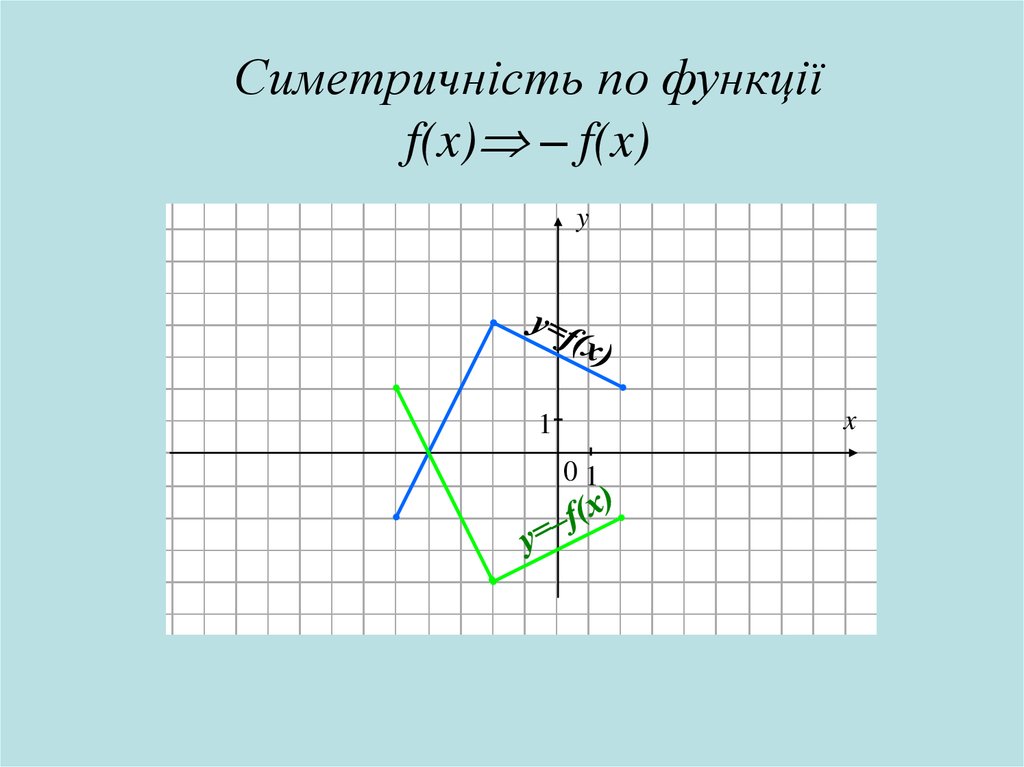
Симетричність по функціїf(x) – f(x)
y
x
1
01
10.
Паралельне перенесення по аргументуf(x) f(x–a)
y
1
x
0 1
y = f ( x – 7),
а=7>0
y = f (x+4) = f ( x –(– 4)), a = – 4 < 0
11.
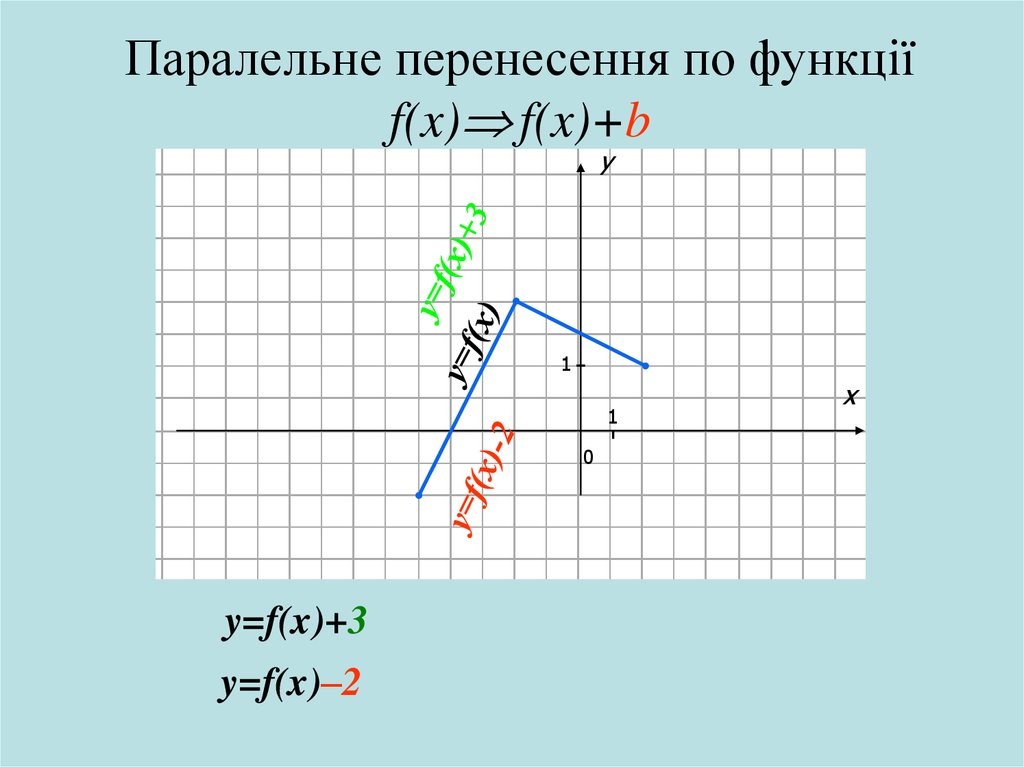
Паралельне перенесення по функціїf(x) f(x)+b
y
1
1
0
y=f(x)+3
y=f(x)–2
x
12.
Відображення відносно аргументаf(x) f(|x|)
y
x
1
0 1
13.
Відображення відносно функціїf(x) |f(x)|
y
1
x
0 1
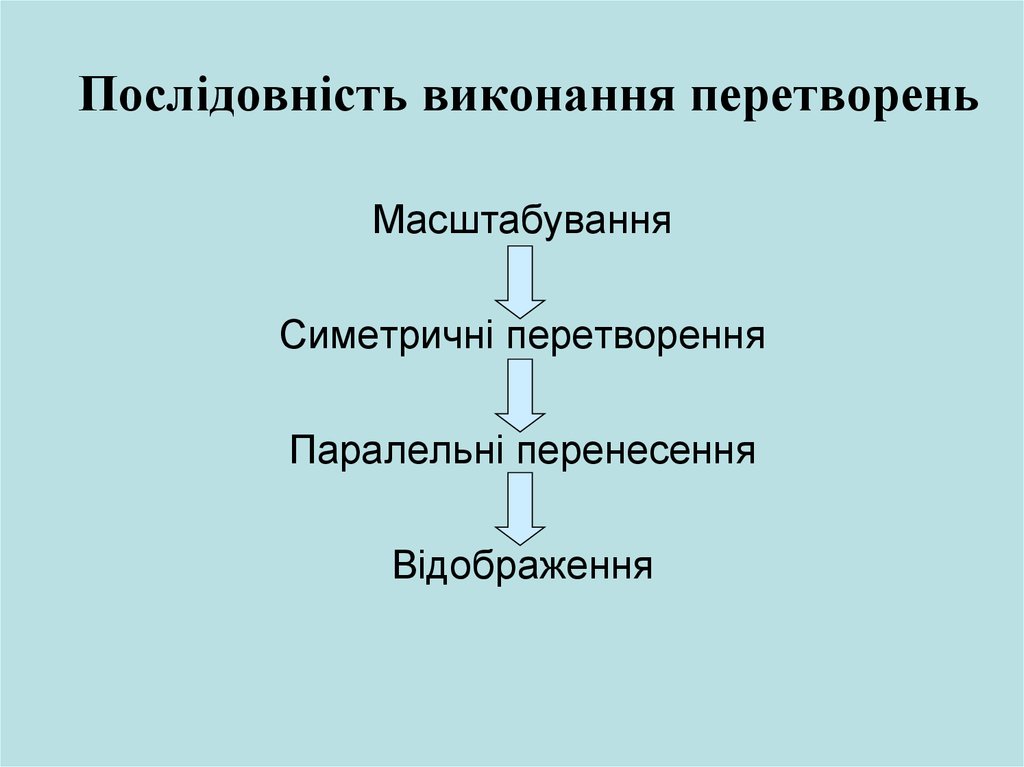
14. Послідовність виконання перетворень
МасштабуванняСиметричні перетворення
Паралельні перенесення
Відображення
15. Алгоритм побудови графіків функцій за допомогою геометричних перетворень
1. Перетворити функцію до вигляду2
y h k x a b
2. Виділити базову функцію.
3. Визначити послідовність перетворень
аргументу.
4. Визначити послідовність перетворень
функції.
5. Побудувати базовий графік.
6. Виконати перетворення графіку за
послідовністю, визначеною в п. 3.
7. Виконати перетворення графіку за
послідовністю, визначеною в п. 4.
16.
Приклад. Побудувати графік функції1. Перетворимо функцію:
y 2 x 3 4
2
y 4 x ( 3 / 2) 4
2
2. Визначимо базову функцію:
y x
2
3. Визначимо перетворення, пов’язані з аргументом:
y x ( 3 / 2) ;
2
4. Визначимо перетворення, пов’язані з функцією:
y 4 x ( 3 / 2) ;
2
y 4 x ( 3 / 2) ;
2
y 4 x ( 3 / 2) 4 ;
2
y 4 x ( 3 / 2) 4 ;
2
17.
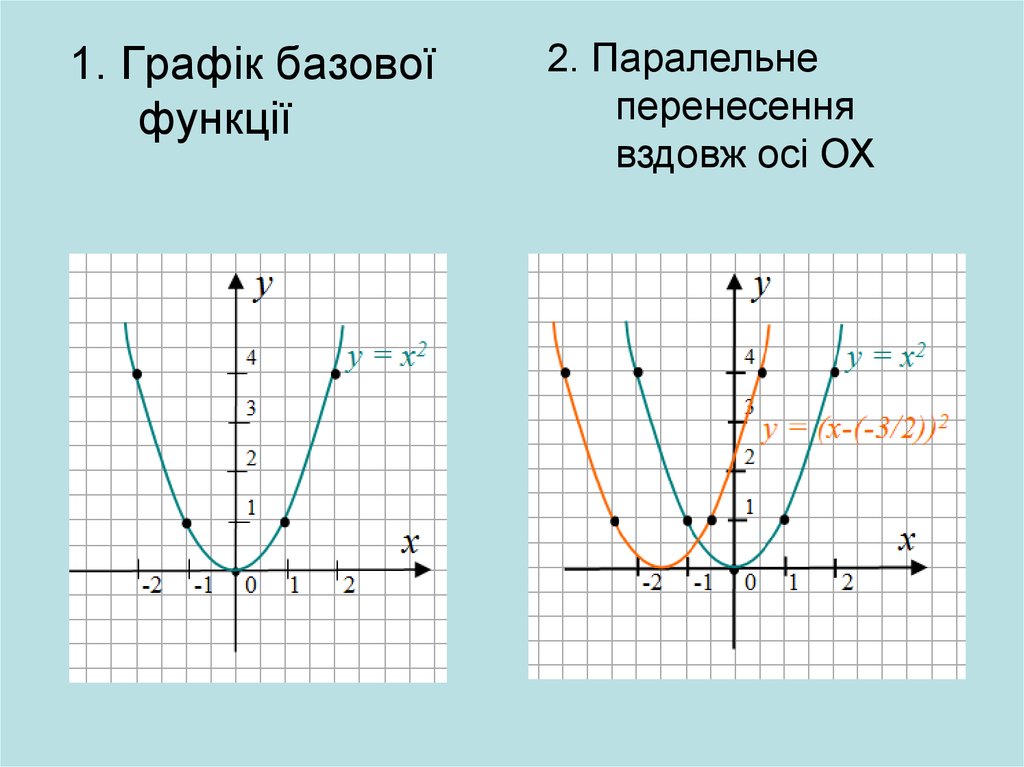
1. Графік базовоїфункції
2. Паралельне
перенесення
вздовж осі ОХ
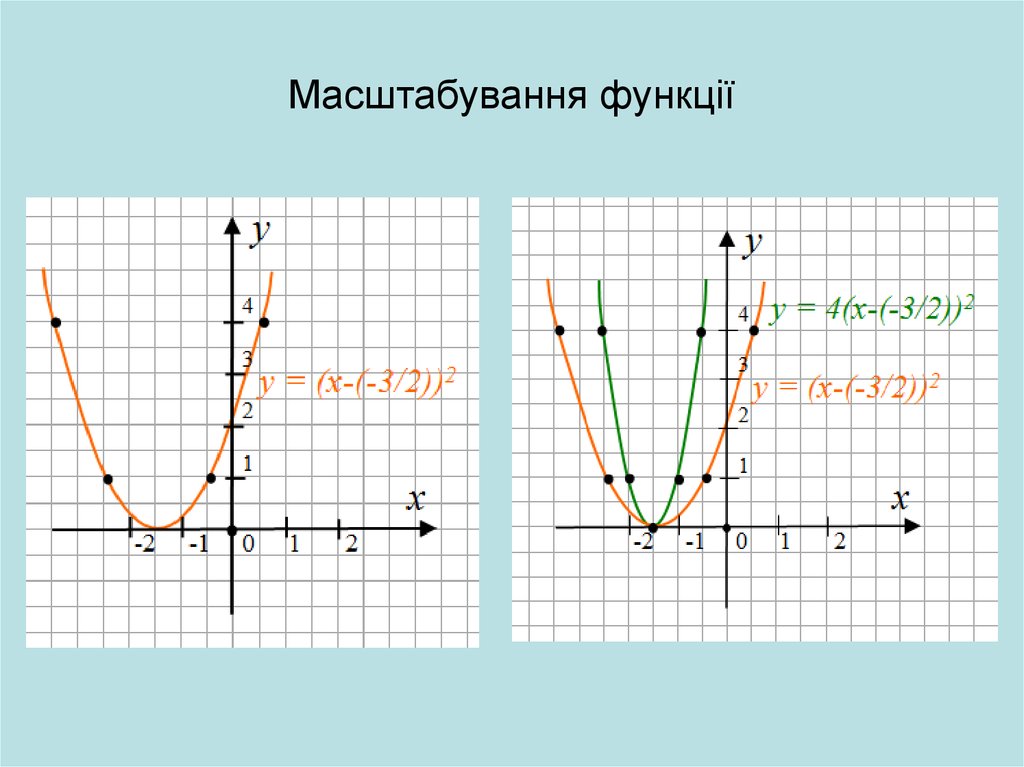
18. Масштабування функції
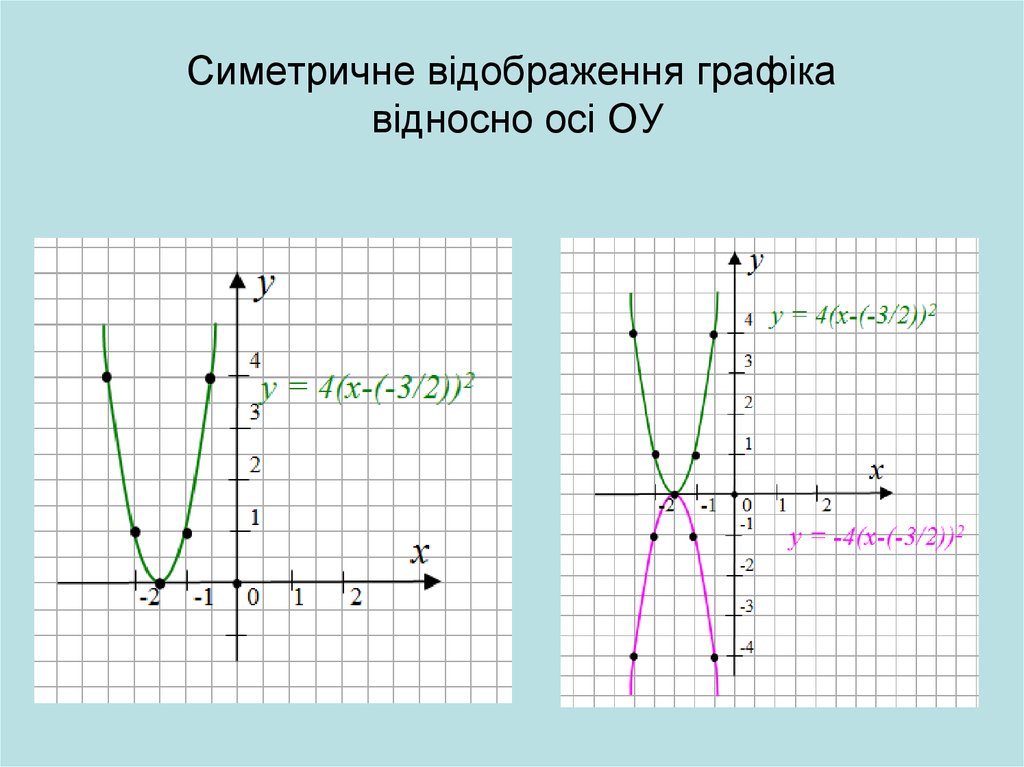
19. Симетричне відображення графіка відносно осі ОУ
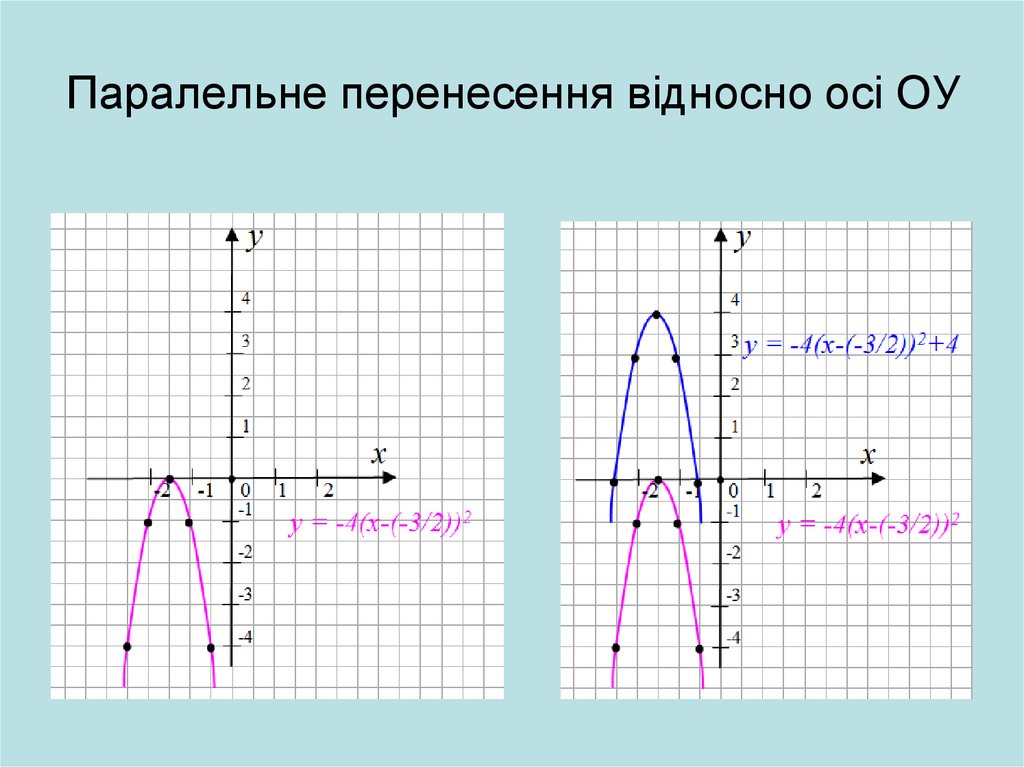
20. Паралельне перенесення відносно осі ОУ
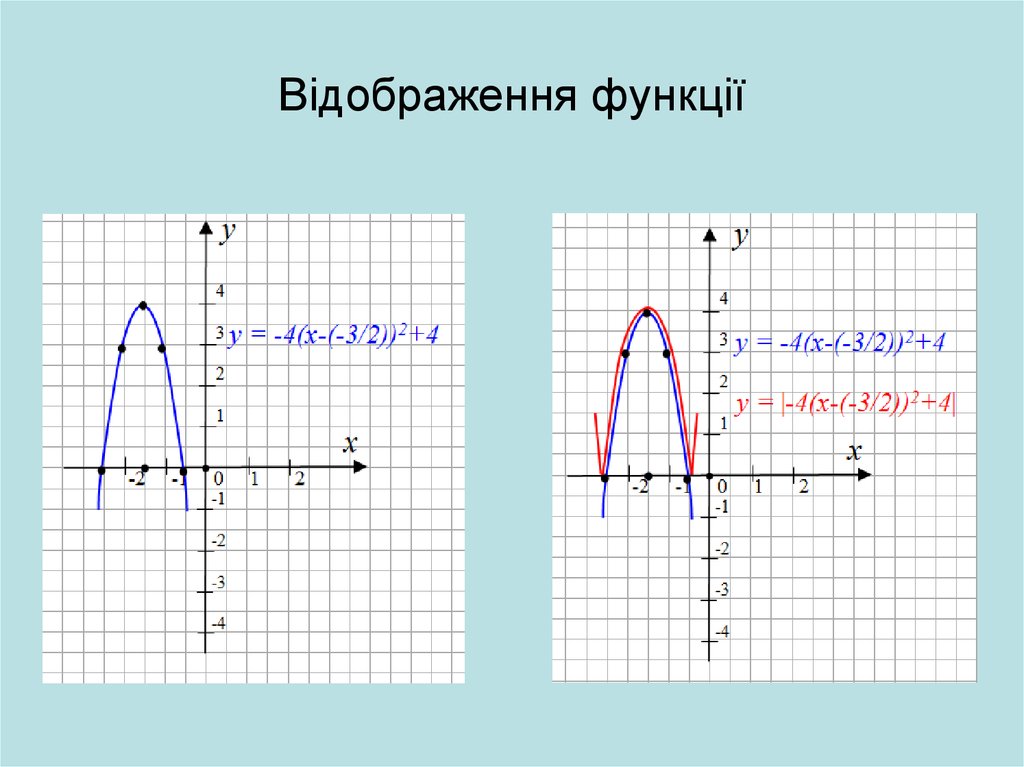
21. Відображення функції
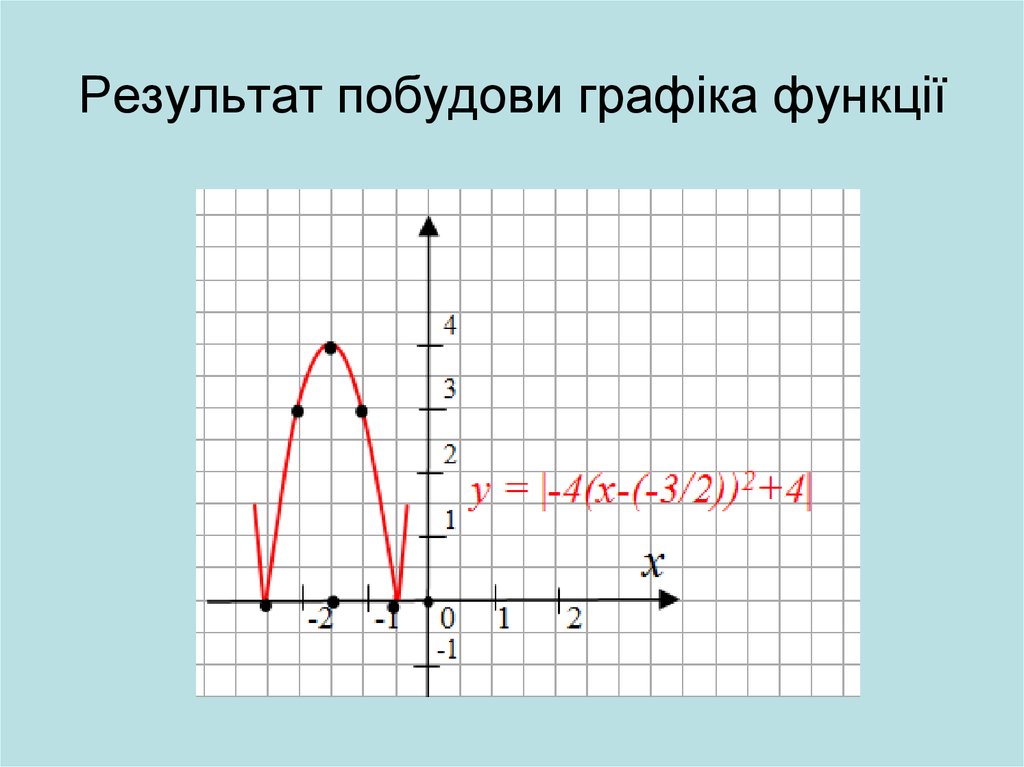
22. Результат побудови графіка функції
23.
Визначитибазові
функції
для кожного
Побудувати
графіки
функцій
рядка таблиці
y x 5
y x 5
y x 9
y x 1
6
y 2
x
7
y
3 4x
2
2
24.
Домашнє завдання:1. Вивчити перетворення графіків за
опорною таблицю.
2. За підручником:
• прочитати стор. 16-21
• виконати завдання стор. 26 № 3 (14, 30)
• додаткові завдання стор. 26 № 3 (23, 24)
25.
2Приклад 1. Побудувати графік функції, яка задана формулою y x 4 x 1.
Розв’язання.
1) Перетворимо дану формулу y x2 4 x 1 x2 2·x·2 22 4 1 x 2 3.
2
2) Побудуємо графік функції
y x 2.
3) Виконаємо паралельний перенесення
побудованого графіка на вектор 2; 3 .
y
1
0
x
1
26.
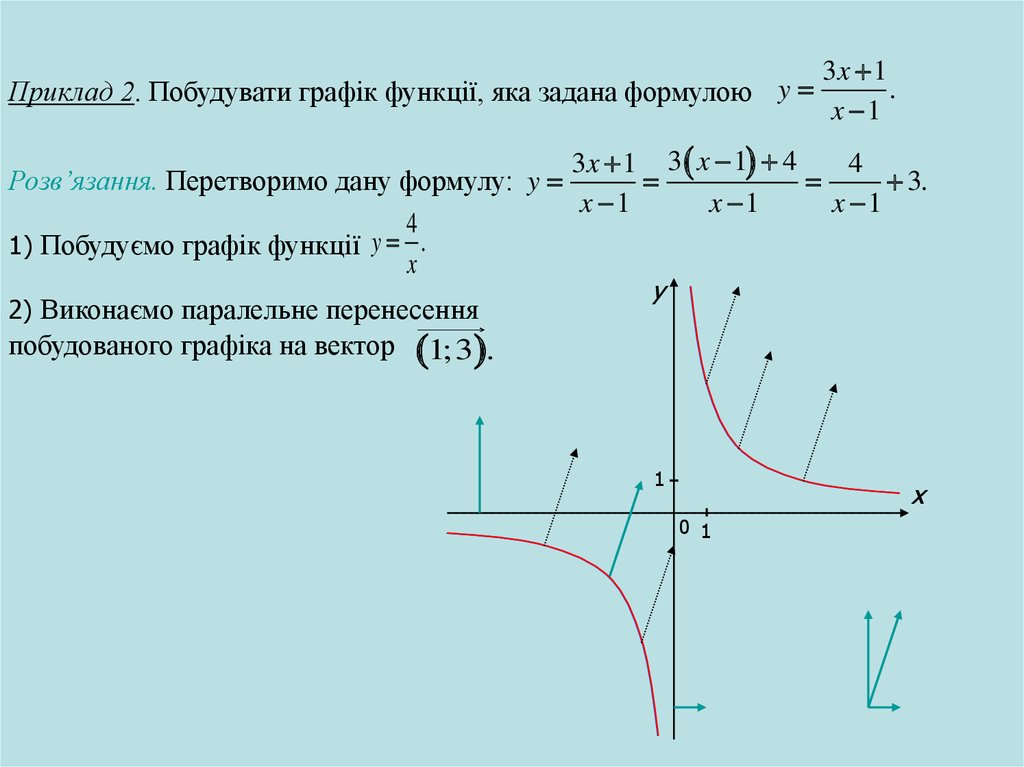
Приклад 2. Побудувати графік функції, яка задана формулою y3x 1
.
x 1
3x 1 3 x 1 4
4
Розв’язання. Перетворимо дану формулу: y
3.
x 1
x 1
x 1
4
1) Побудуємо графік функції y .
x
2) Виконаємо паралельне перенесення
побудованого графіка на вектор
y
1;3 .
1
x
0 1
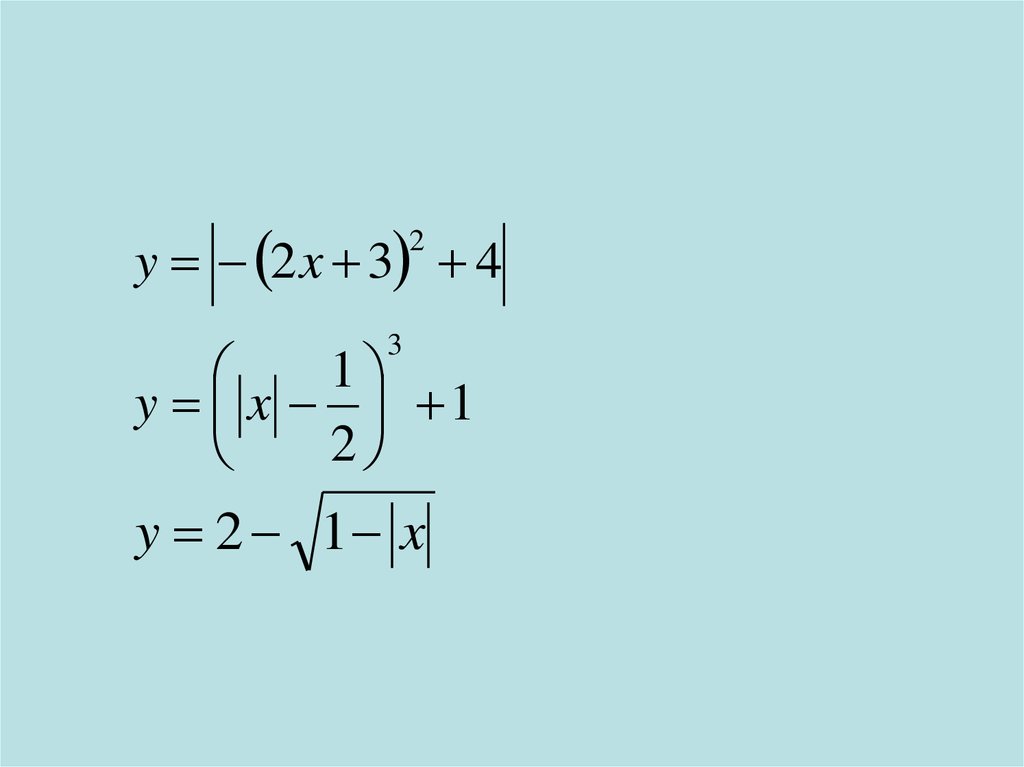










 mathematics
mathematics








