Повторення. Огляд графіків і властивостей елементарних функцій

1. Тема. Повторення. Огляд графіків і властивостей елементарних функцій. Шановні студенти конспект мати обов`язково!

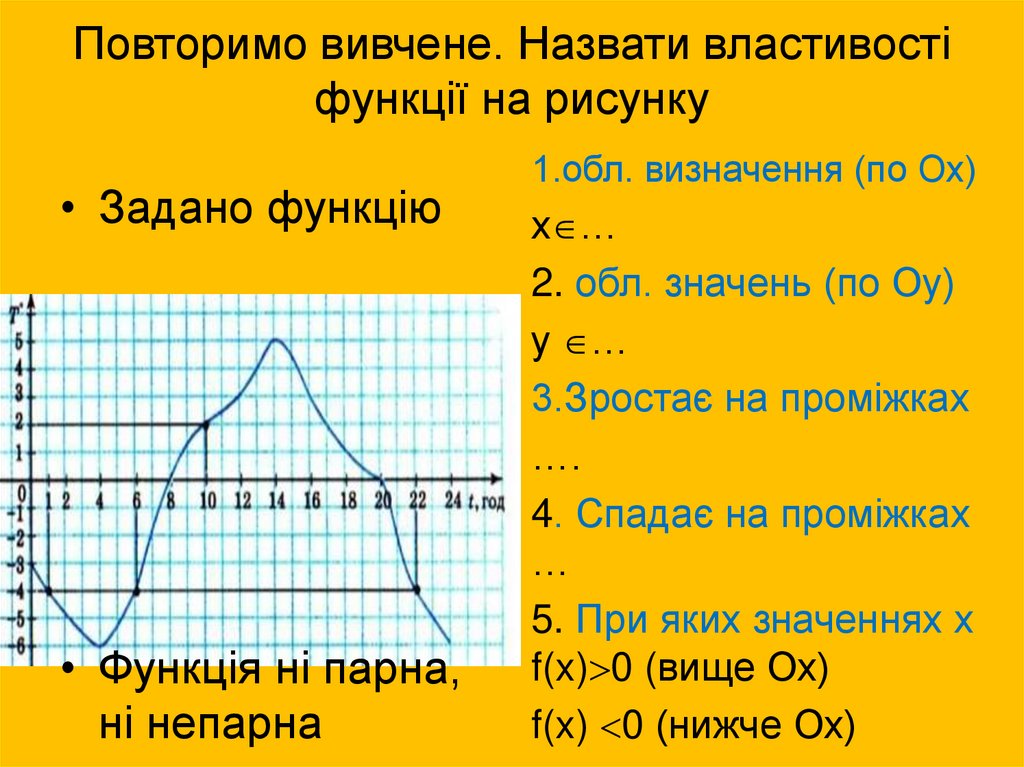
2. Повторимо вивчене. Назвати властивості функції на рисунку

• Задано функцію
• Функція ні парна,
ні непарна
1.обл. визначення (по Ох)
х …
2. обл. значень (по Оу)
у …
3.Зростає на проміжках
….
4. Спадає на проміжках
…
5. При яких значеннях х
f(x) 0 (вище Ох)
f(x) 0 (нижче Ох)

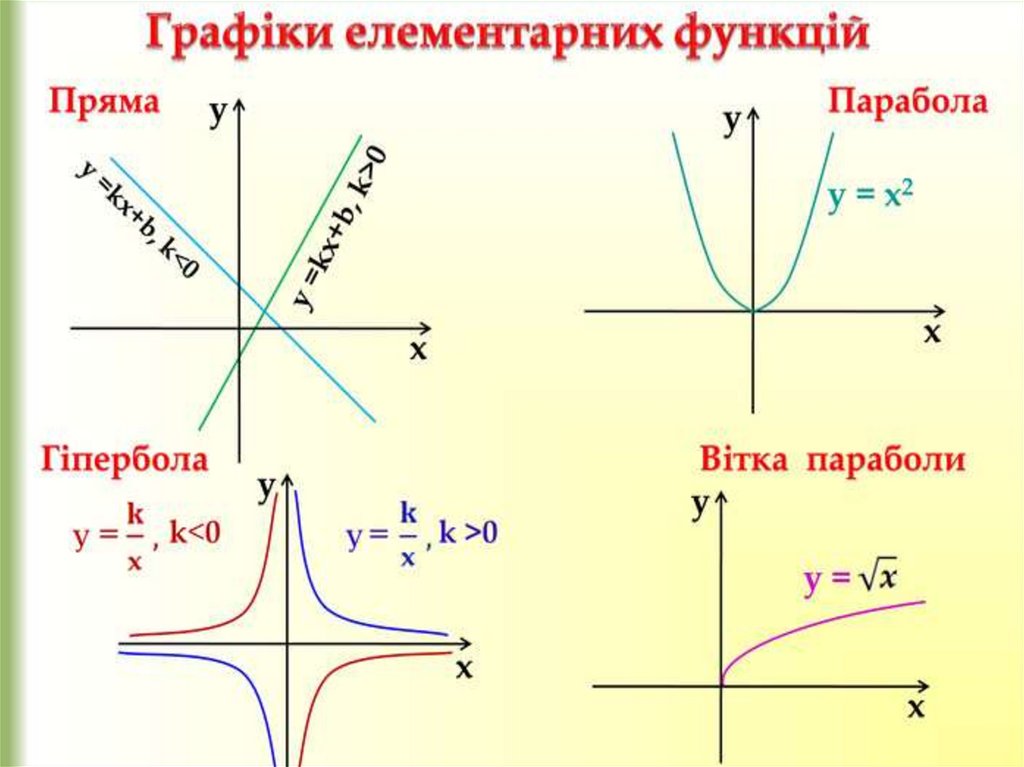
3.

4. Лінійна функція y=kx+m

• Властивості
функції y=kx+m:
• 1) D(f)=(−∞;+∞);
• 2) зростає,
якщо k>0 та спадає,
якщо k<0;
• 3) необмежена ні знизу,
ні зверху;
4) не має ні
найбільшого, ні
найменшого значень;
5) E(f)=(−∞;+∞).

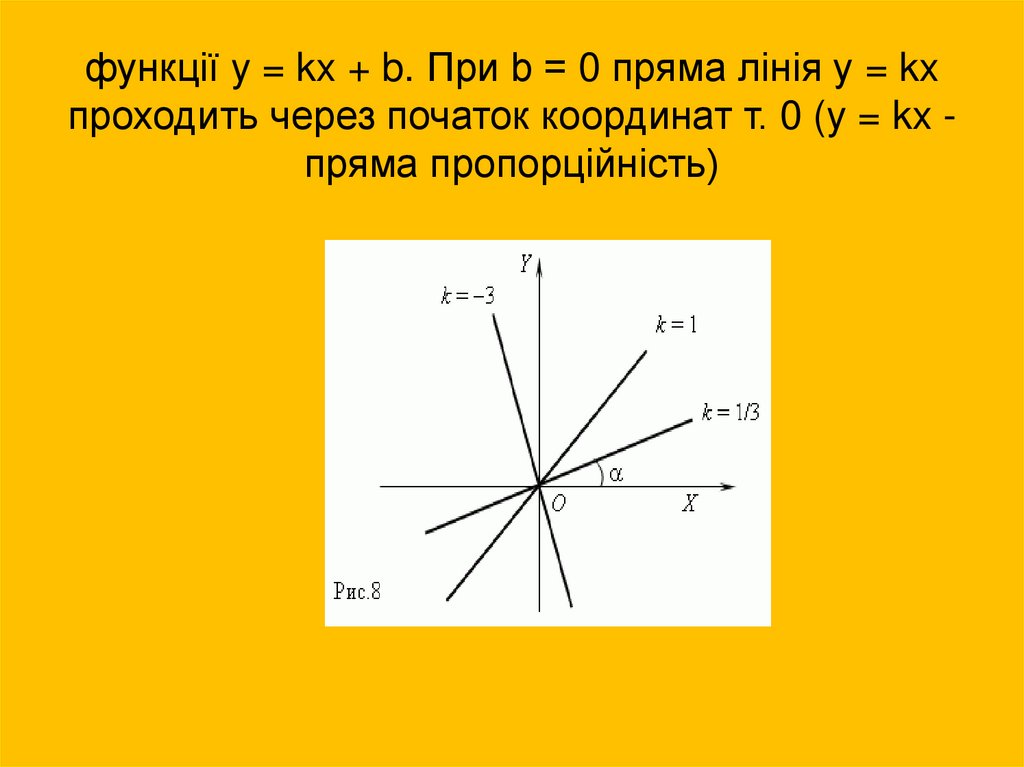
5. функції y = kx + b. При b = 0 пряма лінія y = kx проходить через початок координат т. 0 (y = kx - пряма пропорційність)

функції y = kx + b. При b = 0 пряма лінія y = kx
проходить через початок координат т. 0 (y = kx пряма пропорційність)

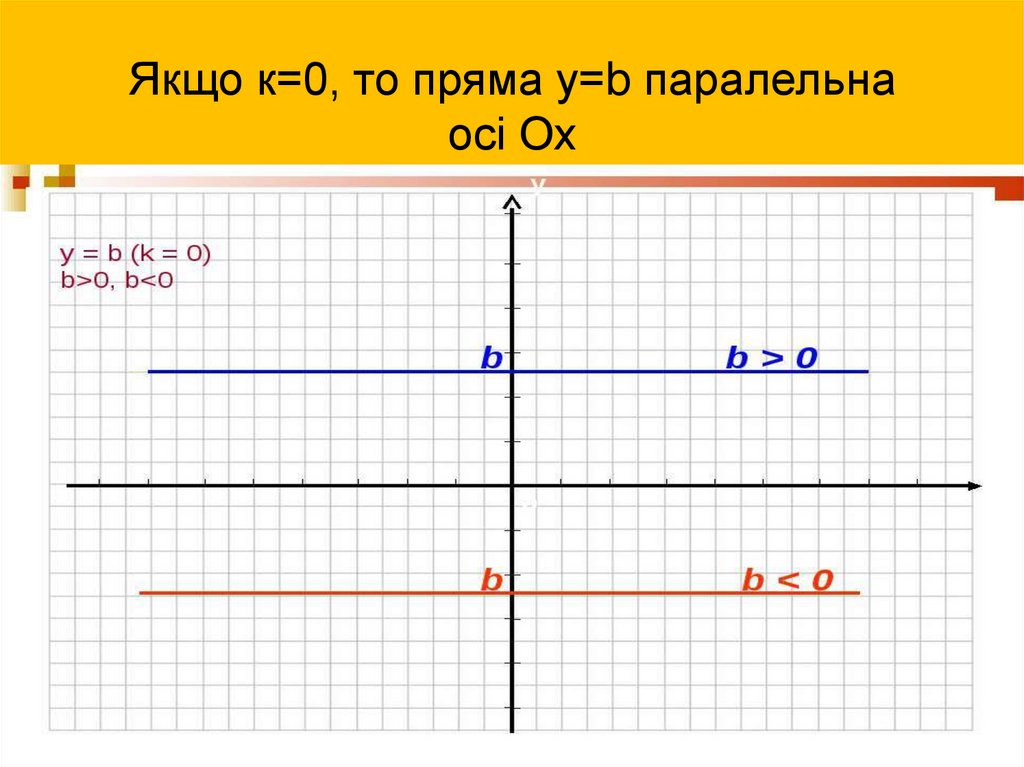
6. Якщо к=0, то пряма у=b паралельна осі Ох

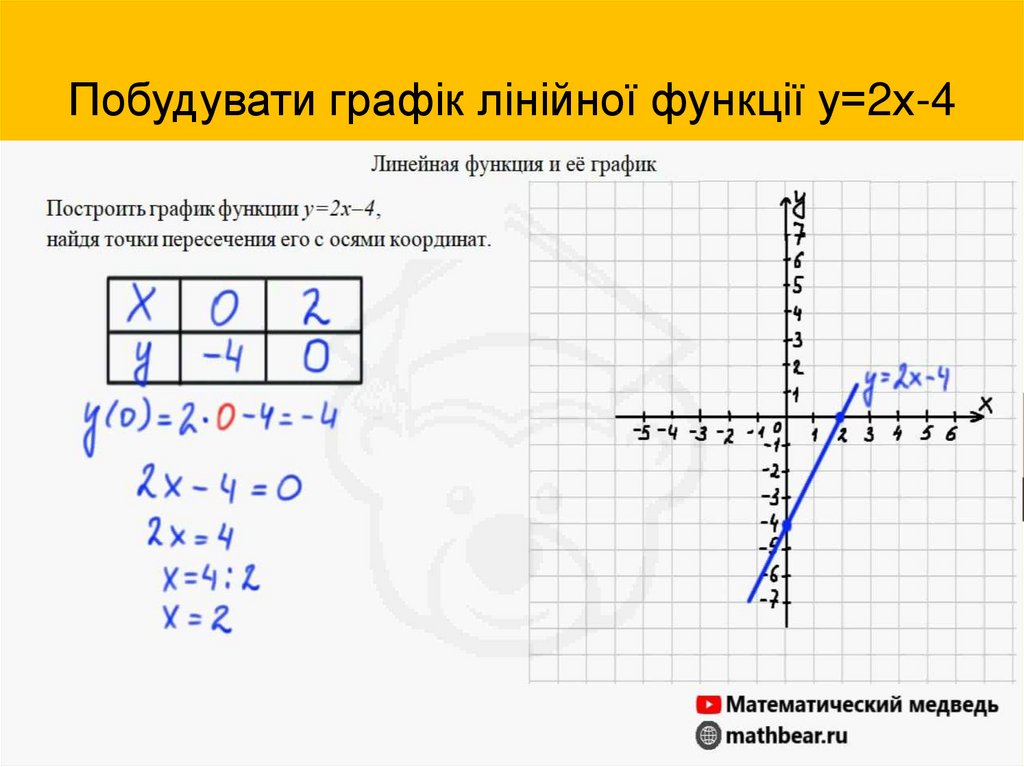
7. Побудувати графік лінійної функції у=2х-4

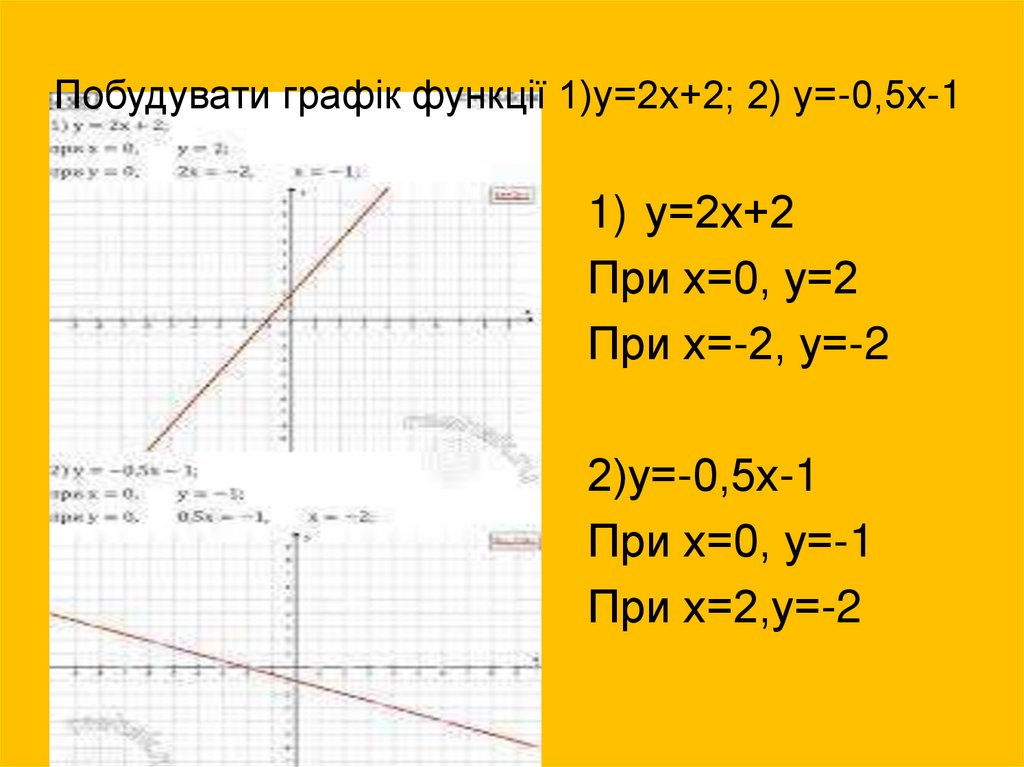
8. Побудувати графік функції 1)у=2х+2; 2) у=-0,5х-1

1) у=2х+2
При х=0, у=2
При х=-2, у=-2
2)у=-0,5х-1
При х=0, у=-1
При х=2,у=-2

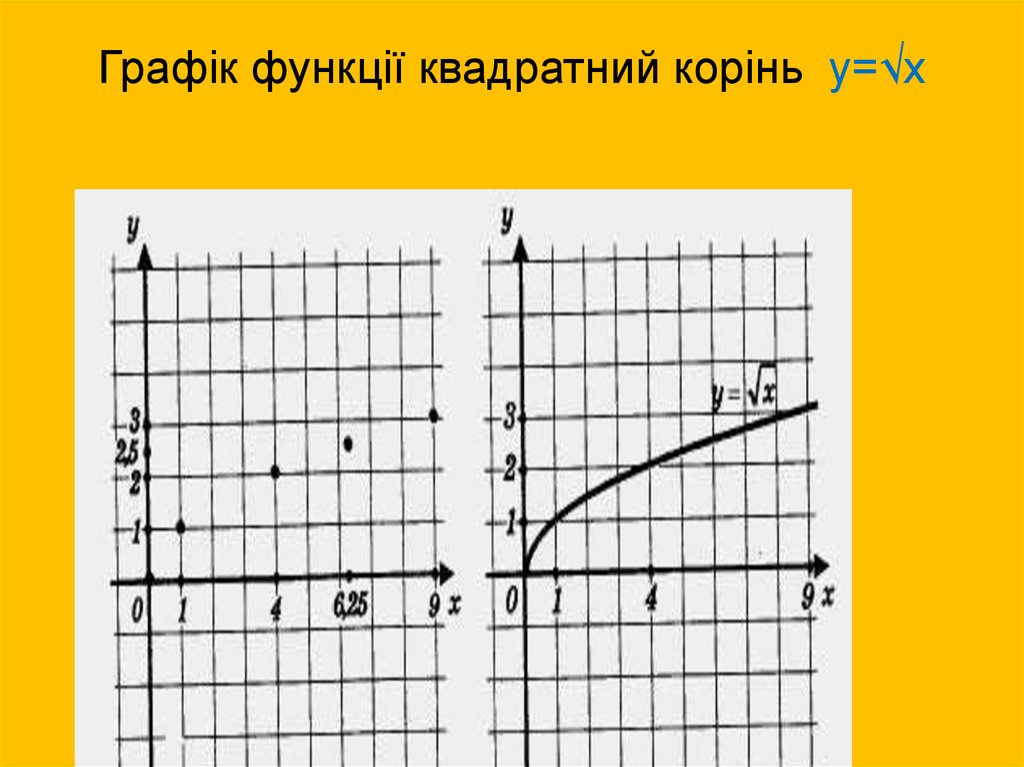
9. Графік функції квадратний корінь y=√х

10. Властивості функції y=√х

Властивості функції y=√х
Властивості функції y=√х
1 D(f)=[0;+∞);
2) зростає;
3) yнайм=0, найбільшого не існує;
4) Ні парна, ні непарна – функція
загального виду
5) E(f)=[0;+∞);

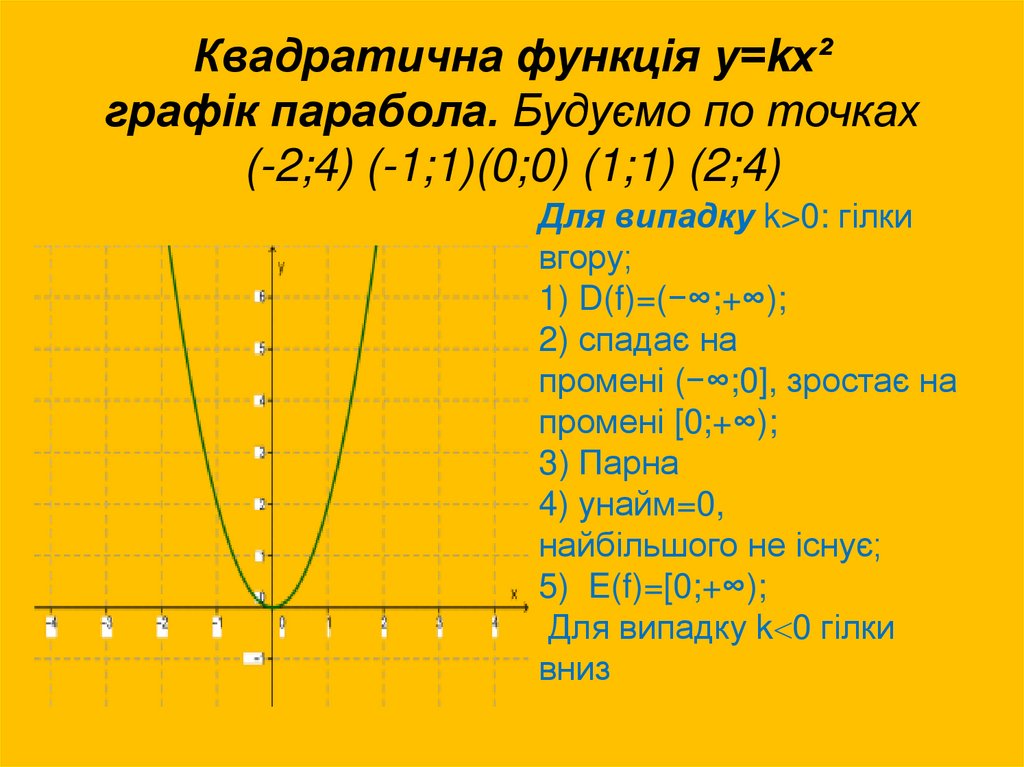
11. Квадратична функція у=kх² графік парабола. Будуємо по точках (-2;4) (-1;1)(0;0) (1;1) (2;4)

Для випадку k>0: гілки
вгору;
1) D(f)=(−∞;+∞);
2) спадає на
промені (−∞;0], зростає на
промені [0;+∞);
3) Парна
4) yнайм=0,
найбільшого не існує;
5) E(f)=[0;+∞);
Для випадку k 0 гілки
вниз

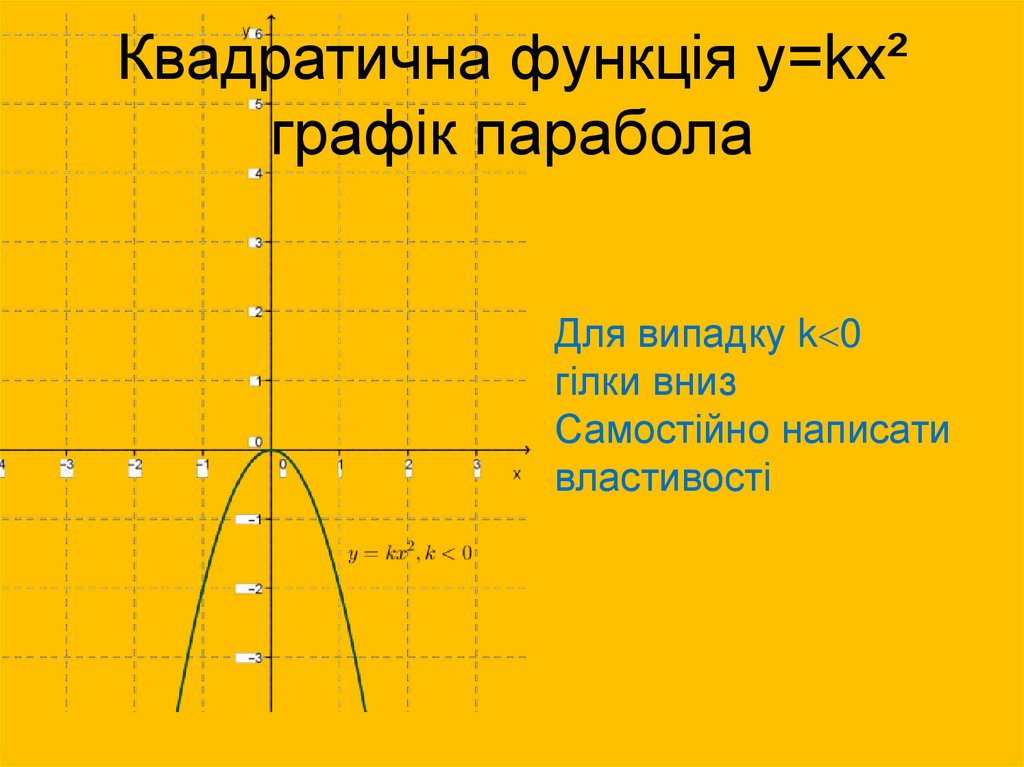
12. Квадратична функція у=kх² графік парабола

Для випадку k 0
гілки вниз
Самостійно написати
властивості

13. Кубічна функція у=kх³. Графік кубічна парабола. Будуємо по точках (-2;-8) (-1;-1)(0;0) (1;1) (2;8)

Властивості
1) D(f)=(−∞;+∞);
2) зростає, якщо k>0
спадає, якщо k<0;
3) непарна;
4) не має ні
найбільшого, ні
найменшого значень;
5) E(f)=(−∞;+∞).

14. Функція обернена пропорційність. Графік гіпербола

11
Функція уу обернена пропорційність.
хх
Графік гіпербола

15. Властивості функції 

1
Властивості функції у х
D(f)=(−∞;0) (0;+∞);
2) зростає, якщо k>0
спадає, якщо k<0;
3) непарна;
4) не має ні найбільшого,
ні найменшого значень;
5) E(f)=(−∞;+∞).

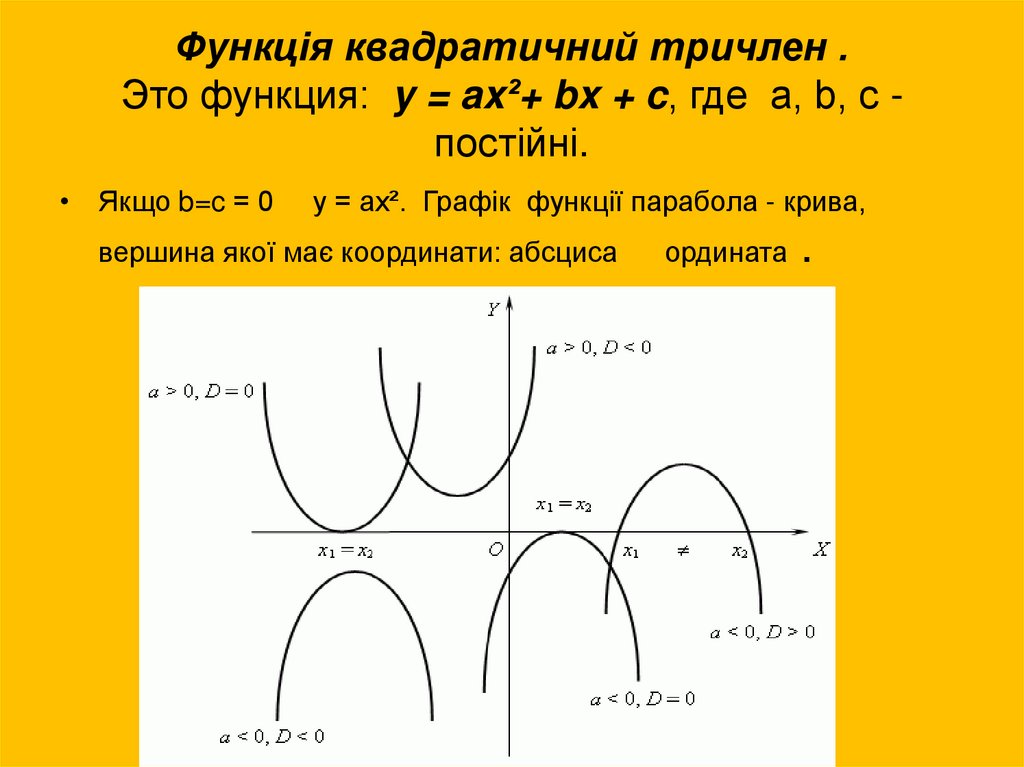
16. Функція квадратичний тричлен . Это функция: y = ax²+ bx + c, где a, b, c - постійні.

Функція квадратичний тричлен .
Это функция: y = ax²+ bx + c, где a, b, c постійні.
• Якщо b=c = 0
y = ax². Графік функції парабола - крива,
вершина якої має координати: абсциса
ордината .

17. Якщо b=c = 0 y = ax². Графік функції парабола - крива, вершина якої має координати: абсциса ордината

Якщо b=c = 0 y = ax². Графік функції парабола
- крива, вершина якої має координати:
b ордината
абсциса
у0 y ( x0 )
х
0
2a
Скільки розвязків має квадраний тричлен в кохному
випадку на рис. Попередній слайд?
Що на рис. Нулі функції?

18. Домашнє завдання. 1)Обовязково мати конспект. Вивчити властивості елементарних функцій. 2) Побудувати графіки функцій по двом

точкам1))у=5х-3; 2)у=3; 3)х=4; 4)у=-2х;
5) у=2√х скласти таблицю
6) у=2х² скласти таблицю
7)у=0,5х³ скласти таблицю
Бажаю успіху!
Прислати а пошту 7.09.22