Поняття функції. Загальні властивості функцій

1.

2.

План.
1.
2.
Поняття функції. Способи задання.
Загальні властивості функцій:
2.1. Область визначення.
2.2. Область значень.
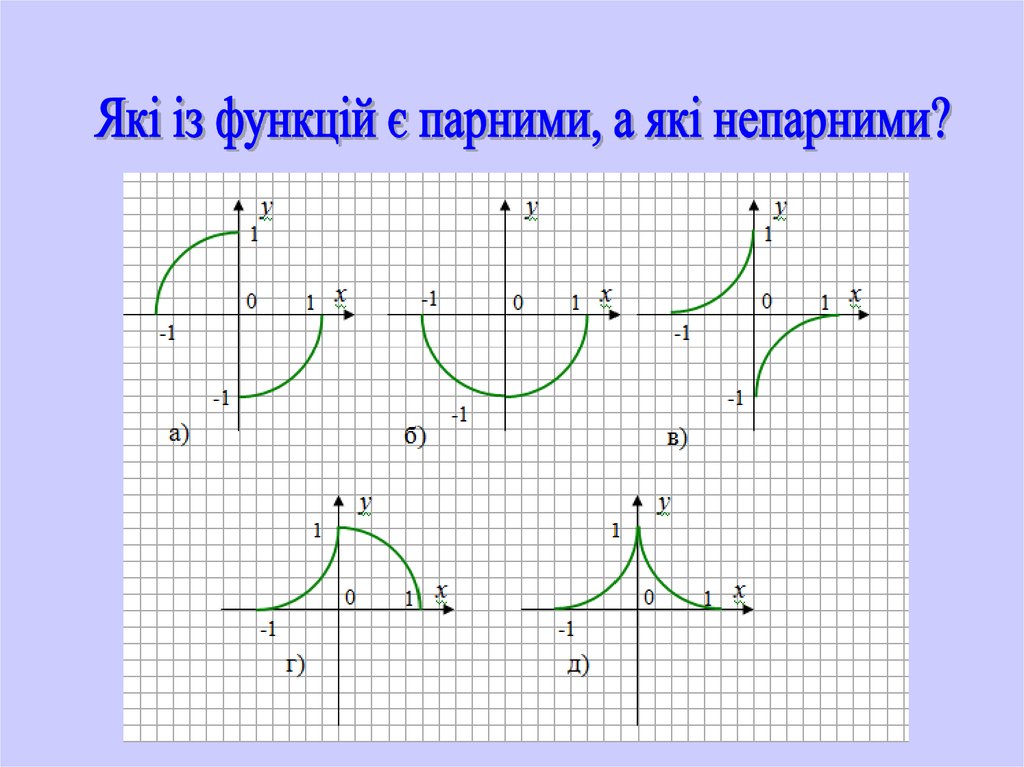
2.3. Парність.
2.4. Нулі функції.
2.5. Проміжки монотонності.
3.
Поняття оберненої функції, її графік.
1.
2.
3.
Література.
Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу
(підручник), 10-11 кл. – К.: Зодіак – ЕКО, 2002.
Бевз Г.П. Алгебра і початки аналізу (підручник для шкіл, ліцеїв,
гімназій гуманітарного напряму), 10-11 кл. – К.: ТОВ «Бліц», 2005
Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенько А.К.
Дидактичні матеріали з математики (навчальний посібник для
студентів ВНЗ І-ІІ р.а.) – К.: Вища школа, 2001

3. Функція – це залежність змінної у від змінної х, при якій кожному значенню х відповідає єдине значення у.

х – незалежна змінна або аргумент
функції
у – залежна змінна або функція

4.

Функцію позначають:
−
латинськими буквами
f, g, h... (або f(х), g(х), h(х)...)
−
рівностями у = f(х), у = g(х), у = h(х)...
Приклад 1. у = 2х + 3
−
або
f(х) = 2х + 3
Якщо задане конкретне значення незалежної змінної
х=х0, то у0 = f(х0) називається значенням функції f в
точці х0.
Приклад 2.
1. х = 5, то f(5) = 2∙ 5 + 3=10 + 3 = 13
2. f(х) = 0, тоді 2х + 3 = 0
2х = -3
х = -1,5

5.

−
−
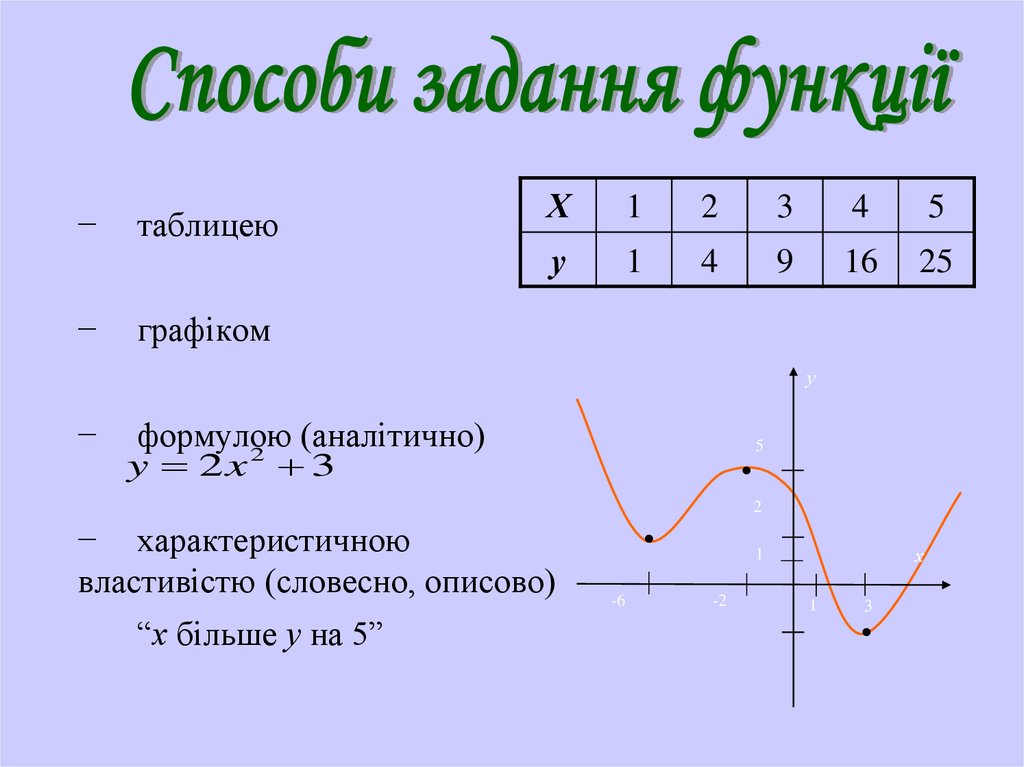
таблицею
Х
1
2
3
4
5
у
1
4
9
16
25
графіком
у
−
формулою
(аналітично)
2
5
y 2x 3
2
− характеристичною
властивістю (словесно, описово)
“х більше у на 5”
х
1
-6
-2
1
3

6.

Графіком функції у = f(х)
називається множина всіх точок
площини з координатами
(х;f(х)), де перша координата
«пробігає» всю область
визначення функції у = f(х), а
друга координата — це
відповідні значення функції в
точці х.
Y
X

7.

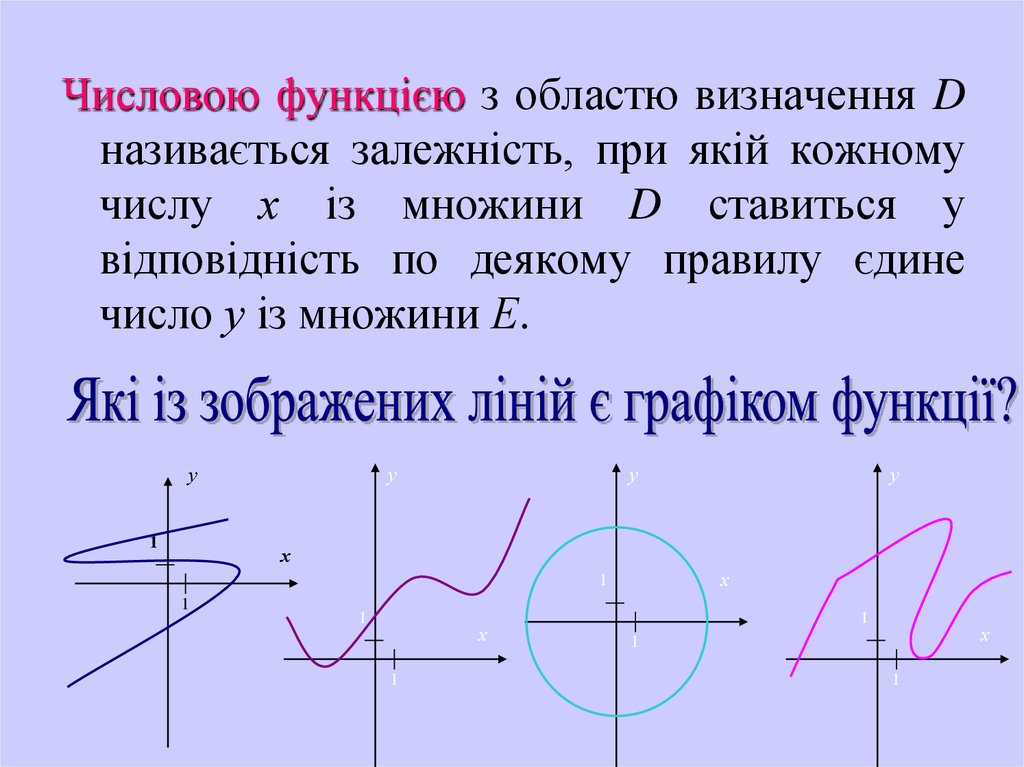
Числовою функцією з областю визначення D
називається залежність, при якій кожному
числу х із множини D ставиться у
відповідність по деякому правилу єдине
число у із множини Е.
у
1
у
у
у
х
х
1
1
1
х
1
1
х
1
1

8.

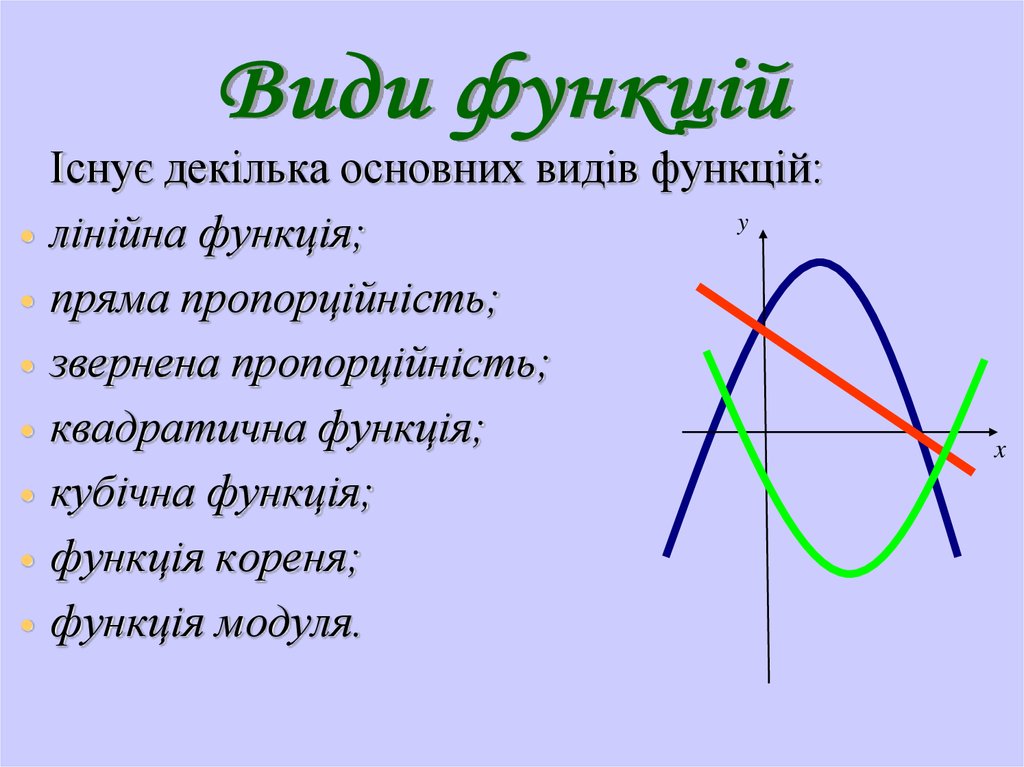
Існує декілька основних видів функцій:
y
лінійна функція;
пряма пропорційність;
звернена пропорційність;
квадратична функція;
кубічна функція;
функція кореня;
функція модуля.
x

9.

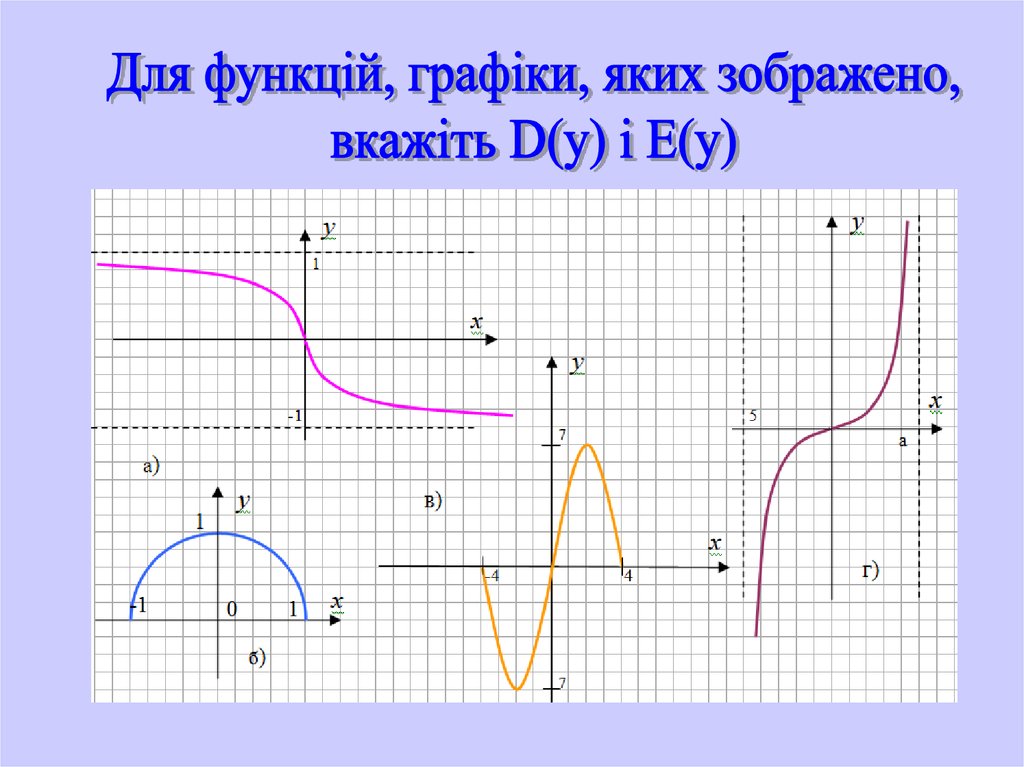
Область визначення функції у = f(х), яка
задана формулою, називається множина тих
значень, які може приймати х.
Позначення: D(
f)
Множина, яка складається із всіх чисел f(х)
таких, що х належить області визначення
функції f, називається областю значень
функції.
Позначення: Е(
f)

10.

11.

1) Якщо f(x) = P(x), де Р(х)- многочлен,
ціла раціональна функція,
то D (у) = (-∞; +∞) = R
f ( x)
2) Якщо F(x) F ( x)
- дробова функція,
g ( x)
де f(х) і g(х) — многочлени,
то слід вважати g(х) 0
(знаменник дробу не дорівнює 0).
3) Якщо функція ірраціональна y f (x) , то слід
вважати f(х) 0 (арифметичний квадратний корінь
існує тільки з невід'ємних чисел).

12.

Приклад. Знайти область визначення функції
f (х) = 2х + 3
D(f)=R або D(f) = (- ; + )
x
2) f(х) = х +
3
5x + 2
3) f(х) =
x-8
х – 8 0
х 8
D(f)=R або D(f) = (- ; + )
1)
2
D(f)= (- ; 8) (8; + )
8

13.

Для наступних функцій знайдіть D( f )
x 3x 8
y
x 6
2
y 5 2x
y 5x 2 4 x 28

14. Для наступних функцій знайдіть D( f )

Функція
у
= f(х) називається
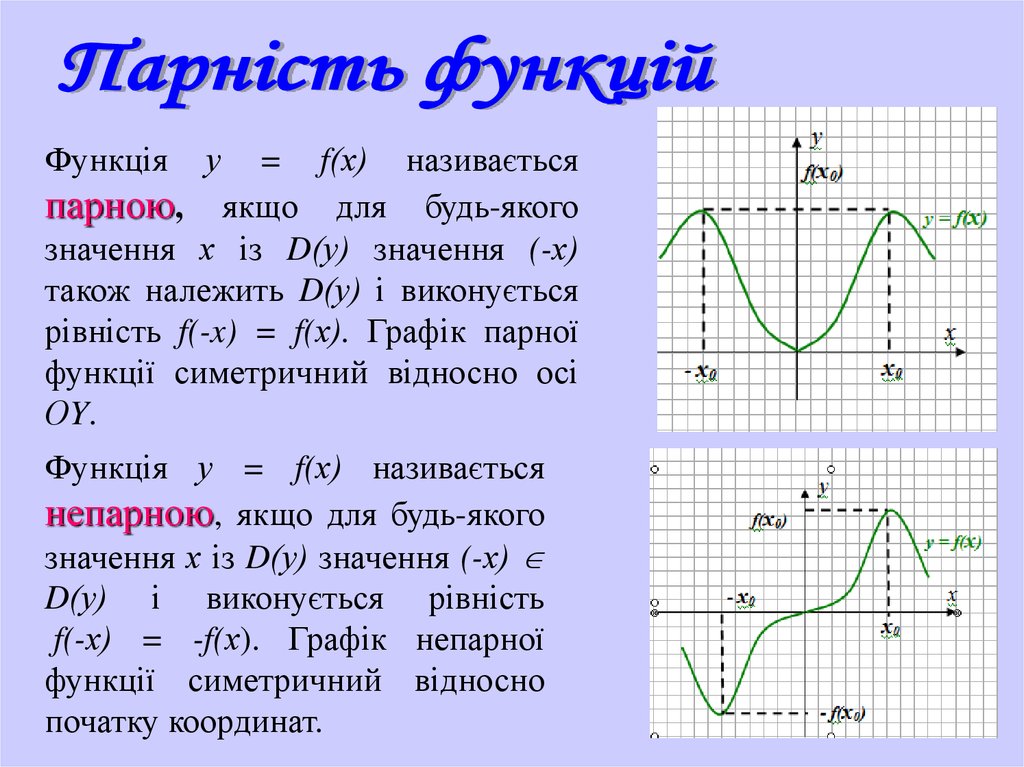
парною, якщо для будь-якого
значення х із D(у) значення (-х)
також належить D(у) і виконується
рівність f(-x) = f(х). Графік парної
функції симетричний відносно осі
ОY.
Функція у = f(х) називається
непарною, якщо для будь-якого
значення х із D(у) значення (-х)
D(у) і виконується рівність
f(-х) = -f(х). Графік непарної
функції симетричний відносно
початку координат.

15.

16.

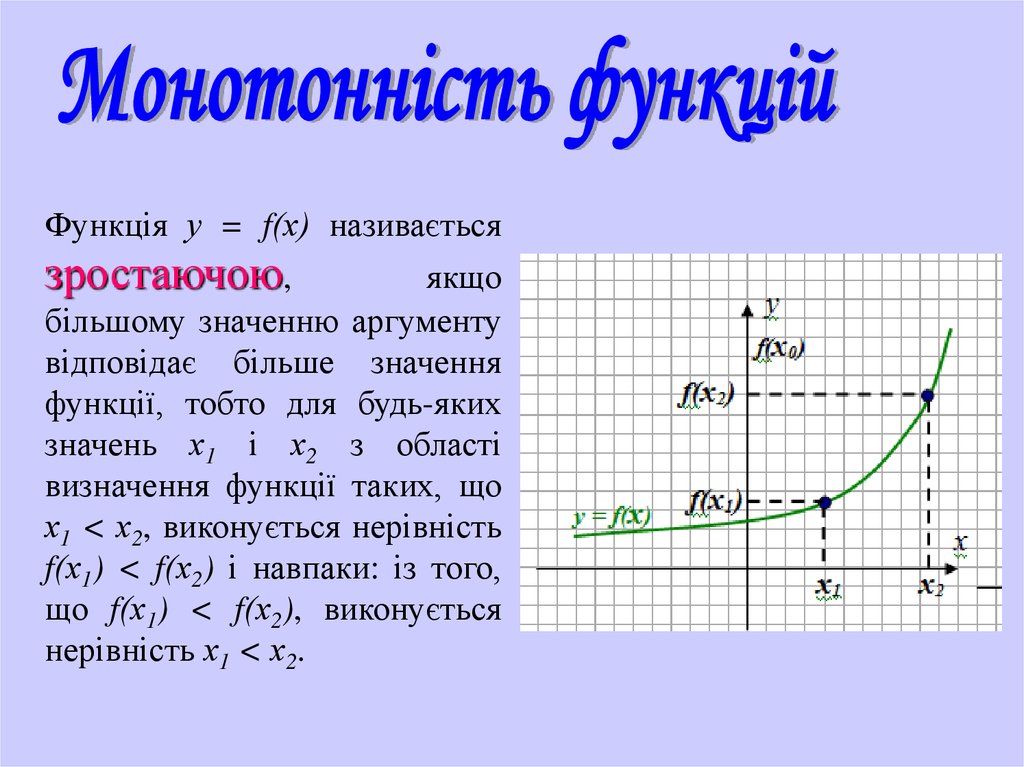
Функція у = f(х) називається
зростаючою,
якщо
більшому значенню аргументу
відповідає більше значення
функції, тобто для будь-яких
значень х1 і х2 з області
визначення функції таких, що
х1 < х2, виконується нерівність
f(х1) < f(х2) і навпаки: із того,
що f(х1) < f(х2), виконується
нерівність х1 < х2.

17.

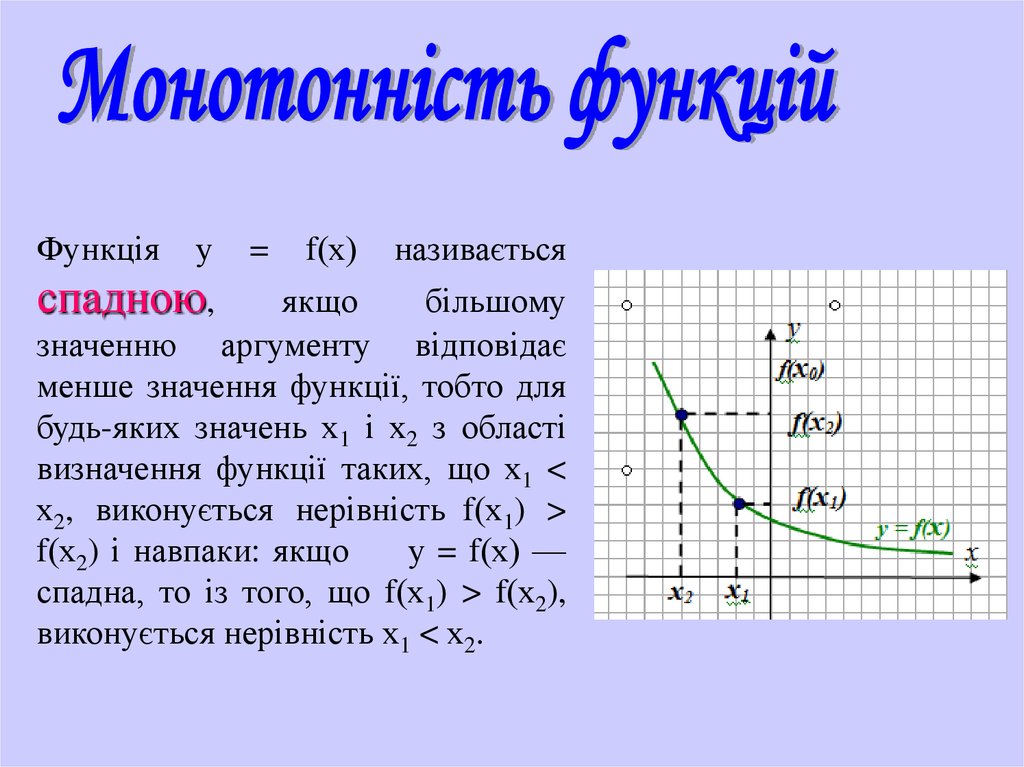
Функція
у
спадною,
=
f(х)
називається
якщо
більшому
значенню аргументу відповідає
менше значення функції, тобто для
будь-яких значень х1 і х2 з області
визначення функції таких, що х1 <
х2, виконується нерівність f(х1) >
f(х2) і навпаки: якщо
у = f(х) —
спадна, то із того, що f(х1) > f(х2),
виконується нерівність х1 < х2.

18.

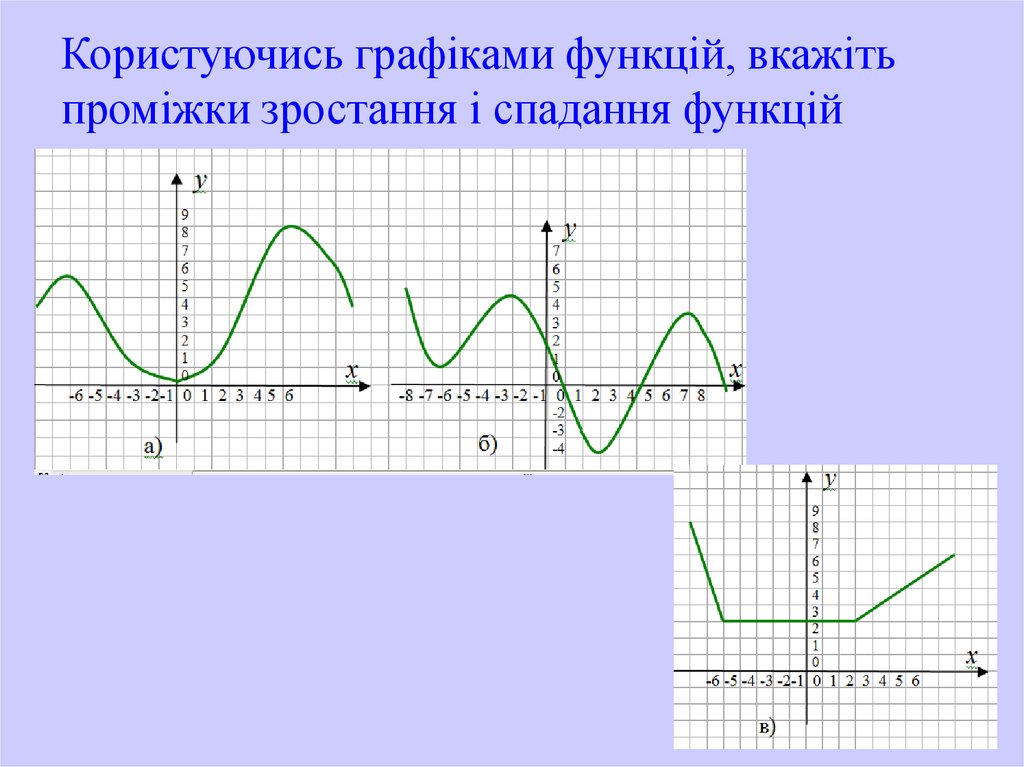
Користуючись графіками функцій, вкажіть
проміжки зростання і спадання функцій

19.

Дві
функції
f(х)
та
g(y)
називаються
взаємно
оберененими,
якщо формули у= f(х) та х= g(y)
виражають одну і ту саму залежність міжзмінними х та у:
у= f(х) х= g(y)
Функція має обернену, якщо функція строго зростає або
строго спадає (строго монотонна).
Що отримати обернену функцію від деяких функцій,
зменшують область визначення так, щоб область значень
функції не змінилася.

20.

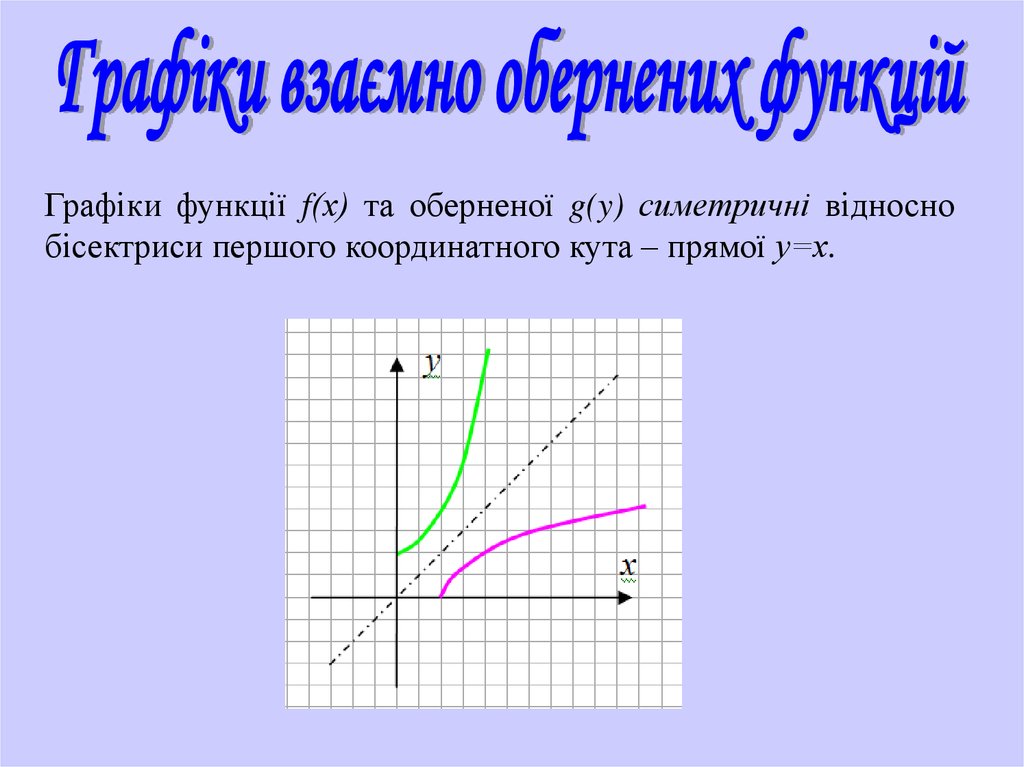
Графіки функції f(х) та оберненої g(y) симетричні відносно
бісектриси першого координатного кута – прямої у=х.

21.

Якщо f(х) та g(y) обернені функції, то область визначення
функції f(х) співпадає з областю значень функції g(y) і
навпаки.
Якщо одна з взаємно обернених функцій строго зростає, то і
друга строго зростає.

22.

функция вида y = k х
1) D( f ) = R;
2) E( f ) = R;
3) Графіком функції є
пряма лінія, яка
проходить через
початок координат.
y
x

23.

функція виду y = k х + b
1) D( f ) = R;
2) E( f ) = R;
3) графіком функції є
пряма лінія
y
k>0
k=0
x
k<0

24.

y
k
функція виду y = ;
x
1. D( f ) = (-∞;0) (0;∞)
2. E( f ) = (-∞;0) (0;∞);
3. Графіком функції є
гіпербола
k<0
k>0
x

25.

Кожному графіку поставте у
відповідність формулу:
k
y=
x
y = 2x
y
y
x
y = x²
y = 2x + 2
y
y
x
x
x

26.

Кожну пряму
співвіднесіть до її рівняння:
y x
y 2
x 2
y
y
x
y 2
y
y
x
x
x