Similar presentations:
Властивості функцій
1.
Презентація до уроку зтеми «Властивості
функцій.»
Алгебра 9 клас.
2.
Мета урокаУзагальнити та систематизувати
знання з теми «Дослідження функцій».
Задачі урока
1.Повторити схему дослідження функції.
2.Розвивати уміння застосовувати
теоретичні знання при читанні графіків
функцій різної складності.
3.Розвивати уміння розподіляти час урока,
оцінювати свою учбову діяльність.
3.
План урока.1. Самостійна робота ( читання графіків
функцій у=kх +b , у = k / х , у = х² , у = х³).
2. Повторення теорії з теми «Властивості
функцій».
x, x 0;
3. Дослідження функцій :
y= x , 0 x 4;
__
8
, x 4.
у=2|х|, у = √ х, y = |2|x| − 3| ,
x
4 . Читання складних графіків.
5 . Домашня робота.
6. Самостійна робота.
4.
Сформулюйте означення:1. Область визначення функції …
2. Область значень функції …
3. Функцію f(x) наз.зростаючою(спадною)
на проміжку L, …
4. Нулі функції …
5. Найбільше( найменше) значення
функції…
6. Функцію f(x) наз.парною (непарною), …
7. Проміжки знакосталості…
5.
Схема дослідження функції:1. Область визначення функції.
2. Область значень функції.
3. Проміжки зростання, спадання
функції.
4. Нулі функції.
5. Найбільше, найменше значення
функції.
6. Парність, непарність.
7. Проміжки знакопосталості.
?
6.
Самостійна робота №1.Побудувати графіки функцій й
записати за графіком їх властивості.
Варіант 1
Варіант 2
1) у = х + 3
1) у = −х +4
2) у= х²
2) у= х³
7.
ПЕРЕВІР СЕБЕ( взаємоперевірка, робота в парах)
8.
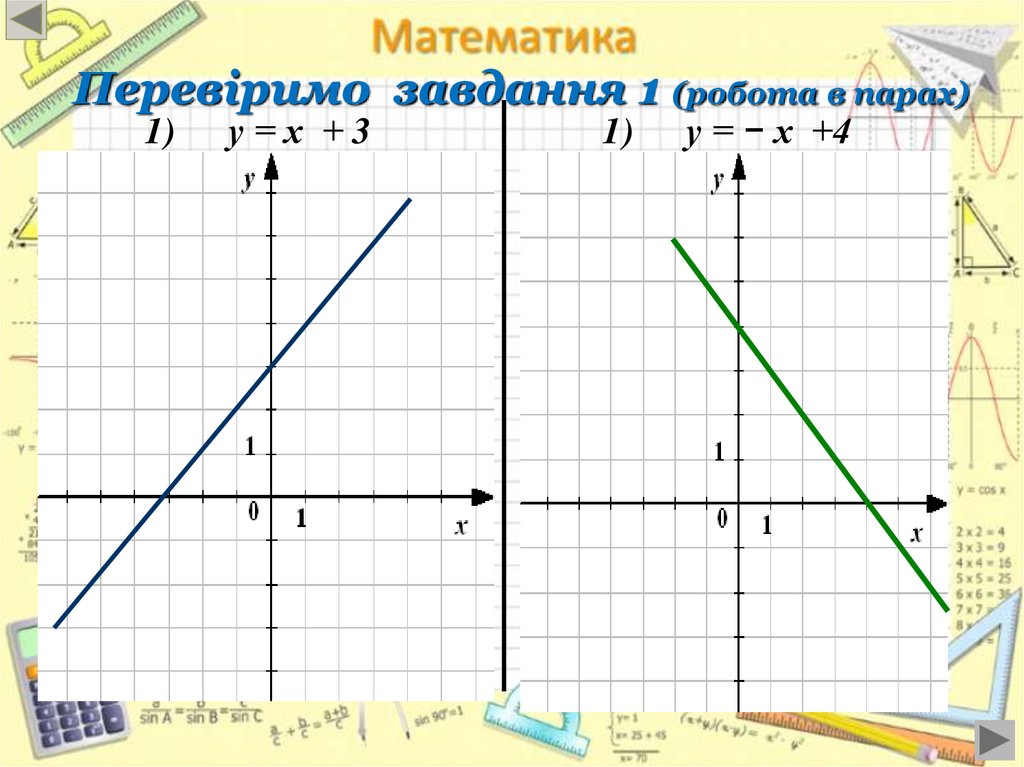
Перевіримо завдання 1 (робота в парах)1)
у=х +3
1)
у = − х +4
9.
у= х+3у=−х+4
1. D ( y ) ; .
1. D ( у ) ; .
2. E ( у ) ; .
2. E ( у ) ; .
3. у=0 при х=−3.
3. у=0 при х=4.
4. у>0, якщо х 3 ; , 4.у>0, якщо х ;4 ,
у<0, якщо х ; 3 .
5. Функція зростає
на
(−∞ ; +∞).
6. унайм.= немає;
унайб.= немає.
у<0, якщо х 4; .
5. Функція спадає на (−∞;+∞).
6. унайм.= немає,
Унайб.= немає.
7. Неперервна.
7. Неперервна.
8. Ні парна ні непарна
8. Ні парна ні непарна
(індиферентна).
(індиферентна).
10.
Перевіримо завдання 2(робота в парах).
Побудувати графіки функцій та
записати за графіком їх властивості.
2) у= х²
2) у= х³
11.
у= х²у=х³
12.
у= х²1. D ( у ) ; .
2. E ( у ) 0 ; .
3. у=0, якщо х= 0.
4. у>0,якщо
x ;0 0; .
функ.сп.на
;0 .
6. унайм.= 0,
якщох=0.
5.Функ.зр.на 0 ; ,
у=х³
1. D ( y ) ; .
2. E ( y ) ; .
3. у=0 якщо х=0.
4. у>0, якщо x 0 ; ,
x ; 0 ; .
у<0, якщо
5. Функ. зр.на ; .
6. унайм.= немає, унайб.= немає.
7. Неперервна.
7. Неперервна.
8.у=0 —вісь симетрії
9 . Функція симетрична
відносно початку координат,
функція непарна
графіка, ф-ція парна.
13.
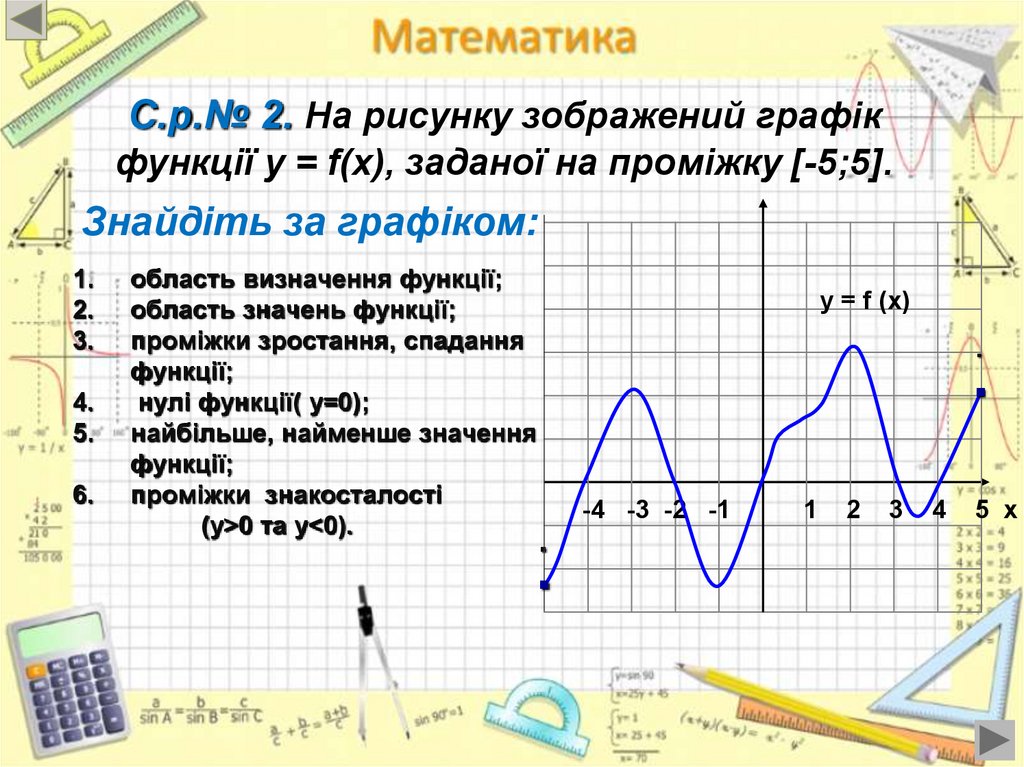
С.р.№ 2. На рисунку зображений графікфункції у = f(x), заданої на проміжку [-5;5].
Знайдіть за графіком:
1.
2.
3.
4.
5.
6.
область визначення функції;
область значень функції;
проміжки зростання, спадання
функції;
нулі функції( у=0);
найбільше, найменше значення
функції;
проміжки знакосталості
(у>0 та у<0).
y = f (x)
.
.
-4 -3 -2 -1
.
.
1
2
3
4
5 х
14.
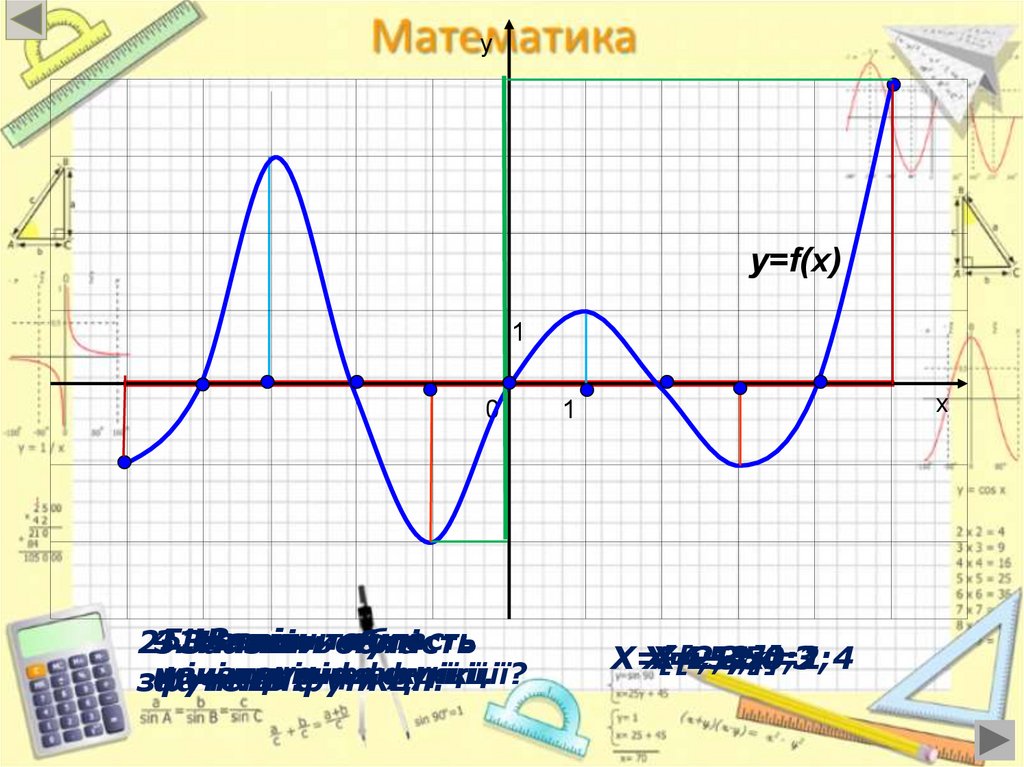
На рисунку зображений графік функції у = f(x),заданої на проміжку [-5;5].
2. E ( y ) 2,5; 3 .
1.
D ( y ) 5 5; .
3. у=0, якщо х =−4;−2;0;3;4.
4.у>0, якщо x 4 ; 2 0 ;3 4;5 ,
у<0, якщо
y = f (x)
x 5; 4 2 ;0 3; 4 .
..
5. Функція зростає
на 5 ; 3 , на 1;2 , на 3,5 ; 5
Функція спадає
на 3 ; 1 , на 2;3,5 .
6. унайм.=−2,5 ; унайб.= 3
7. Функція неперервна.
1
2
3
-4 -3 -2 -1
.
9. Ні парна ,ні непарна
(індиферентна)
4
5 х
15.
С.р.№ 3. Математичний мінідиктант.На рисунку изображений графік
функції у = f (x),
заданої на проміжку [-5;5].
Дайте відповідь на запитання
Уважно, швидко, вірно запишіть відповіді.
16.
На рисунку зображений графік функції у =f (x), щозадана на проміжку [-5;5]. Дай письмову відповідь
на питання.
у
1. Запишіть область
визначення функції.
y=f(x)
2. Запишіть область
значень функції.
3. Назвіть нулі
функції.
4.Назвіть точки
максимумів функції.
5.Назвіть точки
мінімумів функції.
1
0
1
х
17.
ПЕРЕВІР роботу сусіда.(робота в парах)
18.
уy=f(x)
1
0
4.
5.Назвіть
1.Запиши
Назвіть
область
2.
3.
Запиши
Назвітьточки
область
нулі
максимумів
мінімумів
визначення
функції.
функції.
функції?
значень
функції.
функції.
х
1
Х=-4;-2;0;2;4
Х=-1;х=3
Х=-3;х=1
[-2;4]
[-5;5]
19.
С.р.№ 4. Побудуйте графік функції тазапишіть за графіком :
Варіант1
1. D(у).
2. Е(у).
3. у>0.
4. у<0.
5. у=0.
y = 2|x|
Варіант2
y = |2|x| - 3|
Варіант3
6.унайменше
y=
x , x 0;
x , 0 x 4;
8
, x 4.
x
20.
y = 2|x|ПЕРЕВІР СЕБЕ. Варіант1.
1. D(у)= R.
2.
Е(у)=[0;∞).
3. у>0 якщо хЄ R, окрім х=0.
4. У<0, немає.
5. у=0, якщо х=0.
6. унайм.=0, якщо х = 0.
21.
2) y = |2|x| - 3|ПЕРЕВІР СЕБЯ. Варіант 2.
Побудова:
а) Графік y = 2x – 3 для x>0.
б) Графік y = – 2x – 3 для x<0.
в) Ламана симетрична
відносно вісі Oу.
1. D(у)= R
2. Е(у)=[0;∞)
3 .у>0 при х Є R,окрім х=±1,5.
4. У<0, немає.
5. У = 0, якщо х=±1,5.
6. унайм.=0, якщо х= ±1,5.
22.
ПЕРЕВІР СЕБЕ. Варіант 3.Нарисуйте схематично графік функції
x, x 0;
y=
х , 0 x 4;
8
, x 4.
x
1.
2.
Та запишіть за графіком : 3.
4.
5.
D(у)
Е(у)
у>0,
у<0
у=0
6. у найменше.
23.
yy
y
1
2
2
1
1
1
-1
0
x
-1
0 1
-1
4 x
1. у x, x 0 2. у х , 0 x 4
y=
x, x 0;
х , 0 x 4;
8
, x 4.
x
0 1
3. у
y
4
x
8
,x 4
x
2
1
-1
0
-1
4
x
24.
ПЕРЕВІР СЕБЕ:1. D ( y ) ;
2. E ( y ) 0;
3. у>0, якщо хЄ(−∞ ;0)U (0 ;+∞)
4. У<0, немає
y
5. у=0, якщо х=0.
6. унайм.=0, якщо х=0.
2
1
-1
0
-1
4
x
25.
Додому:§ ____ №_______________;
Побудуйте графіки функцій
та запишіть їх властивості
у=…
у=…
у=…
26.
Самостійна робота № 5( 10 хв.)
27.
1.Прочитати графік (за схемою).Варіант 1
Варіант 2
9
У
9
4
1
4
-1
1 2 3
Х
1
-1
1 2 3
Х
2.Побудуйте графік функції.
у
8
x
2.Побудуйте графік функції.
у x
Дайте відповіді на питання, користуючись графіком:
а) найбільше та найменше значення функції;
б )при яких значеннях х функція додатна, дорівнює нулю;
в) координати точок перетину з віссю у.
28.
Додатково: 1) укажіть проміжки зростання, спадання, точкимаксимума та мінімума.
Варіант 1
.
у
y=f(x)
у
y=f(x)
.
1
0
Варіант 2
1
1
х
0
1
х
29.
Якщо залишився час,повторити:
1)схему дослідження функції;
2) перевірити додаткове завдання
самостійної роботи.
30.
1.D ( y ) 4;0 0;4 . На рисунку зображений графік
функції у = f(x), дайте відповдь на
2. E ( y ) 3; 1 1; 3 . .
запитання,коистуючись графіком .
3. у=0, немає
4. у>0, якщо
у<0, якщо х 4 ; 0 .
х 0 ; 4 ,
у
y=f(x)
5. Функція спадає
на 4 ; 3 на 1;0 на 0 ;1 на 3 ;4
Функція зростає
на 3 ; 1 на 1;3 .
6. унайм.=−3; у найб =3.
7. Розривна в точці х=0.
8. Непарна.
1
0
1
х
31.
На рисунку зображений графік1. D ( у ) 3,8 ;0 . функції у = f(x), дайте відповдь на
2. E ( у ) 3,7 ; 4,2 . запитання,коистуючись графіком.
3. у=0, якщо х=−3;−1,2.
.
4. у>0, якщо х 3,8; 3 1,2; 0 ,
у<0,якщо х 3; 1,2 .
5. Функція спадає
на 3,8 ; 2 , на 0,7;0 .
6.Функція зростає
на 2 ; 0,7 .
7. унайм.=−3,8; у найб = 4,2.
8.Неперевна.
9. Ні парна ,ні непарна
(індиферентна).
у
y=f(x)
.
1
0
1
х






























 mathematics
mathematics








