Similar presentations:
Логарифмічна функція
1.
Логарифмічнафункція, її графіки
та властивості
2.
Функція у=ах (a>0 , a 1) при:a >1 монотонно зростає на R ;
0<a<1 монотонно спадає на R.
У
У
y = аx
у
a >1
у
0
0<a<1
1
1
1х
Х
х
0
1
Кожному значенню x з області визначення функції відповідає
єдине значення у з області значенння цієї функції.
Х
3.
Функція у=ах (a>0 , a 1) при:a >1 монотонно зростає на R ;
0<a<1 монотонно спадає на R.
У
У
y = аx
у
a >1
у
0
0<a<1
1
1
1х
Х
х
0
1
Х
Кожному значеннню у з області значення функції відповідає
єдине значення х з області визначення цієї функції.
4.
Нехай маємо функцію у=ах , а>0, a 1.Поміняємо місцями х і у. Дістанемо: х=ау .
За означенням логарифма: y=logaх.
Означення:
Функцію, яку можна задати формулою
y = logax ( а 0, а 1 ),
називають логарифмічною функцією.
5.
При(a 0, a 1)
g(x)=ax
f(x)= logax
D(g)=R
D(f)=(0; )
E(g)=(0; )
E(f)=R
За означенням функції
g(x)=ax, a 0, a 1 и f(x)=log ax, a 0, a 1
є взаємно оберненими
6.
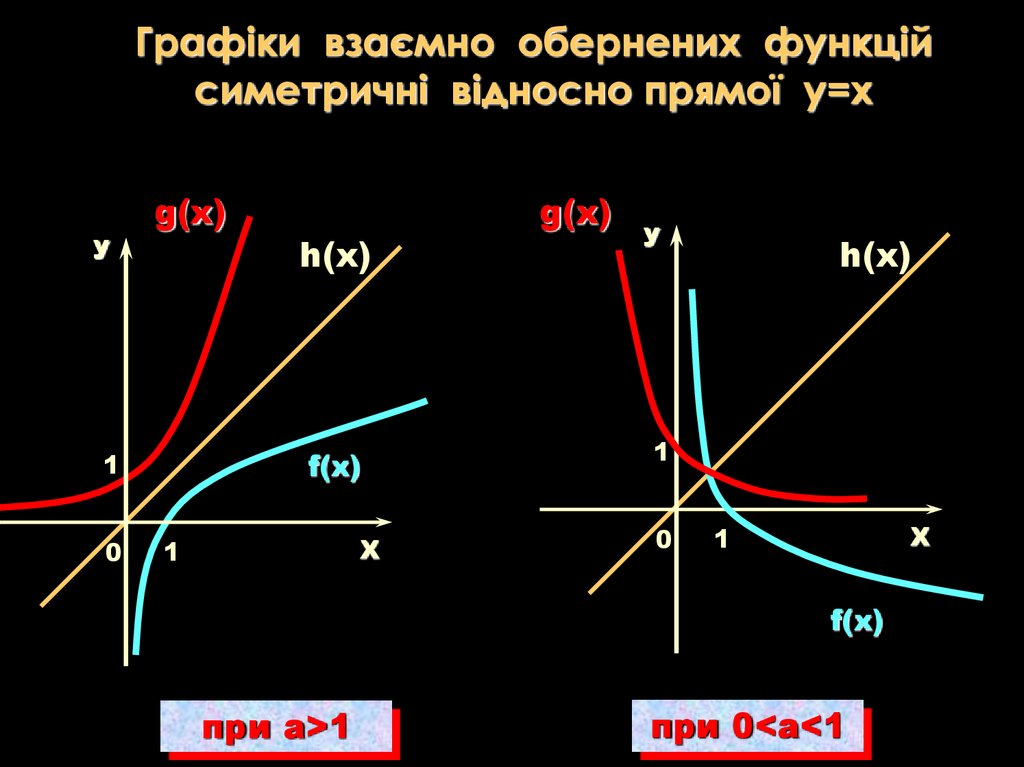
Графіки взаємно обернених функційсиметричні відносно прямої у=x
У
g(x)
f(x)
1
0
h(x)
Х
1
g(x)
У
h(x)
1
0
Х
1
f(x)
при a>1
при 0<a<1
7.
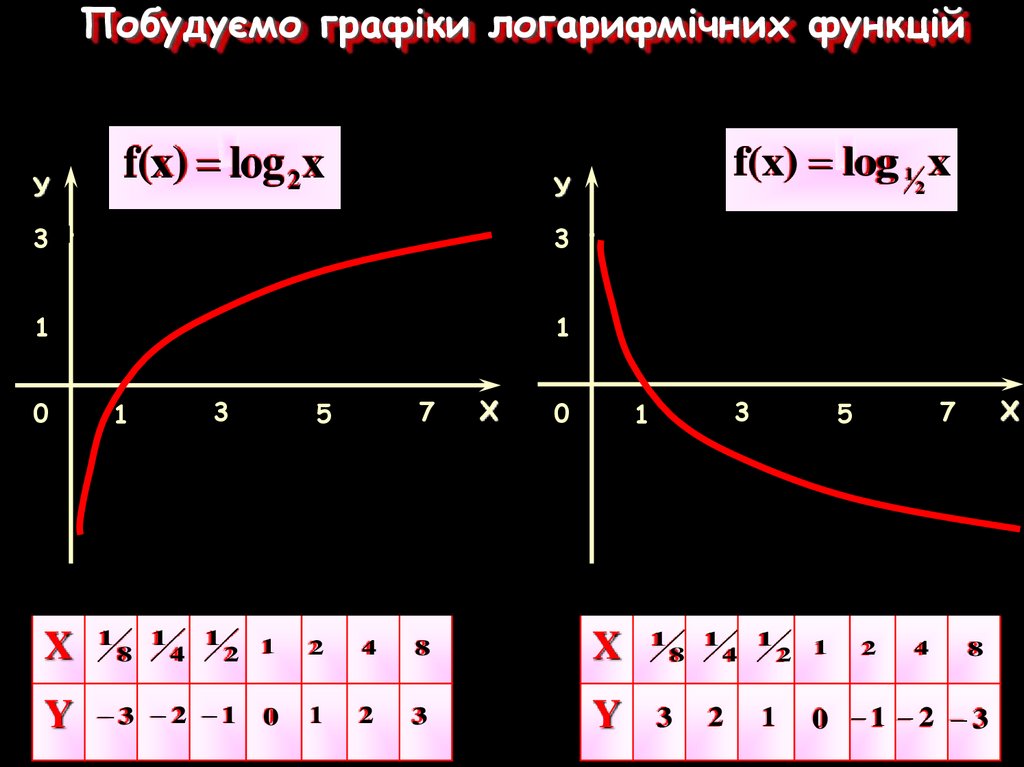
Побудуємо графіки логарифмічних функційУ
f(x) log 2 x
3
3
1
1
0
1
3
f(x) log 1 2 x
У
7
5
Х
0
3
1
X 18 14 12 1
2
4
8
X
1
Y 3 2 1 0
1
2
3
Y
3
8
1
4
2
1
1
2
1
Х
7
5
2
4
8
0 1 2 3
8.
Властивості функції1.
при a>1
при 0<a<1
(0; ∞);
Область визначення
R
2. Область значень
3. Парність, непарність
Є ні парною, ні непарною
4. Нулі функції
5. Проміжки
знакосталості:
6. Екстремуми
Проміжки монотон7. ності при x (0; ):
8. Асимптота
y=0 при x=1
y>0 при x (1; );
y<0 при x (0;1);
немає
Функція
зростає
Функція
спадає
x=0
У
У
0
y>0 при x (0;1);
y<0 при x (1; );
1
Х
a>1
y = logаx ,
0
1
Х
0<a<1
9.
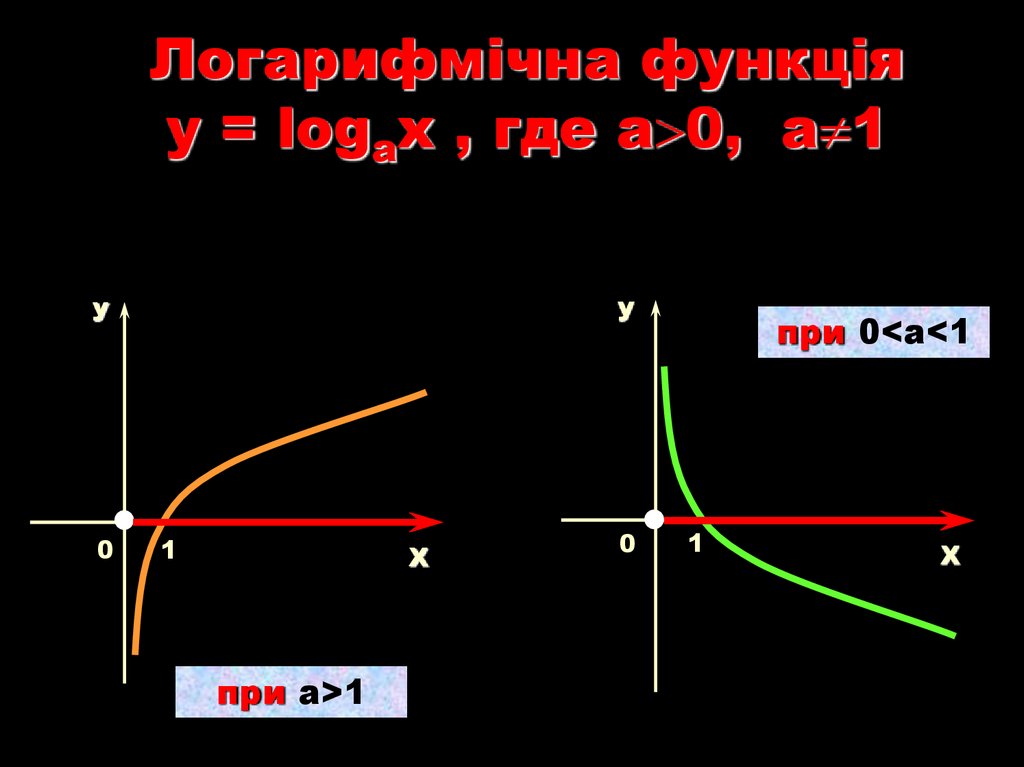
Логарифмічна функціяy = logаx , где а 0, а 1
У
У
0
1
Х
при a>1
0
при 0<a<1
1
Х
10.
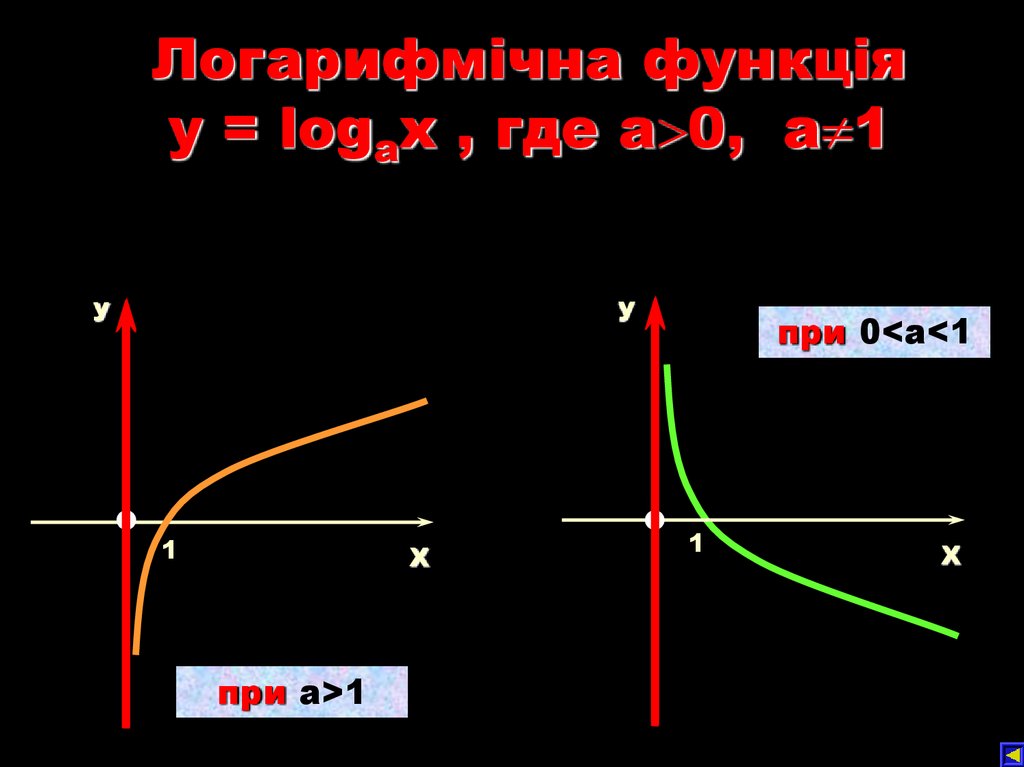
Логарифмічна функціяy = logаx , где а 0, а 1
У
У
1
Х
при a>1
при 0<a<1
1
Х
11.
Логарифмічна функціяy = logаx, при a>1
У
0
Х
1
у >0
при х 1;
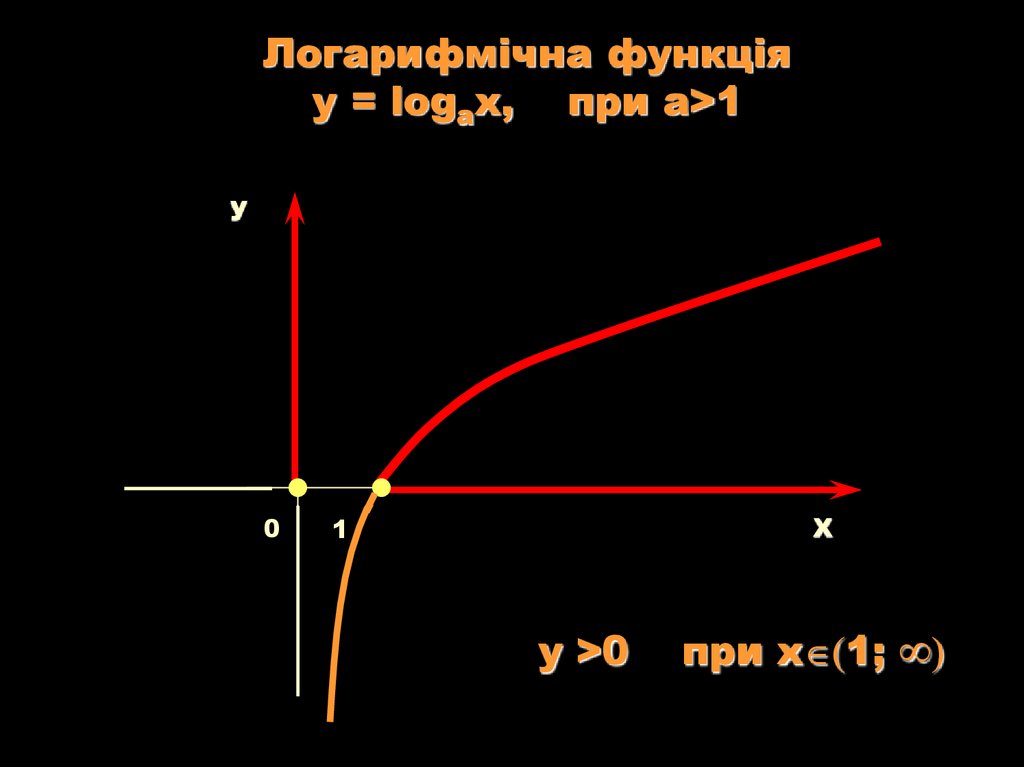
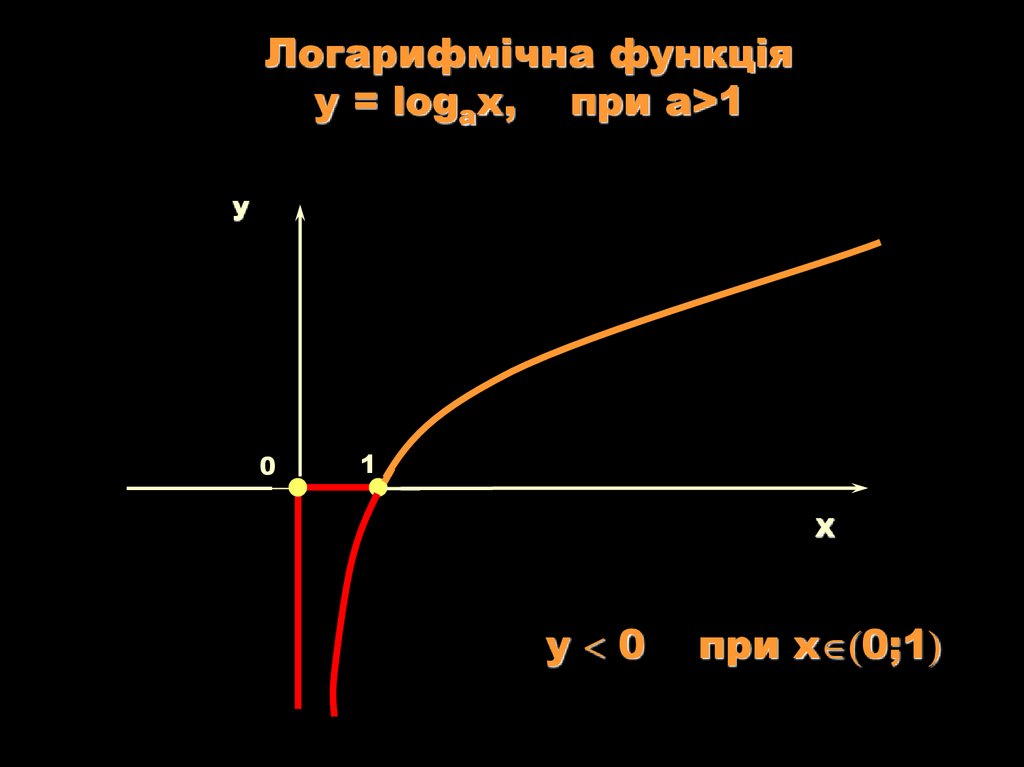
12.
Логарифмічна функціяy = logаx, при a>1
У
0
1
Х
у 0
при х 0;1
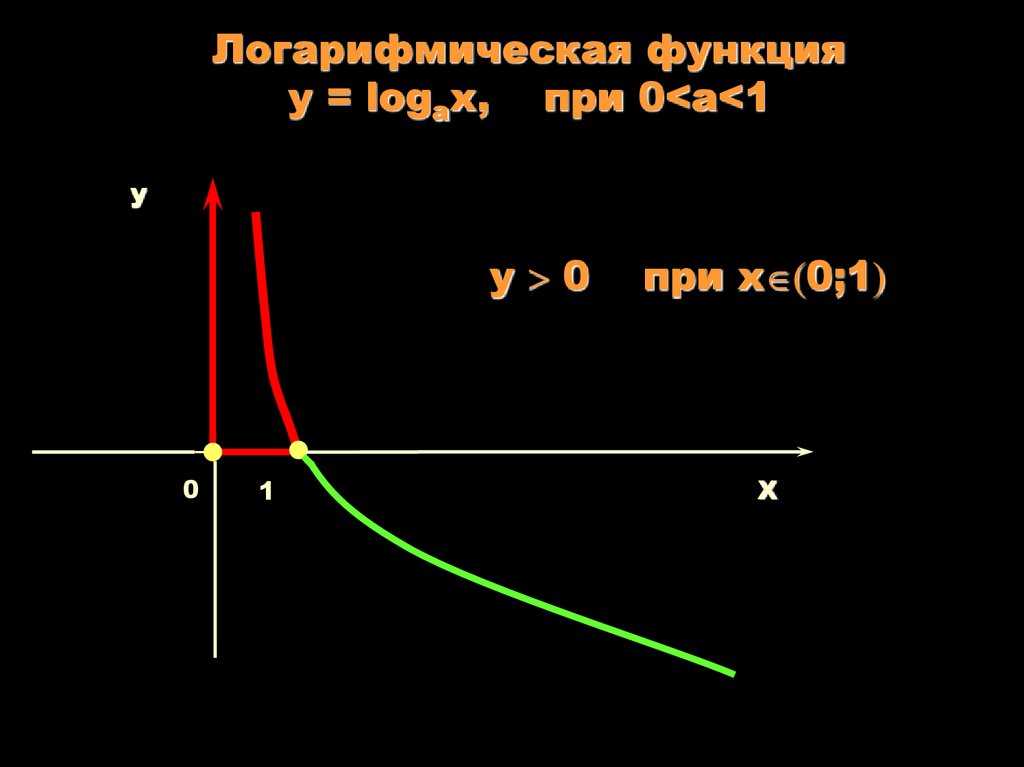
13.
Логарифмическая функцияy = logаx, при 0<a<1
У
у 0
0
1
при х 0;1
Х
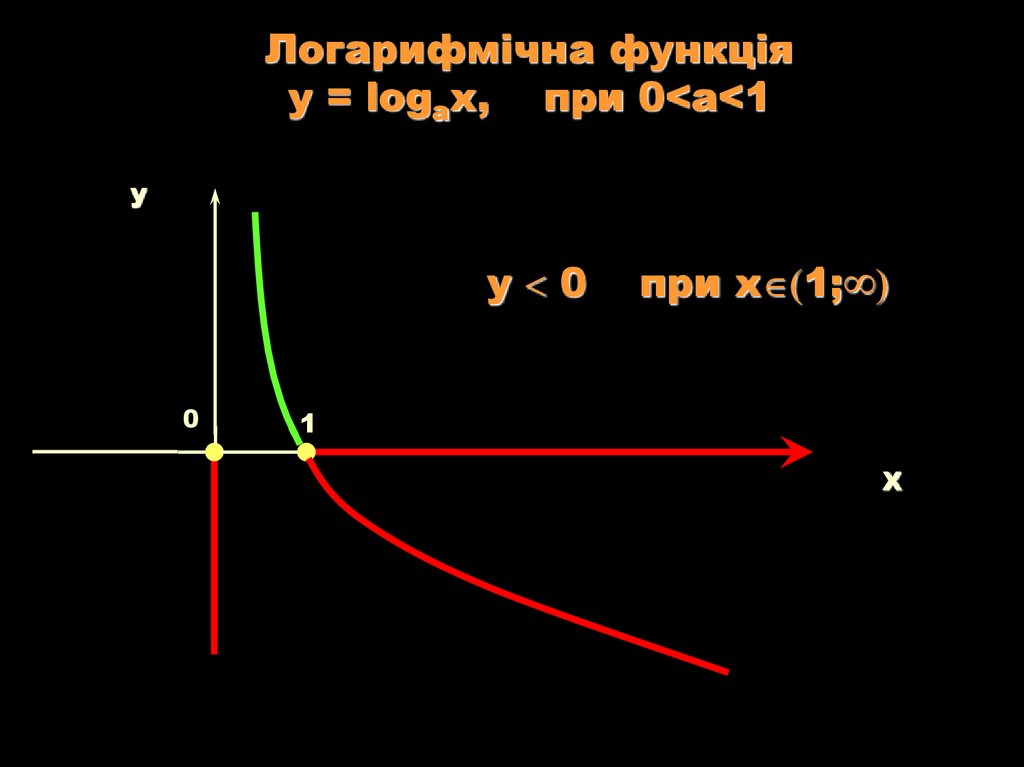
14.
Логарифмічна функціяy = logаx, при 0<a<1
У
у 0
0
при х 1;
1
Х
15.
Логарифмічна функціяy = logаx, при a>1
У
y2
y1
0
1
x1
x2
Х
16.
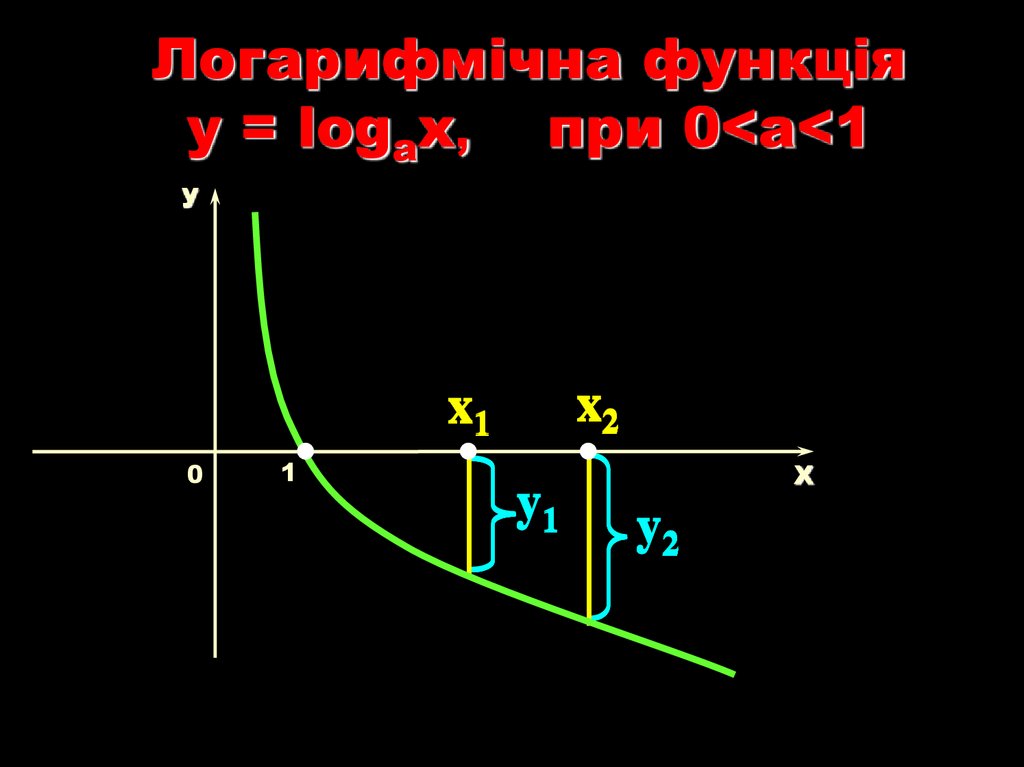
Логарифмічна функціяy = logаx, при 0<a<1
У
x2
x1
0
1
y1
Х
y2
17.
Які з нижче перерахованих функцій єзростаючими, а які спадними?
y log 2 x
зростаюча,
2 1
спадна,
0 0,5 1
y lg x
зростаюча,
10 1
y lnx 2
зростаюча,
e 1
спадна,
0 0,7 1
y log 0,5 x
2
y log 0,7 x 4
18.
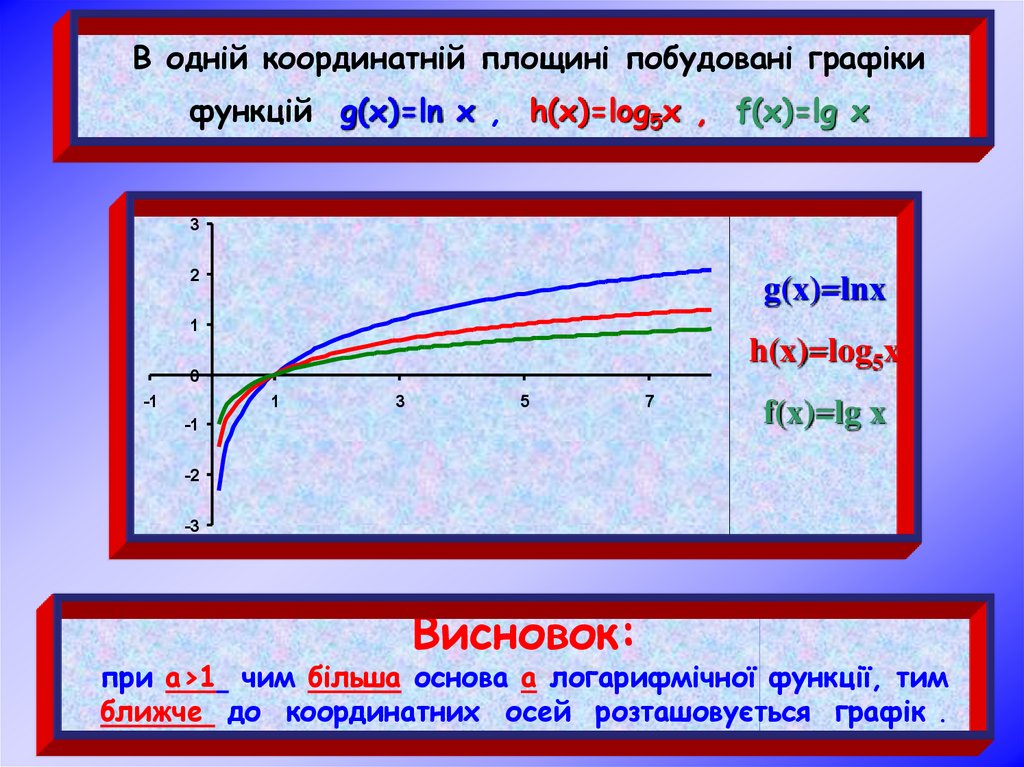
В одній координатній площині побудовані графікифункцій g(x)=ln x , h(x)=log5x , f(x)=lg x
3
2
g(x)=lnx
1
h(x)=log5x
0
-1
1
3
5
-1
7
f(x)=lg x
-2
-3
Висновок:
при а>1 чим більша основа а логарифмічної функції, тим
ближче до координатних осей розташовується графік .
19.
В одній координатній площині побудовані графікифункцій
g(x)=log0,1x,
h(x)=log0,3x,
f(x)=log0,5x
4
3
2
1
g(x)=log0,1x
0
-1
-1
1
3
5
7
-2
h(x)=log0,3x
f(x)=log0,5x
-3
-4
Висновок:
при 0<а<1 чим більша основа а логарифмічної функції,тим
далі від осей координат розташовується графік .









 mathematics
mathematics








