Similar presentations:
Розв’язування логарифмічних рівнянь
1. Розв’язування логарифмічних рівнянь
Успіху!log 2 16
g ( x) 2
log2 ( x 3)
Розв’язування
логарифмічних
рівнянь
2.
Існують основні методи розв’язуваннялогарифмічних рівнянь:
Метод введення нової змінної;
Метод потенціювання;
Метод логарифмування;
Функціонально – графічний метод;
3.
Нехай log 2 x a; a 2 4a 3 0,log 32 x 4 log 3 x 3
a 1 4; a 2 1.
звідси log 2 x 4, тому х 16;
log 2 x 1, х 0,5. Відповідь :16; 0, 5.
log 5 ( x 1) log 5 ( x 2) log 5 ( x 2)
Пропотенціюємо дану рівність і
одержимо:
log5( x-1)( x-2) = log5( x+2);
x2-4x=0; х=0, х=4.
Враховуючи ОДЗ: х-1>0,
х-2>0,
х+2>0;
хЄ(2; )
Відповідь: 4.
4.
log 3 х 2log 1 x 3 ОДЗ : х. 0log 3 x
log 3 х 2
3;
1
log 3
3
Відповідь : Х 3.
3
log 3 x 2 log 3 x 3; 3log 3 x 3; x 3.
x
lgx
100 x.
ОДЗ : х. 0
Прологарифмуємо обидві частини рівняння (х 0): lgx lgx lg 100 x
.Одержимо lg x lg x lg 100 lg x; lg 2 x lg x 2 0.
Замінемо : lgx a, тому а 2 а 2 0. а1 2; а 2 1.
Тоді : 1)lgx 2; x 10 2 , x 100.
2)lgx -1: x 10 -1 , x 0,1.
Відповідь : 100; 0,1.
5.
Розв’язати рівняння функціонально– графічним методом;
y
0
log2(x + 2) – 1 x 2 2
x
1
x=-1
6.
.y
Подумай!
-0
-1
2
1
Подумай
!
Подумай!
y=1-x
y=lgx
1
-1 0
1
x
Вірно!
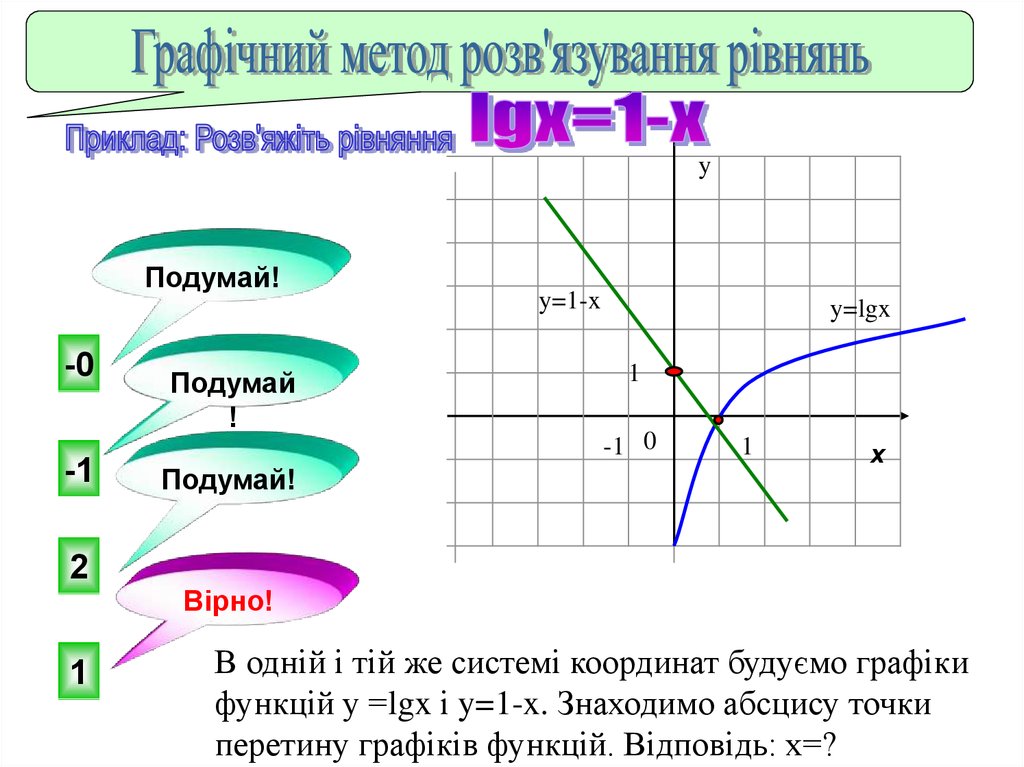
В одній і тій же системі координат будуємо графіки
функцій у =lgx і y=1-x. Знаходимо абсцису точки
перетину графіків функцій. Відповідь: х=?
7. Домашнє завданння:
1. Зробити конспект лекції.2.
3. Виконати індивідуальні завдання








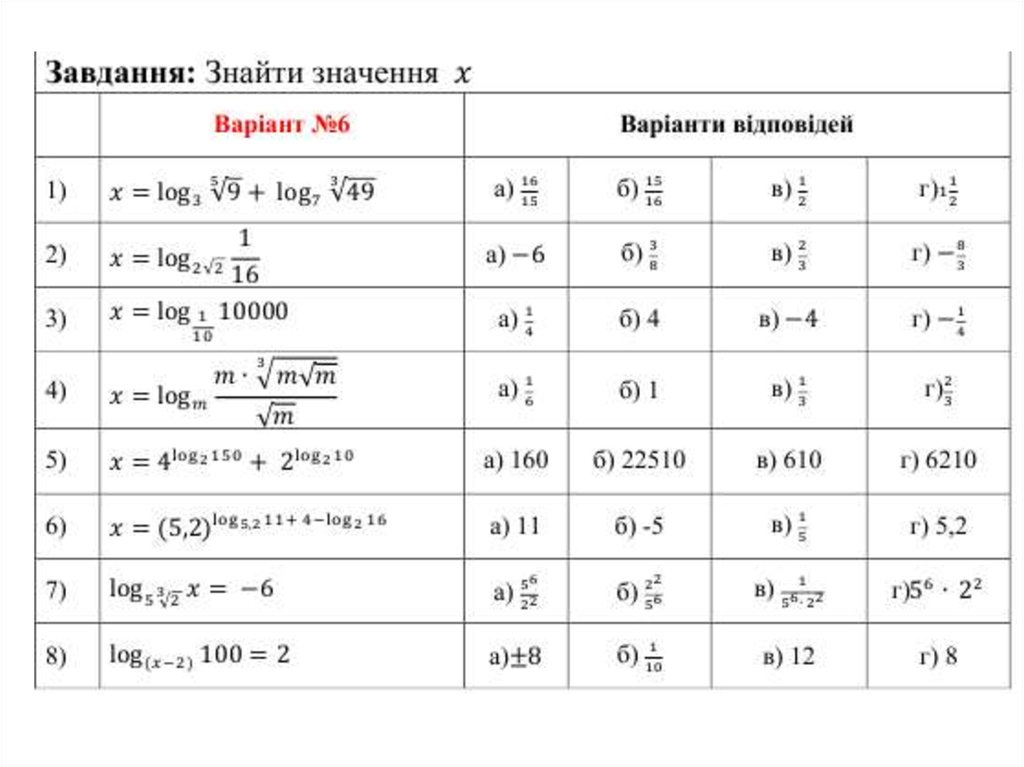

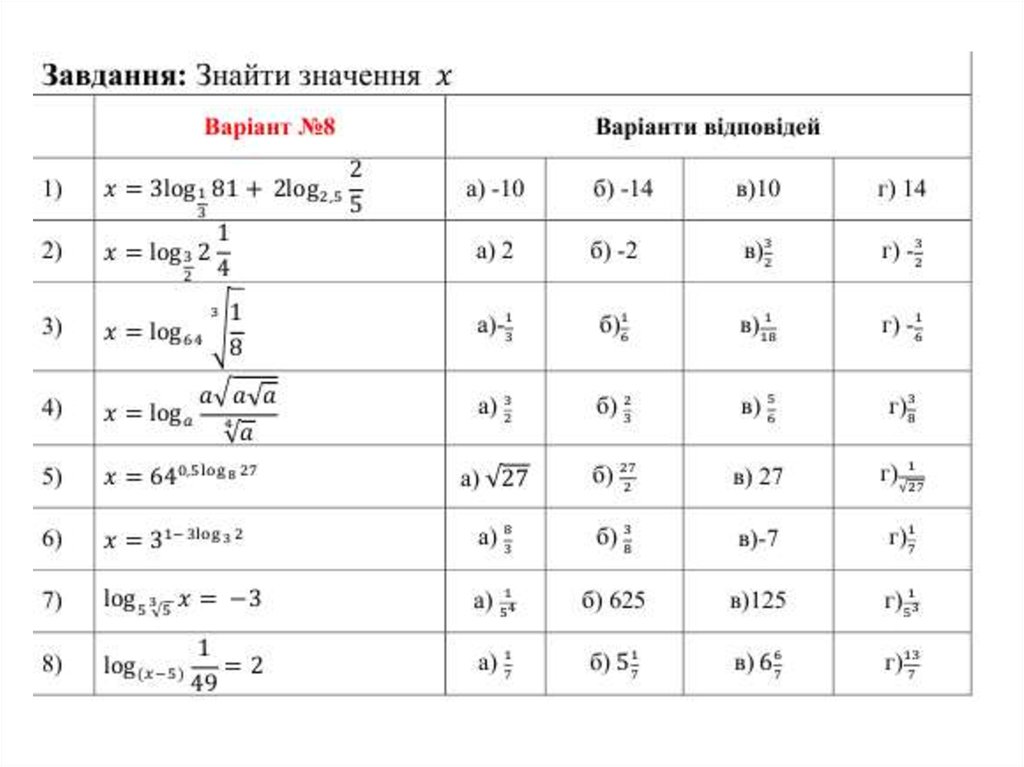

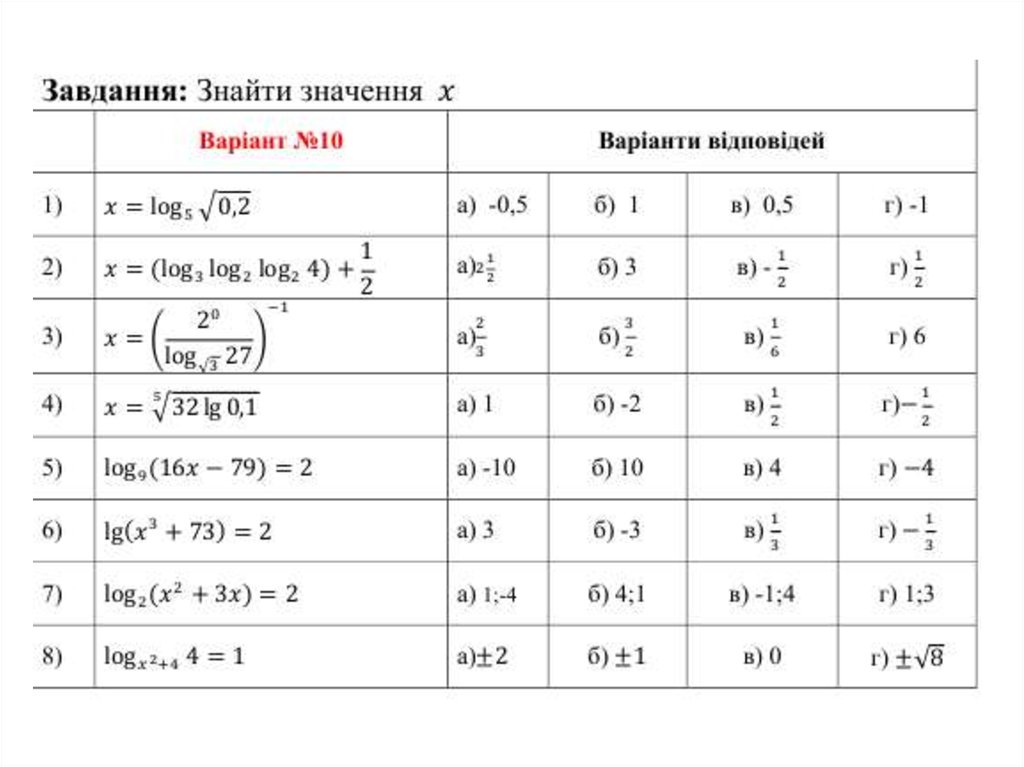
 mathematics
mathematics








