Розв’язування логарифмічних рівнянь

1. Розв’язування логарифмічних рівнянь

Успіху!
log 2 16
g ( x) 2
log2 ( x 3)
Розв’язування
логарифмічних
рівнянь

2.

Логарифмічними рівняннями
називаються рівняння, які містять
змінну під знаком логарифма
1)
log 2 х 5 9
2)
log 0,5 0,25 4 х 2 0
3)
log 3 27 2 х 4 5
4)
log 2 х log 22 х 5 9

3.

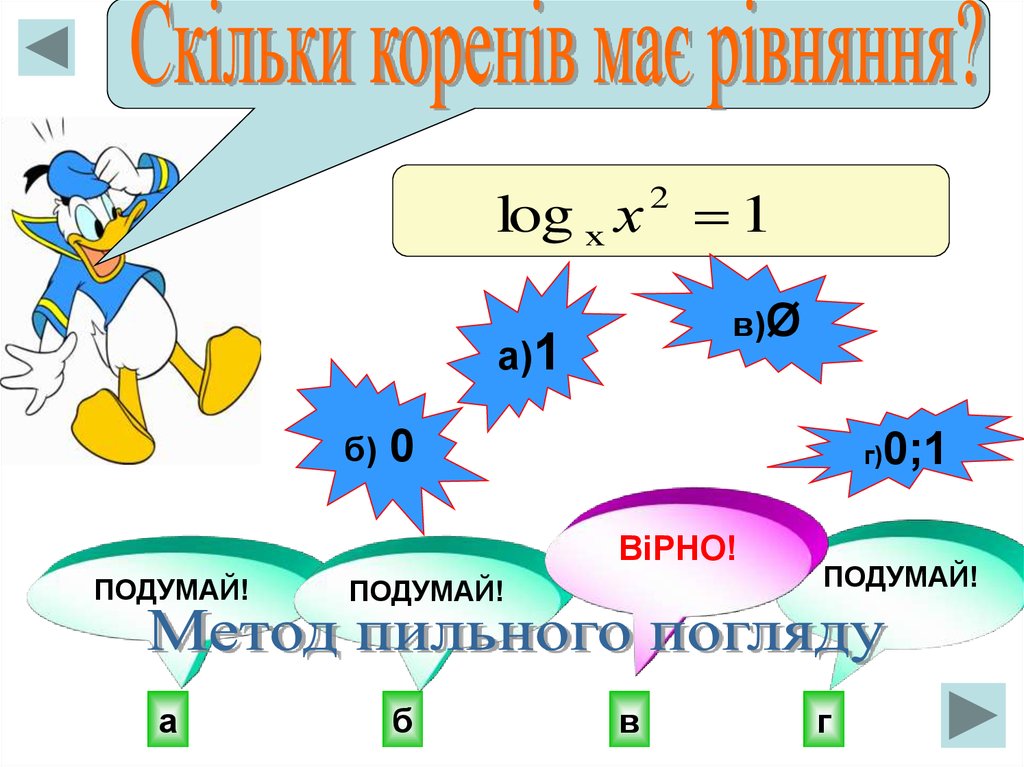
log х х 1
2
в)Ø
а)1
б)
0
г)
ВіРНО!
ПОДУМАЙ!
а
ПОДУМАЙ!
б
в
0;1
ПОДУМАЙ!
г

4.

Розв’язати логарифмічне рівняння – це означає знайти
всі його корені або довести, що рівняння коренів не має.
Найпростіші логарифмічні рівняння мають вигляд:
1
log a x b , де , а 0, а 1, х 0. За означенням х а в
2
log a x log a b, де а 0, а 1, x 0, b 0
x b.
3
log x a b, де а 0, x 1, x 0,
x a, звідси x a .
b
1
b

5. Розв'яжіть рівняння log3 (2x + 1) = 2.

Розв'язання
За означенням логарифма маємо:
2х + 1 = 32,
2х = 8,
х = 4.
Перевірка: log3(2 · 4 + 1) = log39 = 2.
Відповідь: 4.

6. Розв'яжіть рівняння log3x = log3(6 – х2).

Розв'язання
Із рівності логарифмів чисел випливає:
х = 6 – х2;
х2 + х – 6 = 0;
х1 = -3, х2 = 2.
Перевірка:
Число -3 не є коренем даного рівняння, бо вираз
log3(-3) — не визначений;
log3x = log32;
log3(6 – х2) = log3(6 – 22) = log32.
• Відповідь: 2.

7. Розв'яжіть рівняння logх+1 (2х2 + 1) = 2.

Розв'язання
За означенням логарифма маємо:
2х2 + 1 = (х + 1)2;
2х2 + 1 = х2 + 2х + 1;
х2 – 2х = 0;
х1 = 0, х2 = 2.
Перевірка:
• 1) Значення х1 = 0 не є коренем даного рівняння,
оскільки основа логарифма х + 1 не повинна
дорівнювати 1.
• 2) logх+1(2·22 + l) = log39 = 2.
• Відповідь: 2.

8.

1)
log 3 (2 x 1) 2
Х=4
2)
log 5 (6 x 2 ) log 5 x
Х=2
3)
log x 1 (2 x 1) 2
Х=2
log x 64 6
Х=2
log x 5 1
Х=0,2
4)
5)
2

9.

1) log 5 x 0;
1) х 1
2) log 3 3 4;
2) х 4
3) log 3 x 1 0;
3) х 3
4) log 2 (2 x 1) 3;
4) х 4,5
5) log 3 (2 x 3) 1 0;
5) х 3
6) log 5 (2 x x ) 0;
6)
7) log 0,7 (2 x 1) log 0,7 ( x 1).
7) х 2
2
x
2
х 1

10. Домашнє завданння:

1. Зробити конспект лекції.
2. Виконати завдання за варіантами (варіанти по стовпчиках):