Розв’язування логарифмічних рівнянь. 11 клас

1. Розв’язування логарифмічних рівнянь

Успіху!
log 2 16
g ( x) 2
log2 ( x 3)
Розв’язування
логарифмічних
рівнянь

2.

3.

Логарифмічними рівняннями
називаються рівняння, які містять
змінну під знаком логарифма
1)
log 2 х 5 9
2)
log 0,5 0,25 4 х 2 0
3)
log 3 27 2 х 4 5
4)
log 2 х log 22 х 5 9

4.

1)
sinх log 2 32
2)
log 5 х log 1 ( х 1) 0
5
3)
2 х
1
log 2
4

5.

log х х 1
2
в)Ø
а)1
б) 0
г)
ВіРНО!
ПОДУМАЙ!
а
ПОДУМАЙ!
б
в
0;1
ПОДУМАЙ!
г

6.

Розв’язати логарифмічне рівняння – це означає знайти
всі його корені або довести, що рівняння коренів не має.
Найпростіші логарифмічні рівняння мають вигляд:
1
log a x b , де , а 0, а 1, х 0. За означенням х а в
2
log a x log a b, де а 0, а 1, x 0, b 0
x b.
3
log x a b, де а 0, x 1, x 0,
x a, звідси x a .
b
1
b

7.

1)
log 3 (2 x 1) 2
Х=4
2)
log 5 (6 x 2 ) log 5 x
Х=2
3)
2
log x 1 (2 x 1) 2
Х=2
4)
log x 64 6
Х=2
5)
log x 5 1
Х=0,2

8.

Існують основні методи розв’язування
логарифмічних рівнянь:
Метод введення нової змінної;
Метод потенціювання;
Метод логарифмування;
Функціонально – графічний метод;
Метод пильного погляду.

9.

1) log 5 x 0;
1) х 1
x
2) log 3 3 4;
2) х 4
3) log 3 x 1 0;
3) х 3
4) log 2 (2 x 1) 3;
4) х 4,5
5) log 3 (2 x 3) 1 0;
5) х 3
6) log 5 (2 x x ) 0;
6)
7) log 0,7 (2 x 1) log 0,7 ( x 1).
7) х 2
2
2
х 1

10.

Нехай log 2 x a; a 2 4a 3 0,
log 32 x 4 log 3 x 3
a 1 4; a 2 1.
звідси log 2 x 4, тому х 16;
log 2 x 1, х 0,5. Відповідь :16; 0, 5.
log 5 ( x 1) log 5 ( x 2) log 5 ( x 2)
Пропотенціюємо дану рівність і
одержимо:
log5( x-1)( x-2) = log5( x+2);
x2-4x=0; х=0, х=4.
Враховуючи ОДЗ: х-1>0,
х-2>0,
х+2>0;
хЄ(2; )
Відповідь: 4.

11.

log 3 х 2log 1 x 3 ОДЗ : х. 0
log 3 x
log 3 х 2
3;
1
log 3
3
Відповідь : Х 3.
3
log 3 x 2 log 3 x 3; 3log 3 x 3; x 3.
x
lgx
100 x.
ОДЗ : х. 0
Прологарифмуємо обидві частини рівняння (х 0): lgx lgx lg 100 x
.Одержимо lg x lg x lg 100 lg x; lg 2 x lg x 2 0.
Замінемо : lgx a, тому а 2 а 2 0. а1 2; а 2 1.
Тоді : 1)lgx 2; x 10 2 , x 100.
2)lgx -1 : x 10 -1 , x 0,1.
Відповідь : 100; 0,1.

12.

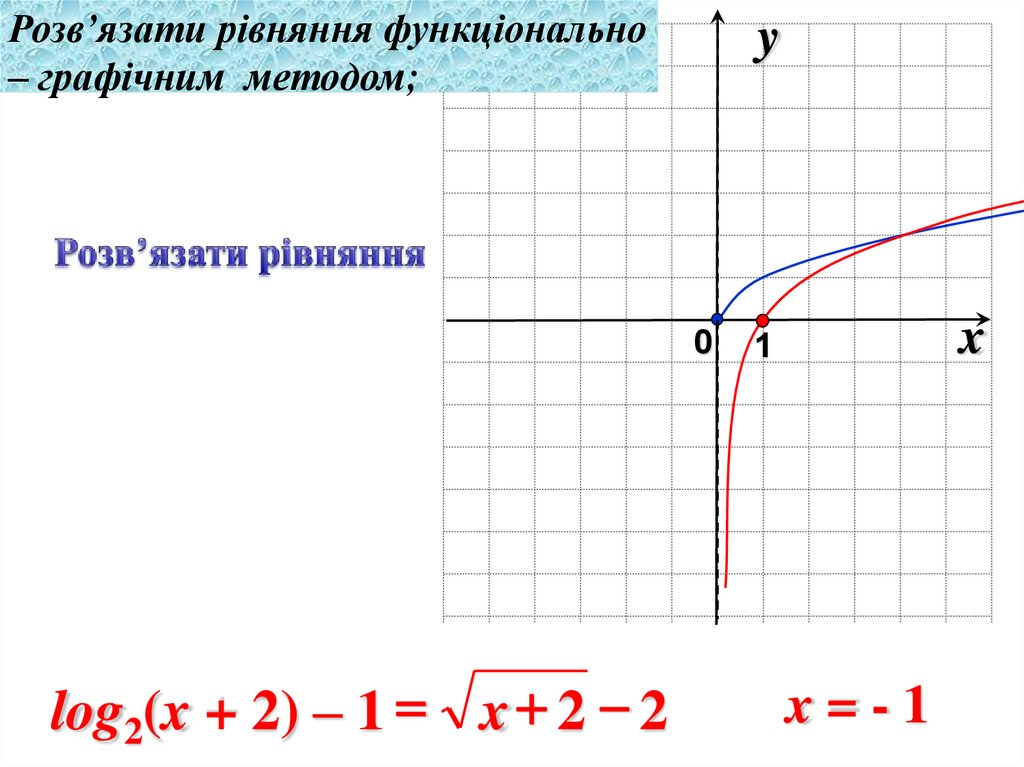
Розв’язати рівняння функціонально
– графічним методом;
y
0
log2(x + 2) – 1 x 2 2
x
1
x=-1

13.

.
y
Подумай!
-0
-1
2
1
Подумай
!
Подумай!
y=1-x
y=lgx
1
-1 0
1
x
Вірно!
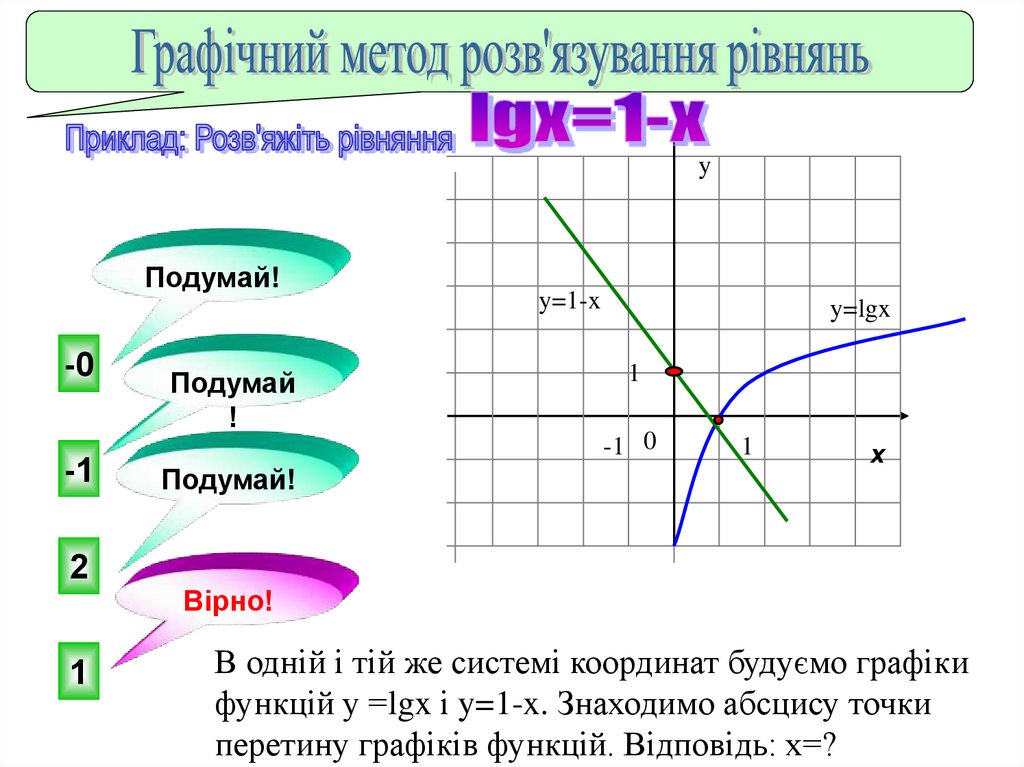
В одній і тій же системі координат будуємо графіки
функцій у =lgx і y=1-x. Знаходимо абсцису точки
перетину графіків функцій. Відповідь: х=?

14.

Розв’язати рівняння: lg3 0,5lg( x 28) lg
Розв’язування :
x 10
lg3 0,5lg( x 28) lg x 10
lg(3 x 28) lg x 10
Враховуючи ОДЗ, дане рівняння рівносильне системі:
x 28 0,
x 10 0,
3 x 28 x 10 ;
x 28,
x 10,
9( x 28) x 10;
x 28,
9 x 252 x 10;
x 28,
x 32,75;
Відповідь: 32,75

15.

Розв’язати рівняння: lg3 0,5lg( x 28) lg
Розв’язування :
x 10
lg3 0,5lg( x 28) lg x 10
lg(3 x 28) lg x 10
Враховуючи ОДЗ, дане рівняння рівносильне системі:
x 28 0,
x 10 0,
3 x 28 x 10 ;
x 28,
x 10,
9( x 28) x 10;
x 28,
9 x 252 x 10;
x 28,
x 32,75;
Відповідь: 32,75

16.

log 3 x 6
2
x 27,
log 3 x 6 2 log 3 x 6 log 3 x 3 x 27
x 27.
Відповідь : 27;27.
2
log ( x) 3 log 2 x 5 0
2
2
О.Д.З. х
<о.
2
log 22 x 6 log 2 x 5 0
Нехай log 2 x t , отже, t 2 6t 5 0,
t 1 5, то log 2 x 5, х 32.
t 2 1, то log 2 x 1, x 2.
Відповідь: не має розв’язків

17.

Розв’язати нерівність:
Розв’язування :
( 4 x 1) 15
2
log 2
x 2
2
( 4 x 1) 15
log1 2
2
4 x 1 0,
4( x 4)
x 5
log
log
0;
2
2 x 2 2
28
log 2
x 2
2
log1 2
28
x 5
28
x 5
0,
4 x 1 0,
4( x 4)( x 5)
log
2 28( x 2 2) log 2 1; _ ò .ê. _ y log 2 t , _ ò î
4 x 1 0,
( x 4)( x 5)
7( x 2 2) 1;
4 x 1 0,
2
2 x 3 x 2 0;
x 1 4,
x ( 1 2 ; 2).
Відповідь: x 1 ; 2).
4
2 x 3 x 2 0,
2
f ( x) 2 x 3x 2
2
Î ÄÇ : x R
Í óëè _ ô öè : x1 1 2 ; x2 2
0

18.

Підсумок уроку
Давайте пригадаємо…
Закінчити речення:
Логарифмом додатного числа в
за основою а називається…
Логарифмічними рівняннями
називаються…
Розв’язати логарифмічне
рівняння – це означає…

19. Домашнє завданння: