Лінійні рівняння, 7 клас

1. Лінійні рівняння

Никитенко Ганна Григорівна, учитель математики СЗШ № 22
Солом’янського району м. Києва
Лінійні рівняння
Сьогодні на уроці:
1. Повторимо, що називається рівнянням та його коренем.
2. Згадаємо, які рівняння є рівносильними.
3. Познайомимося з лінійними рівняннями.
4. Проаналізуємо алгоритм розв'язування лінійних рівнянь.
5. Використаємо алгоритм на практиці.

2. 1. Що називається рівнянням? 2. Що називається коренем рівняння? 3. Що означає розв'язати рівняння? 4. Які рівняння називаються

1
Згадай, ти це знаєш!
1. Що називається рівнянням?
2. Що називається коренем
рівняння?
3. Що означає розв'язати
рівняння?
4. Які рівняння називаються
рівносильними?

3. * Рівняння-це рівність, що містить змінну (невідоме) 5х – 10 = 3 + 19х ліва права частина частина 5х, - 10, 3, 19х – члени

2
Згадай, ти це знаєш!
* Рівняння-це рівність, що містить змінну
(невідоме) 5х – 10 = 3 + 19х
ліва
частина
права
частина
5х, - 10, 3, 19х – члени рівняння
* Розв'язати рівняння означає знайти
його корені або довести, що коренів немає

4.

3
Згадай, ти це знаєш!
Коренем рівняння або розв'язком рівняння
називаємо значення змінної, для якого
рівняння перетворюється в правильну
числову рівність.
Наприклад:
3х=6
Число 2 – корінь рівняння, а число 5 – ні

5.

4
Згадай, ти це знаєш!
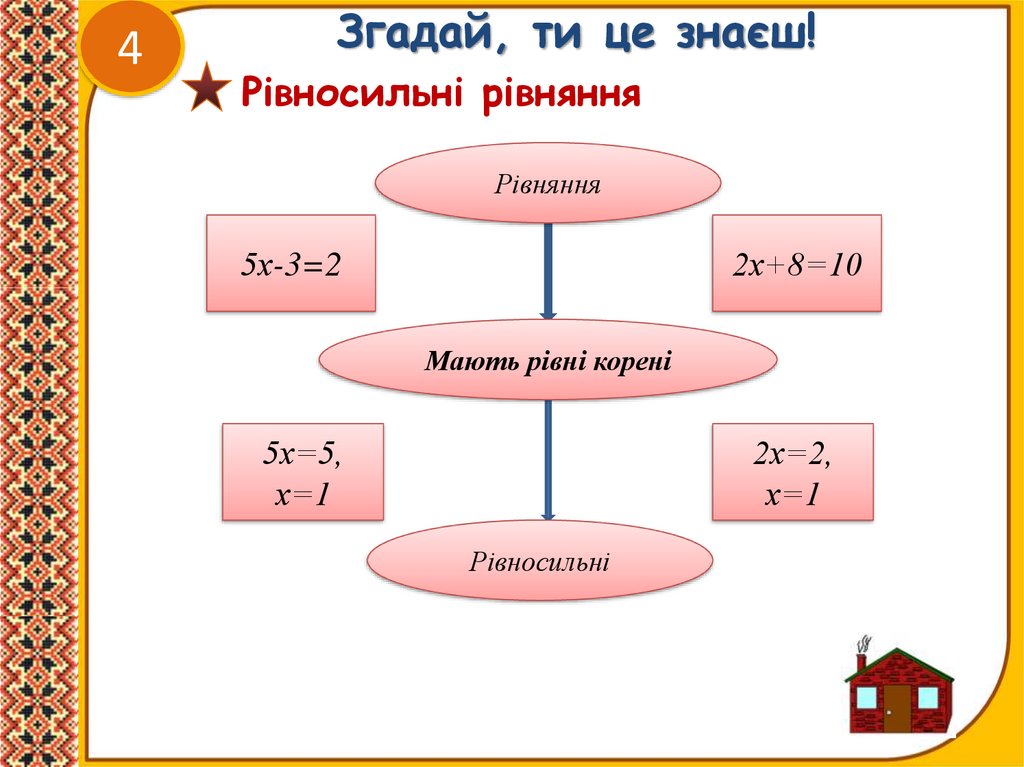
Рівносильні рівняння
Рівняння
5х-3=2
2х+8=10
Мають рівні корені
5х=5,
х=1
2х=2,
х=1
Рівносильні

6.

5
Згадай, ти це знаєш!
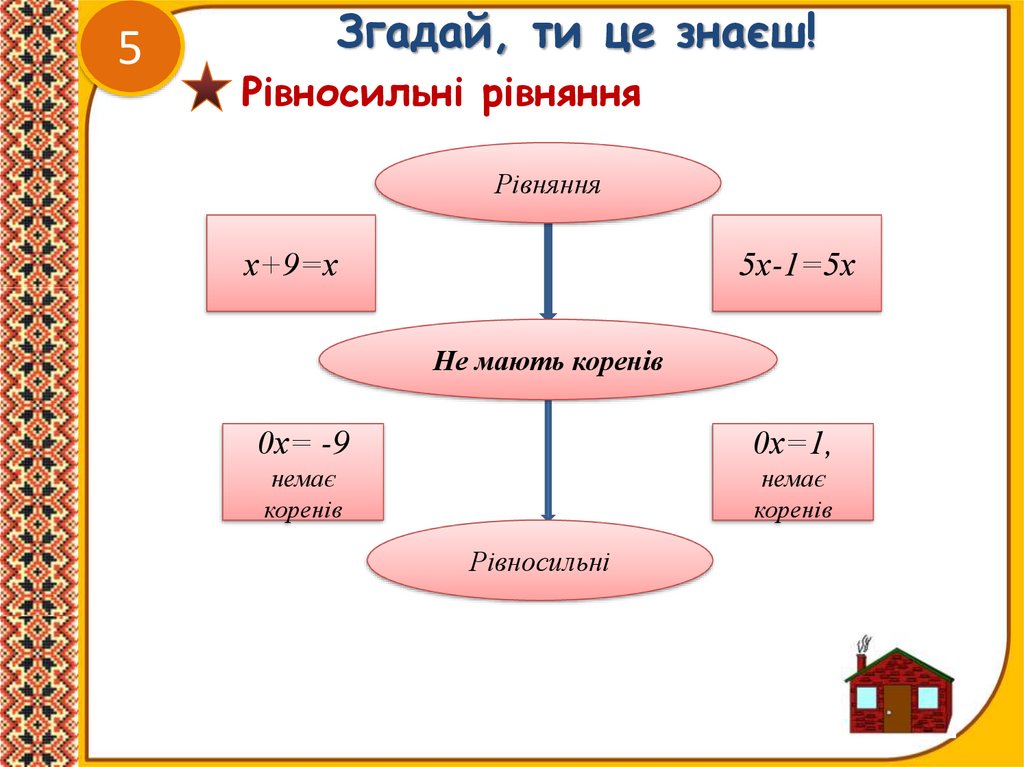
Рівносильні рівняння
Рівняння
х+9=х
5х-1=5х
Не мають коренів
0х= -9
0х=1,
немає
коренів
немає
коренів
Рівносильні

7.

6
Зрозумій, це просто!
Рівняння виду
ax=b,
де a i b деякі відомі числа, коефіцієнти,
х – змінна, це є лінійним рівнянням з
однією змінною.
НАПРИКЛАД:
3х=2;
а=3, b=2
0х=6;
а=0, b=6
0х=0;
а=0, b=0

8.

7
Зрозумій, це просто!
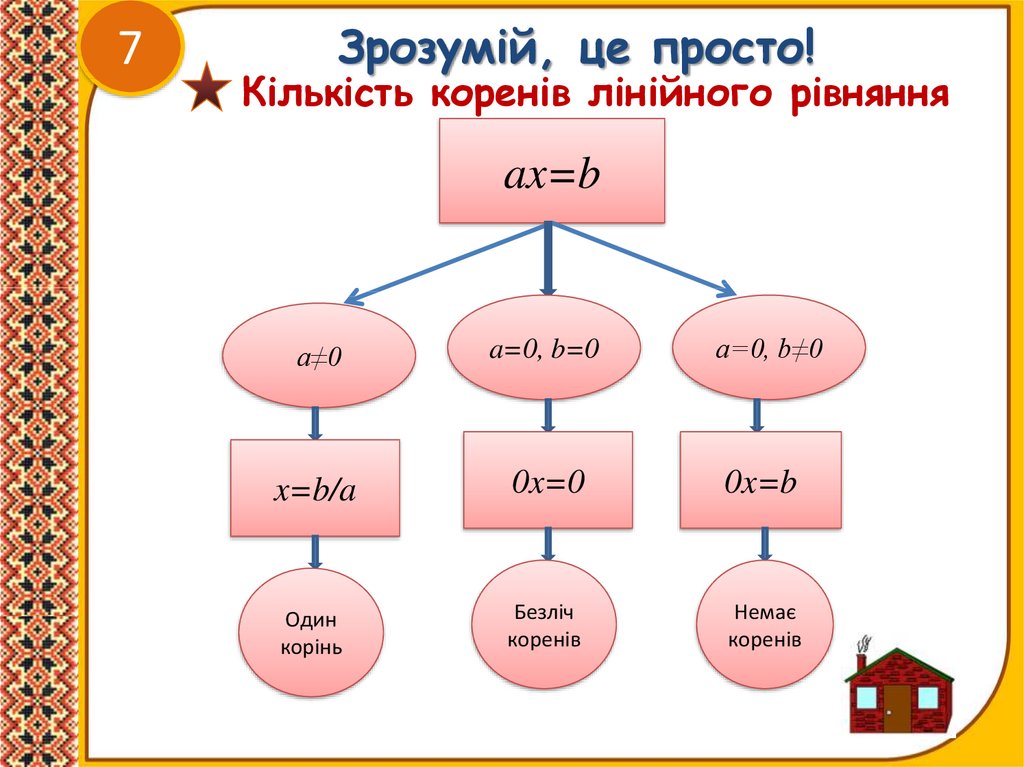
Кількість коренів лінійного рівняння
ax=b
a≠0
a=0, b=0
a=0, b≠0
x=b/a
0x=0
0x=b
Один
корінь
Безліч
коренів
Немає
коренів

9.

y
x
:
8
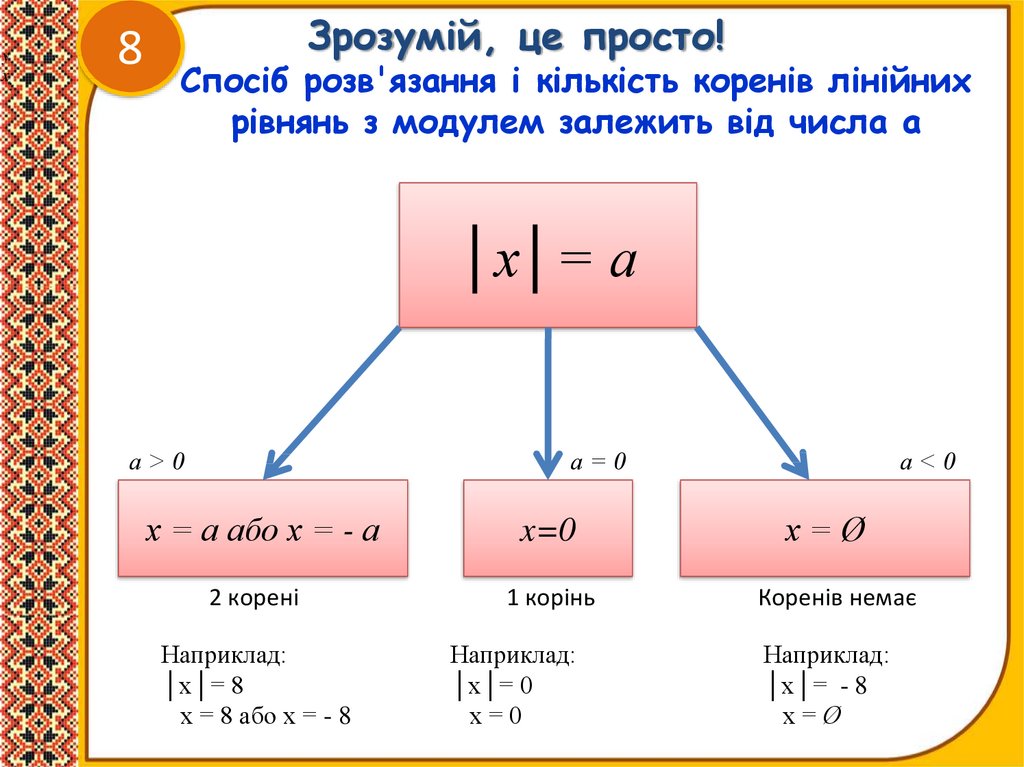
Зрозумій, це просто!
Спосіб розв'язання і кількість коренів лінійних
рівнянь з модулем залежить від числа а
│х│= а
а>0
а=0
х = а або х = - а
2 корені
Наприклад:
│х│= 8
х = 8 або х = - 8
x=0
1 корінь
Наприклад:
│х│= 0
х=0
а<0
х=Ø
Коренів немає
Наприклад:
│х│= - 8
х=Ø

10.

y
x
:
9
Зрозумій, це просто!
Алгоритм розв'язування лінійних рівнянь
Алгоритм дій:
Приклад
Позбутися знаменників.
Помножити обидві частини
рівняння на 30
3(3х-2) - 2(4х+5) = 5х
Розкрити дужки
9х – 6 - 8х – 10 = 5х
Перенести члени рівняння з
невідомими в ліву частину
рівняння, а числа – у праву,
змінивши знаки на протилежні
9х - 8х - 5х = 10 + 6
Звести подібні доданки
- 4 х = 16
Поділити обидві частини рівняння
на – 4
х = 16 : (-4)
х=-4
Записати відповідь
-4

11.

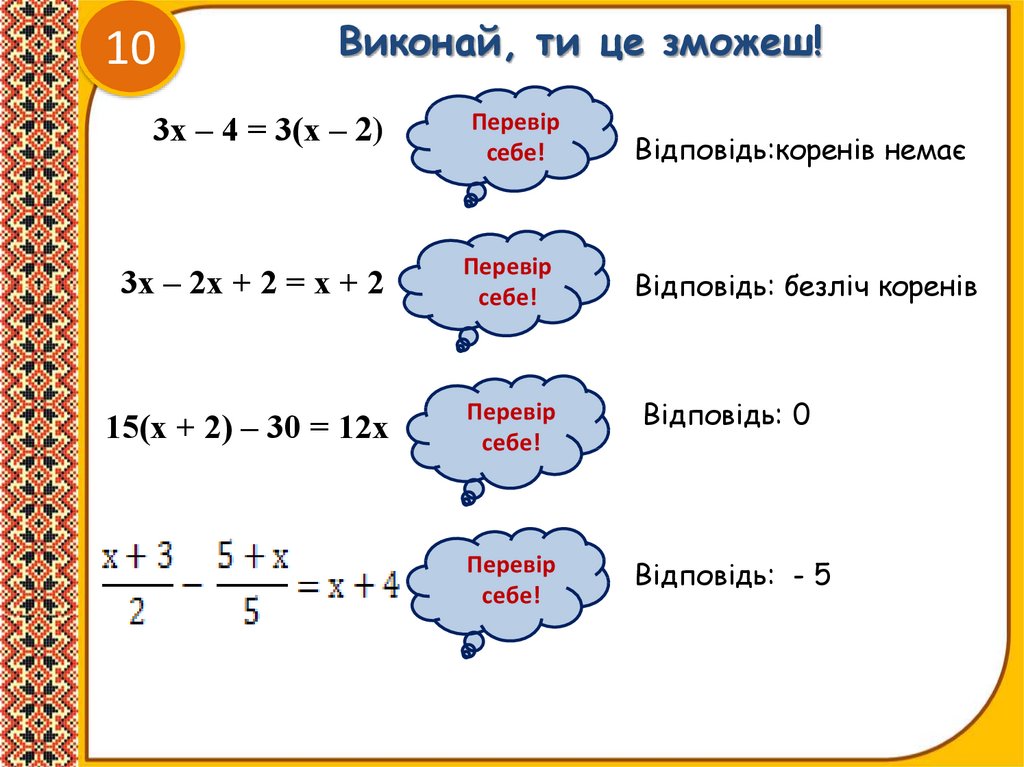
10
Виконай, ти це зможеш!
3х – 4 = 3(х – 2)
Перевір
себе!
Відповідь:коренів немає
3х – 2х + 2 = х + 2
Перевір
себе!
15(х + 2) – 30 = 12х
Перевір
себе!
Відповідь: 0
Перевір
себе!
Відповідь: - 5
Відповідь: безліч коренів

12.

11
Пригадай головне!
1. Яке рівняння називається лінійним?
2. Скільки розв'язків може мати рівняння
1-го степеня з однією змінною?
3. Сформулювати основні властивості
рівнянь.
4. Від чого залежить кількість коренів
лінійного рівняння з модулем?
5. Навести приклад рівняння,
рівносильного даному:
3х – 7 = 10
х–2=х–2
6. Назвати алгоритм розв'язування лінійних
рівнянь.